Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- 2D Graphics »
Sage provides extensive 2D plotting functionality. The underlying rendering is done using the matplotlib Python library.
The following graphics primitives are supported:
The following plotting functions are supported:
The following miscellaneous Graphics functions are included:
Type ? after each primitive in Sage for help and examples.
EXAMPLES: We construct a plot involving several graphics objects:
sage: G = plot(cos, -5, 5, thickness=5, color='green')
sage: P = polygon([[1,2], [5,6], [5,0]], color='red')
sage: G + P # show it
We draw a circle and a curve:
sage: circle((1,1), 1) + plot(x^2, (x,0,5))
Notice that the above circle is not round, because the aspect ratio of the coordinate system is not 1:1. The aspect_ratio option to show allows us to fix this:
sage: show(circle((1,1), 1) + plot(x^2, (x,0,5)), aspect_ratio=1)
With an aspect ratio of 2 the circle is squashed half way down (it looks twice as wide as it does tall):
sage: show(circle((1,1), 1) + plot(x^2, (x,0,5)), aspect_ratio=2)
Use figsize to set the actual aspect ratio of the rendered image (i.e., of the frame). For example, this image is twice as many pixels wide as it is tall:
sage: show(circle((1,1), 1) + plot(x^2, (x,0,5)), figsize=[8,4])
Note that the axes will not cross if the data is not on both sides of both axes, even if it is quite close:
sage: plot(x^3,(x,1,10))
When the labels have quite different orders of magnitude or are very
large, scientific notation (the  notation for powers of ten) is used:
notation for powers of ten) is used:
sage: plot(x^2,(x,480,500)) # no scientific notation
sage: plot(x^2,(x,300,500)) # scientific notation on y-axis
Next we construct the reflection of the above polygon about the
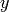 -axis by iterating over the list of first-coordinates of
the first graphic element of
-axis by iterating over the list of first-coordinates of
the first graphic element of 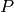 (which is the actual
Polygon; note that
(which is the actual
Polygon; note that 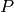 is a Graphics object, which consists
of a single polygon):
is a Graphics object, which consists
of a single polygon):
sage: Q = polygon([(-x,y) for x,y in P[0]], color='blue')
sage: Q # show it
We combine together different graphics objects using “+”:
sage: H = G + P + Q
sage: print H
Graphics object consisting of 3 graphics primitives
sage: type(H)
<class 'sage.plot.plot.Graphics'>
sage: H[1]
Polygon defined by 3 points
sage: list(H[1])
[(1.0, 2.0), (5.0, 6.0), (5.0, 0.0)]
sage: H # show it
We can put text in a graph:
sage: L = [[cos(pi*i/100)^3,sin(pi*i/100)] for i in range(200)]
sage: p = line(L, rgbcolor=(1/4,1/8,3/4))
sage: t = text('A Bulb', (1.5, 0.25))
sage: x = text('x axis', (1.5,-0.2))
sage: y = text('y axis', (0.4,0.9))
sage: g = p+t+x+y
sage: g.show(xmin=-1.5, xmax=2, ymin=-1, ymax=1)
We plot the Riemann zeta function along the critical line and see the first few zeros:
sage: i = CDF.0 # define i this way for maximum speed.
sage: p1 = plot(lambda t: arg(zeta(0.5+t*i)), 1,27,rgbcolor=(0.8,0,0))
sage: p2 = plot(lambda t: abs(zeta(0.5+t*i)), 1,27,color=hue(0.7))
sage: print p1 + p2
Graphics object consisting of 2 graphics primitives
sage: p1 + p2 # display it
Many concentric circles shrinking toward the origin:
sage: show(sum(circle((i,0), i, hue=sin(i/10)) for i in [10,9.9,..,0]), aspect_ratio=1)
Here is a pretty graph:
sage: g = Graphics()
sage: for i in range(60):
... p = polygon([(i*cos(i),i*sin(i)), (0,i), (i,0)],\
... color=hue(i/40+0.4), alpha=0.2)
... g = g + p
...
sage: g.show(dpi=200, axes=False)
Another graph:
sage: x = var('x')
sage: P = plot(sin(x)/x, -4,4, color='blue') + \
... plot(x*cos(x), -4,4, color='red') + \
... plot(tan(x),-4,4, color='green')
...
sage: P.show(ymin=-pi,ymax=pi)
PYX EXAMPLES: These are some examples of plots similar to some of the plots in the PyX (http://pyx.sourceforge.net) documentation:
Symbolline:
sage: y(x) = x*sin(x^2)
sage: v = [(x, y(x)) for x in [-3,-2.95,..,3]]
sage: show(points(v, rgbcolor=(0.2,0.6, 0.1), pointsize=30) + plot(spline(v), -3.1, 3))
Cycliclink:
sage: x = var('x')
sage: g1 = plot(cos(20*x)*exp(-2*x), 0, 1)
sage: g2 = plot(2*exp(-30*x) - exp(-3*x), 0, 1)
sage: show(graphics_array([g1, g2], 2, 1), xmin=0)
Pi Axis: In the PyX manual, the point of this example is to show labeling the X-axis using rational multiples of Pi. Sage currently has no support for controlling how the ticks on the x and y axes are labeled, so this is really a bad example:
sage: g1 = plot(sin(x), 0, 2*pi)
sage: g2 = plot(cos(x), 0, 2*pi, linestyle = "--")
sage: g1 + g2 # show their sum
An illustration of integration:
sage: f(x) = (x-3)*(x-5)*(x-7)+40
sage: P = line([(2,0),(2,f(2))], color='black')
sage: P += line([(8,0),(8,f(8))], color='black')
sage: P += polygon([(2,0),(2,f(2))] + [(x, f(x)) for x in [2,2.1,..,8]] + [(8,0),(2,0)], rgbcolor=(0.8,0.8,0.8))
sage: P += text("$\\int_{a}^b f(x) dx$", (5, 20), fontsize=16, color='black')
sage: P += plot(f, (1, 8.5), thickness=3)
sage: P # show the result
NUMERICAL PLOTTING:
Sage includes Matplotlib, which provides 2D plotting with an interface that is a likely very familiar to people doing numerical computation. For example,
sage: from pylab import *
sage: t = arange(0.0, 2.0, 0.01)
sage: s = sin(2*pi*t)
sage: P = plot(t, s, linewidth=1.0)
sage: xl = xlabel('time (s)')
sage: yl = ylabel('voltage (mV)')
sage: t = title('About as simple as it gets, folks')
sage: grid(True)
sage: savefig(os.path.join(SAGE_TMP, 'sage.png'))
We test that imshow works as well, verifying that Trac ticket 2900 is fixed in Matplotlib.
sage: imshow([[(0,0,0)]])
<matplotlib.image.AxesImage object at ...>
sage: savefig(os.path.join(SAGE_TMP, 'foo.png'))
Since the above overwrites many Sage plotting functions, we reset the state of Sage, so that the examples below work!
sage: reset()
See http://matplotlib.sourceforge.net for complete documentation about how to use Matplotlib.
TESTS: We test dumping and loading a plot.
sage: p = plot(sin(x), (x, 0,2*pi))
sage: Q = loads(dumps(p))
Verify that a clean sage startup does not import matplotlib:
sage: os.system("sage -c \"if 'matplotlib' in sys.modules: sys.exit(1)\"")
0
AUTHORS:
Bases: sage.structure.sage_object.SageObject
The Graphics object is an empty list of graphics objects It is useful to use this object when initializing a for loop where different graphics object will be added to the empty object.
EXAMPLES:
sage: G = Graphics(); print G
Graphics object consisting of 0 graphics primitives
sage: c = circle((1,1), 1,aspect_ratio=1)
sage: G+=c; print G
Graphics object consisting of 1 graphics primitive
Here we make a graphic of embedded isosceles triangles, coloring each one with a different color as we go:
sage: h=10; c=0.4; p=0.5;
sage: G = Graphics()
sage: for x in srange(1,h+1):
... l = [[0,x*sqrt(3)],[-x/2,-x*sqrt(3)/2],[x/2,-x*sqrt(3)/2],[0,x*sqrt(3)]]
... G+=line(l,color=hue(c + p*(x/h)))
sage: G.show(figsize=[5,5])
TESTS:
From trac #4604, ensure Graphics can handle 3d objects:
sage: g = Graphics()
sage: g += sphere((1, 1, 1), 2)
sage: g.show()
Get the current aspect ratio.
OUTPUT: either None if the aspect ratio hasn’t been set or a positive float
EXAMPLES:
sage: P = circle((1,1), 1)
sage: P.aspect_ratio() is None
True
sage: P.set_aspect_ratio(2)
sage: P.aspect_ratio()
2.0
Set whether or not the  and
and 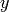 axes are shown
by default.
axes are shown
by default.
INPUT:
If called with no input, return the current axes setting.
EXAMPLES:
sage: L = line([(1,2), (3,-4), (2, 5), (1,2)])
By default the axes are displayed.
sage: L.axes()
True
But we turn them off, and verify that they are off
sage: L.axes(False)
sage: L.axes()
False
Displaying L now shows a triangle but no axes.
sage: L
Set the axes color.
If called with no input, return the current axes_color setting.
INPUT:
EXAMPLES: We create a line, which has like everything a default axes color of black.
sage: L = line([(1,2), (3,-4), (2, 5), (1,2)])
sage: L.axes_color()
(0, 0, 0)
We change the axes color to red and verify the change.
sage: L.axes_color((1,0,0))
sage: L.axes_color()
(1.0, 0.0, 0.0)
When we display the plot, we’ll see a blue triangle and bright red axes.
sage: L
Set the color of the axes labels.
The axes labels are placed at the edge of the x and y axes, and are not on by default (use the axes_labels command to set them; see the example below). This function just changes their color.
INPUT:
If called with no input, return the current axes_label_color setting.
EXAMPLES: We create a plot, which by default has axes label color black.
sage: p = plot(sin, (-1,1))
sage: p.axes_label_color()
(0, 0, 0)
We change the labels to be red, and confirm this:
sage: p.axes_label_color((1,0,0))
sage: p.axes_label_color()
(1.0, 0.0, 0.0)
We set labels, since otherwise we won’t see anything.
sage: p.axes_labels(['$x$ axis', '$y$ axis'])
In the plot below, notice that the labels are red:
sage: p
Set the axes labels.
INPUT:
OUTPUT: a 2-tuple of strings
If l is None, returns the current axes_labels, which is itself by default None. The default labels are both empty.
EXAMPLES: We create a plot and put x and y axes labels on it.
sage: p = plot(sin(x), (x, 0, 10))
sage: p.axes_labels(['$x$','$y$'])
sage: p.axes_labels()
('$x$', '$y$')
Now when you plot p, you see x and y axes labels:
sage: p
Notice that some may prefer axes labels which are not typeset:
sage: plot(sin(x), (x, 0, 10), axes_labels=['x','y'])
Set the ranges of the  and
and 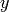 axes.
axes.
INPUT:
EXAMPLES:
sage: L = line([(1,2), (3,-4), (2, 5), (1,2)])
sage: L.set_axes_range(-1, 20, 0, 2)
sage: d = L.get_axes_range()
sage: d['xmin'], d['xmax'], d['ymin'], d['ymax']
(-1.0, 20.0, 0.0, 2.0)
Set the axes width. Use this to draw a plot with really fat or really thin axes.
INPUT:
If called with no input, return the current axes_width setting.
EXAMPLE: We create a plot, see the default axes width (with funny Python float rounding), then reset the width to 10 (very fat).
sage: p = plot(cos, (-3,3))
sage: p.axes_width()
0.80000000000000004
sage: p.axes_width(10)
sage: p.axes_width()
10.0
Finally we plot the result, which is a graph with very fat axes.
sage: p
Set the font size of axes labels and tick marks.
INPUT:
If called with no input, return the current fontsize.
EXAMPLES:
sage: L = line([(1,2), (3,-4), (2, 5), (1,2)])
sage: L.fontsize()
10
sage: L.fontsize(20)
sage: L.fontsize()
20
All the numbers on the axes will be very large in this plot:
sage: L
Returns a dictionary of the range of the axes for this graphics object. This is fall back to the ranges in get_minmax_data() for any value which the user has not explicitly set.
Warning
Changing the dictionary returned by this function does not change the axes range for this object. To do that, use the set_axes_range() method.
EXAMPLES:
sage: L = line([(1,2), (3,-4), (2, 5), (1,2)])
sage: list(sorted(L.get_axes_range().items()))
[('xmax', 3.0), ('xmin', 1.0), ('ymax', 5.0), ('ymin', -4.0)]
sage: L.set_axes_range(xmin=-1)
sage: list(sorted(L.get_axes_range().items()))
[('xmax', 3.0), ('xmin', -1.0), ('ymax', 5.0), ('ymin', -4.0)]
Return a dictionary whose keys give the xmin, xmax, ymin, and ymax data for this graphic.
Warning
The returned dictionary is mutable, but changing it does not change the xmin/xmax/ymin/ymax data. The minmax data is a function of the primitives which make up this Graphics object. To change the range of the axes, call methods xmin(), xmax(), ymin(), ymax(), or set_axes_range().
EXAMPLES:
sage: g = line([(-1,1), (3,2)])
sage: list(sorted(g.get_minmax_data().items()))
[('xmax', 3.0), ('xmin', -1.0), ('ymax', 2.0), ('ymin', 1.0)]
Note that changing ymax doesn’t change the output of get_minmax_data:
sage: g.ymax(10)
sage: list(sorted(g.get_minmax_data().items()))
[('xmax', 3.0), ('xmin', -1.0), ('ymax', 2.0), ('ymin', 1.0)]
Return a matplotlib figure object representing the graphic
EXAMPLES:
sage: c = circle((1,1),1)
sage: print c.matplotlib()
Figure(480x296.656)
To obtain the first matplotlib axes object inside of the figure, you can do something like the following.
sage: p=plot(sin(x), (x, -2*pi, 2*pi))
sage: figure=p.matplotlib()
sage: axes=figure.axes[0]
For input parameters, see the documentation for the show() method (this function accepts all except the transparent argument).
Draw a 2d plot this graphics object, which just returns this object since this is already a 2d graphics object.
EXAMPLES:
sage: S = circle((0,0), 2)
sage: S.plot() is S
True
Returns an embedding of this 2D plot into the xy-plane of 3D space, as a 3D plot object. An optional parameter z can be given to specify the z-coordinate.
EXAMPLES:
sage: sum([plot(z*sin(x), 0, 10).plot3d(z) for z in range(6)]) #long
Save the graphics to an image file of type: PNG, PS, EPS, SVG, SOBJ, depending on the file extension you give the filename. Extension types can be: .png, .ps, .eps, .svg, and .sobj (for a Sage object you can load later).
EXAMPLES:
sage: c = circle((1,1),1,color='red')
sage: filename=os.path.join(SAGE_TMP, 'test.png')
sage: c.save(filename, xmin=-1,xmax=3,ymin=-1,ymax=3)
To correct the aspect ratio of certain graphics, you can set the aspect_ratio to 1:
sage: c.save(filename, aspect_ratio=1, xmin=-1, xmax=3, ymin=-1, ymax=3)
You could also just make the dimensions of the picture square using figsize:
sage: c.save(filename, figsize=[5,5], xmin=-1, xmax=3, ymin=-1, ymax=3)
sage: point((-1,1),pointsize=30, color='red')
By default, the figure grows to include all of the graphics and text, so the final image may not be exactly the figure size you specified.
Set the aspect ratio.
INPUT:
EXAMPLES: We create a plot of a circle, and it doesn’t look quite round:
sage: P = circle((1,1), 1); P
So we set the aspect ratio and now it is round:
sage: P.set_aspect_ratio(1)
sage: P
Note that the aspect ratio is inherited upon addition (which takes the max of aspect ratios of objects whose aspect ratio has been set):
sage: P + circle((0,0), 0.5) # still square
In the following example, both plots produce a circle that looks twice as wide as tall:
sage: Q = circle((0,0), 0.5); Q.set_aspect_ratio(2)
sage: P + Q
sage: Q + P
Set the ranges of the  and
and 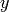 axes.
axes.
INPUT:
EXAMPLES:
sage: L = line([(1,2), (3,-4), (2, 5), (1,2)])
sage: L.set_axes_range(-1, 20, 0, 2)
sage: d = L.get_axes_range()
sage: d['xmin'], d['xmax'], d['ymin'], d['ymax']
(-1.0, 20.0, 0.0, 2.0)
Show this graphics image with the default image viewer.
OPTIONAL INPUT:
filename - (default: None) string
dpi - dots per inch
figsize - [width, height]
aspect_ratio - the perceived width divided by the perceived height. If the aspect ratio is set to 1, circles will look round. If it is set to 2 they will look twice as wide as they are tall. This is the aspect_ratio of the image, not of the frame that contains it. If you want to set the aspect ratio of the frame, use figsize.
axes - (default: True)
axes_labels - (default: None) list (or tuple) of two strings; the first is used as the label for the horizontal axis, and the second for the vertical axis.
fontsize - (default: current setting – 10) positive integer; used for axes labels; if you make this very large, you may have to increase figsize to see all labels.
frame - (default: False) draw a frame around the image
gridlines - (default: None) can be any of the following:
gridlinesstyle, hgridlinesstyle, vgridlinesstyle - (default: None) a dictionary of MATPLOTLIB options for the rendering of the grid lines, the horizontal grid lines or the vertical grid lines, respectively.
to the produced file is returned.
transparent - (default: False) If True, make the background transparent.
axes_pad - (default: 0.02) The percentage of the axis range that is added to each end of each axis. This helps avoid problems like clipping lines because of line-width, etc. To get axes that are exactly the specified limits, set axes_pad to zero.
EXAMPLES:
sage: c = circle((1,1), 1, color='red')
sage: c.show(xmin=-1, xmax=3, ymin=-1, ymax=3)
To correct the aspect ratio of certain graphics, you can set the aspect_ratio to 1
sage: c.show(aspect_ratio=1, xmin=-1, xmax=3, ymin=-1, ymax=3)
You could also just make the dimensions of the picture square using figsize
sage: c.show(figsize=[5,5], xmin=-1, xmax=3, ymin=-1, ymax=3)
You can turn off the drawing of the axes:
sage: show(plot(sin,-4,4), axes=False)
You can also label the axes. Putting something in dollar signs formats it as a mathematical expression:
sage: show(plot(sin,-4,4), axes_labels=('$x$','$y$'))
You can turn on the drawing of a frame around the plots:
sage: show(plot(sin,-4,4), frame=True)
You can make the background transparent:
sage: plot(sin(x), (x, -4, 4), transparent=True)
Add grid lines at the major ticks of the axes.
sage: c = circle((0,0), 1)
sage: c.show(gridlines=True)
sage: c.show(gridlines="automatic")
sage: c.show(gridlines="major")
Add grid lines at the major and minor ticks of the axes.
sage: u,v = var('u v')
sage: f = exp(-(u^2+v^2))
sage: p = plot_vector_field(f.gradient(), (u,-2,2), (v,-2,2))
sage: p.show(gridlines="minor")
Add only horizontal or vertical grid lines.
sage: p = plot(sin,-10,20)
sage: p.show(gridlines=[None, "automatic"])
sage: p.show(gridlines=["minor", False])
Add grid lines at specific positions (using lists/tuples).
sage: x, y = var('x, y')
sage: p = implicit_plot((y^2-x^2)*(x-1)*(2*x-3)-4*(x^2+y^2-2*x)^2, ... (x,-2,2), (y,-2,2), plot_points=1000)
sage: p.show(gridlines=[[1,0],[-1,0,1]])
Add grid lines at specific positions (using iterators).
sage: def maple_leaf(t):
... return (100/(100+(t-pi/2)^8))*(2-sin(7*t)-cos(30*t)/2)
sage: p = polar_plot(maple_leaf, -pi/4, 3*pi/2, color="red",plot_points=1000) #long
sage: p.show(gridlines=( [-3,-2.75,..,3], xrange(-1,5,2) )) #long
Add grid lines at specific positions (using functions).
sage: y = x^5 + 4*x^4 - 10*x^3 - 40*x^2 + 9*x + 36
sage: p = plot(y, -4.1, 1.1)
sage: xlines = lambda a,b: [z for z,m in y.roots()]
sage: p.show(gridlines=[xlines, [0]], frame=True, axes=False)
Change the style of all the grid lines.
sage: b = bar_chart([-3,5,-6,11], color='red')
sage: b.show(gridlines=([-1,-0.5,..,4],True), ... gridlinesstyle=dict(color="blue", linestyle=":"))
Change the style of the horizontal or vertical grid lines separately.
sage: p = polar_plot(2 + 2*cos(x), 0, 2*pi, color=hue(0.3))
sage: p.show(gridlines=True, ... hgridlinesstyle=dict(color="orange", linewidth=1.0), ... vgridlinesstyle=dict(color="blue", linestyle=":"))
Change the style of each grid line individually.
sage: x, y = var('x, y')
sage: p = implicit_plot((y^2-x^2)*(x-1)*(2*x-3)-4*(x^2+y^2-2*x)^2, ... (x,-2,2), (y,-2,2), plot_points=1000)
sage: p.show(gridlines=(
... [
... (1,{"color":"red","linestyle":":"}),
... (0,{"color":"blue","linestyle":"--"})
... ],
... [
... (-1,{"color":"red","linestyle":":"}),
... (0,{"color":"blue","linestyle":"--"}),
... (1,{"color":"red","linestyle":":"}),
... ]
... ),
... gridlinesstyle=dict(marker='x',color="black"))
Grid lines can be added to contour plots.
sage: f = sin(x^2 + y^2)*cos(x)*sin(y)
sage: c = contour_plot(f, (x, -4, 4), (y, -4, 4), plot_points=100)
sage: c.show(gridlines=True, gridlinesstyle={'linestyle':':','linewidth':1, 'color':'red'})
Grid lines can be added to matrix plots.
sage: M = MatrixSpace(QQ,10).random_element()
sage: matrix_plot(M).show(gridlines=True)
By default, Sage increases the horizontal and vertical axes limits by a certain percentage in all directions. This is controlled by the axes_pad parameter. Increasing the range of the axes helps avoid problems with lines and dots being clipped because the linewidth extends beyond the axes. To get axes limits that are exactly what is specified, set axes_pad to zero. Compare the following two examples
sage: plot(sin(x), (x, -pi, pi),thickness=2)+point((pi, -1), pointsize=15)
sage: plot(sin(x), (x, -pi, pi),thickness=2,axes_pad=0)+point((pi, -1), pointsize=15)
Set the color of the axes tick labels.
INPUT:
If called with no input, return the current tick_label_color setting.
EXAMPLES:
sage: p = plot(cos, (-3,3))
sage: p.tick_label_color()
(0, 0, 0)
sage: p.tick_label_color((1,0,0))
sage: p.tick_label_color()
(1.0, 0.0, 0.0)
sage: p
EXAMPLES:
sage: g = line([(-1,1), (3,2)])
sage: g.xmax()
3.0
sage: g.xmax(10)
sage: g.xmax()
10.0
EXAMPLES:
sage: g = line([(-1,1), (3,2)])
sage: g.xmin()
-1.0
sage: g.xmin(-3)
sage: g.xmin()
-3.0
EXAMPLES:
sage: g = line([(-1,1), (3,2)])
sage: g.ymax()
2.0
sage: g.ymax(10)
sage: g.ymax()
10.0
EXAMPLES:
sage: g = line([(-1,1), (3,2)])
sage: g.ymin()
1.0
sage: g.ymin(-3)
sage: g.ymin()
-3.0
Bases: sage.structure.sage_object.SageObject
GraphicsArray takes a (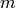 x
x  ) list of lists of
graphics objects and plots them all on one canvas.
) list of lists of
graphics objects and plots them all on one canvas.
Show this graphics array using the default viewer.
OPTIONAL INPUT:
EXAMPLES: This draws a graphics array with four trig plots and no axes in any of the plots.
sage: G = graphics_array([[plot(sin), plot(cos)], [plot(tan), plot(sec)]])
sage: G.show(axes=False)
This matplotlib formatter selectively omits some tick values and passes the rest on to a specified formatter.
EXAMPLES:
This example is almost straight from a matplotlib example.
sage: from sage.plot.plot import SelectiveFormatter
sage: import matplotlib.pyplot as plt
sage: import numpy
sage: fig=plt.figure()
sage: ax=fig.add_subplot(111)
sage: t = numpy.arange(0.0, 2.0, 0.01)
sage: s = numpy.sin(2*numpy.pi*t)
sage: line=ax.plot(t, s)
sage: formatter=SelectiveFormatter(ax.xaxis.get_major_formatter(),skip_values=[0,1])
sage: ax.xaxis.set_major_formatter(formatter)
sage: fig.savefig(os.path.join(SAGE_TMP, 'test.png'))
The adaptive refinement algorithm for plotting a function f. See the docstring for plot for a description of the algorithm.
INPUT:
OUTPUT:
TESTS:
sage: from sage.plot.plot import adaptive_refinement
sage: adaptive_refinement(sin, (0,0), (pi,0), adaptive_tolerance=0.01, adaptive_recursion=0)
[]
sage: adaptive_refinement(sin, (0,0), (pi,0), adaptive_tolerance=0.01)
[(0.125*pi, 0.38268343236508978), (0.1875*pi, 0.55557023301960218), (0.25*pi, 0.70710678118654746), (0.3125*pi, 0.83146961230254524), (0.375*pi, 0.92387953251128674), (0.4375*pi, 0.98078528040323043), (0.5*pi, 1.0), (0.5625*pi, 0.98078528040323043), (0.625*pi, 0.92387953251128674), (0.6875*pi, 0.83146961230254546), (0.75*pi, 0.70710678118654757), (0.8125*pi, 0.55557023301960218), (0.875*pi, 0.38268343236508989)]
This shows that lowering adaptive_tolerance and raising adaptive_recursion both increase the number of subdivision points, though which one creates more points is heavily dependent upon the function being plotted.
sage: x = var('x')
sage: f(x) = sin(1/x)
sage: n1 = len(adaptive_refinement(f, (0,0), (pi,0), adaptive_tolerance=0.01)); n1
15
sage: n2 = len(adaptive_refinement(f, (0,0), (pi,0), adaptive_recursion=10, adaptive_tolerance=0.01)); n2
79
sage: n3 = len(adaptive_refinement(f, (0,0), (pi,0), adaptive_tolerance=0.001)); n3
26
Adjust the figsize in case the user also specifies an aspect ratio.
INPUTS: figsize - a sequence of two positive real numbers aspect_ratio - a positive real number xmin, xmax, ymin, ymax - real numbers
EXAMPLES: This function is used mainly internally by plotting code so we explicitly import it:
sage: from sage.plot.plot import adjust_figsize_for_aspect_ratio
This returns (5,5), since the requested aspect ratio is 1 and the x and y ranges are the same, so that’s the right size rendered image to produce a 1:1 ratio internally. 5 is used instead of 3 since the image size is always adjusted to the larger of the figsize dimensions.
sage: adjust_figsize_for_aspect_ratio([3,5], 1, 0, 2, 0, 2)
(5, 5)
Here we give a scalar figsize, which is automatically converted to the figsize (figsize, figsize/golden_ratio).
sage: adjust_figsize_for_aspect_ratio(3, 1, 0, 2, 0, 2)
(3, 3)
Here we omit the aspect ratio so the figsize is just returned.
sage: adjust_figsize_for_aspect_ratio([5,6], None, 0, 2, 0, 2)
[5, 6]
Here we have an aspect ratio of 2, and since the x and y ranges are the same the returned figsize is twice as wide as tall:
sage: adjust_figsize_for_aspect_ratio([3,5], 2, 0, 2, 0, 2)
(5, 5/2)
Here the x range is rather large, so to get an aspect ratio where circles look twice as wide as they are tall, we have to shrink the y size of the image.
sage: adjust_figsize_for_aspect_ratio([3,5], 2, 0, 10, 0, 2)
(5, 1/2)
Calculate plot points for a function f in the interval xrange. The adaptive refinement algorithm is also automatically invoked with a relative adaptive tolerance of adaptive_tolerance; see below.
INPUT:
OUTPUT:
TESTS:
sage: from sage.plot.plot import generate_plot_points
sage: generate_plot_points(sin, (0, pi), plot_points=2, adaptive_recursion=0)
[(0.0, 0.0), (3.1415926535897931, 1.2246...e-16)]
sage: from sage.plot.plot import generate_plot_points
sage: generate_plot_points(lambda x: x^2, (0, 6), plot_points=2, adaptive_recursion=0, initial_points = [1,2,3])
[(0.0, 0.0), (1.0, 1.0), (2.0, 4.0), (3.0, 9.0), (6.0, 36.0)]
sage: generate_plot_points(sin(x).function(x), (-pi, pi), randomize=False)
[(-3.1415926535897931, -1.2246...e-16), (-2.748893571891069,
-0.3826834323650898...), (-2.3561944901923448, -0.707106781186547...),
(-2.1598449493429825, -0.831469612302545...), (-1.9634954084936207,
-0.92387953251128674), (-1.7671458676442586, -0.98078528040323043),
(-1.5707963267948966, -1.0), (-1.3744467859455345,
-0.98078528040323043), (-1.1780972450961724, -0.92387953251128674),
(-0.98174770424681035, -0.831469612302545...), (-0.78539816339744828,
-0.707106781186547...), (-0.39269908169872414, -0.38268343236508978),
(0.0, 0.0), (0.39269908169872414, 0.38268343236508978),
(0.78539816339744828, 0.707106781186547...), (0.98174770424681035,
0.831469612302545...), (1.1780972450961724, 0.92387953251128674),
(1.3744467859455345, 0.98078528040323043), (1.5707963267948966, 1.0),
(1.7671458676442586, 0.98078528040323043), (1.9634954084936207,
0.92387953251128674), (2.1598449493429825, 0.831469612302545...),
(2.3561944901923448, 0.707106781186547...), (2.748893571891069,
0.3826834323650898...), (3.1415926535897931, 1.2246...e-16)]
This shows that lowering adaptive_tolerance and raising adaptive_recursion both increase the number of subdivision points. (Note that which creates more points is heavily dependent on the particular function plotted.)
sage: x = var('x')
sage: f(x) = sin(1/x)
sage: [len(generate_plot_points(f, (-pi, pi), plot_points=16, adaptive_tolerance=i, randomize=False)) for i in [0.01, 0.001, 0.0001]]
[97, 161, 275]
sage: [len(generate_plot_points(f, (-pi, pi), plot_points=16, adaptive_recursion=i, randomize=False)) for i in [5, 10, 15]]
[97, 499, 2681]
graphics_array take a list of lists (or tuples) of graphics objects and plots them all on one canvas (single plot).
INPUT:
EXAMPLE: Make some plots of 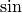 functions:
functions:
sage: f(x) = sin(x)
sage: g(x) = sin(2*x)
sage: h(x) = sin(4*x)
sage: p1 = plot(f,(-2*pi,2*pi),color=hue(0.5))
sage: p2 = plot(g,(-2*pi,2*pi),color=hue(0.9))
sage: p3 = parametric_plot((f,g),(0,2*pi),color=hue(0.6))
sage: p4 = parametric_plot((f,h),(0,2*pi),color=hue(1.0))
Now make a graphics array out of the plots; then you can type either: ga.show() or ga.save().
sage: graphics_array(((p1,p2),(p3,p4)))
Here we give only one row:
sage: p1 = plot(sin,(-4,4))
sage: p2 = plot(cos,(-4,4))
sage: g = graphics_array([p1, p2]); print g
Graphics Array of size 1 x 2
sage: g.show()
Return True if  is a Graphics object.
is a Graphics object.
EXAMPLES:
sage: from sage.plot.plot import is_Graphics
sage: is_Graphics(1)
False
sage: is_Graphics(disk((0.0, 0.0), 1, (0, pi/2)))
True
list_plot takes a single list of data, in which case it forms
a list of tuples 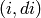 where
where  goes from 0 to
goes from 0 to
 and
and 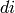 is the
is the 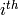 data value, and puts points
at those tuple values.
data value, and puts points
at those tuple values.
list_plot also takes a list of tuples 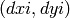 where
where 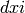 is the
is the  data representing the
data representing the  -value, and
-value, and 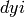 is the
is the
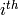
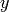 -value. If plotjoined=True , then a line spanning
all the data is drawn instead.
-value. If plotjoined=True , then a line spanning
all the data is drawn instead.
EXAMPLES:
sage: list_plot([i^2 for i in range(5)])
Here are a bunch of random red points:
sage: r = [(random(),random()) for _ in range(20)]
sage: list_plot(r,color='red')
This gives all the random points joined in a purple line:
sage: list_plot(r, plotjoined=True, color='purple')
If you have separate lists of  values and
values and 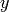 values which you
want to plot against each other, use the zip command to make a
single list whose entries are pairs of
values which you
want to plot against each other, use the zip command to make a
single list whose entries are pairs of 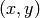 values, and feed
the result into list_plot:
values, and feed
the result into list_plot:
sage: x_coords = [cos(t)^3 for t in srange(0, 2*pi, 0.02)]
sage: y_coords = [sin(t)^3 for t in srange(0, 2*pi, 0.02)]
sage: list_plot(zip(x_coords, y_coords))
If instead you try to pass the two lists as separate arguments, you will get an error message:
sage: list_plot(x_coords, y_coords)
...
TypeError: The second argument 'plotjoined' should be boolean (True or False). If you meant to plot two lists 'x' and 'y' against each other, use 'list_plot(zip(x,y))'.
TESTS: We check to see that the x/y min/max data are set correctly.
sage: d = list_plot([(100,100), (120, 120)]).get_minmax_data()
sage: d['xmin']
100.0
sage: d['ymin']
100.0
Returns the minimums and maximums of xdata and ydata.
If dict is False, then minmax_data returns the tuple (xmin, xmax, ymin, ymax); otherwise, it returns a dictionary whose keys are ‘xmin’, ‘xmax’, ‘ymin’, and ‘ymax’ and whose values are the corresponding values.
EXAMPLES:
sage: from sage.plot.plot import minmax_data
sage: minmax_data([], [])
(-1, 1, -1, 1)
sage: minmax_data([-1, 2], [4, -3])
(-1, 2, -3, 4)
sage: d = minmax_data([-1, 2], [4, -3], dict=True)
sage: list(sorted(d.items()))
[('xmax', 2), ('xmin', -1), ('ymax', 4), ('ymin', -3)]
parametric_plot takes two or three functions as a
list or a tuple and makes a plot with the first function giving the
 coordinates, the second function giving the
coordinates, the second function giving the 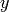 coordinates, and the third function (if present) giving the
coordinates, and the third function (if present) giving the
 coordinates.
coordinates.
In the 2d case, parametric_plot is equivalent to the plot command with the option parametric=True. In the 3d case, parametric_plot is equivalent to parametric_plot3d. See each of these functions for more help and examples.
INPUT:
EXAMPLES: We draw some 2d parametric plots:
sage: t = var('t')
sage: parametric_plot( (sin(t), sin(2*t)), (t, 0, 2*pi), color=hue(0.6) )
sage: parametric_plot((1, t), (t, 0, 4))
Note that in parametric_plot, there is only fill or no fill.
sage: parametric_plot((t, t^2), (t, -4, 4), fill = True)
A filled Hypotrochoid:
sage: parametric_plot([cos(x) + 2 * cos(x/4), sin(x) - 2 * sin(x/4)], (x,0, 8*pi), fill = True)
sage: parametric_plot( (5*cos(x), 5*sin(x), x), (x,-12, 12), plot_points=150, color="red")
sage: y=var('y')
sage: parametric_plot( (5*cos(x), x*y, cos(x*y)), (x, -4,4), (y,-4,4))
sage: t=var('t')
sage: parametric_plot( vector((sin(t), sin(2*t))), (t, 0, 2*pi), color='green')
sage: parametric_plot( vector([t, t+1, t^2]), (t, 0, 1))
TESTS:
sage: parametric_plot((x, t^2), (x, -4, 4))
...
ValueError: there are more variables than variable ranges
sage: parametric_plot((1, x+t), (x, -4, 4))
...
ValueError: there are more variables than variable ranges
sage: parametric_plot((-t, x+t), (x, -4, 4))
...
ValueError: there are more variables than variable ranges
sage: parametric_plot((1, x+t, y), (x, -4, 4), (t, -4, 4))
...
ValueError: there are more variables than variable ranges
sage: parametric_plot((1, x, y), 0, 4)
...
ValueError: there are more variables than variable ranges
Use plot by writing
plot(X, ...)
where  is a Sage object (or list of Sage objects) that
either is callable and returns numbers that can be coerced to
floats, or has a plot method that returns a
GraphicPrimitive object.
is a Sage object (or list of Sage objects) that
either is callable and returns numbers that can be coerced to
floats, or has a plot method that returns a
GraphicPrimitive object.
There are many other specialized 2D plot commands available in Sage, such as plot_slope_field, as well as various graphics primitives like Arrow; type sage.plot.plot? for a current list.
Type plot.options for a dictionary of the default options for plots. You can change this to change the defaults for all future plots. Use plot.reset() to reset to the default options.
PLOT OPTIONS:
APPEARANCE OPTIONS:
The following options affect the appearance of
the line through the points on the graph of  (these are
the same as for the line function):
(these are
the same as for the line function):
INPUT:
Any MATPLOTLIB line option may also be passed in. E.g.,
FILLING OPTIONS: INPUT:
Note that this function does NOT simply sample equally spaced
points between xmin and xmax. Instead it computes equally spaced
points and add small perturbations to them. This reduces the
possibility of, e.g., sampling sin only at multiples of
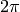 , which would yield a very misleading graph.
, which would yield a very misleading graph.
EXAMPLES: We plot the sin function:
sage: P = plot(sin, (0,10)); print P
Graphics object consisting of 1 graphics primitive
sage: len(P) # number of graphics primitives
1
sage: len(P[0]) # how many points were computed (random)
225
sage: P # render
sage: P = plot(sin, (0,10), plot_points=10); print P
Graphics object consisting of 1 graphics primitive
sage: len(P[0]) # random output
32
sage: P # render
We plot with randomize=False, which makes the initial sample points evenly spaced (hence always the same). Adaptive plotting might insert other points, however, unless adaptive_recursion=0.
sage: p=plot(1, (x,0,3), plot_points=4, randomize=False, adaptive_recursion=0)
sage: list(p[0])
[(0.0, 1.0), (1.0, 1.0), (2.0, 1.0), (3.0, 1.0)]
Some colored functions:
sage: plot(sin, 0, 10, color='purple')
sage: plot(sin, 0, 10, color='#ff00ff')
We plot several functions together by passing a list of functions as input:
sage: plot([sin(n*x) for n in [1..4]], (0, pi))
The function  wiggles wildly near
wiggles wildly near 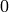 .
Sage adapts to this and plots extra points near the origin.
.
Sage adapts to this and plots extra points near the origin.
sage: plot(sin(1/x), (x, -1, 1))
Via the matplotlib library, Sage makes it easy to tell whether a graph is on both sides of both axes, as the axes only cross if the origin is actually part of the viewing area:
sage: plot(x^3,(x,0,2)) # this one has the origin
sage: plot(x^3,(x,1,2)) # this one does not
Another thing to be aware of with axis labeling is that when
the labels have quite different orders of magnitude or are very
large, scientific notation (the  notation for powers of ten) is used:
notation for powers of ten) is used:
sage: plot(x^2,(x,480,500)) # this one has no scientific notation
sage: plot(x^2,(x,300,500)) # this one has scientific notation on y-axis
Note that the independent variable may be omitted if there is no ambiguity:
sage: plot(sin(1/x), (-1, 1))
The algorithm used to insert extra points is actually pretty simple. On the picture drawn by the lines below:
sage: p = plot(x^2, (-0.5, 1.4)) + line([(0,0), (1,1)], color='green')
sage: p += line([(0.5, 0.5), (0.5, 0.5^2)], color='purple')
sage: p += point(((0, 0), (0.5, 0.5), (0.5, 0.5^2), (1, 1)), color='red', pointsize=20)
sage: p += text('A', (-0.05, 0.1), color='red')
sage: p += text('B', (1.01, 1.1), color='red')
sage: p += text('C', (0.48, 0.57), color='red')
sage: p += text('D', (0.53, 0.18), color='red')
sage: p.show(axes=False, xmin=-0.5, xmax=1.4, ymin=0, ymax=2)
You have the function (in blue) and its approximation (in green) passing through the points A and B. The algorithm finds the midpoint C of AB and computes the distance between C and D. If that distance exceeds the adaptive_tolerance threshold (relative to the size of the initial plot subintervals), the point D is added to the curve. If D is added to the curve, then the algorithm is applied recursively to the points A and D, and D and B. It is repeated adaptive_recursion times (5, by default).
The actual sample points are slightly randomized, so the above plots may look slightly different each time you draw them.
We draw the graph of an elliptic curve as the union of graphs of 2 functions.
sage: def h1(x): return abs(sqrt(x^3 - 1))
sage: def h2(x): return -abs(sqrt(x^3 - 1))
sage: P = plot([h1, h2], 1,4)
sage: P # show the result
We can also directly plot the elliptic curve:
sage: E = EllipticCurve([0,-1])
sage: plot(E, (1, 4), color=hue(0.6))
We can change the line style to one of '--' (two hyphens, yielding dashed), '-.' (dash dot), '-' (solid), 'steps', ':' (dotted):
sage: plot(sin(x), 0, 10, linestyle='-.')
Sage currently ignores points that cannot be evaluated
sage: set_verbose(-1)
sage: plot(-x*log(x), (x,0,1)) # this works fine since the failed endpoint is just skipped.
sage: set_verbose(0)
This prints out a warning and plots where it can (we turn off the warning by setting the verbose mode temporarily to -1.)
sage: set_verbose(-1)
sage: plot(x^(1/3), (x,-1,1))
sage: set_verbose(0)
To plot the negative real cube root, use something like the following:
sage: plot(lambda x : RR(x).nth_root(3), (x,-1, 1))
We can detect the poles of a function:
sage: plot(gamma, (-3, 4), detect_poles = True).show(ymin = -5, ymax = 5)
We draw the Gamma-Function with its poles highlighted:
sage: plot(gamma, (-3, 4), detect_poles = 'show').show(ymin = -5, ymax = 5)
The basic options for filling a plot:
sage: p1 = plot(sin(x), -pi, pi, fill = 'axis')
sage: p2 = plot(sin(x), -pi, pi, fill = 'min')
sage: p3 = plot(sin(x), -pi, pi, fill = 'max')
sage: p4 = plot(sin(x), -pi, pi, fill = 0.5)
sage: graphics_array([[p1, p2], [p3, p4]]).show(frame=True, axes=False)
sage: plot([sin(x), cos(2*x)*sin(4*x)], -pi, pi, fill = {0: 1}, fillcolor = 'red', fillalpha = 1)
A example about the growth of prime numbers:
sage: plot(1.13*log(x), 1, 100, fill = lambda x: nth_prime(x)/floor(x), fillcolor = 'red')
Fill the area between a function and its asymptote:
sage: f = (2*x^3+2*x-1)/((x-2)*(x+1))
sage: plot([f, 2*x+2], -7,7, fill = {0: [1]}, fillcolor='#ccc').show(ymin=-20, ymax=20)
Fill the area between a list of functions and the x-axis:
sage: def b(n): return lambda x: bessel_J(n, x)
sage: plot([b(n) for n in [1..5]], 0, 20, fill = 'axis')
Note that to fill between the ith and jth functions, you must use dictionary key-value pairs i:[j]; key-value pairs like i:j will fill between the ith function and the line y=j:
sage: def b(n): return lambda x: bessel_J(n, x) + 0.5*(n-1)
sage: plot([b(c) for c in [1..5]], 0, 40, fill = dict([(i, [i+1]) for i in [0..3]]))
sage: plot([b(c) for c in [1..5]], 0, 40, fill = dict([(i, i+1) for i in [0..3]]))
Extra options will get passed on to show(), as long as they are valid:
sage: plot(sin(x^2), (x, -3, 3), axes_labels=['$x$','$y$']) # These labels will be nicely typeset
sage: plot(sin(x^2), (x, -3, 3), axes_labels=['x','y']) # These will not
sage: plot(sin(x^2), (x, -3, 3), figsize=[8,2])
sage: plot(sin(x^2), (x, -3, 3)).show(figsize=[8,2]) # These are equivalent
A example with excluded values:
sage: plot(floor(x), (x, 1, 10), exclude = [1..10])
We exclude all points where prime_pi makes a jump:
sage: jumps = [n for n in [1..100] if prime_pi(n) != prime_pi(n-1)]
sage: plot(lambda x: prime_pi(x), (x, 1, 100), exclude = jumps)
Excluded points can also be given by an equation:
sage: g(x) = x^2-2*x-2
sage: plot(1/g(x), (x, -3, 4), exclude = g(x) == 0, ymin = -5, ymax = 5)
TESTS:
We do not randomize the endpoints:
sage: p = plot(x, (x,-1,1))
sage: p[0].xdata[0] == -1
True
sage: p[0].xdata[-1] == 1
True
We check to make sure that the x/y min/max data get set correctly when there are multiple functions.
sage: d = plot([sin(x), cos(x)], 100, 120).get_minmax_data()
sage: d['xmin']
100.0
sage: d['xmax']
120.0
We check various combinations of tuples and functions, ending with tests that lambda functions work properly with explicit variable declaration, without a tuple.
sage: p = plot(lambda x: x,(x,-1,1))
sage: p = plot(lambda x: x,-1,1)
sage: p = plot(x,x,-1,1)
sage: p = plot(x,-1,1)
sage: p = plot(x^2,x,-1,1)
sage: p = plot(x^2,xmin=-1,xmax=2)
sage: p = plot(lambda x: x,x,-1,1)
sage: p = plot(lambda x: x^2,x,-1,1)
sage: p = plot(lambda x: 1/x,x,-1,1)
sage: f(x) = sin(x+3)-.1*x^3
sage: p = plot(lambda x: f(x),x,-1,1)
We check to handle cases where the function gets evaluated at a point which causes an ‘inf’ or ‘-inf’ result to be produced.
sage: p = plot(1/x, 0, 1)
sage: p = plot(-1/x, 0, 1)
Bad options now give better errors:
sage: P = plot(sin(1/x), (x,-1,3), foo=10)
...
RuntimeError: Error in line(): option 'foo' not valid.
polar_plot takes a single function or a list or tuple of functions and plots them with polar coordinates in the given domain.
This function is equivalent to the plot command with the option polar=True. For more help on options, see the documentation for plot.
INPUT:
EXAMPLES:
Here is a blue 8-leaved petal:
sage: polar_plot(sin(5*x)^2, (x, 0, 2*pi), color='blue')
A red figure-8:
sage: polar_plot(abs(sqrt(1 - sin(x)^2)), (x, 0, 2*pi), color='red')
A green limacon of Pascal:
sage: polar_plot(2 + 2*cos(x), (x, 0, 2*pi), color=hue(0.3))
Several polar plots:
sage: polar_plot([2*sin(x), 2*cos(x)], (x, 0, 2*pi))
A filled spiral:
sage: polar_plot(sqrt, 0, 2 * pi, fill = True)
Fill the area between two functions:
sage: polar_plot(cos(4*x) + 1.5, 0, 2*pi, fill=0.5 * cos(4*x) + 2.5, fillcolor='orange').show(aspect_ratio=1)
Fill the area between several spirals:
sage: polar_plot([(1.2+k*0.2)*log(x) for k in range(6)], 1, 3 * pi, fill = {0: [1], 2: [3], 4: [5]})
Exclude points at discontinuities:
sage: polar_plot(log(floor(x)), (x, 1, 4*pi), aspect_ratio = 1, exclude = [1..12])
This function is deprecated. Please use sage.plot.misc.setup_for_eval_on_grid instead. Please note that that function has slightly different calling and return conventions which make it more generally applicable.
INPUT:
OUTPUT:
EXAMPLES:
sage: x,y = var('x,y')
sage: sage.plot.plot.setup_for_eval_on_grid([x^2 + y^2], (x,0,5), (y,0,pi), 11)
doctest:...: DeprecationWarning: sage.plot.plot.setup_for_eval_on_grid is deprecated. Please use sage.plot.misc.setup_for_eval_on_grid; note that that function has slightly different calling and return conventions which make it more generally applicable
([<sage.ext... object at ...>],
0.5,
0.31415926535897931,
(0.0, 5.0),
(0.0, 3.1415926535897931))
We always plot at least two points; one at the beginning and one at the end of the ranges.
sage: sage.plot.plot.setup_for_eval_on_grid([x^2+y^2], (x,0,1), (y,-1,1), 1)
([<sage.ext... object at ...>],
1.0,
2.0,
(0.0, 1.0),
(-1.0, 1.0))
Set the default for showing plots using any plot commands. If called with no arguments, returns the current default.
If this is True (the default) then any plot object when displayed will be displayed as an actual plot instead of text, i.e., the show command is not needed.
EXAMPLES: The default starts out as True:
sage: show_default()
True
We set it to False.
sage: show_default(False)
We see that it is False.
sage: show_default()
False
Now plot commands will not display their plots by default.
Turn back on default display.
sage: show_default(True)
Given a list or tuple or iterable v, coerce each element of v to a float and make a list out of the result.
EXAMPLES:
sage: from sage.plot.plot import to_float_list
sage: to_float_list([1,1/2,3])
[1.0, 0.5, 3.0]
INPUT:
OUTPUT:
EXAMPLES:
sage: from sage.plot.plot import var_and_list_of_values
sage: var_and_list_of_values((var('theta'), 2, 5), 5)
doctest:...: DeprecationWarning: var_and_list_of_values is deprecated. Please use sage.plot.misc.setup_for_eval_on_grid; note that that function has slightly different calling and return conventions which make it more generally applicable
(theta, [2.0, 2.75, 3.5, 4.25, 5.0])
sage: var_and_list_of_values((2, 5), 5)
(None, [2.0, 2.75, 3.5, 4.25, 5.0])
sage: var_and_list_of_values((var('theta'), 2, 5), 2)
(theta, [2.0, 5.0])
sage: var_and_list_of_values((2, 5), 2)
(None, [2.0, 5.0])
Returns two lists (xdata, ydata), each coerced to a list of floats, which correspond to the x-coordinates and the y-coordinates of the points.
The points parameter can be a list of 2-tuples or some object that yields a list of one or two numbers.
This function can potentially be very slow for large point sets.
TESTS:
sage: from sage.plot.plot import xydata_from_point_list
sage: xydata_from_point_list([CC(0), CC(1)]) # ticket 8082
([0.0, 1.0], [0.0, 0.0])