Complex Plots

class sage.plot.complex_plot.ComplexPlot

Bases: sage.plot.primitive.GraphicPrimitive

get_minmax_data()

Returns a dictionary with the bounding box data.

EXAMPLES:

sage: p = complex_plot(lambda z: z, (-1, 2), (-3, 4))
sage: sorted(p.get_minmax_data().items())
[('xmax', 2.0), ('xmin', -1.0), ('ymax', 4.0), ('ymin', -3.0)]

sage.plot.complex_plot.complex_plot(*args, **kwds)

complex_plot takes a complex function of one variable, 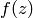and plots output of the function over the specified xrange and yrange as demonstrated below. The magnitude of the output is indicated by the brightness (with zero being black and infinity being white) while the argument is represented by the hue (with red being positive real, and increasing through orange, yellow, ... as the argument increases).

complex_plot(f, (xmin, xmax), (ymin, ymax), ...)

INPUT:

• f – a function of a single complex value
• (xmin, xmax) – 2-tuple, the range of x values
• (ymin, ymax) – 2-tuple, the range of y values

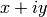
The following inputs must all be passed in as named parameters:

• plot_points – integer (default: 100); number of points to plot in each direction of the grid
• interpolation – string (default: 'catrom'), the interpolation method to use: 'bilinear', 'bicubic', 'spline16', 'spline36', 'quadric', 'gaussian', 'sinc', 'bessel', 'mitchell', 'lanczos', 'catrom', 'hermite', 'hanning', 'hamming', 'kaiser'

EXAMPLES:

Here we plot a couple of simple functions:

sage: complex_plot(sqrt(x), (-5, 5), (-5, 5))
sage: complex_plot(sin(x), (-5, 5), (-5, 5))
sage: complex_plot(log(x), (-10, 10), (-10, 10))
sage: complex_plot(exp(x), (-10, 10), (-10, 10))

A function with some nice zeros and a pole:

sage: f(z) = z^5 + z - 1 + 1/z
sage: complex_plot(f, (-3, 3), (-3, 3))

Here is the identity, useful for seeing what values map to what colors:

sage: complex_plot(lambda z: z, (-3, 3), (-3, 3))

The Riemann Zeta function:

sage: complex_plot(zeta, (-30,30), (-30,30))

Extra options will get passed on to show(), as long as they are valid:

sage: complex_plot(lambda z: z, (-3, 3), (-3, 3), figsize=[1,1])
sage: complex_plot(lambda z: z, (-3, 3), (-3, 3)).show(figsize=[1,1]) # These are equivalent

TESTS:

Test to make sure that using fast_callable functions works:

sage: f(x) = x^2                               
sage: g = fast_callable(f, domain=CC, vars='x')
sage: h = fast_callable(f, domain=CDF, vars='x')
sage: P = complex_plot(f, (-10, 10), (-10, 10))
sage: Q = complex_plot(g, (-10, 10), (-10, 10))
sage: R = complex_plot(h, (-10, 10), (-10, 10))
sage: complex_plot(exp(x)-sin(x), (-10, 10), (-10, 10))

Test to make sure symbolic functions still work without declaring a variable. (We don’t do this in practice because it doesn’t use fast_callable, so it is much slower.)

sage: complex_plot(sqrt, (-5, 5), (-5, 5))

sage.plot.complex_plot.complex_to_rgb(z_values)

INPUT:

• z_values – A grid of complex numbers, as a list of lists

OUTPUT:

An 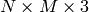floating point Numpy array X, where X[i,j] is an (r,g,b) tuple.

EXAMPLES:

sage: from sage.plot.complex_plot import complex_to_rgb
sage: complex_to_rgb([[0, 1, 1000]])
array([[[ 0.        ,  0.        ,  0.        ],
        [ 0.77172568,  0.        ,  0.        ],
        [ 1.        ,  0.64421177,  0.64421177]]])
sage: complex_to_rgb([[0, 1j, 1000j]])
array([[[ 0.        ,  0.        ,  0.        ],
        [ 0.38586284,  0.77172568,  0.        ],
        [ 0.82210588,  1.        ,  0.64421177]]])