Circles

class sage.plot.circle.Circle(x, y, r, options)

Bases: sage.plot.primitive.GraphicPrimitive

Primitive class for the Circle graphics type. See circle? for information about actually plotting circles.

INPUT:

• x - -coordinate of center of Circle
• y - -coordinate of center of Circle
• r - radius of Circle object
• options - dict of valid plot options to pass to constructor

EXAMPLES:

Note this should normally be used indirectly via circle:

sage: from sage.plot.circle import Circle
sage: C = Circle(2,3,5,{'zorder':2})
sage: C
Circle defined by (2.0,3.0) with r=5.0
sage: C.options()['zorder']
2
sage: C.r
5.0

TESTS:

We test creating a circle:

sage: C = circle((2,3), 5)

get_minmax_data()

Returns a dictionary with the bounding box data.

EXAMPLES:

sage: p = circle((3, 3), 1)
sage: d = p.get_minmax_data()
sage: d['xmin']
2.0
sage: d['ymin']
2.0

plot3d(z=0, **kwds)

Plots a 2D circle (actually a 50-gon) in 3D, with default height zero.

INPUT:

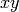• z - optional 3D height above -plane.

EXAMPLES:

sage: circle((0,0), 1).plot3d()

This example uses this method implicitly, but does not pass the optional parameter z to this method:

sage: sum([circle((random(),random()), random()).plot3d(z=random()) for _ in range(20)])

These examples are explicit, and pass z to this method:

sage: C = circle((2,pi), 2, hue=.8, alpha=.3, fill=True)
sage: c = C[0]
sage: d = c.plot3d(z=2)
sage: d.texture.opacity
0.300000000000000

sage: C = circle((2,pi), 2, hue=.8, alpha=.3)
sage: c = C[0]
sage: d = c.plot3d(z=2)
sage: d.jmol_repr(d.testing_render_params())[0][-1]
'color $line_1 translucent 0.7 [204,0,255]'

sage.plot.circle.circle(*args, **kwds)

Return a circle at a point cente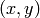r = (or 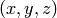and parallel to the 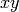-plane) with radius = . Type circle.options to see all options.

OPTIONS:

• alpha - default: 1
• fill - default: False
• thickness - default: 1
• rgbcolor - default: (0,0,0)
• linestyle - default: ‘solid’ (2D plotting only)
• edgecolor - default: ‘black’ (2D plotting only)
• facecolor - default: ‘red’ (2D plotting only, useful only if Fill=True)

EXAMPLES:

sage: c = circle((1,1), 1, rgbcolor=(1,0,0))
sage: c

We can also use this command to plot three-dimensional circles parallel to the 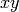-plane:

sage: c = circle((1,1,3), 1, rgbcolor=(1,0,0))
sage: c
sage: type(c)
<class 'sage.plot.plot3d.base.TransformGroup'>

To correct the aspect ratio of certain graphics, it is necessary to show with a figsize of square dimensions:

sage: c.show(figsize=[5,5],xmin=-1,xmax=3,ymin=-1,ymax=3)

Here we make a more complicated plot, with many circles of different colors:

sage: g = Graphics()
sage: step=6; ocur=1/5; paths=16;
sage: PI = math.pi    # numerical for speed -- fine for graphics
sage: for r in range(1,paths+1):
...       for x,y in [((r+ocur)*math.cos(n), (r+ocur)*math.sin(n)) for n in srange(0, 2*PI+PI/step, PI/step)]:
...           g += circle((x,y), ocur, rgbcolor=hue(r/paths))
...       rnext = (r+1)^2
...       ocur = (rnext-r)-ocur
...
sage: g.show(xmin=-(paths+1)^2, xmax=(paths+1)^2, ymin=-(paths+1)^2, ymax=(paths+1)^2, figsize=[6,6])

Note that the rgbcolor option overrides the other coloring options. This produces red fill in a blue circle:

sage: C = circle((2,3), 1, fill=True, edgecolor='blue')

This produces an all-green filled circle:

sage: C = circle((2,3), 1, fill=True, edgecolor='blue', rgbcolor='green')

The option hue overrides all other options, so be careful with its use. This produces a purplish filled circle:

sage: C = circle((2,3), 1, fill=True, edgecolor='blue', rgbcolor='green', hue=.8)

Extra options will get passed on to show(), as long as they are valid:

sage: circle((0, 0), 2, figsize=[10,10]) # That circle is huge!
sage: circle((0, 0), 2).show(figsize=[10,10]) # These are equivalent

TESTS:

We cannot currently plot circles in more than three dimensions:

sage: c = circle((1,1,1,1), 1, rgbcolor=(1,0,0))
...
ValueError: The center of a plotted circle should have two or three coordinates.