Contour Plots

class sage.plot.contour_plot.ContourPlot(xy_data_array, xrange, yrange, options)

Bases: sage.plot.primitive.GraphicPrimitive

Primitive class for the contour plot graphics type. See contour_plot? for help actually doing contour plots.

INPUT:

• xy_data_array - list of lists giving evaluated values of the function on the grid
• xrange - tuple of 2 floats indicating range for horizontal direction
• yrange - tuple of 2 floats indicating range for vertical direction
• options - dict of valid plot options to pass to constructor

EXAMPLES:

Note this should normally be used indirectly via contour_plot:

sage: from sage.plot.contour_plot import ContourPlot
sage: C = ContourPlot([[1,3],[2,4]],(1,2),(2,3),options={})
sage: C
ContourPlot defined by a 2 x 2 data grid
sage: C.xrange
(1, 2)

TESTS:

We test creating a contour plot:

sage: x,y = var('x,y')
sage: C = contour_plot(x^2-y^3+10*sin(x*y), (x, -4, 4), (y, -4, 4),plot_points=121,cmap='hsv')

get_minmax_data()

Returns a dictionary with the bounding box data.

EXAMPLES:

sage: x,y = var('x,y')
sage: f(x,y) = x^2 + y^2
sage: d = contour_plot(f, (3, 6), (3, 6))[0].get_minmax_data()
sage: d['xmin']
3.0
sage: d['ymin']
3.0

sage.plot.contour_plot.contour_plot(*args, **kwds)

contour_plot takes a function of two variables, 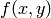and plots contour lines of the function over the specified xrange and yrange as demonstrated below.

contour_plot(f, (xmin, xmax), (ymin, ymax), ...)

INPUT:

• f – a function of two variables
• (xmin, xmax) – 2-tuple, the range of x values OR 3-tuple (x,xmin,xmax)
• (ymin, ymax) – 2-tuple, the range of y values OR 3-tuple (y,ymin,ymax)

The following inputs must all be passed in as named parameters:

• plot_points – integer (default: 100); number of points to plot in each direction of the grid. For old computers, 25 is fine, but should not be used to verify specific intersection points.

• fill – bool (default: True), whether to color in the area between contour lines

• cmap – a colormap (default: 'gray'), the name of a predefined colormap, a list of colors or an instance of a matplotlib Colormap. Type: import matplotlib.cm; matplotlib.cm.datad.keys() for available colormap names.

• contours – integer or list of numbers (default: None): If a list of numbers is given, then this specifies the contour levels to use. If an integer is given, then this many contour lines are used, but the exact levels are determined automatically. If None is passed (or the option is not given), then the number of contour lines is determined automatically, and is usually about 5.

• linewidths – integer or list of integer (default: None), if a single integer all levels will be of the width given, otherwise the levels will be plotted with the width in the order given. If the list is shorter than the number of contours, then the widths will be repeated cyclically.

• linestyles – string or list of strings (default: None), the style of the lines to be plotted, one of: solid, dashed, dashdot, or dotted. If the list is shorter than the number of contours, then the styles will be repeated cyclically.

• labels – boolean (default: False) Show level labels or not.

  The following options are to adjust the style and placement of labels, they have no effect if no labels are shown.

  • label_fontsize – integer (default: 9), the font size of the labels.
  • label_colors – string or sequence of colors (default: None) If a string, gives the name of a single color with which to draw all labels. If a sequence, gives the colors of the labels. A color is a string giving the name of one or a 3-tuple of floats.
  • label_inline – boolean (default: False if fill is True, otherwise True), controls whether the underlying contour is removed or not.
  • label_inline_spacing – integer (default: 3), When inline, this is the amount of contour that is removed from each side, in pixels.
  • label_fmt – a format string (default: “%1.2f”), this is used to get the label text from the level. This can also be a dictionary with the contour levels as keys and corresponding text string labels as values.

• colorbar – boolean (default: False) Show a colorbar or not.

  The following options are to adjust the style and placement of colorbars. They have no effect if a colorbar is not shown.

  • colorbar_orientation – string (default: ‘vertical’), controls placement of the colorbar, can be either ‘vertical’ or ‘horizontal’
  • colorbar_format – a format string, this is used to format the colorbar labels.
  • colorbar_spacing – string (default: ‘proportional’). If ‘proportional’, make the contour divisions proportional to values. If ‘uniform’, space the colorbar divisions uniformly, without regard for numeric values.

EXAMPLES:

Here we plot a simple function of two variables. Note that since the input function is an expression, we need to explicitly declare the variables in 3-tuples for the range:

sage: x,y = var('x,y')
sage: contour_plot(cos(x^2+y^2), (x, -4, 4), (y, -4, 4))

Here we change the ranges and add some options:

sage: x,y = var('x,y')
sage: contour_plot((x^2)*cos(x*y), (x, -10, 5), (y, -5, 5), fill=False, plot_points=150)

An even more complicated plot:

sage: x,y = var('x,y')
sage: contour_plot(sin(x^2 + y^2)*cos(x)*sin(y), (x, -4, 4), (y, -4, 4),plot_points=150)

Some elliptic curves, but with symbolic endpoints. In the first example, the plot is rotated 90 degrees because we switch the variables , :

sage: x,y = var('x,y')
sage: contour_plot(y^2 + 1 - x^3 - x, (y,-pi,pi), (x,-pi,pi))

sage: contour_plot(y^2 + 1 - x^3 - x, (x,-pi,pi), (y,-pi,pi))

We can play with the contour levels:

sage: x,y = var('x,y')
sage: f(x,y) = x^2 + y^2
sage: contour_plot(f, (-2, 2), (-2, 2))

sage: contour_plot(f, (-2, 2), (-2, 2), contours=2, cmap=[(1,0,0), (0,1,0), (0,0,1)])

sage: contour_plot(f, (-2, 2), (-2, 2), contours=(0.1, 1.0, 1.2, 1.4), cmap='hsv')

sage: contour_plot(f, (-2, 2), (-2, 2), contours=(1.0,), fill=False, aspect_ratio=1)

sage: contour_plot(x-y^2,(x,-5,5),(y,-3,3),contours=[-4,0,1])

We can change the style of the lines:

sage: contour_plot(f, (-2,2), (-2,2), fill=False, linewidths=10)

sage: contour_plot(f, (-2,2), (-2,2), fill=False, linestyles='dashdot')

sage: P=contour_plot(x^2-y^2,(x,-3,3),(y,-3,3),contours=[0,1,2,3,4],\
...    linewidths=[1,5],linestyles=['solid','dashed'],fill=False)
sage: P

sage: P=contour_plot(x^2-y^2,(x,-3,3),(y,-3,3),contours=[0,1,2,3,4],\
...    linewidths=[1,5],linestyles=['solid','dashed'])
sage: P

We can add labels and play with them:

sage: contour_plot(y^2 + 1 - x^3 - x, (x,-pi,pi), (y,-pi,pi),  fill=False, cmap='hsv', labels=True)

sage: P=contour_plot(y^2 + 1 - x^3 - x, (x,-pi,pi), (y,-pi,pi), fill=False, cmap='hsv',\
...     labels=True, label_fmt="%1.0f", label_colors='black')
sage: P

sage: P=contour_plot(y^2 + 1 - x^3 - x, (x,-pi,pi), (y,-pi,pi), fill=False, cmap='hsv',labels=True,\
...    contours=[-4,0,4],  label_fmt={-4:"low", 0:"medium", 4: "hi"}, label_colors='black')
sage: P

sage: P=contour_plot(y^2 + 1 - x^3 - x, (x,-pi,pi), (y,-pi,pi), \
...    fill=False, cmap='hsv', labels=True, label_fontsize=18)
sage: P

sage: P=contour_plot(y^2 + 1 - x^3 - x, (x,-pi,pi), (y,-pi,pi), \
...    fill=False, cmap='hsv', labels=True, label_inline_spacing=1)
sage: P

sage: P= contour_plot(y^2 + 1 - x^3 - x, (x,-pi,pi), (y,-pi,pi), \
...    fill=False, cmap='hsv', labels=True, label_inline=False)
sage: P

We can change the color of the labels if so desired:

sage: contour_plot(f, (-2,2), (-2,2), labels=True, label_colors='red')

We can add a colorbar as well:

sage: f(x,y)=x^2-y^2
sage: contour_plot(f, (x,-3,3), (y,-3,3), colorbar=True)

sage: contour_plot(f, (x,-3,3), (y,-3,3), colorbar=True,colorbar_orientation='horizontal')

sage: contour_plot(f, (x,-3,3), (y,-3,3), contours=[-2,-1,4],colorbar=True)

sage: contour_plot(f, (x,-3,3), (y,-3,3), contours=[-2,-1,4],colorbar=True,colorbar_spacing='uniform')

sage: contour_plot(f, (x,-3,3), (y,-3,3), contours=[0,2,3,6],colorbar=True,colorbar_format='%.3f')

sage: contour_plot(f, (x,-3,3), (y,-3,3), labels=True,label_colors='red',contours=[0,2,3,6],colorbar=True)

sage: contour_plot(f, (x,-3,3), (y,-3,3), cmap='winter', contours=20, fill=False, colorbar=True)

This should plot concentric circles centered at the origin:

sage: x,y = var('x,y')
sage: contour_plot(x^2+y^2-2,(x,-1,1), (y,-1,1)).show(aspect_ratio=1) 

Extra options will get passed on to show(), as long as they are valid:

sage: f(x, y) = cos(x) + sin(y)
sage: contour_plot(f, (0, pi), (0, pi), axes=True)

sage: contour_plot(f, (0, pi), (0, pi)).show(axes=True) # These are equivalent

Note that with fill=False and grayscale contours, there is the possibility of confusion between the contours and the axes, so use fill=False together with axes=True with caution:

sage: contour_plot(f, (-pi, pi), (-pi, pi), fill=False, axes=True) 

TESTS:

To check that ticket 5221 is fixed, note that this has three curves, not two:

sage: x,y = var('x,y')
sage: contour_plot(x-y^2,(x,-5,5),(y,-3,3),contours=[-4,-2,0], fill=False)

sage.plot.contour_plot.equify(f)

Returns the equation rewritten as a symbolic function to give negative values when True, positive when False.

EXAMPLES:

sage: from sage.plot.contour_plot import equify
sage: var('x, y')
(x, y)
sage: equify(x^2 < 2)
x^2 - 2
sage: equify(x^2 > 2)
-x^2 + 2
sage: equify(x*y > 1)
-x*y + 1
sage: equify(y > 0)
-y
sage: f=equify(lambda x,y: x>y)
sage: f(1,2)
1
sage: f(2,1)
-1

sage.plot.contour_plot.implicit_plot(*args, **kwds)

implicit_plot takes a function of two variables, 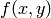and plots the curve 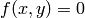over the specified xrange and yrange as demonstrated below.

implicit_plot(f, (xmin, xmax), (ymin, ymax), ...)

implicit_plot(f, (x, xmin, xmax), (y, ymin, ymax), ...)

INPUT:

• f – a function of two variables or equation in two variables
• (xmin, xmax) – 2-tuple, the range of x values or (x,xmin,xmax)
• (ymin, ymax) – 2-tuple, the range of y values or (y,ymin,ymax)

The following inputs must all be passed in as named parameters:

• plot_points – integer (default: 150); number of points to plot in each direction of the grid
• fill – boolean (default: False); if True, fill the region .
• linewidth – integer (default: None), if a single integer all levels will be of the width given, otherwise the levels will be plotted with the widths in the order given.
• linestyle – string (default: None), the style of the line to be plotted, one of: solid, dashed, dashdot or dotted.

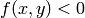EXAMPLES:

A simple circle with a radius of 2. Note that since the input function is an expression, we need to explicitly declare the variables in 3-tuples for the range:

sage: var("x y")
(x, y)
sage: implicit_plot(x^2+y^2-2, (x,-3,3), (y,-3,3)).show(aspect_ratio=1)

I can do the same thing, but using a callable function so I don’t need to explicitly define the variables in the ranges, and filling the inside:

sage: x,y = var('x,y')
sage: f(x,y) = x^2 + y^2 - 2
sage: implicit_plot(f, (-3, 3), (-3, 3),fill=True).show(aspect_ratio=1)

The same circle but with a different line width:

sage: implicit_plot(f, (-3,3), (-3,3), linewidth=6).show(aspect_ratio=1)

And again the same circle but this time with a dashdot border:

sage: implicit_plot(f, (-3,3), (-3,3), linestyle='dashdot').show(aspect_ratio=1)

You can also plot an equation:

sage: var("x y")
(x, y)
sage: implicit_plot(x^2+y^2 == 2, (x,-3,3), (y,-3,3)).show(aspect_ratio=1)

We can define a level- approximation of the boundary of the Mandelbrot set:

sage: def mandel(n):
...       c = polygen(CDF, 'c')
...       z = 0
...       for i in range(n):
...           z = z*z + c
...       def f(x, y):
...           val = z(CDF(x, y))
...           return val.norm() - 4
...       return f

The first-level approximation is just a circle:

sage: implicit_plot(mandel(1), (-3, 3), (-3, 3)).show(aspect_ratio=1)

A third-level approximation starts to get interesting:

sage: implicit_plot(mandel(3), (-2, 1), (-1.5, 1.5)).show(aspect_ratio=1)

The seventh-level approximation is a degree 64 polynomial, and implicit_plot does a pretty good job on this part of the curve. (plot_points=200 looks even better, but it takes over a second.)

sage: implicit_plot(mandel(7), (-0.3, 0.05), (-1.15, -0.9),plot_points=50).show(aspect_ratio=1)

sage.plot.contour_plot.region_plot(*args, **kwds)

region_plot takes a boolean function of two variables, 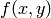and plots the region where f is True over the specified xrange and yrange as demonstrated below.

region_plot(f, (xmin, xmax), (ymin, ymax), ...)

INPUT:

• f – a boolean function of two variables
• (xmin, xmax) – 2-tuple, the range of x values OR 3-tuple (x,xmin,xmax)
• (ymin, ymax) – 2-tuple, the range of y values OR 3-tuple (y,ymin,ymax)
• plot_points – integer (default: 100); number of points to plot in each direction of the grid
• incol – a color (default: 'blue'), the color inside the region
• outcol – a color (default: 'white'), the color of the outside of the region

If any of these options are specified, the border will be shown as indicated, otherwise it is only implicit (with color incol) as the border of the inside of the region.

• bordercol – a color (default: None), the color of the border ('black' if borderwidth or borderstyle is specified but not bordercol)

• borderstyle – string (default: ‘solid’), one of ‘solid’, ‘dashed’, ‘dotted’, ‘dashdot’
• borderwidth – integer (default: None), the width of the border in pixels

EXAMPLES:

Here we plot a simple function of two variables:

sage: x,y = var('x,y')
sage: region_plot(cos(x^2+y^2) <= 0, (x, -3, 3), (y, -3, 3))

Here we play with the colors:

sage: region_plot(x^2+y^3 < 2, (x, -2, 2), (y, -2, 2), incol='lightblue', bordercol='gray')

An even more complicated plot, with dashed borders:

sage: region_plot(sin(x)*sin(y) >= 1/4, (x,-10,10), (y,-10,10), incol='yellow', bordercol='black', borderstyle='dashed', plot_points=250)

A disk centered at the origin:

sage: region_plot(x^2+y^2<1, (x,-1,1), (y,-1,1), aspect_ratio=1)

A plot with more than one condition (all conditions must be true for the statement to be true):

sage: region_plot([x^2+y^2<1, x<y], (x,-2,2), (y,-2,2), aspect_ratio=1)

Since it doesn’t look very good, let’s increase plot_points:

sage: region_plot([x^2+y^2<1, x<y], (x,-2,2), (y,-2,2), plot_points=400, aspect_ratio=1)

To get plots where only one condition needs to be true, use a function:

sage: region_plot(lambda x,y: x^2+y^2<1 or x<y, (x,-2,2), (y,-2,2), aspect_ratio=1)

The first quadrant of the unit circle:

sage: region_plot([y>0, x>0, x^2+y^2<1], (x,-1.1, 1.1), (y,-1.1, 1.1), plot_points = 400, aspect_ratio=1)

Here is another plot, with a huge border:

sage: region_plot(x*(x-1)*(x+1)+y^2<0, (x, -3, 2), (y, -3, 3), incol='lightblue', bordercol='gray', borderwidth=10, plot_points=50)

If we want to keep only the region where x is positive:

sage: region_plot([x*(x-1)*(x+1)+y^2<0, x>-1], (x, -3, 2), (y, -3, 3), incol='lightblue', plot_points=50)

Here we have a cut circle:

sage: region_plot([x^2+y^2<4, x>-1], (x, -2, 2), (y, -2, 2), incol='lightblue', bordercol='gray', plot_points=200, aspect_ratio=1)

The first variable range corresponds to the horizontal axis and the second variable range corresponds to the vertical axis:

sage: s,t=var('s,t')
sage: region_plot(s>0,(t,-2,2),(s,-2,2))
sage: region_plot(s>0,(s,-2,2),(t,-2,2))