Points

TESTS:

sage: E = EllipticCurve('37a')
sage: P = E(0,0)
sage: def get_points(n): return sum([point(list(i*P)[:2], size=3) for i in range(-n,n) if i != 0 and (i*P)[0] < 3])
sage: sum([get_points(15*n).plot3d(z=n) for n in range(1,10)])

class sage.plot.point.Point(xdata, ydata, options)

Bases: sage.plot.primitive.GraphicPrimitive_xydata

Primitive class for the point graphics type. See point?, point2d? or point3d? for information about actually plotting points.

INPUT:

• xdata - list of x values for points in Point object
• ydata - list of y values for points in Point object
• options - dict of valid plot options to pass to constructor

EXAMPLES:

Note this should normally be used indirectly via point and friends:

sage: from sage.plot.point import Point
sage: P = Point([1,2],[2,3],{'alpha':.5})
sage: P
Point set defined by 2 point(s)
sage: P.options()['alpha']
0.500000000000000
sage: P.xdata
[1, 2]

TESTS:

We test creating a point:

sage: P = point((3,3))

plot3d(z=0, **kwds)

Plots a two-dimensional point in 3-D, with default height zero.

INPUT:

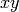• z - optional 3D height above -plane. May be a list if self is a list of points.

EXAMPLES:

One point:

sage: A=point((1,1))
sage: a=A[0];a
Point set defined by 1 point(s)
sage: b=a.plot3d()

One point with a height:

sage: A=point((1,1))
sage: a=A[0];a
Point set defined by 1 point(s)
sage: b=a.plot3d(z=3)
sage: b.loc[2]
3.0

Multiple points:

sage: P=point([(0,0), (1,1)])
sage: p=P[0]; p
Point set defined by 2 point(s)
sage: q=p.plot3d(size=22)

Multiple points with different heights:

sage: P=point([(0,0), (1,1)])
sage: p=P[0]
sage: q=p.plot3d(z=[2,3])
sage: q.all[0].loc[2]
2.0
sage: q.all[1].loc[2]
3.0

Note that keywords passed must be valid point3d options:

sage: A=point((1,1),size=22)
sage: a=A[0];a
Point set defined by 1 point(s)
sage: b=a.plot3d()
sage: b.size
22
sage: b=a.plot3d(pointsize=23) # only 2D valid option
sage: b.size
22
sage: b=a.plot3d(size=23) # correct keyword
sage: b.size
23

TESTS:

Heights passed as a list should have same length as number of points:

sage: P=point([(0,0), (1,1), (2,3)])
sage: p=P[0]
sage: q=p.plot3d(z=2)
sage: q.all[1].loc[2]
2.0
sage: q=p.plot3d(z=[2,-2])
...
ValueError: Incorrect number of heights given

sage.plot.point.point(points, **kwds)

Returns either a 2-dimensional or 3-dimensional point or sum of points.

INPUT:

• points - either a single point (as a tuple) or a list of points.

For information regarding additional arguments, see either point2d? or point3d?.

EXAMPLES:

sage: point((1,2))
sage: point((1,2,3))
sage: point([(0,0), (1,1)])
sage: point([(0,0,1), (1,1,1)])

Extra options will get passed on to show(), as long as they are valid:

sage: point([(cos(theta), sin(theta)) for theta in srange(0, 2*pi, pi/8)], frame=True)
sage: point([(cos(theta), sin(theta)) for theta in srange(0, 2*pi, pi/8)]).show(frame=True) # These are equivalent

sage.plot.point.point2d(*args, **kwds)

A point of size size defined by point = 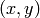. Point takes either a single tuple of coordinates or a list of tuples.

Type point2d.options to see all options.

EXAMPLES:

A purple point from a single tuple or coordinates:

sage: point((0.5, 0.5), rgbcolor=hue(0.75))

If you need a 2D point to live in 3-space later, this is possible:

sage: A=point((1,1))
sage: a=A[0];a
Point set defined by 1 point(s)
sage: b=a.plot3d(z=3)

This is also true with multiple points:

sage: P=point([(0,0), (1,1)])
sage: p=P[0]
sage: q=p.plot3d(z=[2,3])

Here are some random larger red points, given as a list of tuples:

sage: point(((0.5, 0.5), (1, 2), (0.5, 0.9), (-1, -1)), rgbcolor=hue(1), size=30)

Extra options will get passed on to show(), as long as they are valid:

sage: point([(cos(theta), sin(theta)) for theta in srange(0, 2*pi, pi/8)], frame=True)
sage: point([(cos(theta), sin(theta)) for theta in srange(0, 2*pi, pi/8)]).show(frame=True) # These are equivalent

Since Sage Version 4.4 (ticket #8599), the size of a 2d point can be given by the argument size instead of pointsize. The argument pointsize is still supported:

sage: point((3,4), size=100)
sage: point((3,4), pointsize=100)

sage.plot.point.points(points, **kwds)

Returns either a 2-dimensional or 3-dimensional point or sum of points.

INPUT:

• points - either a single point (as a tuple) or a list of points.

For information regarding additional arguments, see either point2d? or point3d?.

EXAMPLES:

sage: point((1,2))
sage: point((1,2,3))
sage: point([(0,0), (1,1)])
sage: point([(0,0,1), (1,1,1)])

Extra options will get passed on to show(), as long as they are valid:

sage: point([(cos(theta), sin(theta)) for theta in srange(0, 2*pi, pi/8)], frame=True)
sage: point([(cos(theta), sin(theta)) for theta in srange(0, 2*pi, pi/8)]).show(frame=True) # These are equivalent