Density Plots

class sage.plot.density_plot.DensityPlot(xy_data_array, xrange, yrange, options)

Bases: sage.plot.primitive.GraphicPrimitive

Primitive class for the density plot graphics type. See density_plot? for help actually doing density plots.

INPUT:

• xy_data_array - list of lists giving evaluated values of the function on the grid
• xrange - tuple of 2 floats indicating range for horizontal direction
• yrange - tuple of 2 floats indicating range for vertical direction
• options - dict of valid plot options to pass to constructor

EXAMPLES:

Note this should normally be used indirectly via :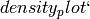

sage: from sage.plot.density_plot import DensityPlot
sage: D = DensityPlot([[1,3],[2,4]],(1,2),(2,3),options={})
sage: D
DensityPlot defined by a 2 x 2 data grid
sage: D.yrange
(2, 3)
sage: D.options()
{}

TESTS:

We test creating a density plot:

sage: x,y = var('x,y')
sage: D = density_plot(x^2-y^3+10*sin(x*y), (x, -4, 4), (y, -4, 4),plot_points=121,cmap='hsv')

get_minmax_data()

Returns a dictionary with the bounding box data.

EXAMPLES:

sage: x,y = var('x,y')
sage: f(x, y) = x^2 + y^2
sage: d = density_plot(f, (3, 6), (3, 6))[0].get_minmax_data()
sage: d['xmin']
3.0
sage: d['ymin']
3.0

sage.plot.density_plot.density_plot(*args, **kwds)

density_plot takes a function of two variables, 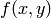and plots the height of of the function over the specified xrange and yrange as demonstrated below.

density_plot(f, (xmin, xmax), (ymin, ymax), ...)

INPUT:

• f – a function of two variables
• (xmin, xmax) – 2-tuple, the range of x values OR 3-tuple (x,xmin,xmax)
• (ymin, ymax) – 2-tuple, the range of y values OR 3-tuple (y,ymin,ymax)

The following inputs must all be passed in as named parameters:

• plot_points – integer (default: 25); number of points to plot in each direction of the grid
• cmap – a colormap (type cmap_help() for more information).
• interpolation – string (default: 'catrom'), the interpolation method to use: 'bilinear', 'bicubic', 'spline16', 'spline36', 'quadric', 'gaussian', 'sinc', 'bessel', 'mitchell', 'lanczos', 'catrom', 'hermite', 'hanning', 'hamming', 'kaiser'

EXAMPLES:

Here we plot a simple function of two variables. Note that since the input function is an expression, we need to explicitly declare the variables in 3-tuples for the range:

sage: x,y = var('x,y')
sage: density_plot(sin(x)*sin(y), (x, -2, 2), (y, -2, 2))

Here we change the ranges and add some options; note that here f is callable (has variables declared), so we can use 2-tuple ranges:

sage: x,y = var('x,y')
sage: f(x,y) = x^2*cos(x*y)
sage: density_plot(f, (x,-10,5), (y, -5,5), interpolation='sinc', plot_points=100)

An even more complicated plot:

sage: x,y = var('x,y')
sage: density_plot(sin(x^2 + y^2)*cos(x)*sin(y), (x, -4, 4), (y, -4, 4), cmap='jet', plot_points=100)

This should show a “spotlight” right on the origin:

sage: x,y = var('x,y') 
sage: density_plot(1/(x^10+y^10), (x, -10, 10), (y, -10, 10)) 

Some elliptic curves, but with symbolic endpoints. In the first example, the plot is rotated 90 degrees because we switch the variables , :

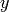sage: density_plot(y^2 + 1 - x^3 - x, (y,-pi,pi), (x,-pi,pi))
sage: density_plot(y^2 + 1 - x^3 - x, (x,-pi,pi), (y,-pi,pi))

Extra options will get passed on to show(), as long as they are valid:

sage: density_plot(log(x) + log(y), (x, 1, 10), (y, 1, 10), dpi=20)
sage: density_plot(log(x) + log(y), (x, 1, 10), (y, 1, 10)).show(dpi=20) # These are equivalent