Line Plots

class sage.plot.line.Line(xdata, ydata, options)

Bases: sage.plot.primitive.GraphicPrimitive_xydata

Primitive class that initializes the line graphics type.

EXAMPLES:

sage: from sage.plot.line import Line
sage: Line([1,2,7], [1,5,-1], {})
Line defined by 3 points

plot3d(**kwds)

EXAMPLES:

sage: EllipticCurve('37a').plot(thickness=5).plot3d()

sage.plot.line.line(points, **kwds)

Returns either a 2-dimensional or 3-dimensional line depending on value of points.

For information regarding additional arguments, see either line2d? or line3d?.

EXAMPLES:

sage: line([(0,0), (1,1)])
sage: line([(0,0,1), (1,1,1)])

sage.plot.line.line2d(*args, **kwds)

Create the line through the given list of points.

Type code{line2d.options} for a dictionary of the default options for lines. You can change this to change the defaults for all future lines. Use code{line2d.reset()} to reset to the default options.

INPUT:

• alpha – How transparent the line is
• thickness – How thick the line is
• rgbcolor – The color as an RGB tuple
• hue – The color given as a hue

Any MATPLOTLIB line option may also be passed in. E.g.,

• linestyle – The style of the line, which is one of:
  • '--' (dashed)
  • '-.' (dash dot)
  • '-' (solid)
  • 'steps'
  • ':' (dotted)
• marker – The style of the marker, which is one of:
  • '0' (tickleft)
  • '1' (tickright)
  • '2' (tickup)
  • '3' (tickdown)
  • '' (nothing)
  • ' ' (nothing)
  • '+' (plus)
  • ',' (pixel)
  • '.' (point)
  • '1' (tri_down)
  • '3' (tri_left)
  • '2' (tri_up)
  • '4' (tri_right)
  • '<' (triangle_left)
  • '>' (triangle_right)
  • 'None' (nothing)
  • 'D' (diamond)
  • 'H' (hexagon2)
  • '_' (hline)
  • '\^' (triangle_up)
  • 'd' (thin_diamond)
  • 'h' (hexagon1)
  • 'o' (circle)
  • 'p' (pentagon)
  • 's' (square)
  • 'v' (triangle_down)
  • 'x' (x)
  • '|' (vline)
• markersize – the size of the marker in points
• markeredgecolor – the markerfacecolor can be any color arg
• markeredgewidth – the size of the marker edge in points

EXAMPLES:

A blue conchoid of Nicomedes:

sage: L = [[1+5*cos(pi/2+pi*i/100), tan(pi/2+pi*i/100)*(1+5*cos(pi/2+pi*i/100))] for i in range(1,100)]
sage: line(L, rgbcolor=(1/4,1/8,3/4))

A line with 2 complex points:

sage: i = CC.0
sage: line([1+i, 2+3*i])

A blue hypotrochoid (3 leaves):

sage: n = 4; h = 3; b = 2
sage: L = [[n*cos(pi*i/100)+h*cos((n/b)*pi*i/100),n*sin(pi*i/100)-h*sin((n/b)*pi*i/100)] for i in range(200)]
sage: line(L, rgbcolor=(1/4,1/4,3/4))

A blue hypotrochoid (4 leaves):

sage: n = 6; h = 5; b = 2
sage: L = [[n*cos(pi*i/100)+h*cos((n/b)*pi*i/100),n*sin(pi*i/100)-h*sin((n/b)*pi*i/100)] for i in range(200)]
sage: line(L, rgbcolor=(1/4,1/4,3/4))

A red limacon of Pascal:

sage: L = [[sin(pi*i/100)+sin(pi*i/50),-(1+cos(pi*i/100)+cos(pi*i/50))] for i in range(-100,101)]
sage: line(L, rgbcolor=(1,1/4,1/2))

A light green trisectrix of Maclaurin:

sage: L = [[2*(1-4*cos(-pi/2+pi*i/100)^2),10*tan(-pi/2+pi*i/100)*(1-4*cos(-pi/2+pi*i/100)^2)] for i in range(1,100)]
sage: line(L, rgbcolor=(1/4,1,1/8))

A green lemniscate of Bernoulli:

sage: cosines = [cos(-pi/2+pi*i/100) for i in range(201)]
sage: v = [(1/c, tan(-pi/2+pi*i/100)) for i,c in enumerate(cosines) if c != 0]
sage: L = [(a/(a^2+b^2), b/(a^2+b^2)) for a,b in v]
sage: line(L, rgbcolor=(1/4,3/4,1/8))

A red plot of the Jacobi elliptic function , :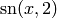

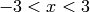sage: L = [(i/100.0, jacobi('sn', i/100.0 ,2.0)) for i in range(-300,300,30)]    
sage: line(L, rgbcolor=(3/4,1/4,1/8))

A red plot of 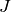-Bessel function , :

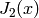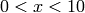sage: L = [(i/10.0, bessel_J(2,i/10.0)) for i in range(100)]
sage: line(L, rgbcolor=(3/4,1/4,5/8))    

A purple plot of the Riemann zeta function , :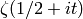

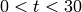sage: i = CDF.gen()
sage: v = [zeta(0.5 + n/10 * i) for n in range(300)]
sage: L = [(z.real(), z.imag()) for z in v]
sage: line(L, rgbcolor=(3/4,1/2,5/8))

A purple plot of the Hasse-Weil -function , :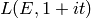

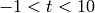sage: E = EllipticCurve('37a')
sage: vals = E.lseries().values_along_line(1-I, 1+10*I, 100) # critical line
sage: L = [(z[1].real(), z[1].imag()) for z in vals]
sage: line(L, rgbcolor=(3/4,1/2,5/8))

A red, blue, and green “cool cat”:

sage: G = plot(-cos(x), -2, 2, thickness=5, rgbcolor=(0.5,1,0.5))
sage: P = polygon([[1,2], [5,6], [5,0]], rgbcolor=(1,0,0))
sage: Q = polygon([(-x,y) for x,y in P[0]], rgbcolor=(0,0,1))
sage: G + P + Q   # show the plot

A line with no points or one point:

sage: line([])
sage: line([(1,1)])

Extra options will get passed on to show(), as long as they are valid:

sage: line([(0,1), (3,4)], figsize=[10, 2])
sage: line([(0,1), (3,4)]).show(figsize=[10, 2]) # These are equivalent