Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Combinatorics »
- Crystals »

Bases: sage.combinat.crystals.tensor_product.CrystalOfWords
Crystals of tableaux. Input: a Cartan Type type and “shape”, a partition of length <= type[1]. Produces a classical crystal with the given Cartan Type and highest weight corresponding to the given shape.
If the type is [‘D’,r] then the shape is permitted to have a
negative value in the r-th position. Thus if
shape=`[s_1,s_2,...,s_r]` then s_r may be negative but
in any case 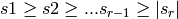 . This
crystal is related to
. This
crystal is related to ![[s_1,\cdots,|s_r|]](../../../_images/math/e7e11f6acda1e3f19aeb8584769509f72af1f15c.png) by the outer
automorphism of SO(2r).
by the outer
automorphism of SO(2r).
Note that crystals of tableaux are constructed using an embedding into tensor products following Kashiwara and Nakashima [Kashiwara, Masaki; Nakashima, Toshiki, Crystal graphs for representations of the q-analogue of classical Lie algebras, J. Algebra 165 (1994), no. 2, 295-345.]. Sage’s tensor product rule for crystals differs from that of Kashiwara and Nakashima by reversing the order of the tensor factors. Sage produces the same crystals of tableaux as Kashiwara and Nakashima. With Sage’s convention, the tensor product of crystals is the same as the monoid operation on tableaux and hence the plactic monoid.
EXAMPLES:
We create the crystal of tableaux for type 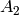 , with
highest weight given by the partition [2,1,1]:
, with
highest weight given by the partition [2,1,1]:
sage: Tab = CrystalOfTableaux(['A',3], shape = [2,1,1])
Here is the list of its elements:
sage: Tab.list()
[[[1, 1], [2], [3]], [[1, 2], [2], [3]], [[1, 3], [2], [3]],
[[1, 4], [2], [3]], [[1, 4], [2], [4]], [[1, 4], [3], [4]],
[[2, 4], [3], [4]], [[1, 1], [2], [4]], [[1, 2], [2], [4]],
[[1, 3], [2], [4]], [[1, 3], [3], [4]], [[2, 3], [3], [4]],
[[1, 1], [3], [4]], [[1, 2], [3], [4]], [[2, 2], [3], [4]]]
One can get (currently) crude plotting via:
# sage: Tab.plot() # random
One can get instead get a LaTeX drawing ready to be copy-pasted into a LaTeX file:
# sage: Tab.latex() # random
See sage.combinat.crystals.crystals? for general help on using crystals
Internally, a tableau of a given Cartan type is represented as a tensor product of letters of the same type. The order in which the tensor factors appear is by reading the columns of the tableaux left to right, top to bottom (in French notation). As an example:
sage: T = CrystalOfTableaux(['A',2], shape = [3,2])
sage: T.module_generators[0]
[[1, 1, 1], [2, 2]]
sage: T.module_generators[0]._list
[2, 1, 2, 1, 1]
To create a tableau, one can use:
sage: Tab = CrystalOfTableaux(['A',3], shape = [2,2])
sage: Tab(rows=[[1,2],[3,4]])
[[1, 2], [3, 4]]
sage: Tab(columns=[[3,1],[4,2]])
[[1, 2], [3, 4]]
FIXME: do we want to specify the columns increasingly or decreasingly That is, should this be Tab(columns = [[1,3],[2,4]])
TODO: make this fully consistent with Tableau!
TESTS:
Base cases:
sage: T = CrystalOfTableaux(['A',2], shape = [])
sage: T.list()
[[]]
sage: T = CrystalOfTableaux(['C',2], shape = [1])
sage: TestSuite(T).run()
sage: T.list()
[[[1]], [[2]], [[-2]], [[-1]]]
sage: T = CrystalOfTableaux(['A',2], shapes = [[],[1],[2]])
sage: T.list()
[[], [[1]], [[2]], [[3]], [[1, 1]], [[1, 2]], [[2, 2]], [[1, 3]], [[2, 3]], [[3, 3]]]
sage: T.module_generators
([], [[1]], [[1, 1]])
sage: T = CrystalOfTableaux(['B',2],shape=[3])
sage: T(rows=[[1,1,0]])
[[1, 1, 0]]
Input tests:
sage: Tab = CrystalOfTableaux(['A',3], shape = [2,2])
sage: C = Tab.letters
sage: Tab(rows = [[1,2],[3,4]])._list == [C(3),C(1),C(4),C(2)]
True
sage: Tab(columns = [[3,1],[4,2]])._list == [C(3),C(1),C(4),C(2)]
True
And for compatibility with TensorProductOfCrystal we should also allow as input the internal list / sequence of elements:
sage: Tab(list = [3,1,4,2])._list == [C(3),C(1),C(4),C(2)]
True
sage: Tab(3,1,4,2)._list == [C(3),C(1),C(4),C(2)]
True
Type D, illustrating that the last parameter in the shape can be negative:
sage: C = CrystalOfTableaux(['D',4],shape=[1,1,1,-1])
sage: C.cardinality()
35
sage: TestSuite(C).run()
The next example checks whether a given tableau is in fact a valid type C tableau or not:
sage: T = CrystalOfTableaux([‘C’,3], shape = [2,2,2]) sage: t = T(rows=[[1,3],[2,-3],[3,-1]]) sage: t in T.list() True sage: t = T(rows=[[2,3],[3,-3],[-3,-2]]) sage: t in T.list() False
Returns the Cartan type of the associated crystal
This yields the module generator (or highest weight element) of a classical crystal of given shape. The module generator is the unique tableau with equal shape and content.
Bases: sage.combinat.crystals.tensor_product.TensorProductOfCrystalsElement
EXAMPLES:
sage: T = CrystalOfTableaux(['A',3], shape = [2,2])
sage: t = T(rows=[[1,2],[3,4]])
sage: t.pp()
1 2
3 4
Promotion for type A crystals of tableaux of rectangular shape
Returns the result of applying promotion on this tableau.
This method only makes sense in type A with rectangular shapes.
EXAMPLES:
sage: C = CrystalOfTableaux(["A",3], shape = [3,3,3])
sage: t = C(Tableau([[1,1,1],[2,2,3],[3,4,4]]))
sage: t
[[1, 1, 1], [2, 2, 3], [3, 4, 4]]
sage: t.promotion()
[[1, 1, 2], [2, 2, 3], [3, 4, 4]]
sage: t.promotion().parent()
The crystal of tableaux of type ['A', 3] and shape(s) [[3, 3, 3]]
Inverse promotion for type A crystals of tableaux of rectangular shape
Returns the result of applying inverse promotion on this tableau.
This method only makes sense in type A with rectangular shapes.
EXAMPLES:
sage: C = CrystalOfTableaux(["A",3], shape = [3,3,3])
sage: t = C(Tableau([[1,1,1],[2,2,3],[3,4,4]]))
sage: t
[[1, 1, 1], [2, 2, 3], [3, 4, 4]]
sage: t.promotion_inverse()
[[1, 1, 2], [2, 3, 3], [4, 4, 4]]
sage: t.promotion_inverse().parent()
The crystal of tableaux of type ['A', 3] and shape(s) [[3, 3, 3]]
Returns the Tableau object corresponding to self.
EXAMPLES:
sage: T = CrystalOfTableaux(['A',3], shape = [2,2])
sage: t = T(rows=[[1,2],[3,4]]).to_tableau(); t
[[1, 2], [3, 4]]
sage: type(t)
<class 'sage.combinat.tableau.Tableau_class'>
sage: type(t[0][0])
<type 'sage.rings.integer.Integer'>
sage: T = CrystalOfTableaux(['D',3], shape = [1,1])
sage: t=T(rows=[[-3],[3]]).to_tableau(); t
[[-3], [3]]
sage: t=T(rows=[[3],[-3]]).to_tableau(); t
[[3], [-3]]
sage: T = CrystalOfTableaux(['B',2], shape = [1,1])
sage: t = T(rows=[[0],[0]]).to_tableau(); t
[[0], [0]]
Bases: sage.structure.unique_representation.UniqueRepresentation, sage.structure.parent.Parent
Auxiliary class to provide a call method to create tensor product elements. This class is shared with several tensor product classes and is also used in CrystalOfTableaux to allow tableaux of different tensor product structures in column-reading (and hence different shapes) to be considered elements in the same crystal.
Bases: sage.combinat.crystals.tensor_product.CrystalOfWords
EXAMPLES:
sage: C = CrystalOfLetters(['A',2])
sage: T = TensorProductOfCrystals(C,C)
sage: T.cardinality()
9
Bases: sage.combinat.combinat.CombinatorialObject, sage.structure.element.Element
A class for lists having a parent
Specification: any subclass C should implement __init__ which accepts the following form C(parent, list = list)
EXAMPLES: We create an immutable list whose parent is the class list:
sage: from sage.combinat.crystals.tensor_product import ImmutableListWithParent, TestParent
sage: l = ImmutableListWithParent(TestParent(), [1,2,3])
sage: l._list
[1, 2, 3]
sage: l.parent()
A parent for tests
sage: l.sibling([2,1]) == ImmutableListWithParent(TestParent(), [2,1])
True
sage: l.reversed()
[3, 2, 1]
sage: l.set_index(1,4)
[1, 4, 3]
Returns the sibling of self which is obtained by reversing the elements of self.
EXAMPLES:
sage: from sage.combinat.crystals.tensor_product import ImmutableListWithParent, TestParent
sage: l = ImmutableListWithParent(TestParent(), [1,2,3])
sage: l.reversed()
[3, 2, 1]
Returns the sibling of self obtained by setting the
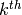 entry of self to value.
entry of self to value.
EXAMPLES:
sage: from sage.combinat.crystals.tensor_product import ImmutableListWithParent, TestParent
sage: l = ImmutableListWithParent(TestParent(), [1,2,3])
sage: l.set_index(0,2)
[2, 2, 3]
sage: l.set_index(1,4)
[1, 4, 3]
sage: _.parent()
A parent for tests
Returns an ImmutableListWithParent object whose list is l and whose parent is the same as self’s parent.
Note that the implementation of this function makes an assumption about the constructor for subclasses.
EXAMPLES:
sage: from sage.combinat.crystals.tensor_product import ImmutableListWithParent, TestParent
sage: l = ImmutableListWithParent(TestParent(), [1,2,3])
sage: m = l.sibling([2,3,4]); m
[2, 3, 4]
sage: m.parent()
A parent for tests
Tensor product of crystals.
Given two crystals  and
and 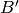 of the same type,
one can form the tensor product
of the same type,
one can form the tensor product 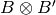 . As a set
. As a set
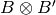 is the Cartesian product
is the Cartesian product
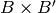 . The crystal operators
. The crystal operators 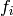 and
and
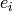 act on
act on 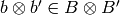 as
follows:
as
follows:
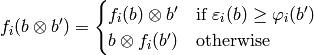
and
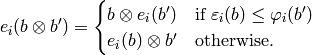
Note that this is the opposite of Kashiwara’s convention for tensor products of crystals.
EXAMPLES:
We construct the type 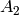 -crystal generated by
-crystal generated by 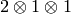 :
:
sage: C = CrystalOfLetters(['A',2])
sage: T = TensorProductOfCrystals(C,C,C,generators=[[C(2),C(1),C(1)]])
It has 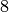 elements:
elements:
sage: T.list()
[[2, 1, 1], [2, 1, 2], [2, 1, 3], [3, 1, 3], [3, 2, 3], [3, 1, 1], [3, 1, 2], [3, 2, 2]]
One can also check the Cartan type of the crystal:
sage: T.cartan_type()
['A', 2]
Other examples include crystals of tableaux (which internally are represented as tensor products obtained by reading the tableaux columnwise):
sage: C = CrystalOfTableaux(['A',3], shape=[1,1,0])
sage: D = CrystalOfTableaux(['A',3], shape=[1,0,0])
sage: T = TensorProductOfCrystals(C,D, generators=[[C(rows=[[1], [2]]), D(rows=[[1]])], [C(rows=[[2], [3]]), D(rows=[[1]])]])
sage: T.cardinality()
24
sage: TestSuite(T).run()
sage: T.module_generators
[[[[1], [2]], [[1]]], [[[2], [3]], [[1]]]]
sage: [x.weight() for x in T.module_generators]
[(2, 1, 0, 0), (1, 1, 1, 0)]
If no module generators are specified, we obtain the full tensor product:
sage: C=CrystalOfLetters(['A',2])
sage: T=TensorProductOfCrystals(C,C)
sage: T.list()
[[1, 1], [1, 2], [1, 3], [2, 1], [2, 2], [2, 3], [3, 1], [3, 2], [3, 3]]
sage: T.cardinality()
9
For a tensor product of crystals without module generators, the default implementation of module_generators contains all elements in the tensor product of the crystals. If there is a subset of elements in the tensor product that still generates the crystal, this needs to be implemented for the specific crystal separately:
sage: T.module_generators.list()
[[1, 1], [1, 2], [1, 3], [2, 1], [2, 2], [2, 3], [3, 1], [3, 2], [3, 3]]
For classical highest weight crystals, it is also possible to list all highest weight elements:
sage: C = CrystalOfLetters(['A',2])
sage: T = TensorProductOfCrystals(C,C,C,generators=[[C(2),C(1),C(1)],[C(1),C(2),C(1)]])
sage: T.highest_weight_vectors()
[[2, 1, 1], [1, 2, 1]]
Bases: sage.combinat.crystals.tensor_product.ImmutableListWithParent
A class for elements of tensor products of crystals
Returns the action of 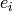 on self.
on self.
EXAMPLES:
sage: C = CrystalOfLetters(['A',5])
sage: T = TensorProductOfCrystals(C,C)
sage: T(C(1),C(2)).e(1) == T(C(1),C(1))
True
sage: T(C(2),C(1)).e(1) == None
True
sage: T(C(2),C(2)).e(1) == T(C(1),C(2))
True
EXAMPLES:
sage: C = CrystalOfLetters(['A',5])
sage: T = TensorProductOfCrystals(C,C)
sage: T(C(1),C(1)).epsilon(1)
0
sage: T(C(1),C(2)).epsilon(1)
1
sage: T(C(2),C(1)).epsilon(1)
0
Returns the action of 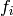 on self.
on self.
EXAMPLES:
sage: C = CrystalOfLetters(['A',5])
sage: T = TensorProductOfCrystals(C,C)
sage: T(C(1),C(1)).f(1)
[1, 2]
sage: T(C(1),C(2)).f(1)
[2, 2]
sage: T(C(2),C(1)).f(1) is None
True
EXAMPLES:
sage: C = CrystalOfLetters(['A',5])
sage: T = TensorProductOfCrystals(C,C)
sage: T(C(1),C(1)).phi(1)
2
sage: T(C(1),C(2)).phi(1)
1
sage: T(C(2),C(1)).phi(1)
0
EXAMPLES:
sage: C = CrystalOfLetters(['A',5])
sage: T = TensorProductOfCrystals(C,C)
sage: T(C(2),C(1)).positions_of_unmatched_minus(1)
[]
sage: T(C(1),C(2)).positions_of_unmatched_minus(1)
[0]
EXAMPLES:
sage: C = CrystalOfLetters(['A',5])
sage: T = TensorProductOfCrystals(C,C)
sage: T(C(2),C(1)).positions_of_unmatched_plus(1)
[]
sage: T(C(1),C(2)).positions_of_unmatched_plus(1)
[1]
Returns the weight of self.
EXAMPLES:
sage: C = CrystalOfLetters(['A',3])
sage: T = TensorProductOfCrystals(C,C)
sage: T(C(1),C(2)).weight()
(1, 1, 0, 0)
sage: T=CrystalOfTableaux(['D',4],shape=[])
sage: T.list()[0].weight()
(0, 0, 0, 0)