Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Combinatorics »
AUTHORS:
This module implements some combinatorial functions, as listed below. For a more detailed description, see the relevant docstrings.
Sequences:
Set-theoretic constructions:
Partitions:
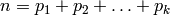 of positive integers and is
represented by the list
of positive integers and is
represented by the list ![p = [p_1,p_2,\ldots,p_k]](../../_images/math/5a7ae185b982284bb0098dcb16f5deac9a6e0216.png) , in
nonincreasing order, i.e.,
, in
nonincreasing order, i.e., 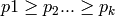 .
.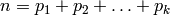 of positive integers and is
represented by the list
of positive integers and is
represented by the list ![p = [p_1,p_2,\ldots,p_k]](../../_images/math/5a7ae185b982284bb0098dcb16f5deac9a6e0216.png) , in
nonincreasing order, i.e.,
, in
nonincreasing order, i.e., 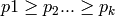 .
.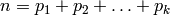 of positive integers
of positive integers
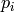 belonging to a given set
belonging to a given set 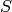 , and is
represented by the list
, and is
represented by the list ![p = [p_1,p_2,\ldots,p_k]](../../_images/math/5a7ae185b982284bb0098dcb16f5deac9a6e0216.png) , in
nonincreasing order, i.e.,
, in
nonincreasing order, i.e., 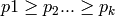 .
. -tuple
of partitions is represented by a list of all
-tuple
of partitions is represented by a list of all  -tuples of
partitions which together form a partition of
-tuples of
partitions which together form a partition of  .
. -th power of
a permutation with cycle structure
-th power of
a permutation with cycle structure  .
. .
.Related functions:
Implemented in other modules (listed for completeness):
The sage.rings.arith module contains the following combinatorial functions:
 .
.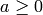 we have
we have 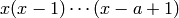 . In all
other cases we use the GAMMA-function:
. In all
other cases we use the GAMMA-function:
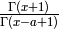 .
.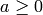 we have
we have 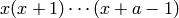 . In all
other cases we use the GAMMA-function:
. In all
other cases we use the GAMMA-function:
 .
.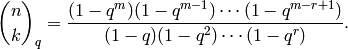
The sage.groups.perm_gps.permgroup_elements contains the following combinatorial functions:
TODO:
GUAVA commands:
* MOLS returns a list of n Mutually Orthogonal Latin Squares (MOLS).
* VandermondeMat
* GrayMat returns a list of all different vectors of length n over
the field F, using Gray ordering.
Not in GAP:
* Rencontres numbers
http://en.wikipedia.org/wiki/Rencontres_number
REFERENCES:
Bases: sage.structure.parent.Parent
This class is deprecated, and will disappear as soon as all derived classes in Sage’s library will have been fixed. Please derive directly from Parent and use the category EnumeratedSets, FiniteEnumeratedSets, or InfiniteEnumeratedSets, as appropriate.
For examples, see:
sage: FiniteEnumeratedSets().example()
An example of a finite enumerated set: {1,2,3}
sage: InfiniteEnumeratedSets().example()
An example of an infinite enumerated set: the non negative integers
Default implementation of cardinality which just goes through the iterator of the combinatorial class to count the number of objects.
EXAMPLES:
sage: class C(CombinatorialClass):
... def __iter__(self):
... return iter([1,2,3])
...
sage: C().cardinality() #indirect doctest
3
Deprecated ! Please use .cardinality instead.
TEST:
sage: class C(CombinatorialClass):
... def __iter__(self):
... return iter([1,2,3])
...
sage: C().count() #indirect doctest
doctest:1: DeprecationWarning: The usage of count for combinatorial classes is deprecated. Please use cardinality
3
This function is a temporary helper so that a CombinatorialClass behaves as a parent for creating elements. This will disappear when combinatorial classes will be turned into actual parents (in the category EnumeratedSets).
TESTS:
sage: P5 = Partitions(5)
sage: P5.element_class
<class 'sage.combinat.partition.Partition_class'>
Returns the combinatorial subclass of f which consists of the elements x of self such that f(x) is True.
EXAMPLES:
sage: P = Permutations(3).filter(lambda x: x.avoids([1,2]))
sage: P.list()
[[3, 2, 1]]
Default implementation for first which uses iterator.
EXAMPLES:
sage: C = CombinatorialClass()
sage: C.list = lambda: [1,2,3]
sage: C.first() # indirect doctest
1
Returns whether self is finite or not.
EXAMPLES:
sage: Partitions(5).is_finite()
True
sage: Permutations().is_finite()
False
Iterator is deprecated for combinatorial classes.
EXAMPLES:
sage: p5 = Partitions(3)
sage: it = p5.iterator()
doctest:1: DeprecationWarning: The usage of iterator for combinatorial classes is deprecated. Please use the class itself
sage: [i for i in it]
[[3], [2, 1], [1, 1, 1]]
sage: [i for i in p5]
[[3], [2, 1], [1, 1, 1]]
Default implementation for first which uses iterator.
EXAMPLES:
sage: C = CombinatorialClass()
sage: C.list = lambda: [1,2,3]
sage: C.last() # indirect doctest
3
The default implementation of list which builds the list from the iterator.
EXAMPLES:
sage: class C(CombinatorialClass):
... def __iter__(self):
... return iter([1,2,3])
...
sage: C().list() #indirect doctest
[1, 2, 3]
Returns the image 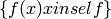 of this combinatorial
class by
of this combinatorial
class by 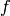 , as a combinatorial class.
, as a combinatorial class.
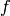 is supposed to be injective.
is supposed to be injective.
EXAMPLES:
sage: R = Permutations(3).map(attrcall('reduced_word')); R
Image of Standard permutations of 3 by *.reduced_word()
sage: R.cardinality()
6
sage: R.list()
[[], [2], [1], [1, 2], [2, 1], [2, 1, 2]]
sage: [ r for r in R]
[[], [2], [1], [1, 2], [2, 1], [2, 1, 2]]
If the function is not injective, then there may be repeated elements:
sage: P = Partitions(4)
sage: P.list()
[[4], [3, 1], [2, 2], [2, 1, 1], [1, 1, 1, 1]]
sage: P.map(len).list()
[1, 2, 2, 3, 4]
TESTS:
sage: R = Permutations(3).map(attrcall('reduced_word'))
sage: R == loads(dumps(R))
True
Default implementation for next which uses iterator.
EXAMPLES:
sage: C = CombinatorialClass()
sage: C.list = lambda: [1,2,3]
sage: C.next(2) # indirect doctest
3
Default implementation for next which uses iterator.
EXAMPLES:
sage: C = CombinatorialClass()
sage: C.list = lambda: [1,2,3]
sage: C.previous(2) # indirect doctest
1
Deprecated. Use self.random_element() instead.
EXAMPLES:
sage: C = CombinatorialClass()
sage: C.random()
...
NotImplementedError: Deprecated: use random_element() instead
Default implementation of random which uses unrank.
EXAMPLES:
sage: C = CombinatorialClass()
sage: C.list = lambda: [1,2,3]
sage: C.random_element() # indirect doctest
1
Default implementation of rank which uses iterator.
EXAMPLES:
sage: C = CombinatorialClass()
sage: C.list = lambda: [1,2,3]
sage: C.rank(3) # indirect doctest
2
Returns the combinatorial class representing the union of self and right_cc.
EXAMPLES:
sage: P = Permutations(2).union(Permutations(1))
sage: P.list()
[[1, 2], [2, 1], [1]]
Default implementation of unrank which goes through the iterator.
EXAMPLES:
sage: C = CombinatorialClass()
sage: C.list = lambda: [1,2,3]
sage: C.unrank(1) # indirect doctest
2
Bases: sage.structure.sage_object.SageObject
EXAMPLES:
sage: c = CombinatorialObject([1,2,3])
sage: c.index(1)
0
sage: c.index(3)
2
Bases: sage.combinat.combinat.CombinatorialClass
EXAMPLES:
sage: P = Permutations(3).filter(lambda x: x.avoids([1,2]))
sage: P.cardinality()
1
Bases: sage.combinat.combinat.CombinatorialClass
This is an internal class that should not be used directly. A class which inherits from InfiniteAbstractCombinatorialClass inherits the standard methods list and count.
If self._infinite_cclass_slice exists then self.__iter__ returns an iterator for self, otherwise raise NotImplementedError. The method self._infinite_cclass_slice is supposed to accept any integer as an argument and return something which is iterable.
Counts the elements of the combinatorial class.
Returns an error since self is an infinite combinatorial class.
Bases: sage.combinat.combinat.CombinatorialClass
A MapCombinatorialClass models the image of a combinatorial class through a function which is assumed to be injective
See CombinatorialClass.map for examples
Returns the cardinality of this combinatorial class
EXAMPLES:
sage: R = Permutations(10).map(attrcall('reduced_word'))
sage: R.cardinality()
3628800
Bases: sage.combinat.combinat.CombinatorialClass
EXAMPLES:
sage: P = Permutations(3).union(Permutations(2))
sage: P.cardinality()
8
EXAMPLES:
sage: P = Permutations(3).union(Permutations(2))
sage: P.first()
[1, 2, 3]
EXAMPLES:
sage: P = Permutations(3).union(Permutations(2))
sage: P.last()
[2, 1]
EXAMPLES:
sage: P = Permutations(3).union(Permutations(2))
sage: P.list()
[[1, 2, 3],
[1, 3, 2],
[2, 1, 3],
[2, 3, 1],
[3, 1, 2],
[3, 2, 1],
[1, 2],
[2, 1]]
EXAMPLES:
sage: P = Permutations(3).union(Permutations(2))
sage: P.rank(Permutation([2,1]))
7
sage: P.rank(Permutation([1,2,3]))
0
EXAMPLES:
sage: P = Permutations(3).union(Permutations(2))
sage: P.unrank(7)
[2, 1]
sage: P.unrank(0)
[1, 2, 3]
An arrangement of mset is an ordered selection without repetitions and is represented by a list that contains only elements from mset, but maybe in a different order.
arrangements returns the set of arrangements of the multiset mset that contain k elements.
IMPLEMENTATION: Wraps GAP’s Arrangements.
Warning
Wraps GAP - hence mset must be a list of objects that have string representations that can be interpreted by the GAP interpreter. If mset consists of at all complicated Sage objects, this function does not do what you expect. A proper function should be written! (TODO!)
EXAMPLES:
sage: mset = [1,1,2,3,4,4,5]
sage: arrangements(mset,2)
[[1, 1],
[1, 2],
[1, 3],
[1, 4],
[1, 5],
[2, 1],
[2, 3],
[2, 4],
[2, 5],
[3, 1],
[3, 2],
[3, 4],
[3, 5],
[4, 1],
[4, 2],
[4, 3],
[4, 4],
[4, 5],
[5, 1],
[5, 2],
[5, 3],
[5, 4]]
sage: arrangements( ["c","a","t"], 2 )
['ac', 'at', 'ca', 'ct', 'ta', 'tc']
sage: arrangements( ["c","a","t"], 3 )
['act', 'atc', 'cat', 'cta', 'tac', 'tca']
Returns the n-th Bell number (the number of ways to partition a set of n elements into pairwise disjoint nonempty subsets).
If 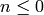 , returns
, returns  .
.
Wraps GAP’s Bell.
EXAMPLES:
sage: bell_number(10)
115975
sage: bell_number(2)
2
sage: bell_number(-10)
1
sage: bell_number(1)
1
sage: bell_number(1/3)
...
TypeError: no conversion of this rational to integer
This function returns the Bell Polynomial
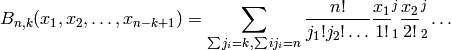
INPUT:
OUTPUT:
EXAMPLES:
sage: bell_polynomial(6,2)
10*x_3^2 + 15*x_2*x_4 + 6*x_1*x_5
sage: bell_polynomial(6,3)
15*x_2^3 + 60*x_1*x_2*x_3 + 15*x_1^2*x_4
REFERENCES:
AUTHORS:
Return the nth Bernoulli polynomial as a polynomial in x. In particular, if x is anything other than a variable, this will simply be the nth Bernoulli polynomial evaluated at x.
The generating function for the Bernoulli polynomials is
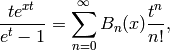
and they are given directly by
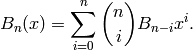
One has 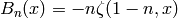 , where
, where
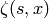 is the Hurwitz zeta function. Thus, in a
certain sense, the Hurwitz zeta generalizes the Bernoulli
polynomials to non-integer values of n.
is the Hurwitz zeta function. Thus, in a
certain sense, the Hurwitz zeta generalizes the Bernoulli
polynomials to non-integer values of n.
EXAMPLES:
sage: y = QQ['y'].0
sage: bernoulli_polynomial(y,5)
y^5 - 5/2*y^4 + 5/3*y^3 - 1/6*y
sage: bernoulli_polynomial(y,5)(12)
199870
sage: bernoulli_polynomial(12,5)
199870
REFERENCES:
Returns the n-th Catalan number
Catalan numbers: The  -th Catalan number is given
directly in terms of binomial coefficients by
-th Catalan number is given
directly in terms of binomial coefficients by
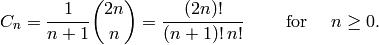
Consider the set 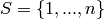 . A noncrossing
partition of
. A noncrossing
partition of 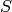 is a partition in which no two blocks
“cross” each other, i.e., if a and b belong to one block and x and
y to another, they are not arranged in the order axby.
is a partition in which no two blocks
“cross” each other, i.e., if a and b belong to one block and x and
y to another, they are not arranged in the order axby.
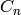 is the number of noncrossing partitions of the set
is the number of noncrossing partitions of the set
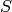 . There are many other interpretations (see
REFERENCES).
. There are many other interpretations (see
REFERENCES).
When 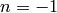 , this function raises a ZeroDivisionError; for
other
, this function raises a ZeroDivisionError; for
other 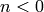 it returns
it returns 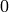 .
.
INPUT:
OUTPUT: integer
EXAMPLES:
sage: [catalan_number(i) for i in range(7)]
[1, 1, 2, 5, 14, 42, 132]
sage: taylor((-1/2)*sqrt(1 - 4*x^2), x, 0, 15)
132*x^14 + 42*x^12 + 14*x^10 + 5*x^8 + 2*x^6 + x^4 + x^2 - 1/2
sage: [catalan_number(i) for i in range(-7,7) if i != -1]
[0, 0, 0, 0, 0, 0, 1, 1, 2, 5, 14, 42, 132]
sage: catalan_number(-1)
...
ZeroDivisionError
sage: [catalan_number(n).mod(2) for n in range(16)]
[1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1]
REFERENCES:
A combination of a multiset (a list of objects which may contain the same object several times) mset is an unordered selection without repetitions and is represented by a sorted sublist of mset. Returns the set of all combinations of the multiset mset with k elements.
Warning
Wraps GAP’s Combinations. Hence mset must be a list of objects that have string representations that can be interpreted by the GAP interpreter. If mset consists of at all complicated Sage objects, this function does not do what you expect. A proper function should be written! (TODO!)
EXAMPLES:
sage: mset = [1,1,2,3,4,4,5]
sage: combinations(mset,2)
[[1, 1],
[1, 2],
[1, 3],
[1, 4],
[1, 5],
[2, 3],
[2, 4],
[2, 5],
[3, 4],
[3, 5],
[4, 4],
[4, 5]]
sage: mset = ["d","a","v","i","d"]
sage: combinations(mset,3)
['add', 'adi', 'adv', 'aiv', 'ddi', 'ddv', 'div']
Note
For large lists, this raises a string error.
Posted by Raymond Hettinger, 2006/03/23, to the Python Cookbook: http://aspn.activestate.com/ASPN/Cookbook/Python/Recipe/474124
Much faster than combinations.
EXAMPLES:
sage: X = combinations_iterator([1,2,3,4,5],3)
sage: [x for x in X]
[[1, 2, 3],
[1, 2, 4],
[1, 2, 5],
[1, 3, 4],
[1, 3, 5],
[1, 4, 5],
[2, 3, 4],
[2, 3, 5],
[2, 4, 5],
[3, 4, 5]]
Returns a list of all cyclic permutations of mset. Treats mset as a list, not a set, i.e. entries with the same value are distinct.
AUTHORS:
EXAMPLES:
sage: from sage.combinat.combinat import cyclic_permutations, cyclic_permutations_iterator
sage: cyclic_permutations(range(4))
[[0, 1, 2, 3], [0, 1, 3, 2], [0, 2, 1, 3], [0, 2, 3, 1], [0, 3, 1, 2], [0, 3, 2, 1]]
sage: for cycle in cyclic_permutations(['a', 'b', 'c']):
... print cycle
['a', 'b', 'c']
['a', 'c', 'b']
Note that lists with repeats are not handled intuitively:
sage: cyclic_permutations([1,1,1])
[[1, 1, 1], [1, 1, 1]]
Iterates over all cyclic permutations of mset in cycle notation. Treats mset as a list, not a set, i.e. entries with the same value are distinct.
AUTHORS:
EXAMPLES:
sage: from sage.combinat.combinat import cyclic_permutations, cyclic_permutations_iterator
sage: cyclic_permutations(range(4))
[[0, 1, 2, 3], [0, 1, 3, 2], [0, 2, 1, 3], [0, 2, 3, 1], [0, 3, 1, 2], [0, 3, 2, 1]]
sage: for cycle in cyclic_permutations(['a', 'b', 'c']):
... print cycle
['a', 'b', 'c']
['a', 'c', 'b']
Note that lists with repeats are not handled intuitively:
sage: cyclic_permutations([1,1,1])
[[1, 1, 1], [1, 1, 1]]
A derangement is a fixed point free permutation of list and is represented by a list that contains exactly the same elements as mset, but possibly in different order. Derangements returns the set of all derangements of a multiset.
Wraps GAP’s Derangements.
Warning
Wraps GAP - hence mset must be a list of objects that have string representations that can be interpreted by the GAP interpreter. If mset consists of at all complicated Sage objects, this function does not do what you expect. A proper function should be written! (TODO!)
EXAMPLES:
sage: mset = [1,2,3,4]
sage: derangements(mset)
[[2, 1, 4, 3],
[2, 3, 4, 1],
[2, 4, 1, 3],
[3, 1, 4, 2],
[3, 4, 1, 2],
[3, 4, 2, 1],
[4, 1, 2, 3],
[4, 3, 1, 2],
[4, 3, 2, 1]]
sage: derangements(["c","a","t"])
['atc', 'tca']
Returns the n-th Euler number
IMPLEMENTATION: Wraps Maxima’s euler.
EXAMPLES:
sage: [euler_number(i) for i in range(10)]
[1, 0, -1, 0, 5, 0, -61, 0, 1385, 0]
sage: maxima.eval("taylor (2/(exp(x)+exp(-x)), x, 0, 10)")
'1-x^2/2+5*x^4/24-61*x^6/720+277*x^8/8064-50521*x^10/3628800'
sage: [euler_number(i)/factorial(i) for i in range(11)]
[1, 0, -1/2, 0, 5/24, 0, -61/720, 0, 277/8064, 0, -50521/3628800]
sage: euler_number(-1)
...
ValueError: n (=-1) must be a nonnegative integer
REFERENCES:
Returns the n-th Fibonacci number. The Fibonacci sequence
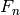 is defined by the initial conditions
is defined by the initial conditions
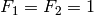 and the recurrence relation
and the recurrence relation
 . For negative
. For negative  we
define
we
define 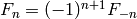 , which is consistent with
the recurrence relation.
, which is consistent with
the recurrence relation.
INPUT:
Note
PARI is tens to hundreds of times faster than GAP here; moreover, PARI works for every large input whereas GAP doesn’t.
EXAMPLES:
sage: fibonacci(10)
55
sage: fibonacci(10, algorithm='gap')
55
sage: fibonacci(-100)
-354224848179261915075
sage: fibonacci(100)
354224848179261915075
sage: fibonacci(0)
0
sage: fibonacci(1/2)
...
TypeError: no conversion of this rational to integer
Returns an iterator over the Fibonacci sequence, for all fibonacci
numbers 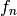 from n = start up to (but
not including) n = stop
from n = start up to (but
not including) n = stop
INPUT:
EXAMPLES:
sage: fibs = [i for i in fibonacci_sequence(10, 20)]
sage: fibs
[55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181]
sage: sum([i for i in fibonacci_sequence(100, 110)])
69919376923075308730013
See also
AUTHORS:
Returns an iterator over all of the Fibonacci numbers in the given range, including f_n = start up to, but not including, f_n = stop.
EXAMPLES:
sage: fibs_in_some_range = [i for i in fibonacci_xrange(10^7, 10^8)]
sage: len(fibs_in_some_range)
4
sage: fibs_in_some_range
[14930352, 24157817, 39088169, 63245986]
sage: fibs = [i for i in fibonacci_xrange(10, 100)]
sage: fibs
[13, 21, 34, 55, 89]
sage: list(fibonacci_xrange(13, 34))
[13, 21]
A solution to the second Project Euler problem:
sage: sum([i for i in fibonacci_xrange(10^6) if is_even(i)])
1089154
See also
AUTHORS:
Returns the value of the 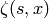 to
to  decimals, where s and x are real.
decimals, where s and x are real.
The Hurwitz zeta function is one of the many zeta functions. It defined as
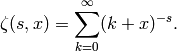
When 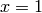 , this coincides with Riemann’s zeta function.
The Dirichlet L-functions may be expressed as a linear combination
of Hurwitz zeta functions.
, this coincides with Riemann’s zeta function.
The Dirichlet L-functions may be expressed as a linear combination
of Hurwitz zeta functions.
Note that if you use floating point inputs, then the results may be slightly off.
EXAMPLES:
sage: hurwitz_zeta(3,1/2,6)
8.41439000000000
sage: hurwitz_zeta(11/10,1/2,6)
12.1041000000000
sage: hurwitz_zeta(11/10,1/2,50)
12.10381349568375510570907741296668061903364861809
REFERENCES:
Returns the n-th Lucas number “of the first kind” (this is not
standard terminology). The Lucas sequence 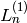 is
defined by the initial conditions
is
defined by the initial conditions 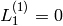 ,
,
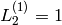 and the recurrence relation
and the recurrence relation
 .
.
Wraps GAP’s Lucas(...)[1].
P=1, Q=-1 gives the Fibonacci sequence.
INPUT:
OUTPUT: integer or rational number
EXAMPLES:
sage: lucas_number1(5,1,-1)
5
sage: lucas_number1(6,1,-1)
8
sage: lucas_number1(7,1,-1)
13
sage: lucas_number1(7,1,-2)
43
sage: lucas_number1(5,2,3/5)
229/25
sage: lucas_number1(5,2,1.5)
...
TypeError: no canonical coercion from Real Field with 53 bits of precision to Rational Field
There was a conjecture that the sequence 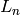 defined by
defined by
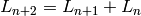 ,
, 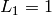 ,
,
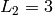 , has the property that
, has the property that  prime implies
that
prime implies
that 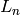 is prime.
is prime.
sage: lucas = lambda n : Integer((5/2)*lucas_number1(n,1,-1)+(1/2)*lucas_number2(n,1,-1))
sage: [[lucas(n),is_prime(lucas(n)),n+1,is_prime(n+1)] for n in range(15)]
[[1, False, 1, False],
[3, True, 2, True],
[4, False, 3, True],
[7, True, 4, False],
[11, True, 5, True],
[18, False, 6, False],
[29, True, 7, True],
[47, True, 8, False],
[76, False, 9, False],
[123, False, 10, False],
[199, True, 11, True],
[322, False, 12, False],
[521, True, 13, True],
[843, False, 14, False],
[1364, False, 15, False]]
Can you use Sage to find a counterexample to the conjecture?
Returns the n-th Lucas number “of the second kind” (this is not
standard terminology). The Lucas sequence 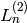 is
defined by the initial conditions
is
defined by the initial conditions 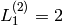 ,
,
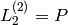 and the recurrence relation
and the recurrence relation
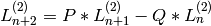 .
.
Wraps GAP’s Lucas(...)[2].
INPUT:
OUTPUT: integer or rational number
EXAMPLES:
sage: [lucas_number2(i,1,-1) for i in range(10)]
[2, 1, 3, 4, 7, 11, 18, 29, 47, 76]
sage: [fibonacci(i-1)+fibonacci(i+1) for i in range(10)]
[2, 1, 3, 4, 7, 11, 18, 29, 47, 76]
sage: n = lucas_number2(5,2,3); n
2
sage: type(n)
<type 'sage.rings.integer.Integer'>
sage: n = lucas_number2(5,2,-3/9); n
418/9
sage: type(n)
<type 'sage.rings.rational.Rational'>
The case P=1, Q=-1 is the Lucas sequence in Brualdi’s Introductory Combinatorics, 4th ed., Prentice-Hall, 2004:
sage: [lucas_number2(n,1,-1) for n in range(10)]
[2, 1, 3, 4, 7, 11, 18, 29, 47, 76]
Returns the size of arrangements(mset,k). Wraps GAP’s NrArrangements.
EXAMPLES:
sage: mset = [1,1,2,3,4,4,5]
sage: number_of_arrangements(mset,2)
22
Returns the size of combinations(mset,k). IMPLEMENTATION: Wraps GAP’s NrCombinations.
Note
mset must be a list of integers or strings (i.e., this is very restricted).
EXAMPLES:
sage: mset = [1,1,2,3,4,4,5]
sage: number_of_combinations(mset,2)
12
Returns the size of derangements(mset). Wraps GAP’s NrDerangements.
EXAMPLES:
sage: mset = [1,2,3,4]
sage: number_of_derangements(mset)
9
Do not use this function. It will be deprecated in future version of Sage and eventually removed. Use Permutations instead; instead of
number_of_permutations(mset)
use
Permutations(mset).cardinality().
If you insist on using this now:
Returns the size of permutations(mset).
AUTHORS:
EXAMPLES:
sage: mset = [1,1,2,2,2]
sage: number_of_permutations(mset)
10
Returns the size of tuples(S,k). Wraps GAP’s NrTuples.
EXAMPLES:
sage: S = [1,2,3,4,5]
sage: number_of_tuples(S,2)
25
sage: S = [1,1,2,3,4,5]
sage: number_of_tuples(S,2)
25
Returns the size of unordered_tuples(S,k). Wraps GAP’s NrUnorderedTuples.
EXAMPLES:
sage: S = [1,2,3,4,5]
sage: number_of_unordered_tuples(S,2)
15
A permutation is represented by a list that contains exactly the
same elements as mset, but possibly in different order. If mset is
a proper set there are 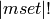 such permutations.
Otherwise if the first elements appears
such permutations.
Otherwise if the first elements appears 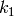 times, the
second element appears
times, the
second element appears 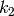 times and so on, the number
of permutations is
times and so on, the number
of permutations is 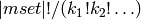 , which
is sometimes called a multinomial coefficient.
, which
is sometimes called a multinomial coefficient.
permutations returns the set of all permutations of a multiset. Calls a function written by Mike Hansen, not GAP.
EXAMPLES:
sage: mset = [1,1,2,2,2]
sage: permutations(mset)
[[1, 1, 2, 2, 2],
[1, 2, 1, 2, 2],
[1, 2, 2, 1, 2],
[1, 2, 2, 2, 1],
[2, 1, 1, 2, 2],
[2, 1, 2, 1, 2],
[2, 1, 2, 2, 1],
[2, 2, 1, 1, 2],
[2, 2, 1, 2, 1],
[2, 2, 2, 1, 1]]
sage: MS = MatrixSpace(GF(2),2,2)
sage: A = MS([1,0,1,1])
sage: permutations(A.rows())
[[(1, 0), (1, 1)], [(1, 1), (1, 0)]]
Do not use this function. It will be deprecated in future version of Sage and eventually removed. Use Permutations instead; instead of
for p in permutations_iterator(range(1, m+1), n)
use
for p in Permutations(m, n).
Note that Permutations, unlike this function, treats repeated elements as identical.
If you insist on using this now:
Returns an iterator (http://docs.python.org/lib/typeiter.html) which can be used in place of permutations(mset) if all you need it for is a ‘for’ loop.
Posted by Raymond Hettinger, 2006/03/23, to the Python Cookbook: http://aspn.activestate.com/ASPN/Cookbook/Python/Recipe/474124
Note- This function considers repeated elements as different entries, so for example:
sage: from sage.combinat.combinat import permutations, permutations_iterator
sage: mset = [1,2,2]
sage: permutations(mset)
[[1, 2, 2], [2, 1, 2], [2, 2, 1]]
sage: for p in permutations_iterator(mset): print p
[1, 2, 2]
[1, 2, 2]
[2, 1, 2]
[2, 2, 1]
[2, 1, 2]
[2, 2, 1]
EXAMPLES:
sage: X = permutations_iterator(range(3),2)
sage: [x for x in X]
[[0, 1], [0, 2], [1, 0], [1, 2], [2, 0], [2, 1]]
Returns the n-th Stilling number 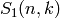 of the first
kind (the number of permutations of n points with k cycles). Wraps
GAP’s Stirling1.
of the first
kind (the number of permutations of n points with k cycles). Wraps
GAP’s Stirling1.
EXAMPLES:
sage: stirling_number1(3,2)
3
sage: stirling_number1(5,2)
50
sage: 9*stirling_number1(9,5)+stirling_number1(9,4)
269325
sage: stirling_number1(10,5)
269325
Indeed, 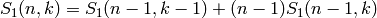 .
.
Returns the n-th Stirling number 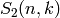 of the second
kind (the number of ways to partition a set of n elements into k
pairwise disjoint nonempty subsets). (The n-th Bell number is the
sum of the
of the second
kind (the number of ways to partition a set of n elements into k
pairwise disjoint nonempty subsets). (The n-th Bell number is the
sum of the 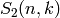 ‘s,
‘s, 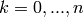 .) Wraps GAP’s
Stirling2.
.) Wraps GAP’s
Stirling2.
EXAMPLES: Stirling numbers satisfy
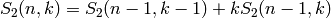 :
:
sage: 5*stirling_number2(9,5) + stirling_number2(9,4)
42525
sage: stirling_number2(10,5)
42525
sage: n = stirling_number2(20,11); n
1900842429486
sage: type(n)
<type 'sage.rings.integer.Integer'>
An ordered tuple of length k of set is an ordered selection with repetition and is represented by a list of length k containing elements of set. tuples returns the set of all ordered tuples of length k of the set.
EXAMPLES:
sage: S = [1,2]
sage: tuples(S,3)
[[1, 1, 1], [2, 1, 1], [1, 2, 1], [2, 2, 1], [1, 1, 2], [2, 1, 2], [1, 2, 2], [2, 2, 2]]
sage: mset = ["s","t","e","i","n"]
sage: tuples(mset,2)
[['s', 's'], ['t', 's'], ['e', 's'], ['i', 's'], ['n', 's'], ['s', 't'], ['t', 't'],
['e', 't'], ['i', 't'], ['n', 't'], ['s', 'e'], ['t', 'e'], ['e', 'e'], ['i', 'e'],
['n', 'e'], ['s', 'i'], ['t', 'i'], ['e', 'i'], ['i', 'i'], ['n', 'i'], ['s', 'n'],
['t', 'n'], ['e', 'n'], ['i', 'n'], ['n', 'n']]
The Set(...) comparisons are necessary because finite fields are not enumerated in a standard order.
sage: K.<a> = GF(4, 'a')
sage: mset = [x for x in K if x!=0]
sage: tuples(mset,2)
[[a, a], [a + 1, a], [1, a], [a, a + 1], [a + 1, a + 1], [1, a + 1], [a, 1], [a + 1, 1], [1, 1]]
AUTHORS:
An unordered tuple of length k of set is a unordered selection with repetitions of set and is represented by a sorted list of length k containing elements from set.
unordered_tuples returns the set of all unordered tuples of length k of the set. Wraps GAP’s UnorderedTuples.
Warning
Wraps GAP - hence mset must be a list of objects that have string representations that can be interpreted by the GAP interpreter. If mset consists of at all complicated Sage objects, this function does not do what you expect. A proper function should be written! (TODO!)
EXAMPLES:
sage: S = [1,2]
sage: unordered_tuples(S,3)
[[1, 1, 1], [1, 1, 2], [1, 2, 2], [2, 2, 2]]
sage: unordered_tuples(["a","b","c"],2)
['aa', 'ab', 'ac', 'bb', 'bc', 'cc']