AUTHORS:
This is the abstract class hierarchy, i.e., these are all abstract base classes.
SageObject
Element
ModuleElement
RingElement
CommutativeRingElement
IntegralDomainElement
DedekindDomainElement
PrincipalIdealDomainElement
EuclideanDomainElement
FieldElement
FiniteFieldElement
CommutativeAlgebraElement
AlgebraElement (note -- can't derive from module, since no multiple inheritance)
CommutativeAlgebra ??? (should be removed from element.pxd)
Matrix
InfinityElement
PlusInfinityElement
MinusInfinityElement
AdditiveGroupElement
Vector
MonoidElement
MultiplicativeGroupElement
Elements typically define a method _new_c, e.g.,
cdef _new_c(self, defining data):
cdef FreeModuleElement_generic_dense x
x = PY_NEW(FreeModuleElement_generic_dense)
x._parent = self._parent
x._entries = v
that creates a new sibling very quickly from defining data with assumed properties.
Sage has a special system in place for handling arithmetic operations for all Element subclasses. There are various rules that must be followed by both arithmetic implementers and callers.
A quick summary for the impatient:
Now in more detail. The aims of this system are to provide (1) an efficient calling protocol from both Python and Cython, (2) uniform coercion semantics across Sage, (3) ease of use, (4) readability of code.
We will take addition of RingElements as an example; all other operators and classes are similar. There are four relevant functions.
def RingElement.__add__
This function is called by Python or Pyrex when the binary “+” operator is encountered. It ASSUMES that at least one of its arguments is a RingElement; only a really twisted programmer would violate this condition. It has a fast pathway to deal with the most common case where the arguments have the same parent. Otherwise, it uses the coercion module to work out how to make them have the same parent. After any necessary coercions have been performed, it calls _add_ to dispatch to the correct underlying addition implementation.
Note that although this function is declared as def, it doesn’t have the usual overheads associated with python functions (either for the caller or for __add__ itself). This is because python has optimised calling protocols for such special functions.
def RingElement._add_
This is the function you should override to implement addition in a python subclass of RingElement.
Warning
if you override this in a Cython class, it won’t get called. You should override _add_ instead. It is especially important to keep this in mind whenever you move a class down from Python to Cython.
The two arguments to this function are guaranteed to have the SAME PARENT. Its return value MUST have the SAME PARENT as its arguments.
If you want to add two objects from python, and you know that their parents are the same object, you are encouraged to call this function directly, instead of using “x + y”.
The default implementation of this function is to call _add_, so if no-one has defined a python implementation, the correct Pyrex implementation will get called.
cpdef RingElement._add_
This is the function you should override to implement addition in a Pyrex subclass of RingElement.
The two arguments to this function are guaranteed to have the SAME PARENT. Its return value MUST have the SAME PARENT as its arguments.
The default implementation of this function is to raise a NotImplementedError, which will happen if no-one has supplied implementations of either _add_.
For speed, there are also inplace version of the arithmetic commands. DD NOT call them directly, they may mutate the object and will be called when and only when it has been determined that the old object will no longer be accessible from the calling function after this operation.
def RingElement._iadd_
This is the function you should override to inplace implement addition in a Python subclass of RingElement.
The two arguments to this function are guaranteed to have the SAME PARENT. Its return value MUST have the SAME PARENT as its arguments.
The default implementation of this function is to call _add_, so if no-one has defined a Python implementation, the correct Cython implementation will get called.
Bases: sage.structure.element.ModuleElement
Generic element of an additive group.
Bases: object
Most basic coercion scheme. If it doesn’t already match, throw an error.
Bases: sage.structure.element.RingElement
Return True if self divides x.
EXAMPLES:
sage: P.<x> = PolynomialRing(QQ)
sage: x.divides(x^2)
True
sage: x.divides(x^2+2)
False
sage: (x^2+2).divides(x)
False
sage: P.<x> = PolynomialRing(ZZ)
sage: x.divides(x^2)
True
sage: x.divides(x^2+2)
False
sage: (x^2+2).divides(x)
False
Ticket #5347 has been fixed:
sage: K = GF(7)
sage: K(3).divides(1)
True
sage: K(3).divides(K(1))
True
sage: R = Integers(128)
sage: R(0).divides(1)
False
sage: R(0).divides(0)
True
sage: R(0).divides(R(0))
True
sage: R(1).divides(0)
True
sage: R(121).divides(R(120))
True
sage: R(120).divides(R(121))
...
ZeroDivisionError: reduction modulo right not defined.
 , if defined,
i.e., if
, if defined,
i.e., if  and self together generate the unit ideal.
and self together generate the unit ideal.Return a representative for self modulo the ideal I (or the ideal generated by the elements of I if I is not an ideal.)
EXAMPLE: Integers Reduction of 5 modulo an ideal:
sage: n = 5
sage: n.mod(3*ZZ)
2
Reduction of 5 modulo the ideal generated by 3:
sage: n.mod(3)
2
Reduction of 5 modulo the ideal generated by 15 and 6, which is  .
.
sage: n.mod([15,6])
2
EXAMPLE: Univariate polynomials
sage: R.<x> = PolynomialRing(QQ)
sage: f = x^3 + x + 1
sage: f.mod(x + 1)
-1
When little is implemented about a given ring, then mod may
return simply return 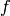 . For example, reduction is not
implemented for
. For example, reduction is not
implemented for ![\ZZ[x]](../../_images/math/997bd738c8f73a5487d82a0af9f18a75a09c06ec.png) yet. (TODO!)
yet. (TODO!)
sage: R.<x> = PolynomialRing(ZZ) sage: f = x^3 + x + 1 sage: f.mod(x + 1) x^3 + x + 1
EXAMPLE: Multivariate polynomials We reduce a polynomial in two variables modulo a polynomial and an ideal:
sage: R.<x,y,z> = PolynomialRing(QQ, 3)
sage: (x^2 + y^2 + z^2).mod(x+y+z)
2*y^2 + 2*y*z + 2*z^2
Notice above that  is eliminated. In the next example,
both
is eliminated. In the next example,
both 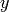 and
and  are eliminated:
are eliminated:
sage: (x^2 + y^2 + z^2).mod( (x - y, y - z) )
3*z^2
sage: f = (x^2 + y^2 + z^2)^2; f
x^4 + 2*x^2*y^2 + y^4 + 2*x^2*z^2 + 2*y^2*z^2 + z^4
sage: f.mod( (x - y, y - z) )
9*z^4
In this example 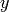 is eliminated:
is eliminated:
sage: (x^2 + y^2 + z^2).mod( (x^3, y - z) )
x^2 + 2*z^2
Bases: sage.structure.sage_object.SageObject
Generic element of a structure. All other types of elements (RingElement, ModuleElement, etc) derive from this type.
Subtypes must either call __init__() to set _parent, or may set _parent themselves if that would be more efficient.
Return True if self equals self.parent()(0). The default implementation is to fall back to ‘not self.__nonzero__’.
Warning
Do not re-implement this method in your subclass but implement __nonzero__ instead.
Return a numerical approximation of x with at least prec bits of precision.
EXAMPLES:
sage: (2/3).n()
0.666666666666667
sage: a = 2/3
sage: pi.n(digits=10)
3.141592654
sage: pi.n(prec=20) # 20 bits
3.1416
Substitutes given generators with given values while not touching other generators. This is a generic wrapper around __call__. The syntax is meant to be compatible with the corresponding method for symbolic expressions.
INPUT:
OUTPUT:
EXAMPLES:
sage: x, y = PolynomialRing(ZZ,2,'xy').gens()
sage: f = x^2 + y + x^2*y^2 + 5
sage: f((5,y))
25*y^2 + y + 30
sage: f.subs({x:5})
25*y^2 + y + 30
sage: f.subs(x=5)
25*y^2 + y + 30
sage: (1/f).subs(x=5)
1/(25*y^2 + y + 30)
sage: Integer(5).subs(x=4)
5
This is an alias for self.subs().
INPUT:
OUTPUT:
EXAMPLES:
sage: x, y = PolynomialRing(ZZ,2,'xy').gens()
sage: f = x^2 + y + x^2*y^2 + 5
sage: f((5,y))
25*y^2 + y + 30
sage: f.substitute({x:5})
25*y^2 + y + 30
sage: f.substitute(x=5)
25*y^2 + y + 30
sage: (1/f).substitute(x=5)
1/(25*y^2 + y + 30)
sage: Integer(5).substitute(x=4)
5
Bases: sage.structure.element.PrincipalIdealDomainElement
Bases: sage.structure.element.CommutativeRingElement
Check whether self divides other, for field elements.
Since this is a field, all values divide all other values, except that zero does not divide any non-zero values.
EXAMPLES:
sage: K.<rt3> = QQ[sqrt(3)]
sage: K(0).divides(rt3)
False
sage: rt3.divides(K(17))
True
sage: K(0).divides(K(0))
True
sage: rt3.divides(K(0))
True
Return True if self is a unit in its parent ring.
EXAMPLES:
sage: a = 2/3; a.is_unit()
True
On the other hand, 2 is not a unit, since its parent is ZZ.
sage: a = 2; a.is_unit()
False
sage: parent(a)
Integer Ring
However, a is a unit when viewed as an element of QQ:
sage: a = QQ(2); a.is_unit()
True
Return the quotient and remainder obtained by dividing 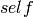 by
by
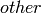 . Since this element lives in a field, the remainder is always
zero and the quotient is
. Since this element lives in a field, the remainder is always
zero and the quotient is  .
.
TESTS:
Test if #8671 is fixed:
sage: R.<x,y> = QQ[]
sage: S.<a,b> = R.quo(y^2 + 1)
sage: S.is_field = lambda : False
sage: F = Frac(S); u = F.one_element()
sage: u.quo_rem(u)
(1, 0)
Bases: sage.structure.element.CommutativeRingElement
Bases: sage.structure.element.Element
Generic element of a module.
Bases: sage.structure.element.Element
Generic element of a monoid.
Bases: sage.structure.element.MonoidElement
Generic element of a multiplicative group.
Bases: object
A decorator to be used on binary operation methods that should operate on elements of the same parent. If the parents of the arguments differ, coercion is performed, then the method is re-looked up by name on the first argument.
In short, using the NamedBinopMethod (alias coerce_binop) decorator on a method gives it the exact same semantics of the basic arithmetic operations like _add_, _sub_, etc. in that both operands are guaranteed to have exactly the same parent.
Bases: sage.structure.element.DedekindDomainElement
Return the extended gcd of self and other, i.e., elements  such that
.. math:
such that
.. math:
r = s \cdot self + t \cdot other.
Note
There is no guarantee on minimality of the cofactors. In the integer case, see documentation for Integer._xgcd() to obtain minimal cofactors.
Bases: sage.structure.element.ModuleElement
Return the absolute value of self. (This just calls the __abs__ method, so it is equivalent to the abs() built-in function.)
EXAMPLES:
sage: RR(-1).abs()
1.00000000000000
sage: ZZ(-1).abs()
1
sage: CC(I).abs()
1.00000000000000
sage: Mod(-15, 37).abs()
...
ArithmeticError: absolute valued not defined on integers modulo n.
Return the additive order of self.
This is deprecated; use additive_order instead.
EXAMPLES:
sage: a = Integers(12)(5)
sage: a.order()
doctest... DeprecationWarning: The function order is deprecated for ring elements; use additive_order or multiplicative_order instead.
12
canonical_coercion(x,y) is what is called before doing an arithmetic operation between x and y. It returns a pair (z,w) such that z is got from x and w from y via canonical coercion and the parents of z and w are identical.
EXAMPLES:
sage: A = Matrix([[0,1],[1,0]])
sage: canonical_coercion(A,1)
(
[0 1] [1 0]
[1 0], [0 1]
)
This function is very helpful in debugging coercion errors. It prints the tracebacks of all the errors caught in the coercion detection. Note that failure is cached, so some errors may be omitted the second time around (as it remembers not to retry failed paths for speed reasons.
EXAMPLES:
sage: 1 + 1/5
6/5
sage: coercion_traceback() # Should be empty, as all went well.
sage: 1/5 + GF(5).gen()
...
TypeError: unsupported operand parent(s) for '+': 'Rational Field' and 'Finite Field of size 5'
sage: coercion_traceback()
...
TypeError: no common canonical parent for objects with parents: 'Rational Field' and 'Finite Field of size 5'
Computes 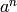 , where
, where  is an integer, and
is an integer, and  is an object which
supports multiplication. Optionally an additional argument,
which is used in the case that n == 0:
is an object which
supports multiplication. Optionally an additional argument,
which is used in the case that n == 0:
If this is not supplied, int(1) is returned.
EXAMPLES:
sage: from sage.structure.element import generic_power
sage: generic_power(int(12),int(0))
1
sage: generic_power(int(0),int(100))
0
sage: generic_power(Integer(10),Integer(0))
1
sage: generic_power(Integer(0),Integer(23))
0
sage: sum([generic_power(2,i) for i in range(17)]) #test all 4-bit combinations
131071
sage: F = Zmod(5)
sage: a = generic_power(F(2), 5); a
2
sage: a.parent() is F
True
sage: a = generic_power(F(1), 2)
sage: a.parent() is F
True
sage: generic_power(int(5), 0)
1
Return the global coercion model.
EXAMPLES:
sage: import sage.structure.element as e
sage: cm = e.get_coercion_model()
sage: cm
<sage.structure.coerce.CoercionModel_cache_maps object at ...>
Return True if x is of type Element.
EXAMPLES:
sage: from sage.structure.element import is_Element
sage: is_Element(2/3)
True
sage: is_Element(QQ^3)
False
Return True if x is of type ModuleElement.
This is even faster than using isinstance inline.
EXAMPLES:
sage: from sage.structure.element import is_ModuleElement
sage: is_ModuleElement(2/3)
True
sage: is_ModuleElement((QQ^3).0)
True
sage: is_ModuleElement('a')
False
This function is only here to support old pickles.
Pickling functionality is moved to Element.{__getstate__,__setstate__} functions.