Spin Crystals¶

These are the crystals associated with the three spin representations: the spin representations of odd orthogonal groups (or rather their double covers); and the + and - spin representations of the even orthogonal groups.

We follow Kashiwara and Nakashima (Journal of Algebra 165, 1994) in representing the elements of the spin Crystal by sequences of signs +/-. Two other representations are available as attributes internal_repn and signature of the crystal element.

A numerical internal representation, an integer N such that if N-1 is written in binary and the 1’s are replaced by -, the 0’s by +
The signature, which is a list in which + is replaced by +1 and - by -1.

sage.combinat.crystals.spins.CrystalOfSpins(ct)¶

Return the spin crystal of the given type B.

This is a combinatorial model for the crystal with highest weight 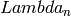$Lambda_n$ (the n-th fundamental weight). It has 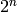$2^n$ elements, here called Spins. See also CrystalOfLetters, CrystalOfSpinsPlus and CrystalOfSpinsMinus.

INPUT:

['B',n] - A CartanType of type B.

EXAMPLES:

sage: C = CrystalOfSpins(['B',3])
sage: C.list()
[[1, 1, 1],
 [1, 1, -1],
 [1, -1, 1],
 [-1, 1, 1],
 [1, -1, -1],
 [-1, 1, -1],
 [-1, -1, 1],
 [-1, -1, -1]]
 sage: C.cartan_type()
 ['B', 3]

sage: [x.signature() for x in C]
['+++', '++-', '+-+', '-++', '+--', '-+-', '--+', '---']

TESTS:

sage: TensorProductOfCrystals(C,C,generators=[[C.list()[0],C.list()[0]]]).cardinality()
35

sage.combinat.crystals.spins.CrystalOfSpinsMinus(ct)¶

Return the minus spin crystal of the given type D.

This is the crystal with highest weight 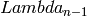$Lambda_{n-1}$ (the (n-1)-st fundamental weight).

INPUT:

['D',n] - A CartanType of type D.

EXAMPLES:

sage: E = CrystalOfSpinsMinus(['D',4])
sage: E.list()
 [[1, 1, 1, -1],
  [1, 1, -1, 1],
  [1, -1, 1, 1],
  [-1, 1, 1, 1],
  [1, -1, -1, -1],
  [-1, 1, -1, -1],
  [-1, -1, 1, -1],
  [-1, -1, -1, 1]]
sage: [x.signature() for x in E]
['+++-', '++-+', '+-++', '-+++', '+---', '-+--', '--+-', '---+']

TESTS:

sage: len(TensorProductOfCrystals(E,E,generators=[[E[0],E[0]]]).list())
35
sage: D = CrystalOfSpinsPlus(['D',4])
sage: len(TensorProductOfCrystals(D,E,generators=[[D.list()[0],E.list()[0]]]).list())
56

sage.combinat.crystals.spins.CrystalOfSpinsPlus(ct)¶

Return the plus spin crystal of the given type D.

This is the crystal with highest weight 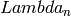$Lambda_n$ (the n-th fundamental weight).

INPUT:

['D',n] - A CartanType of type D.

EXAMPLES:

sage: D = CrystalOfSpinsPlus(['D',4])
sage: D.list()
[[1, 1, 1, 1],
 [1, 1, -1, -1],
 [1, -1, 1, -1],
 [-1, 1, 1, -1],
 [1, -1, -1, 1],
 [-1, 1, -1, 1],
 [-1, -1, 1, 1],
 [-1, -1, -1, -1]]

sage: [x.signature() for x in D]
['++++', '++--', '+-+-', '-++-', '+--+', '-+-+', '--++', '----']

TESTS:

sage: TestSuite(D).run()

class sage.combinat.crystals.spins.GenericCrystalOfSpins(ct, element_class, case)¶

Bases: sage.structure.unique_representation.UniqueRepresentation, sage.structure.parent.Parent

digraph()¶

Returns the directed graph associated to self.

EXAMPLES:

sage: CrystalOfSpins(['B',3]).digraph()
Digraph on 8 vertices

list()¶

Returns a list of the elements of self.

EXAMPLES:

sage: CrystalOfSpins(['B',3]).list()
[[1, 1, 1],
 [1, 1, -1],
 [1, -1, 1],
 [-1, 1, 1],
 [1, -1, -1],
 [-1, 1, -1],
 [-1, -1, 1],
 [-1, -1, -1]]

lt_elements(x, y)¶

Returns True if and only if there is a path from x to y in the crystal graph.

Because the crystal graph is classical, it is a directed acyclic graph which can be interpreted as a poset. This function implements the comparison function of this poset.

EXAMPLES:

sage: C = CrystalOfSpins(['B',3])
sage: x = C([1,1,1])
sage: y = C([-1,-1,-1])
sage: C.lt_elements(x,y)
True
sage: C.lt_elements(y,x)
False
sage: C.lt_elements(x,x)
False

class sage.combinat.crystals.spins.Spin(parent, value)¶

Bases: sage.combinat.crystals.letters.Letter

EXAMPLES:

sage: C = CrystalOfSpins(['B',3])
sage: c = C([1,1,1])
sage: TestSuite(c).run()

sage: C([1,1,1]).parent()
The crystal of spins for type ['B', 3]

sage: c = C([1,1,1])
sage: c._repr_()
'[1, 1, 1]'

sage: D = CrystalOfSpins(['B',4])
sage: a = C([1,1,1])
sage: b = C([-1,-1,-1])
sage: c = D([1,1,1,1])
sage: a == a
True
sage: a == b
False
sage: b == c
False

signature()¶

Returns the signature of self.

EXAMPLES:

sage: C = CrystalOfSpins(['B',3])
sage: C([1,1,1]).signature()
'+++'
sage: C([1,1,-1]).signature()
'++-'

class sage.combinat.crystals.spins.Spin_crystal_type_B_element(parent, value)¶

Bases: sage.combinat.crystals.spins.Spin

Type B spin representation crystal element

e(i)¶

Returns the action of 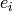$e_i$ on self.

EXAMPLES:

sage: C = CrystalOfSpins(['B',3])
sage: [[C[m].e(i) for i in range(1,4)] for m in range(8)]
[[None, None, None],
 [None, None, [1, 1, 1]],
 [None, [1, 1, -1], None],
 [[1, -1, 1], None, None],
 [None, None, [1, -1, 1]],
 [[1, -1, -1], None, [-1, 1, 1]],
 [None, [-1, 1, -1], None],
 [None, None, [-1, -1, 1]]]

f(i)¶

Returns the action of 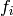$f_i$ on self.

EXAMPLES:

sage: C = CrystalOfSpins(['B',3])
sage: [[C[m].f(i) for i in range(1,4)] for m in range(8)]
[[None, None, [1, 1, -1]],
 [None, [1, -1, 1], None],
 [[-1, 1, 1], None, [1, -1, -1]],
 [None, None, [-1, 1, -1]],
 [[-1, 1, -1], None, None],
 [None, [-1, -1, 1], None],
 [None, None, [-1, -1, -1]],
 [None, None, None]]

class sage.combinat.crystals.spins.Spin_crystal_type_D_element(parent, value)¶

Bases: sage.combinat.crystals.spins.Spin

Type D spin representation crystal element

e(i)¶

Returns the action of 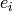$e_i$ on self.

EXAMPLES:

sage: D = CrystalOfSpinsPlus(['D',4])
sage: [[D.list()[m].e(i) for i in range(1,4)] for m in range(8)]
[[None, None, None],
 [None, None, None],
 [None, [1, 1, -1, -1], None],
 [[1, -1, 1, -1], None, None],
 [None, None, [1, -1, 1, -1]],
 [[1, -1, -1, 1], None, [-1, 1, 1, -1]],
 [None, [-1, 1, -1, 1], None],
 [None, None, None]]

sage: E = CrystalOfSpinsMinus(['D',4])
sage: [[E[m].e(i) for i in range(1,4)] for m in range(8)]
[[None, None, None],
 [None, None, [1, 1, 1, -1]],
 [None, [1, 1, -1, 1], None],
 [[1, -1, 1, 1], None, None],
 [None, None, None],
 [[1, -1, -1, -1], None, None],
 [None, [-1, 1, -1, -1], None],
 [None, None, [-1, -1, 1, -1]]]

f(i)¶

Returns the action of 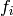$f_i$ on self.

EXAMPLES:

sage: D = CrystalOfSpinsPlus(['D',4])
sage: [[D.list()[m].f(i) for i in range(1,4)] for m in range(8)]
[[None, None, None],
 [None, [1, -1, 1, -1], None],
 [[-1, 1, 1, -1], None, [1, -1, -1, 1]],
 [None, None, [-1, 1, -1, 1]],
 [[-1, 1, -1, 1], None, None],
 [None, [-1, -1, 1, 1], None],
 [None, None, None],
 [None, None, None]]

sage: E = CrystalOfSpinsMinus(['D',4])
sage: [[E[m].f(i) for i in range(1,4)] for m in range(8)]
[[None, None, [1, 1, -1, 1]],
 [None, [1, -1, 1, 1], None],
 [[-1, 1, 1, 1], None, None],
 [None, None, None],
 [[-1, 1, -1, -1], None, None],
 [None, [-1, -1, 1, -1], None],
 [None, None, [-1, -1, -1, 1]],
 [None, None, None]]

Spin Crystals¶

Previous topic

Next topic

This Page

Navigation

Spin Crystals¶

Previous topic

Next topic

This Page

Quick search

Navigation