CLASS HIERARCHY:
SageObject
CategoryObject
Parent
TESTS: This came up in some subtle bug once.
sage: gp(2) + gap(3)
5
A simple example of registering coercions:
sage: class A_class(Parent):
... def __init__(self, name):
... Parent.__init__(self, name=name)
... self._populate_coercion_lists_()
... self.rename(name)
... #
... def category(self):
... return Sets()
... #
... def _element_constructor_(self, i):
... assert(isinstance(i, (int, Integer)))
... return ElementWrapper(i, parent = self)
...
...
sage: A = A_class("A")
sage: B = A_class("B")
sage: C = A_class("C")
sage: def f(a):
... return B(a.value+1)
...
sage: class MyMorphism(Morphism):
... def __init__(self, domain, codomain):
... Morphism.__init__(self, Hom(domain, codomain))
... #
... def _call_(self, x):
... return self.codomain()(x.value)
...
sage: f = MyMorphism(A,B)
sage: f
Generic morphism:
From: A
To: B
sage: B.register_coercion(f)
sage: C.register_coercion(MyMorphism(B,C))
sage: A(A(1)) == A(1)
True
sage: B(A(1)) == B(1)
True
sage: C(A(1)) == C(1)
True
sage: A(B(1))
...
AssertionError
Bases: sage.structure.category_object.CategoryObject
Parents are the Sage/mathematical analogues of container objects in computer science.
Return the homspace Hom(self, codomain, cat) of all homomorphisms from self to codomain in the category cat. The default category is category`().
EXAMPLES:
sage: R.<x,y> = PolynomialRing(QQ, 2)
sage: R.Hom(QQ)
Set of Homomorphisms from Multivariate Polynomial Ring in x, y over Rational Field to Rational Field
Homspaces are defined for very general Sage objects, even elements of familiar rings.
sage: n = 5; Hom(n,7)
Set of Morphisms from 5 to 7 in Category of elements of Integer Ring
sage: z=(2/3); Hom(z,8/1)
Set of Morphisms from 2/3 to 8 in Category of elements of Rational Field
This example illustrates the optional third argument:
sage: QQ.Hom(ZZ, Sets())
Set of Morphisms from Rational Field to Integer Ring in Category of sets
A parent may specify how to construct certain homsets by implementing a method _Hom_`(codomain, category). This method should either construct the requested homset or raise a ``TypeError`().
Implementation of a function that returns an element (often non-trivial) of a parent object. This is cached. Parent structures that are should override _an_element_() instead.
EXAMPLES:
sage: CDF.an_element()
1.0*I
sage: ZZ[['t']].an_element()
t
EXAMPLES:
sage: P = Parent()
sage: P.category()
Category of sets
sage: class MyParent(Parent):
... def __init__(self): pass
sage: MyParent().category()
Category of sets
Return x as an element of self, if and only if there is a canonical coercion from the parent of x to self.
EXAMPLES:
sage: QQ.coerce(ZZ(2))
2
sage: ZZ.coerce(QQ(2))
...
TypeError: no canonical coercion from Rational Field to Integer Ring
We make an exception for zero:
sage: V = GF(7)^7
sage: V.coerce(0)
(0, 0, 0, 0, 0, 0, 0)
Returns the embedding of self into some other parent, if such a parent exists.
This does not mean that there are no coercion maps from self into other fields, this is simply a specific morphism specified out of self and usually denotes a special relationship (e.g. sub-objects, choice of completion, etc.)
EXAMPLES:
This returns a Map object to coerce from S to self if one exists, or None if no such coercion exists.
EXAMPLES:
sage: ZZ.coerce_map_from(int)
Native morphism:
From: Set of Python objects of type 'int'
To: Integer Ring
sage: QQ.coerce_map_from(ZZ)
Natural morphism:
From: Integer Ring
To: Rational Field
Returns a pair (functor, parent) such that functor(parent) return self. If this ring does not have a functorial construction, return None.
EXAMPLES:
sage: QQ.construction()
(FractionField, Integer Ring)
sage: f, R = QQ['x'].construction()
sage: f
Poly[x]
sage: R
Rational Field
sage: f(R)
Univariate Polynomial Ring in x over Rational Field
This function returns a Map from S to self, which may or may not succeed on all inputs. If a coercion map from S to self exists, then the it will be returned. If a coercion from self to S exists, then it will attempt to return a section of that map.
Under the new coercion model, this is the fastest way to convert elements of S to elements of self (short of manually constructing the elements) and is used by __call__.
EXAMPLES:
sage: m = ZZ.convert_map_from(QQ)
sage: m(-35/7)
-5
sage: parent(m(-35/7))
Integer Ring
A lazy attribute for an object is like a usual attribute, except that, instead of being computed when the object is constructed (i.e. in __init__), it is computed on the fly the first time it is accessed.
For constant values attached to an object, lazy attributes provide a shorter syntax and automatic caching (unlike methods), while playing well with inheritance (like methods): a subclass can easily override a given attribute; you don’t need to call the super class constructor, etc.
Technically, a lazy_attribute is a non-data descriptor (see Invoking Descriptors in the Python reference manual).
EXAMPLES:
We create a class whose instances have a lazy attribute x:
sage: class A(object):
... def __init__(self):
... self.a=2 # just to have some data to calculate from
...
... @lazy_attribute
... def x(self):
... print "calculating x in A"
... return self.a + 1
...
For an instance a of A, a.x is calculated the first time it is accessed, and then stored as a usual attribute:
sage: a = A()
sage: a.x
calculating x in A
3
sage: a.x
3
Implementation details
We redo the same example, but opening the hood to see what happens to the internal dictionary of the object:
sage: a = A()
sage: a.__dict__
{'a': 2}
sage: a.x
calculating x in A
3
sage: a.__dict__
{'a': 2, 'x': 3}
sage: a.x
3
sage: timeit('a.x') # random
625 loops, best of 3: 89.6 ns per loop
This shows that, after the first calculation, the attribute x becomes a usual attribute; in particular, there is no time penalty to access it.
A lazy attribute may be set as usual, even before its first access, in which case the lazy calculation is completely ignored:
sage: a = A()
sage: a.x = 4
sage: a.x
4
sage: a.__dict__
{'a': 2, 'x': 4}
Class binding results in the lazy attribute itself:
sage: A.x
<sage.misc.lazy_attribute.lazy_attribute object at ...>
Conditional definitions
The function calculating the attribute may return NotImplemented to declare that, after all, it is not able to do it. In that case, the attribute lookup proceeds in the super class hierarchy:
sage: class B(A):
... @lazy_attribute
... def x(self):
... if hasattr(self, "y"):
... print "calculating x from y in B"
... return self.y
... else:
... print "y not there; B does not define x"
... return NotImplemented
...
sage: b = B()
sage: b.x
y not there; B does not define x
calculating x in A
3
sage: b = B()
sage: b.y = 1
sage: b.x
calculating x from y in B
1
Attribute existence testing
Testing for the existence of an attribute with hasattr currently always triggers its full calculation, which may not be desirable when the calculation is expensive:
sage: a = A()
sage: hasattr(a, "x")
calculating x in A
True
It would be great if we could take over the control somehow, if at all possible without a special implementation of hasattr, so as to allow for something like:
sage: class A (object):
... @lazy_attribute
... def x(self, existence_only=False):
... if existence_only:
... print "testing for x existence"
... return True
... else:
... print "calculating x in A"
... return 3
...
sage: a = A()
sage: hasattr(a, "x") # todo: not implemented
testing for x existence
sage: a.x
calculating x in A
3
sage: a.x
3
Here is a full featured example, with both conditional definition and existence testing:
sage: class B(A):
... @lazy_attribute
... def x(self, existence_only=False):
... if hasattr(self, "y"):
... if existence_only:
... print "testing for x existence in B"
... return True
... else:
... print "calculating x from y in B"
... return self.y
... else:
... print "y not there; B does not define x"
... return NotImplemented
...
sage: b = B()
sage: hasattr(b, "x") # todo: not implemented
y not there; B does not define x
testing for x existence
True
sage: b.x
y not there; B does not define x
calculating x in A
3
sage: b = B()
sage: b.y = 1
sage: hasattr(b, "x") # todo: not implemented
testing for x existence in B
True
sage: b.x
calculating x from y in B
1
lazy attributes and introspection
TODO: make the following work nicely:
sage: b.x? # todo: not implemented
sage: b.x?? # todo: not implemented
Right now, the first one includes the doc of this class, and the second one brings up the code of this class, both being not very useful.
TESTS:
.. rubric:: Partial support for old style classes
Old style and new style classes play a bit differently with @property and attribute setting:
sage: class A:
... @property
... def x(self):
... print "calculating x"
... return 3
...
sage: a = A()
sage: a.x = 4
sage: a.__dict__
{'x': 4}
sage: a.x
4
sage: a.__dict__['x']=5
sage: a.x
5
sage: class A (object):
... @property
... def x(self):
... print "calculating x"
... return 3
...
sage: a = A()
sage: a.x = 4
...
AttributeError: can't set attribute
sage: a.__dict__
{}
sage: a.x
calculating x
3
sage: a.__dict__['x']=5
sage: a.x
calculating x
3
In particular, lazy_attributes need to be implemented as non-data descriptors for new style classes, so as to leave access to setattr. We now check that this implementation also works for old style classes (conditional definition does not work yet):
sage: class A:
... def __init__(self):
... self.a=2 # just to have some data to calculate from
...
... @lazy_attribute
... def x(self):
... print "calculating x"
... return self.a + 1
...
sage: a = A()
sage: a.__dict__
{'a': 2}
sage: a.x
calculating x
3
sage: a.__dict__
{'a': 2, 'x': 3}
sage: a.x
3
sage: timeit('a.x') # random
625 loops, best of 3: 115 ns per loop
sage: a = A()
sage: a.x = 4
sage: a.x
4
sage: a.__dict__
{'a': 2, 'x': 4}
sage: class B(A):
... @lazy_attribute
... def x(self):
... if hasattr(self, "y"):
... print "calculating x from y in B"
... return self.y
... else:
... print "y not there; B does not define x"
... return NotImplemented
...
sage: b = B()
sage: b.x # todo: not implemented
y not there; B does not define x
calculating x in A
3
sage: b = B()
sage: b.y = 1
sage: b.x
calculating x from y in B
1
lazy_attributes and cpdef functions
This attempts to check that lazy_attributes work with built-in functions like cpdef methods:
sage: class A:
... def __len__(x):
... return int(5)
... len = lazy_attribute(len)
...
sage: A().len
5
About descriptor specifications
The specifications of descriptors (see 3.4.2.3 Invoking Descriptors in the Python reference manual) are incomplete w.r.t. inheritance, and maybe even ill-implemented. We illustrate this on a simple class hierarchy, with an instrumented descriptor:
sage: class descriptor(object):
... def __get__(self, obj, cls):
... print cls
... return 1
...
sage: class A(object):
... x = descriptor()
...
sage: class B(A):
... pass
...
This is fine:
sage: A.x
<class '__main__.A'>
1
The behaviour for the following case is not specified (see Instance Binding) when x is not in the dictionary of B but in that of some super category:
sage: B().x
<class '__main__.B'>
1
It would seem more natural (and practical!) to get A rather than B.
From the specifications for Super Binding, it would be expected to get A and not B as cls parameter:
sage: super(B, B()).x
<class '__main__.B'>
1
Due to this, the natural implementation runs into an infinite loop in the following example:
sage: class A(object):
... @lazy_attribute
... def unimplemented_A(self):
... return NotImplemented
... @lazy_attribute
... def unimplemented_AB(self):
... return NotImplemented
... @lazy_attribute
... def unimplemented_B_implemented_A(self):
... return 1
...
sage: class B(A):
... @lazy_attribute
... def unimplemented_B(self):
... return NotImplemented
... @lazy_attribute
... def unimplemented_AB(self):
... return NotImplemented
... @lazy_attribute
... def unimplemented_B_implemented_A(self):
... return NotImplemented
...
sage: class C(B):
... pass
...
This is the simplest case where, without workaround, we get an infinite loop:
sage: hasattr(B(), "unimplemented_A") # todo: not implemented
False
TODO: improve the error message:
sage: B().unimplemented_A # todo: not implemented
...
AttributeError: 'super' object has no attribute 'unimplemented_A'
We now make some systematic checks:
sage: B().unimplemented_A
...
AttributeError: '...' object has no attribute 'unimplemented_A'
sage: B().unimplemented_B
...
AttributeError: '...' object has no attribute 'unimplemented_B'
sage: B().unimplemented_AB
...
AttributeError: '...' object has no attribute 'unimplemented_AB'
sage: B().unimplemented_B_implemented_A
1
sage: C().unimplemented_A()
...
AttributeError: '...' object has no attribute 'unimplemented_A'
sage: C().unimplemented_B()
...
AttributeError: '...' object has no attribute 'unimplemented_B'
sage: C().unimplemented_AB()
...
AttributeError: '...' object has no attribute 'unimplemented_AB'
sage: C().unimplemented_B_implemented_A # todo: not implemented
1
Returns an action of self on S or S on self.
To provide additional actions, override _get_action_().
TESTS:
sage: M = QQ['y']^3
sage: M.get_action(ZZ['x']['y'])
Right scalar multiplication by Univariate Polynomial Ring in y over Univariate Polynomial Ring in x over Integer Ring on Ambient free module of rank 3 over the principal ideal domain Univariate Polynomial Ring in y over Rational Field
sage: M.get_action(ZZ['x']) # should be None
Return True if there is a natural map from S to self. Otherwise, return False.
EXAMPLES:
sage: RDF.has_coerce_map_from(QQ)
True
sage: RDF.has_coerce_map_from(QQ['x'])
False
sage: RDF['x'].has_coerce_map_from(QQ['x'])
True
sage: RDF['x,y'].has_coerce_map_from(QQ['x'])
True
Return the unique homomorphism from self to codomain that sends self.gens() to the entries of im_gens. Raises a TypeError if there is no such homomorphism.
INPUT:
OUTPUT:
Note
As a shortcut, one can also give an object X instead of im_gens, in which case return the (if it exists) natural map to X.
EXAMPLE: Polynomial Ring We first illustrate construction of a few homomorphisms involving a polynomial ring.
sage: R.<x> = PolynomialRing(ZZ)
sage: f = R.hom([5], QQ)
sage: f(x^2 - 19)
6
sage: R.<x> = PolynomialRing(QQ)
sage: f = R.hom([5], GF(7))
...
TypeError: images do not define a valid homomorphism
sage: R.<x> = PolynomialRing(GF(7))
sage: f = R.hom([3], GF(49,'a'))
sage: f
Ring morphism:
From: Univariate Polynomial Ring in x over Finite Field of size 7
To: Finite Field in a of size 7^2
Defn: x |--> 3
sage: f(x+6)
2
sage: f(x^2+1)
3
EXAMPLE: Natural morphism
sage: f = ZZ.hom(GF(5))
sage: f(7)
2
sage: f
Ring Coercion morphism:
From: Integer Ring
To: Finite Field of size 5
There might not be a natural morphism, in which case a TypeError exception is raised.
sage: QQ.hom(ZZ)
...
TypeError: Natural coercion morphism from Rational Field to Integer Ring not defined.
Return True if elements of this ring are represented exactly, i.e., there is no precision loss when doing arithmetic.
NOTE: This defaults to true, so even if it does return True you have no guarantee (unless the ring has properly overloaded this).
Update the coercion model to use action to act on self.
action should be of type sage.categories.action.Action.
EXAMPLES:
sage: import sage.categories.action
sage: import operator
sage: class SymmetricGroupAction(sage.categories.action.Action):
... "Act on a multivariate polynomial ring by permuting the generators."
... def __init__(self, G, M, is_left=True):
... sage.categories.action.Action.__init__(self, G, M, is_left, operator.mul)
...
... def _call_(self, g, a):
... if not self.is_left():
... g, a = a, g
... D = {}
... for k, v in a.dict().items():
... nk = [0]*len(k)
... for i in range(len(k)):
... nk[g(i+1)-1] = k[i]
... D[tuple(nk)] = v
... return a.parent()(D)
sage: R.<x, y, z> = QQ['x, y, z']
sage: G = SymmetricGroup(3)
sage: act = SymmetricGroupAction(G, R)
sage: t = x + 2*y + 3*z
sage: act(G((1, 2)), t)
2*x + y + 3*z
sage: act(G((2, 3)), t)
x + 3*y + 2*z
sage: act(G((1, 2, 3)), t)
3*x + y + 2*z
This should fail, since we haven’t registered the left action:
sage: G((1,2)) * t
...
TypeError: ...
Now let’s make it work:
sage: R._unset_coercions_used()
sage: R.register_action(act)
sage: G((1, 2)) * t
2*x + y + 3*z
Update the coercion model to use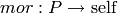 
to coerce
from a parent P into self.
For safety, an error is raised if another coercion has already been registered or discovered between P and self.
EXAMPLES:
sage: K.<a> = ZZ['a']
sage: L.<b> = ZZ['b']
sage: L_into_K = L.hom([-a]) # non-trivial automorphism
sage: K.register_coercion(L_into_K)
sage: K(0) + b
-a
sage: a + b
0
sage: K(b) # check that convert calls coerce first; normally this is just a
-a
sage: L(0) + a in K # this goes through the coercion mechanism of K
True
sage: L(a) in L # this still goes through the convert mechanism of L
True
sage: K.register_coercion(L_into_K)
...
AssertionError: coercion from Univariate Polynomial Ring in b over Integer Ring to Univariate Polynomial Ring in a over Integer Ring already registered or discovered
Update the coercion model to use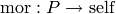 
to convert
from P into self.
EXAMPLES:
sage: K.<a> = ZZ['a']
sage: M.<c> = ZZ['c']
sage: M_into_K = M.hom([a]) # trivial automorphism
sage: K._unset_coercions_used()
sage: K.register_conversion(M_into_K)
sage: K(c)
a
sage: K(0) + c
...
TypeError: ...
Update the coercion model to use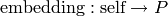 
to embed self into the parent P.
There can only be one embedding registered; it can only be registered once; and it must be registered before using this parent in the coercion model.
EXAMPLES:
sage: S3 = AlternatingGroup(3)
sage: G = SL(3, QQ)
sage: p = S3[2]; p.matrix()
[0 0 1]
[1 0 0]
[0 1 0]
By default, one can’t mix matrices and permutations:
sage: G(p)
...
TypeError: Cannot coerce (1,3,2) to a 3-by-3 matrix over Rational Field
sage: G(1) * p
...
TypeError: ...
sage: phi = S3.hom(lambda p: G(p.matrix()), codomain = G)
sage: phi(p)
[0 0 1]
[1 0 0]
[0 1 0]
sage: S3._unset_coercions_used()
sage: S3.register_embedding(phi)
sage: S3.coerce_embedding()
Generic morphism:
From: AlternatingGroup(3)
To: Special Linear Group of degree 3 over Rational Field
sage: S3.coerce_embedding()(p)
[0 0 1]
[1 0 0]
[0 1 0]
Hmm, some more work is apparently in order:
sage: G(p) # todo: not implemented
sage: G(1) * p # todo: not implemented
The following more advanced examples fail since Sage 4.3, by lack of support for field morphisms from a field into a subfield of an algebra (they worked by abuse beforehand).
sage: x = QQ[‘x’].0 sage: t = abs(ZZ.random_element(10^6)) sage: K = NumberField(x^2 + 2*3*7*11, “a”+str(t)) sage: a = K.gen() sage: K_into_MS = K.hom([a.matrix()]) # todo: not implemented sage: K._unset_coercions_used() sage: K.register_embedding(K_into_MS) # todo: not implemented
sage: L = NumberField(x^2 + 2*3*7*11*19*31, “b”+str(abs(ZZ.random_element(10^6)))) sage: b = L.gen() sage: L_into_MS = L.hom([b.matrix()]) # todo: not implemented sage: L._unset_coercions_used() sage: L.register_embedding(L_into_MS) # todo: not implemented
sage: K.coerce_embedding()(a) # todo: not implemented [ 0 1] [-462 0] sage: L.coerce_embedding()(b) # todo: not implemented [ 0 1] [-272118 0]
sage: a.matrix() * b # todo: not implemented [-272118 0] [ 0 -462] sage: a * b.matrix() # todo: not implemented [-272118 0] [ 0 -462]
Return the (unique) Parent that represents the set of Python objects of a specified type.
EXAMPLES:
sage: from sage.structure.parent import Set_PythonType
sage: Set_PythonType(list)
Set of Python objects of type 'list'
sage: Set_PythonType(list) is Set_PythonType(list)
True
sage: S = Set_PythonType(tuple)
sage: S([1,2,3])
(1, 2, 3)
S is a parent which models the set of all lists:
sage: S.category()
Category of sets
Bases: sage.structure.parent.Set_generic
EXAMPLES:
sage: S = sage.structure.parent.Set_PythonType(bool)
sage: S.cardinality()
2
sage: S = sage.structure.parent.Set_PythonType(int)
sage: S.cardinality()
4294967296 # 32-bit
18446744073709551616 # 64-bit
sage: S = sage.structure.parent.Set_PythonType(float)
sage: S.cardinality()
18437736874454810627
sage: S = sage.structure.parent.Set_PythonType(long)
sage: S.cardinality()
+Infinity
EXAMPLES:
sage: S = sage.structure.parent.Set_PythonType(tuple)
sage: S.object()
<type 'tuple'>
Bases: sage.structure.parent.Parent
Abstract base class for sets.
TESTS:
sage: Set(QQ).category()
Category of sets
Emulates dir(self), as if self was also an instance cls, right after caller_class in the method resolution order (self.__class__.mro())
EXAMPLES:
sage: class A(object):
... a = 1
... b = 2
... c = 3
sage: class B(object):
... b = 2
... c = 3
... d = 4
sage: x = A()
sage: x.c = 1; x.e = 1
sage: sage.structure.parent.dir_with_other_class(x, B)
[..., 'a', 'b', 'c', 'd', 'e']
Check that objects without dicts are well handled
sage: F.<x0,x1> = BooleanPolynomialRing() sage: hasattr(F, ‘__dict__’) False sage: sage.structure.parent.dir_with_other_class(F, B) [..., ... ‘__class__’, ..., ‘_test_pickling’, ..., ‘b’, ..., ‘extension’, ...]
INPUT:
- ``self``: some object
- ``cls``: a class
- ``name``: a string
Emulates getattr(self, name), as if self was an instance of cls.
If self is an instance of cls, raises an AttributeError, to avoid a double lookup. This function is intended to be called from __getattr__, and so should not be called if name is an attribute of self.
TODO: lookup if such a function readilly exists in Python, and if not triple check this specs and make this implementation rock-solid.
Caveat: this is pretty hacky, does not handle caching, there is no guarantee of robustness with super calls and descriptors, ...
EXAMPLES:
sage: from sage.structure.parent import getattr_from_other_class
sage: class A(object):
... def inc(self):
... return self + 1
... @lazy_attribute
... def lazy_attribute(self):
... return repr(self)
sage: getattr_from_other_class(1, A, "inc")
<bound method A.inc of 1>
sage: getattr_from_other_class(1, A, "inc")()
2
Caveat: lazy attributes don’t work currently with extension types, with or without a __dict__:
sage: getattr_from_other_class(1, A, “lazy_attribute”) Traceback (most recent call last): ... AttributeError: ‘sage.rings.integer.Integer’ object has no attribute ‘lazy_attribute’ sage: getattr_from_other_class(ZZ, A, “lazy_attribute”) Traceback (most recent call last): ... AttributeError: ‘sage.rings.integer_ring.IntegerRing_class’ object has no attribute ‘lazy_attribute’ sage: getattr_from_other_class(QQ[x].one(), A, “lazy_attribute”) ‘1’
In general, descriptors are not yet well supported, because they often do not accept to be cheated with the type of their instance:
sage: A.__weakref__.__get__(1)
...
TypeError: descriptor '__weakref__' for 'A' objects doesn't apply to 'sage.rings.integer.Integer' object
When this occurs, an AttributeError is raised:
sage: getattr_from_other_class(1, A, "__weakref__")
...
AttributeError: 'sage.rings.integer.Integer' object has no attribute '__weakref__'
This was caught by #8296 for which we do a couple more tests:
sage: "__weakref__" in dir(A)
True
sage: "__weakref__" in dir(1)
True
sage: 1.__weakref__
...
AttributeError: 'sage.rings.integer.Integer' object has no attribute '__weakref__'
sage: import IPython
sage: _ip = IPython.ipapi.get()
sage: _ip.IP.magic_psearch('n.__weakref__') # not tested: only works with an interactive shell running
Caveat: When __call__ is not defined for instances, using A.__call__ yields the method __call__ of the class. We use a workaround but there is no guarantee for robustness.
sage: getattr_from_other_class(1, A, “__call__”) Traceback (most recent call last): ... AttributeError: ‘sage.rings.integer.Integer’ object has no attribute ‘__call__’
Return True if x is a parent object, i.e., derives from sage.structure.parent.Parent and False otherwise.
EXAMPLES:
sage: from sage.structure.parent import is_Parent
sage: is_Parent(2/3)
False
sage: is_Parent(ZZ)
True
sage: is_Parent(Primes())
True
Tests whether cls is an extension type (int, list, cython compiled classes, ...)
TESTS:
sage: sage.structure.parent.normalize_names(5, 'x')
('x0', 'x1', 'x2', 'x3', 'x4')
sage: sage.structure.parent.normalize_names(2, ['x','y'])
('x', 'y')
Tries to emulate the standard Python AttributeError exception
EXAMPLES:
sage: sage.structure.parent.raise_attribute_error(1, "bla")
...
AttributeError: 'sage.rings.integer.Integer' object has no attribute 'bla'
sage: sage.structure.parent.raise_attribute_error(QQ[x].gen(), "bla")
...
AttributeError: 'Polynomial_rational_dense' object has no attribute 'bla'