Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Combinatorics »
- Crystals »

Bases: sage.combinat.crystals.kirillov_reshetikhin.KirillovReshetikhinCrystalFromPromotion
Class of Kirillov-Reshetikhin crystals of type 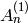 .
.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['A',3,1], 2,2)
sage: b = K(rows=[[1,2],[2,4]])
sage: b.f(0)
[[1, 1], [2, 2]]
Specifies the classical crystal underlying the KR crystal of type A.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['A',3,1], 2,2)
sage: K.classical_decomposition()
The crystal of tableaux of type ['A', 3] and shape(s) [[2, 2]]
Specifies the Dynkin diagram automorphism underlying the promotion action on the crystal elements. The automorphism needs to map node 0 to some other Dynkin node.
For type A we use the Dynkin diagram automorphism which maps i to i+1 mod n+1, where n is the rank.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['A',3,1], 2,2)
sage: K.dynkin_diagram_automorphism(0)
1
sage: K.dynkin_diagram_automorphism(3)
0
Specifies the promotion operator used to construct the affine type A crystal. For type A this corresponds to the Dynkin diagram automorphism which maps i to i+1 mod n+1, where n is the rank.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal([‘A’,3,1], 2,2) sage: b = K.classical_decomposition()(rows=[[1,2],[3,4]]) sage: K.promotion()(b) [[1, 3], [2, 4]]
Specifies the inverse promotion operator used to construct the affine type A crystal. For type A this corresponds to the Dynkin diagram automorphism which maps i to i-1 mod n+1, where n is the rank.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal([‘A’,3,1], 2,2) sage: b = K.classical_decomposition()(rows=[[1,3],[2,4]]) sage: K.promotion_inverse()(b) [[1, 2], [3, 4]] sage: b = K.classical_decomposition()(rows=[[1,2],[3,3]]) sage: K.promotion_inverse()(K.promotion()(b)) [[1, 2], [3, 3]]
Bases: sage.combinat.crystals.kirillov_reshetikhin.KirillovReshetikhinGenericCrystal, sage.combinat.crystals.affine.AffineCrystalFromClassical
Class of Kirillov-Reshetikhin crystals 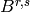 of type
of type 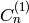 for
for 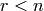 .
.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['C',2,1], 1,2)
sage: K
Kirillov-Reshetikhin crystal of type ['C', 2, 1] with (r,s)=(1,2)
sage: b = K(rows=[])
sage: b.f(0)
[[1, 1]]
sage: b.e(0)
[[-1, -1]]
Returns the ambient crystal 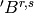 of type
of type 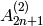 associated to the Kirillov-Reshetikhin
crystal of type
associated to the Kirillov-Reshetikhin
crystal of type 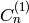 . This ambient crystal is used to construct the zero arrows.
. This ambient crystal is used to construct the zero arrows.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['C',3,1], 2,3)
sage: K.ambient_crystal()
Kirillov-Reshetikhin crystal of type ['B', 4, 1]^* with (r,s)=(2,3)
Gives a dictionary of all self-dual  diagrams for the ambient crystal.
Their key is their inner shape.
diagrams for the ambient crystal.
Their key is their inner shape.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['C',2,1], 1,2)
sage: K.ambient_dict_pm_diagrams()
{[]: [[1, 1], [0]], [2]: [[0, 0], [2]]}
sage: K = KirillovReshetikhinCrystal(['C',3,1], 2,2)
sage: K.ambient_dict_pm_diagrams()
{[2, 2]: [[0, 0], [0, 0], [2]], []: [[1, 1], [0, 0], [0]], [2]: [[0, 0], [1, 1], [0]]}
sage: K = KirillovReshetikhinCrystal(['C',3,1], 2,3)
sage: K.ambient_dict_pm_diagrams()
{[3, 3]: [[0, 0], [0, 0], [3]], [3, 1]: [[0, 0], [1, 1], [1]], [1, 1]: [[1, 1], [0, 0], [1]]}
Gives a dictionary of all 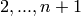 -highest weight vectors in the ambient crystal.
Their key is the inner shape of their corresponding
-highest weight vectors in the ambient crystal.
Their key is the inner shape of their corresponding 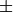 diagram, or equivalently, their
diagram, or equivalently, their
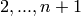 weight.
weight.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['C',3,1], 2,2)
sage: K.ambient_highest_weight_dict()
{[]: [[2], [-2]], [2, 2]: [[2, 2], [3, 3]], [2]: [[1, 2], [2, -1]]}
Specifies the classical crystal underlying the Kirillov-Reshetikhin crystal of type 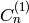 .
It is given by
.
It is given by 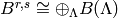 where
where 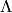 are weights obtained from
a rectangle of width s and height r by removing horizontal dominoes. Here we identify the fundamental
weight
are weights obtained from
a rectangle of width s and height r by removing horizontal dominoes. Here we identify the fundamental
weight 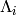 with a column of height
with a column of height  .
.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['C',3,1], 2,2)
sage: K.classical_decomposition()
The crystal of tableaux of type ['C', 3] and shape(s) [[], [2], [2, 2]]
Provides a map from the ambient crystal of type 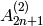 to the Kirillov-Reshetikhin crystal of
type
to the Kirillov-Reshetikhin crystal of
type 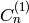 . Note that this map is only well-defined on elements that are in the image
type
. Note that this map is only well-defined on elements that are in the image
type 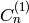 elements under
elements under 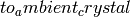 .
.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['C',3,1], 2,2)
sage: b=K.ambient_crystal()(rows=[[2,2],[3,3]])
sage: K.from_ambient_crystal()(b)
[[1, 1], [2, 2]]
Gives a dictionary of the classical highest weight vectors of self. Their key is their shape.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['C',3,1], 2,2)
sage: K.highest_weight_dict()
{[2, 2]: [[1, 1], [2, 2]], []: [], [2]: [[1, 1]]}
Provides a map from the Kirillov-Reshetikhin crystal of type 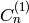 to the
ambient crystal of type
to the
ambient crystal of type 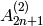 .
.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['C',3,1], 2,2)
sage: b=K(rows=[[1,1]])
sage: K.to_ambient_crystal()(b)
[[1, 2], [2, -1]]
sage: b=K(rows=[])
sage: K.to_ambient_crystal()(b)
[[2], [-2]]
sage: K.to_ambient_crystal()(b).parent() # Anne: please check this!!!!
Kirillov-Reshetikhin crystal of type ['B', 4, 1]^* with (r,s)=(2,2)
Bases: sage.combinat.crystals.affine.AffineCrystalFromClassicalElement
Class for the elements in the Kirillov-Reshetikhin crystals 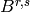 of type
of type 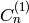 for
for 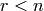 .
.
EXAMPLES:
sage: K=KirillovReshetikhinCrystal(['C',3,1],1,2)
sage: type(K.module_generators[0])
<class 'sage.combinat.crystals.kirillov_reshetikhin.KR_type_C_with_category.element_class'>
Gives 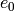 on self by mapping self to the ambient crystal, calculating
on self by mapping self to the ambient crystal, calculating 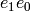 there and
pulling the element back.
there and
pulling the element back.
EXAMPLES:
sage: K=KirillovReshetikhinCrystal(['C',3,1],1,2)
sage: b = K(rows=[])
sage: b.e(0)
[[-1, -1]]
Calculates 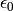 of self by mapping the element to the ambient crystal
and calculating
of self by mapping the element to the ambient crystal
and calculating 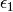 there.
there.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['C',2,1], 1,2)
sage: b=K(rows=[[1,1]])
sage: b.epsilon(0)
2
Gives 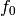 on self by mapping self to the ambient crystal, calculating
on self by mapping self to the ambient crystal, calculating 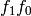 there and
pulling the element back.
there and
pulling the element back.
EXAMPLES:
sage: K=KirillovReshetikhinCrystal(['C',3,1],1,2)
sage: b = K(rows=[])
sage: b.f(0)
[[1, 1]]
Calculates 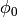 of self by mapping the element to the ambient crystal
and calculating
of self by mapping the element to the ambient crystal
and calculating 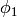 there.
there.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['C',2,1], 1,2)
sage: b=K(rows=[[-1,-1]])
sage: b.phi(0)
2
Bases: sage.combinat.crystals.kirillov_reshetikhin.KirillovReshetikhinCrystalFromPromotion
Class of Kirillov-Reshetikhin crystals of type 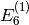 for
for 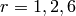 .
.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['E',6,1],2,1)
sage: K.module_generator().e(0)
[]
sage: K.module_generator().e(0).f(0)
[[[2, -1], [1]]]
sage: K = KirillovReshetikhinCrystal(['E',6,1], 1,1)
sage: b = K.module_generator()
sage: b
[[1]]
sage: b.e(0)
[[-2, 1]]
sage: b = [t for t in K if t.epsilon(1) == 1 and t.phi(3) == 1 and t.phi(2) == 0 and t.epsilon(2) == 0][0]
sage: b
[[-1, 3]]
sage: b.e(0)
[[-1, -2, 3]]
The elements of the Kirillov-Reshetikhin crystals can be constructed from a classical crystal element using rectract().
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['E',6,1],2,1)
sage: La = K.cartan_type().classical().root_system().weight_lattice().fundamental_weights()
sage: H = HighestWeightCrystal(La[2])
sage: t = H.module_generator()
sage: t
[[[2, -1], [1]]]
sage: type(K.retract(t))
<class 'sage.combinat.crystals.affine.KR_type_E6_with_category.element_class'>
sage: K.retract(t).e(0)
[]
TESTS:
sage: K = KirillovReshetikhinCrystal(['E',6,1], 2,1)
sage: La = K.weight_lattice_realization().fundamental_weights()
sage: all(b.weight() == sum( (K.affine_weight(b.lift())[i] * La[i] for i in K.index_set()), 0*La[0]) for b in K)
True
Returns the affine level zero weight corresponding to the element b of the classical crystal underlying self. For the coefficients to calculate the level, see Kac pg. 48.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['E',6,1],2,1)
sage: [K.affine_weight(x.lift()) for x in K if all(x.epsilon(i) == 0 for i in [2,3,4,5])]
[(0, 0, 0, 0, 0, 0, 0),
(-2, 0, 1, 0, 0, 0, 0),
(-1, -1, 0, 0, 0, 1, 0),
(0, 0, 0, 0, 0, 0, 0),
(0, 0, 0, 0, 0, 1, -2),
(0, -1, 1, 0, 0, 0, -1),
(-1, 0, 0, 1, 0, 0, -1),
(-1, -1, 0, 0, 1, 0, -1),
(0, 0, 0, 0, 0, 0, 0),
(0, -2, 0, 1, 0, 0, 0)]
Acts with the Dynkin diagram automorphism on affine weights as outputted by the affine_weight method.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['E',6,1],2,1)
sage: [[x[0], K.automorphism_on_affine_weight(x[0])] for x in K.highest_weight_dict().values()]
[[(-1, 0, 0, 1, 0, 0, -1), (-1, -1, 0, 0, 0, 1, 0)],
[(0, 0, 0, 0, 0, 1, -2), (-2, 0, 1, 0, 0, 0, 0)],
[(-2, 0, 1, 0, 0, 0, 0), (0, -2, 0, 1, 0, 0, 0)],
[(0, 0, 0, 0, 0, 0, 0), (0, 0, 0, 0, 0, 0, 0)],
[(0, 0, 0, 0, 0, 0, 0), (0, 0, 0, 0, 0, 0, 0)]]
Specifies the classical crystal underlying the KR crystal of type 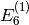 .
.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['E',6,1], 2,2)
sage: K.classical_decomposition()
Direct sum of the crystals Family (Finite dimensional highest weight crystal of type ['E', 6] and highest weight 0, Finite dimensional highest weight crystal of type ['E', 6] and highest weight Lambda[2], Finite dimensional highest weight crystal of type ['E', 6] and highest weight 2*Lambda[2])
sage: K = KirillovReshetikhinCrystal(['E',6,1], 1,2)
sage: K.classical_decomposition()
Direct sum of the crystals Family (Finite dimensional highest weight crystal of type ['E', 6] and highest weight 2*Lambda[1],)
Specifies the Dynkin diagram automorphism underlying the promotion action on the crystal elements. The automorphism needs to map node 0 to some other Dynkin node.
Here we use the Dynkin diagram automorphism of order 3 which maps node 0 to node 1.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['E',6,1],2,1)
sage: [K.dynkin_diagram_automorphism(i) for i in K.index_set()]
[1, 6, 3, 5, 4, 2, 0]
Returns a dictionary between 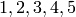 highest weight elements, and a tuple of affine weights and its classical component.
highest weight elements, and a tuple of affine weights and its classical component.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['E',6,1],2,1)
sage: K.highest_weight_dict()
{[[[3, -1, -6], [1]]]: ((-1, 0, 0, 1, 0, 0, -1), 1),
[[[5, -2, -6], [-6, 2]]]: ((0, 0, 0, 0, 0, 1, -2), 1),
[[[2, -1], [1]]]: ((-2, 0, 1, 0, 0, 0, 0), 1),
[[[6, -2], [-6, 2]]]: ((0, 0, 0, 0, 0, 0, 0), 1),
[]: ((0, 0, 0, 0, 0, 0, 0), 0)}
Returns a dictionary between a tuple of affine weights and a classical component, and
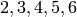 highest weight elements.
highest weight elements.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['E',6,1],2,1)
sage: K.highest_weight_dict_inv()
{((0, 0, 0, 0, 0, 0, 0), 0): [],
((-1, -1, 0, 0, 0, 1, 0), 1): [[[5, -3], [-1, 3]]],
((0, 0, 0, 0, 0, 0, 0), 1): [[[1, -3], [-1, 3]]],
((0, -2, 0, 1, 0, 0, 0), 1): [[[-1], [-1, 3]]],
((-2, 0, 1, 0, 0, 0, 0), 1): [[[2, -1], [1]]]}
Returns the 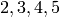 highest weight elements of self.
highest weight elements of self.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['E',6,1],2,1)
sage: K.hw_auxiliary()
[[], [[[2, -1], [1]]], [[[5, -3], [-1, 3]]], [[[6, -2], [-6, 2]]],
[[[5, -2, -6], [-6, 2]]], [[[-1], [-6, 2]]], [[[3, -1, -6], [1]]],
[[[4, -3, -6], [-1, 3]]], [[[1, -3], [-1, 3]]], [[[-1], [-1, 3]]]]
Specifies the promotion operator used to construct the affine type 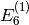 crystal.
crystal.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal([‘E’,6,1], 2,1) sage: promotion = K.promotion() sage: all(promotion(promotion(promotion(b))) == b for b in K.classical_decomposition()) True sage: K = KirillovReshetikhinCrystal([‘E’,6,1],1,1) sage: promotion = K.promotion() sage: all(promotion(promotion(promotion(b))) == b for b in K.classical_decomposition()) True
Returns the inverse promotion. Since promotion is of order 3, the inverse promotion is the same as promotion applied twice.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['E',6,1], 2,1)
sage: p = K.promotion()
sage: p_inv = K.promotion_inverse()
sage: all(p_inv(p(b)) == b for b in K.classical_decomposition())
True
Gives a dictionary of the promotion map on 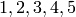 highest weight elements to
highest weight elements to
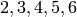 elements in self.
elements in self.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['E',6,1],2,1)
sage: dic = K.promotion_on_highest_weight_vectors()
sage: dic
{[[[2, -1], [1]]]: [[[-1], [-1, 3]]],
[[[5, -2, -6], [-6, 2]]]: [[[2, -1], [1]]],
[[[3, -1, -6], [1]]]: [[[5, -3], [-1, 3]]],
[[[6, -2], [-6, 2]]]: [], []: [[[1, -3], [-1, 3]]]}
Bases: sage.combinat.crystals.kirillov_reshetikhin.KirillovReshetikhinGenericCrystal, sage.combinat.crystals.affine.AffineCrystalFromClassical
Class of Kirillov-Reshetikhin crystals 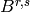 of type
of type 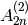 for
for 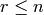 and type
and type 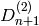 for
for 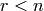 .
.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['A',4,2], 1,1)
sage: K
Kirillov-Reshetikhin crystal of type ['BC', 2, 2] with (r,s)=(1,1)
sage: b = K(rows=[])
sage: b.f(0)
[[1]]
sage: b.e(0)
[[-1]]
Returns the ambient crystal 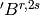 of type
of type 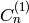 associated to the Kirillov-Reshetikhin.
This ambient crystal is used to construct the zero arrows.
associated to the Kirillov-Reshetikhin.
This ambient crystal is used to construct the zero arrows.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['A',4,2], 2,2)
sage: K.ambient_crystal()
Kirillov-Reshetikhin crystal of type ['C', 2, 1] with (r,s)=(2,4)
Gives a dictionary of the classical highest weight vectors of the ambient crystal of self. Their key is their shape.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['A',6,2], 2,2)
sage: K.ambient_highest_weight_dict()
{[4, 2]: [[1, 1, 1, 1], [2, 2]], [2, 2]: [[1, 1], [2, 2]], []: [], [4]: [[1, 1, 1, 1]], [4, 4]: [[1, 1, 1, 1], [2, 2, 2, 2]],
[2]: [[1, 1]]}
Specifies the classical crystal underlying the Kirillov-Reshetikhin crystal of type 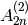 and
and 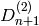 .
It is given by
.
It is given by 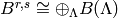 where
where 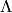 are weights obtained from
a rectangle of width s and height r by removing boxes. Here we identify the fundamental
weight
are weights obtained from
a rectangle of width s and height r by removing boxes. Here we identify the fundamental
weight 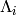 with a column of height
with a column of height  .
.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['A',4,2], 2,2)
sage: K.classical_decomposition()
The crystal of tableaux of type ['C', 2] and shape(s) [[], [1], [2], [1, 1], [2, 1], [2, 2]]
sage: K = KirillovReshetikhinCrystal(['D',4,2], 2,3)
sage: K.classical_decomposition()
The crystal of tableaux of type ['B', 3] and shape(s) [[], [1], [2], [1, 1], [3], [2, 1], [3, 1], [2, 2], [3, 2], [3, 3]]
Provides a map from the ambient crystal of type 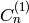 to the Kirillov-Reshetikhin crystal self.
Note that this map is only well-defined on elements that are in the image under
to the Kirillov-Reshetikhin crystal self.
Note that this map is only well-defined on elements that are in the image under 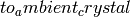 .
.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['D',4,2], 1,1)
sage: b = K.ambient_crystal()(rows=[[3,-3]])
sage: K.from_ambient_crystal()(b)
[[0]]
sage: K = KirillovReshetikhinCrystal(['A',4,2], 1,1)
sage: b = K.ambient_crystal()(rows=[])
sage: K.from_ambient_crystal()(b)
[]
Gives a dictionary of the classical highest weight vectors of self. Their key is 2 times their shape.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['A',6,2], 2,2)
sage: K.highest_weight_dict()
{[4, 2]: [[1, 1], [2]], [2, 2]: [[1], [2]], []: [], [4]: [[1, 1]], [4, 4]: [[1, 1], [2, 2]], [2]: [[1]]}
Sets the similarity factor used to map to the ambient crystal.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['A',6,2], 2,2)
sage: K.similarity_factor()
{1: 2, 2: 2, 3: 2}
sage: K = KirillovReshetikhinCrystal(['D',5,2], 1,1)
sage: K.similarity_factor()
{1: 2, 2: 2, 3: 2, 4: 1}
Provides a map from self to the ambient crystal of type 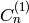 .
.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['D',4,2], 1,1)
sage: [K.to_ambient_crystal()(b) for b in K]
[[], [[1, 1]], [[2, 2]], [[3, 3]], [[3, -3]], [[-3, -3]], [[-2, -2]], [[-1, -1]]]
sage: K = KirillovReshetikhinCrystal(['A',4,2], 1,1)
sage: [K.to_ambient_crystal()(b) for b in K]
[[], [[1, 1]], [[2, 2]], [[-2, -2]], [[-1, -1]]]
Bases: sage.combinat.crystals.affine.AffineCrystalFromClassicalElement
Class for the elements in the Kirillov-Reshetikhin crystals 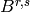 of type
of type 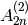 for
for 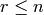 and type
and type 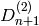 for
for 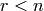 .
.
EXAMPLES:
sage: K=KirillovReshetikhinCrystal(['A',4,2],1,2)
sage: type(K.module_generators[0])
<class 'sage.combinat.crystals.kirillov_reshetikhin.KR_type_box_with_category.element_class'>
Gives 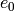 on self by mapping self to the ambient crystal, calculating
on self by mapping self to the ambient crystal, calculating 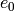 there and
pulling the element back.
there and
pulling the element back.
EXAMPLES:
sage: K=KirillovReshetikhinCrystal(['A',4,2],1,1)
sage: b = K(rows=[])
sage: b.e(0)
[[-1]]
Calculates 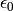 of self by mapping the element to the ambient crystal
and calculating
of self by mapping the element to the ambient crystal
and calculating 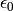 there.
there.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['A',4,2], 1,1)
sage: b=K(rows=[[1]])
sage: b.epsilon(0)
2
Gives 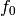 on self by mapping self to the ambient crystal, calculating
on self by mapping self to the ambient crystal, calculating 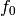 there and
pulling the element back.
there and
pulling the element back.
EXAMPLES:
sage: K=KirillovReshetikhinCrystal(['A',4,2],1,1)
sage: b = K(rows=[])
sage: b.f(0)
[[1]]
Calculates 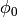 of self by mapping the element to the ambient crystal
and calculating
of self by mapping the element to the ambient crystal
and calculating 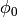 there.
there.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['D',3,2], 1,1)
sage: b=K(rows=[[-1]])
sage: b.phi(0)
2
Bases: sage.combinat.crystals.kirillov_reshetikhin.KirillovReshetikhinCrystalFromPromotion
Class of Kirillov-Reshetikhin crystals 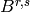 of type
of type 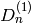 for
for 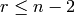 ,
,
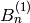 for
for 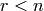 , and
, and 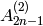 for
for 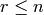 .
.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['D',4,1], 2,2)
sage: b = K(rows=[])
sage: b.f(0)
[[1], [2]]
sage: b.f(0).f(0)
[[1, 1], [2, 2]]
sage: b.e(0)
[[-2], [-1]]
sage: b.e(0).e(0)
[[-2, -2], [-1, -1]]
sage: K = KirillovReshetikhinCrystal(['B',3,1], 1,1)
sage: [[b,b.f(0)] for b in K]
[[[[1]], None], [[[2]], None], [[[3]], None], [[[0]], None], [[[-3]], None], [[[-2]], [[1]]], [[[-1]], [[2]]]]
sage: K = KirillovReshetikhinCrystal(['A',5,2], 1,1)
sage: [[b,b.f(0)] for b in K]
[[[[1]], None], [[[2]], None], [[[3]], None], [[[-3]], None], [[[-2]], [[1]]], [[[-1]], [[2]]]]
Specifies the classical crystal underlying the Kirillov-Reshetikhin crystal of type 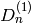 ,
,
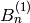 , and
, and 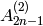 .
It is given by
.
It is given by 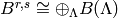 where
where 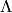 are weights obtained from
a rectangle of width s and height r by removing verticle dominoes. Here we identify the fundamental
weight
are weights obtained from
a rectangle of width s and height r by removing verticle dominoes. Here we identify the fundamental
weight 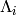 with a column of height
with a column of height  .
.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['D',4,1], 2,2)
sage: K.classical_decomposition()
The crystal of tableaux of type ['D', 4] and shape(s) [[], [1, 1], [2, 2]]
Specifies the Dynkin diagram automorphism underlying the promotion action on the crystal elements. The automorphism needs to map node 0 to some other Dynkin node.
Here we use the Dynkin diagram automorphism which interchanges nodes 0 and 1 and leaves all other nodes unchanged.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['D',4,1],1,1)
sage: K.dynkin_diagram_automorphism(0)
1
sage: K.dynkin_diagram_automorphism(1)
0
sage: K.dynkin_diagram_automorphism(4)
4
This gives the bijection between an element b in the classical decomposition
of the KR crystal that is 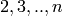 -highest weight and
-highest weight and 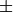 diagrams.
diagrams.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['D',4,1], 2,2)
sage: T = K.classical_decomposition()
sage: b = T(rows=[[2],[-2]])
sage: pm = K.from_highest_weight_vector_to_pm_diagram(b); pm
[[1, 1], [0, 0], [0]]
sage: pm.__repr__(pretty_printing=True)
+
-
sage: b = T(rows=[])
sage: pm=K.from_highest_weight_vector_to_pm_diagram(b); pm
[[0, 2], [0, 0], [0]]
sage: pm.__repr__(pretty_printing=True)
sage: hw = [ b for b in T if all(b.epsilon(i)==0 for i in [2,3,4]) ]
sage: all(K.from_pm_diagram_to_highest_weight_vector(K.from_highest_weight_vector_to_pm_diagram(b)) == b for b in hw)
True
This gives the bijection between a 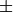 diagram and an element b in the classical
decomposition of the KR crystal that is {2,3,..,n}-highest weight.
diagram and an element b in the classical
decomposition of the KR crystal that is {2,3,..,n}-highest weight.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['D',4,1], 2,2)
sage: pm = sage.combinat.crystals.kirillov_reshetikhin.PMDiagram([[1, 1], [0, 0], [0]])
sage: K.from_pm_diagram_to_highest_weight_vector(pm)
[[2], [-2]]
Specifies the promotion operator used to construct the affine type 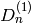 etc. crystal.
This corresponds to the Dynkin diagram automorphism which interchanges nodes 0 and 1,
and leaves all other nodes unchanged. On the level of crystals it is constructed using
etc. crystal.
This corresponds to the Dynkin diagram automorphism which interchanges nodes 0 and 1,
and leaves all other nodes unchanged. On the level of crystals it is constructed using
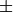 diagrams.
diagrams.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal([‘D’,4,1], 2,2) sage: promotion = K.promotion() sage: b = K.classical_decomposition()(rows=[]) sage: promotion(b) [[1, 2], [-2, -1]] sage: b = K.classical_decomposition()(rows=[[1,3],[2,-1]]) sage: promotion(b) [[1, 3], [2, -1]] sage: b = K.classical_decomposition()(rows=[[1],[-3]]) sage: promotion(b) [[2, -3], [-2, -1]]
Specifies the promotion operator used to construct the affine type 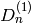 etc. crystal.
This corresponds to the Dynkin diagram automorphism which interchanges nodes 0 and 1,
and leaves all other nodes unchanged. On the level of crystals it is constructed using
etc. crystal.
This corresponds to the Dynkin diagram automorphism which interchanges nodes 0 and 1,
and leaves all other nodes unchanged. On the level of crystals it is constructed using
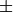 diagrams.
diagrams.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal([‘D’,4,1], 2,2) sage: promotion = K.promotion() sage: b = K.classical_decomposition()(rows=[]) sage: promotion(b) [[1, 2], [-2, -1]] sage: b = K.classical_decomposition()(rows=[[1,3],[2,-1]]) sage: promotion(b) [[1, 3], [2, -1]] sage: b = K.classical_decomposition()(rows=[[1],[-3]]) sage: promotion(b) [[2, -3], [-2, -1]]
Calculates promotion on 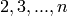 highest weight vectors.
highest weight vectors.
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['D',4,1], 2,2)
sage: T = K.classical_decomposition()
sage: hw = [ b for b in T if all(b.epsilon(i)==0 for i in [2,3,4]) ]
sage: [K.promotion_on_highest_weight_vectors()(b) for b in hw]
[[[1, 2], [-2, -1]], [[2, 2], [-2, -1]], [[1, 2], [3, -1]], [[2], [-2]],
[[1, 2], [2, -2]], [[2, 2], [-1, -1]], [[2, 2], [3, -1]], [[2, 2], [3, 3]],
[], [[1], [2]], [[1, 1], [2, 2]], [[2], [-1]], [[1, 2], [2, -1]], [[2], [3]],
[[1, 2], [2, 3]]]
Returns the Kirillov-Reshetikhin crystal 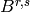 of the given type.
of the given type.
For more information about general crystals see sage.combinat.crystals.
Many Kirillov-Reshetikhin crystals are constructed from a
classical crystal together with an automorphism  on the level of crystals which
corresponds to a Dynkin diagram automorphism mapping node 0 to some other node i.
The action of
on the level of crystals which
corresponds to a Dynkin diagram automorphism mapping node 0 to some other node i.
The action of 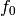 and
and 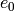 is then constructed using
is then constructed using
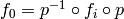 .
.
For example, for type 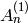 the Kirillov-Reshetikhin crystal
the Kirillov-Reshetikhin crystal 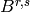 is obtained from the classical crystal
is obtained from the classical crystal 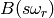 using the
promotion operator. For other types, see
using the
promotion operator. For other types, see
M. Shimozono “Affine type A crystal structure on tensor products of rectangles, Demazure characters, and nilpotent varieties”, J. Algebraic Combin. 15 (2002), no. 2, 151-187 (arXiv:math.QA/9804039)
A. Schilling, “Combinatorial structure of Kirillov-Reshetikhin crystals of
type 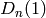 ,
, 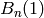 ,
, 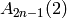 “, J. Algebra 319 (2008) 2938-2962
(arXiv:0704.2046 [math.QA])
“, J. Algebra 319 (2008) 2938-2962
(arXiv:0704.2046 [math.QA])
B. Jones, A. Schilling,
“”Affine structures and a tableau model for 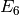 crystals”,
preprint arXiv:0909.2442 [math.CO]
crystals”,
preprint arXiv:0909.2442 [math.CO]
Other Kirillov-Reshetikhin crystals are constructed using similarity methods. See Section 4 of
G. Fourier, M. Okado, A. Schilling, “Kirillov-Reshetikhin crystals for nonexceptional types”, Advances in Mathematics 222 Issue 3 (2009) 1080-1116 (arXiv:0810.5067 [math.RT])
INPUT:
- cartan_type Affine type and rank
- r Label of finite Dynkin diagram
- s Positive integer
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['A',3,1], 2, 1)
sage: K.index_set()
[0, 1, 2, 3]
sage: K.list()
[[[1], [2]], [[1], [3]], [[2], [3]], [[1], [4]], [[2], [4]], [[3], [4]]]
sage: b=K(rows=[[1],[2]])
sage: b.weight()
-Lambda[0] + Lambda[2]
sage: K = KirillovReshetikhinCrystal(['A',3,1], 2,2)
sage: K.automorphism(K.module_generators[0])
[[2, 2], [3, 3]]
sage: K.module_generators[0].e(0)
[[1, 2], [2, 4]]
sage: K.module_generators[0].f(2)
[[1, 1], [2, 3]]
sage: K.module_generators[0].f(1)
sage: K.module_generators[0].phi(0)
0
sage: K.module_generators[0].phi(1)
0
sage: K.module_generators[0].phi(2)
2
sage: K.module_generators[0].epsilon(0)
2
sage: K.module_generators[0].epsilon(1)
0
sage: K.module_generators[0].epsilon(2)
0
sage: b = K(rows=[[1,2],[2,3]])
sage: b
[[1, 2], [2, 3]]
sage: b.f(2)
[[1, 2], [3, 3]]
sage: K = KirillovReshetikhinCrystal(['D',4,1], 2, 1)
sage: K.cartan_type()
['D', 4, 1]
sage: type(K.module_generators[0])
<class 'sage.combinat.crystals.affine.KR_type_vertical_with_category.element_class'>
Bases: sage.combinat.crystals.kirillov_reshetikhin.KirillovReshetikhinGenericCrystal, sage.combinat.crystals.affine.AffineCrystalFromClassicalAndPromotion
This generic class assumes that the Kirillov-Reshetikhin crystal is constructed from a classical crystal ‘classical_decomposition’ and an automorphism ‘promotion’ and its inverse which corresponds to a Dynkin diagram automorphism ‘dynkin_diagram_automorphism’.
Each instance using this class needs to implement the methods: - classical_decomposition - promotion - promotion_inverse - dynkin_diagram_automorphism
Bases: sage.structure.parent.Parent
Generic class for Kirillov-Reshetikhin crystal 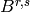 of the given type.
of the given type.
Input is a Dynkin node  , a positive integer
, a positive integer  , and a Cartan type
, and a Cartan type 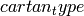 .
.
INPUT:
- self – a crystal
- K – a Kirillov-Reshetikhin crystal of the same type as
.
Returns the combinatorial `R`-matrix from 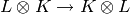 , where the combinatorial
, where the combinatorial  -matrix is the affine
crystal isomorphism which maps
-matrix is the affine
crystal isomorphism which maps 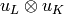 to
to 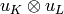 , where
, where 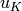 is the unique element in
is the unique element in 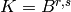 of weight
of weight 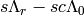 (see
module_generator).
(see
module_generator).
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['A',2,1],1,1)
sage: L = KirillovReshetikhinCrystal(['A',2,1],1,2)
sage: f = K.R_matrix(L)
sage: [[b,f(b)] for b in TensorProductOfCrystals(K,L)]
[[[[[1]], [[1, 1]]], [[[1, 1]], [[1]]]],
[[[[1]], [[1, 2]]], [[[1, 1]], [[2]]]],
[[[[1]], [[2, 2]]], [[[1, 2]], [[2]]]],
[[[[1]], [[1, 3]]], [[[1, 1]], [[3]]]],
[[[[1]], [[2, 3]]], [[[1, 2]], [[3]]]],
[[[[1]], [[3, 3]]], [[[1, 3]], [[3]]]],
[[[[2]], [[1, 1]]], [[[1, 2]], [[1]]]],
[[[[2]], [[1, 2]]], [[[2, 2]], [[1]]]],
[[[[2]], [[2, 2]]], [[[2, 2]], [[2]]]],
[[[[2]], [[1, 3]]], [[[2, 3]], [[1]]]],
[[[[2]], [[2, 3]]], [[[2, 2]], [[3]]]],
[[[[2]], [[3, 3]]], [[[2, 3]], [[3]]]],
[[[[3]], [[1, 1]]], [[[1, 3]], [[1]]]],
[[[[3]], [[1, 2]]], [[[1, 3]], [[2]]]],
[[[[3]], [[2, 2]]], [[[2, 3]], [[2]]]],
[[[[3]], [[1, 3]]], [[[3, 3]], [[1]]]],
[[[[3]], [[2, 3]]], [[[3, 3]], [[2]]]],
[[[[3]], [[3, 3]]], [[[3, 3]], [[3]]]]]
sage: K = KirillovReshetikhinCrystal(['D',4,1],1,1)
sage: L = KirillovReshetikhinCrystal(['D',4,1],2,1)
sage: f = K.R_matrix(L)
sage: T = TensorProductOfCrystals(K,L)
sage: b = T( K(rows=[[1]]), L(rows=[]) )
sage: f(b)
[[[2], [-2]], [[1]]]
Yields the module generator of weight 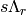 of a Kirillov-Reshetikhin crystal
of a Kirillov-Reshetikhin crystal 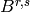
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['C',2,1],1,2)
sage: K.module_generator()
[[1, 1]]
sage: K = KirillovReshetikhinCrystal(['E',6,1],1,1)
sage: K.module_generator()
[[1]]
sage: K = KirillovReshetikhinCrystal(['D',4,1],2,1)
sage: K.module_generator()
[[1], [2]]
Returns r of the underlying Kirillov-Reshetikhin crystal 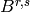
EXAMPLE:
sage: K = KirillovReshetikhinCrystal(['D',4,1], 2, 1)
sage: K.r()
2
Returns s of the underlying Kirillov-Reshetikhin crystal 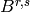
EXAMPLE:
sage: K = KirillovReshetikhinCrystal(['D',4,1], 2, 1)
sage: K.s()
1
Bases: sage.combinat.combinat.CombinatorialObject
Class of 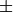 diagrams. These diagrams are in one-to-one bijection with
diagrams. These diagrams are in one-to-one bijection with 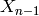 highest weight vectors
in an
highest weight vectors
in an 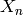 highest weight crystal
highest weight crystal 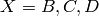 . See Section 4.1 of A. Schilling, “Combinatorial structure of
Kirillov-Reshetikhin crystals of type
. See Section 4.1 of A. Schilling, “Combinatorial structure of
Kirillov-Reshetikhin crystals of type 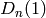 ,
, 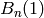 ,
, 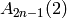 “, J. Algebra 319 (2008) 2938-2962
(arXiv:0704.2046[math.QA]).
“, J. Algebra 319 (2008) 2938-2962
(arXiv:0704.2046[math.QA]).
The input is a list ![pm = [[a_0,b_0],[a_1,b_1],...,[a_{n-1},b_{n-1}],[b_n]]](../../../_images/math/359d2cdefccfcbfb128372a5dc8c1ef040de11cc.png) of 2-tuples and a last 1-tuple.
The tuple
of 2-tuples and a last 1-tuple.
The tuple ![[a_i,b_i]](../../../_images/math/f92102dde7c02218b6f7b5cfc7758a3c7ef20e03.png) specifies the number of
specifies the number of 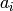 + and
+ and 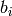 - in the i-th row of the pm diagram
if
- in the i-th row of the pm diagram
if 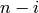 is odd and the number of
is odd and the number of 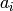 +- pairs above row
+- pairs above row  and
and 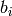 columns of height
columns of height  not containing
any + or - if
not containing
any + or - if 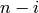 is even.
is even.
Setting the option ‘from_shapes = True’ one can also input a 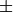 diagram in terms of its
outer, intermediate and inner shape by specifying a tuple [n, s, outer, intermediate, inner]
where
diagram in terms of its
outer, intermediate and inner shape by specifying a tuple [n, s, outer, intermediate, inner]
where  is the width of the
is the width of the 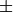 diagram, and ‘outer’ , ‘intermediate’,
and ‘inner’ are the outer, intermediate and inner shape, respectively.
diagram, and ‘outer’ , ‘intermediate’,
and ‘inner’ are the outer, intermediate and inner shape, respectively.
EXAMPLES:
sage: pm=sage.combinat.crystals.kirillov_reshetikhin.PMDiagram([[0,1],[1,2],[1]])
sage: pm.pm_diagram
[[0, 1], [1, 2], [1]]
sage: pm._list
[1, 1, 2, 0, 1]
sage: pm.n
2
sage: pm.width
5
sage: pm.__repr__(pretty_printing=True)
. . . .
. + - -
sage: sage.combinat.crystals.kirillov_reshetikhin.PMDiagram([2,5,[4,4],[4,2],[4,1]], from_shapes=True)
[[0, 1], [1, 2], [1]]
TESTS:
sage: pm=sage.combinat.crystals.kirillov_reshetikhin.PMDiagram([[1,2],[1,1],[1,1],[1,1],[1]])
sage: sage.combinat.crystals.kirillov_reshetikhin.PMDiagram([pm.n, pm.width, pm.outer_shape(), pm.intermediate_shape(), pm.inner_shape()], from_shapes=True) == pm
True
sage: pm=sage.combinat.crystals.kirillov_reshetikhin.PMDiagram([[1,2],[1,2],[1,1],[1,1],[1,1],[1]])
sage: sage.combinat.crystals.kirillov_reshetikhin.PMDiagram([pm.n, pm.width, pm.outer_shape(), pm.intermediate_shape(), pm.inner_shape()], from_shapes=True) == pm
True
Returns a list with the heights of all addable plus in the 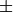 diagram.
diagram.
EXAMPLES:
sage: pm=sage.combinat.crystals.kirillov_reshetikhin.PMDiagram([[1,2],[1,2],[1,1],[1,1],[1,1],[1]])
sage: pm.heights_of_addable_plus()
[1, 1, 2, 3, 4, 5]
sage: pm=sage.combinat.crystals.kirillov_reshetikhin.PMDiagram([[1,2],[1,1],[1,1],[1,1],[1]])
sage: pm.heights_of_addable_plus()
[1, 2, 3, 4]
Returns a list with the heights of all minus in the 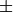 diagram.
diagram.
EXAMPLES:
sage: pm=sage.combinat.crystals.kirillov_reshetikhin.PMDiagram([[1,2],[1,2],[1,1],[1,1],[1,1],[1]])
sage: pm.heights_of_minus()
[5, 5, 3, 3, 1, 1]
sage: pm=sage.combinat.crystals.kirillov_reshetikhin.PMDiagram([[1,2],[1,1],[1,1],[1,1],[1]])
sage: pm.heights_of_minus()
[4, 4, 2, 2]
Returns the inner shape of the pm diagram
Returns the intermediate shape of the pm diagram (innner shape plus positions of plusses)
EXAMPLES:
sage: pm=sage.combinat.crystals.kirillov_reshetikhin.PMDiagram([[0,1],[1,2],[1]])
sage: pm.intermediate_shape()
[4, 2]
sage: pm=sage.combinat.crystals.kirillov_reshetikhin.PMDiagram([[1,2],[1,1],[1,1],[1,1],[1]])
sage: pm.intermediate_shape()
[8, 6, 4, 2]
sage: pm=sage.combinat.crystals.kirillov_reshetikhin.PMDiagram([[1,2],[1,2],[1,1],[1,1],[1,1],[1]])
sage: pm.intermediate_shape()
[11, 8, 6, 4, 2]
sage: pm=sage.combinat.crystals.kirillov_reshetikhin.PMDiagram([[1,0],[0,1],[2,0],[0,0],[0]])
sage: pm.intermediate_shape()
[4, 2, 2]
Returns the outer shape of the pm diagram
EXAMPLES:
sage: pm=sage.combinat.crystals.kirillov_reshetikhin.PMDiagram([[0,1],[1,2],[1]])
sage: pm.outer_shape()
[4, 4]
sage: pm=sage.combinat.crystals.kirillov_reshetikhin.PMDiagram([[1,2],[1,1],[1,1],[1,1],[1]])
sage: pm.outer_shape()
[8, 8, 4, 4]
sage: pm=sage.combinat.crystals.kirillov_reshetikhin.PMDiagram([[1,2],[1,2],[1,1],[1,1],[1,1],[1]])
sage: pm.outer_shape()
[13, 8, 8, 4, 4]
Returns sigma on pm diagrams as needed for the analogue of the Dynkin diagram automorphism
that interchanges nodes  and
and  for type
for type 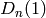 ,
, 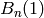 ,
, 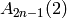 for
Kirillov-Reshetikhin crystals.
for
Kirillov-Reshetikhin crystals.
EXAMPLES:
sage: pm=sage.combinat.crystals.kirillov_reshetikhin.PMDiagram([[0,1],[1,2],[1]])
sage: pm.sigma().pm_diagram
[[1, 0], [2, 1], [1]]
Returns all partitions obtained from a rectangle of width s and height r by removing horizontal dominoes.
EXAMPLES:
sage: sage.combinat.crystals.kirillov_reshetikhin.horizontal_dominoes_removed(2,2)
[[], [2], [2, 2]]
sage: sage.combinat.crystals.kirillov_reshetikhin.horizontal_dominoes_removed(3,2)
[[], [2], [2, 2], [2, 2, 2]]
Returns all partitions in a box of width s and height r.
EXAMPLES:
sage: sage.combinat.crystals.kirillov_reshetikhin.partitions_in_box(3,2)
[[], [1], [2], [1, 1], [2, 1], [1, 1, 1], [2, 2], [2, 1, 1],
[2, 2, 1], [2, 2, 2]]
Returns all partitions obtained from a rectangle of width s and height r by removing vertical dominoes.
EXAMPLES:
sage: sage.combinat.crystals.kirillov_reshetikhin.vertical_dominoes_removed(2,2)
[[], [1, 1], [2, 2]]
sage: sage.combinat.crystals.kirillov_reshetikhin.vertical_dominoes_removed(3,2)
[[2], [2, 1, 1], [2, 2, 2]]
sage: sage.combinat.crystals.kirillov_reshetikhin.vertical_dominoes_removed(4,2)
[[], [1, 1], [1, 1, 1, 1], [2, 2], [2, 2, 1, 1], [2, 2, 2, 2]]