Highest weight crystals

class sage.combinat.crystals.highest_weight_crystals.FiniteDimensionalHighestWeightCrystal_TypeE(dominant_weight)

Bases: sage.combinat.crystals.tensor_product.CrystalOfWords

Commonalities for all finite dimensional type E highest weight crystals

Subclasses should setup an attribute column_crystal in their __init__ method before calling the __init__ method of this class.

module_generator()

This yields the module generator (or highest weight element) of the classical crystal of given dominant weight in self.

EXAMPLES:

sage: C=CartanType(['E',6])
sage: La=C.root_system().weight_lattice().fundamental_weights()
sage: T = HighestWeightCrystal(La[2])
sage: T.module_generator()
[[[2, -1], [1]]]
sage: T = HighestWeightCrystal(0*La[2])
sage: T.module_generator()
[]

sage: C=CartanType(['E',7])
sage: La=C.root_system().weight_lattice().fundamental_weights()
sage: T = HighestWeightCrystal(La[1])
sage: T.module_generator()
[[[-7, 1], [7]]]

class sage.combinat.crystals.highest_weight_crystals.FiniteDimensionalHighestWeightCrystal_TypeE6(dominant_weight)

Bases: sage.combinat.crystals.highest_weight_crystals.FiniteDimensionalHighestWeightCrystal_TypeE

Class of finite dimensional highest weight crystals of type .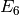

EXAMPLES:

sage: C=CartanType(['E',6])
sage: La=C.root_system().weight_lattice().fundamental_weights()
sage: T = HighestWeightCrystal(La[2]); T
Finite dimensional highest weight crystal of type ['E', 6] and highest weight Lambda[2]
sage: B2 = T.column_crystal[2]
sage: B2
The tensor product of the crystals (The crystal of letters for type ['E', 6] (dual), The crystal of letters for type ['E', 6])
sage: t = T(B2([]))
sage: t
[[[]]]
sage: TestSuite(t).run()
sage: t = T(B2([[-1],[-1,3]]))
sage: t
[[[[-1], [-1, 3]]]]
sage: TestSuite(t).run()

class sage.combinat.crystals.highest_weight_crystals.FiniteDimensionalHighestWeightCrystal_TypeE7(dominant_weight)

Bases: sage.combinat.crystals.highest_weight_crystals.FiniteDimensionalHighestWeightCrystal_TypeE

Class of finite dimensional highest weight crystals of type .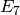

EXAMPLES:

sage: C=CartanType(['E',7])
sage: La=C.root_system().weight_lattice().fundamental_weights()
sage: T = HighestWeightCrystal(La[1])
sage: T.cardinality()
133
sage: B2 = T.column_crystal[2]
sage: B2
The tensor product of the crystals (The crystal of letters for type ['E', 7], The crystal of letters for type ['E', 7], The crystal of letters for type ['E', 7])
sage: t = T(B2([]))
sage: t
[[[]]]
sage: TestSuite(t).run()

sage.combinat.crystals.highest_weight_crystals.HighestWeightCrystal(dominant_weight)

Returns an implementation of the highest weight crystal of highest weight .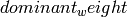

This is currently only implemented for crystals of type 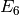and .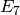

TODO: implement highest weight crystals for classical types 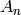, , 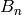, 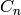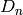using tableaux.

TODO: implement the Littelmann path model or alcove model to obtain a realization for any highest weight crystal of given type (even affine).

EXAMPLES:

sage: C=CartanType(['E',6])
sage: La=C.root_system().weight_lattice().fundamental_weights()
sage: T = HighestWeightCrystal(La[1])
sage: T.cardinality()
27
sage: T = HighestWeightCrystal(La[6])
sage: T.cardinality()
27
sage: T = HighestWeightCrystal(La[2])
sage: T.cardinality()
78
sage: T = HighestWeightCrystal(La[4])
sage: T.cardinality()
2925
sage: T = HighestWeightCrystal(La[3])
sage: T.cardinality()
351
sage: T = HighestWeightCrystal(La[5])
sage: T.cardinality()
351

sage: C=CartanType(['E',7])
sage: La=C.root_system().weight_lattice().fundamental_weights()
sage: T = HighestWeightCrystal(La[1])
sage: T.cardinality()
133
sage: T = HighestWeightCrystal(La[2])
sage: T.cardinality()
912
sage: T = HighestWeightCrystal(La[3])
sage: T.cardinality()
8645
sage: T = HighestWeightCrystal(La[4])
sage: T.cardinality()
365750
sage: T = HighestWeightCrystal(La[5])
sage: T.cardinality()
27664
sage: T = HighestWeightCrystal(La[6])
sage: T.cardinality()
1539
sage: T = HighestWeightCrystal(La[7])
sage: T.cardinality()
56