Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Combinatorics »
- Crystals »

Bases: sage.structure.unique_representation.UniqueRepresentation, sage.structure.parent.Parent
This abstract class can be used for affine crystals that are constructed from a classical crystal. The zero arrows can be implemented using different methods (for example using a Dynkin diagram automorphisms or virtual crystals).
This is a helper class, mostly used to implement Kirillov-Reshetikhin crystals (see: sage.combinat.crystals.kirillov_reshetikhin.KirillovReshetikhin()).
For general information about crystals see sage.combinat.crystals.
INPUT:
EXAMPLES:
sage: n=2
sage: C=CrystalOfTableaux(['A',n],shape=[1])
sage: pr = attrcall("promotion")
sage: pr_inverse = attrcall("promotion_inverse")
sage: A=AffineCrystalFromClassicalAndPromotion(['A',n,1],C,pr,pr_inverse,1)
sage: A.list()
[[[1]], [[2]], [[3]]]
sage: A.cartan_type()
['A', 2, 1]
sage: A.index_set()
[0, 1, 2]
sage: b=A(rows=[[1]])
sage: b.weight()
-Lambda[0] + Lambda[1]
sage: b.classical_weight()
(1, 0, 0)
sage: [x.s(0) for x in A.list()]
[[[3]], [[2]], [[1]]]
sage: [x.s(1) for x in A.list()]
[[[2]], [[1]], [[3]]]
Lifts an affine crystal element to the corresponding classical crystal element
EXAMPLES:
sage: n=2
sage: C=CrystalOfTableaux(['A',n],shape=[1])
sage: pr = attrcall("promotion")
sage: pr_inverse = attrcall("promotion_inverse")
sage: A=AffineCrystalFromClassicalAndPromotion(['A',n,1],C,pr,pr_inverse,1)
sage: b=A.list()[0]
sage: A.lift(b)
[[1]]
sage: A.lift(b).parent()
The crystal of tableaux of type ['A', 2] and shape(s) [[1]]
Returns the list of all crystal elements using the underlying classical crystal
EXAMPLES:
sage: n=2
sage: C=CrystalOfTableaux(['A',n],shape=[1])
sage: pr = attrcall("promotion")
sage: pr_inverse = attrcall("promotion_inverse")
sage: A=AffineCrystalFromClassicalAndPromotion(['A',n,1],C,pr,pr_inverse,1)
sage: A.list()
[[[1]], [[2]], [[3]]]
Transforms a classical crystal element to the corresponding affine crystal element
EXAMPLES:
sage: n=2
sage: C=CrystalOfTableaux(['A',n],shape=[1])
sage: pr = attrcall("promotion")
sage: pr_inverse = attrcall("promotion_inverse")
sage: A=AffineCrystalFromClassicalAndPromotion(['A',n,1],C,pr,pr_inverse,1)
sage: t=C(rows=[[1]])
sage: t.parent()
The crystal of tableaux of type ['A', 2] and shape(s) [[1]]
sage: A.retract(t)
[[1]]
sage: A.retract(t).parent() is A
True
Bases: sage.combinat.crystals.affine.AffineCrystalFromClassical
Crystals that are constructed from a classical crystal and a
Dynkin diagram automorphism 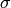 . In type
. In type 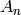 , the Dynkin
diagram automorphism is
, the Dynkin
diagram automorphism is 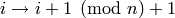 and the
corresponding map on the crystal is the promotion operation
and the
corresponding map on the crystal is the promotion operation
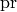 on tableaux. The affine crystal operators are given
by
on tableaux. The affine crystal operators are given
by 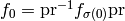 .
.
INPUT:
EXAMPLES:
sage: n=2
sage: C=CrystalOfTableaux(['A',n],shape=[1])
sage: pr = attrcall("promotion")
sage: pr_inverse = attrcall("promotion_inverse")
sage: A=AffineCrystalFromClassicalAndPromotion(['A',n,1],C,pr,pr_inverse,1)
sage: A.list()
[[[1]], [[2]], [[3]]]
sage: A.cartan_type()
['A', 2, 1]
sage: A.index_set()
[0, 1, 2]
sage: b=A(rows=[[1]])
sage: b.weight()
-Lambda[0] + Lambda[1]
sage: b.classical_weight()
(1, 0, 0)
sage: [x.s(0) for x in A.list()]
[[[3]], [[2]], [[1]]]
sage: [x.s(1) for x in A.list()]
[[[2]], [[1]], [[3]]]
Gives the analogue of the affine Dynkin diagram automorphism on the level of crystals
EXAMPLES:
sage: n=2
sage: C=CrystalOfTableaux(['A',n],shape=[1])
sage: pr = attrcall("promotion")
sage: pr_inverse = attrcall("promotion_inverse")
sage: A=AffineCrystalFromClassicalAndPromotion(['A',n,1],C,pr,pr_inverse,1)
sage: b=A.list()[0]
sage: A.automorphism(b)
[[2]]
Gives the analogue of the inverse of the affine Dynkin diagram automorphism on the level of crystals
EXAMPLES:
sage: n=2
sage: C=CrystalOfTableaux(['A',n],shape=[1])
sage: pr = attrcall("promotion")
sage: pr_inverse = attrcall("promotion_inverse")
sage: A=AffineCrystalFromClassicalAndPromotion(['A',n,1],C,pr,pr_inverse,1)
sage: b=A.list()[0]
sage: A.inverse_automorphism(b)
[[3]]
Bases: sage.combinat.crystals.affine.AffineCrystalFromClassicalElement
Elements of crystals that are constructed from a classical crystal and a Dynkin diagram automorphism. In type A, the automorphism is the promotion operation on tableaux.
This class is not instantiated directly but rather __call__ed from AffineCrystalFromClassicalAndPromotion. The syntax of this is governed by the (classical) CrystalOfTableaux.
Since this class inherits from AffineClassicalFromClassicalElement, the methods that need to be implemented are e0, f0 and possibly epsilon0 and phi0 if more efficient algorithms exist.
EXAMPLES:
sage: n=2
sage: C=CrystalOfTableaux(['A',n],shape=[1])
sage: pr = attrcall("promotion")
sage: pr_inverse = attrcall("promotion_inverse")
sage: A=AffineCrystalFromClassicalAndPromotion(['A',n,1],C,pr,pr_inverse,1)
sage: b=A(rows=[[1]])
sage: b._repr_()
'[[1]]'
Implements 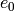 using the automorphism as
using the automorphism as
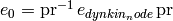
EXAMPLES:
sage: n=2
sage: C=CrystalOfTableaux(['A',n],shape=[1])
sage: pr = attrcall("promotion")
sage: pr_inverse = attrcall("promotion_inverse")
sage: A=AffineCrystalFromClassicalAndPromotion(['A',n,1],C,pr,pr_inverse,1)
sage: b=A(rows=[[1]])
sage: b.e0()
[[3]]
Implements 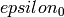 using the automorphism.
using the automorphism.
EXAMPLES:
sage: n=2
sage: C=CrystalOfTableaux(['A',n],shape=[1])
sage: pr = attrcall("promotion")
sage: pr_inverse = attrcall("promotion_inverse")
sage: A=AffineCrystalFromClassicalAndPromotion(['A',n,1],C,pr,pr_inverse,1)
sage: [x.epsilon0() for x in A.list()]
[1, 0, 0]
Implements 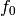 using the automorphism as
using the automorphism as
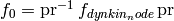
EXAMPLES:
sage: n=2
sage: C=CrystalOfTableaux(['A',n],shape=[1])
sage: pr = attrcall("promotion")
sage: pr_inverse = attrcall("promotion_inverse")
sage: A=AffineCrystalFromClassicalAndPromotion(['A',n,1],C,pr,pr_inverse,1)
sage: b=A(rows=[[3]])
sage: b.f0()
[[1]]
Implements 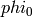 using the automorphism.
using the automorphism.
EXAMPLES:
sage: n=2
sage: C=CrystalOfTableaux(['A',n],shape=[1])
sage: pr = attrcall("promotion")
sage: pr_inverse = attrcall("promotion_inverse")
sage: A=AffineCrystalFromClassicalAndPromotion(['A',n,1],C,pr,pr_inverse,1)
sage: [x.phi0() for x in A.list()]
[0, 0, 1]
Bases: sage.structure.element_wrapper.ElementWrapper
Elements of crystals that are constructed from a classical crystal. The elements inherit many of their methods from the classical crystal using lift and retract.
This class is not instantiated directly but rather __call__ed from AffineCrystalFromClassical. The syntax of this is governed by the (classical) CrystalOfTableaux.
EXAMPLES:
sage: n=2
sage: C=CrystalOfTableaux(['A',n],shape=[1])
sage: pr = attrcall("promotion")
sage: pr_inverse = attrcall("promotion_inverse")
sage: A=AffineCrystalFromClassicalAndPromotion(['A',n,1],C,pr,pr_inverse,1)
sage: b=A(rows=[[1]])
sage: b._repr_()
'[[1]]'
Returns the classical weight corresponding to self.
EXAMPLES:
sage: n=2
sage: C=CrystalOfTableaux(['A',n],shape=[1])
sage: pr = attrcall("promotion")
sage: pr_inverse = attrcall("promotion_inverse")
sage: A=AffineCrystalFromClassicalAndPromotion(['A',n,1],C,pr,pr_inverse,1)
sage: b=A(rows=[[1]])
sage: b.classical_weight()
(1, 0, 0)
Returns the action of 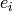 on self.
on self.
EXAMPLES:
sage: n=2
sage: C=CrystalOfTableaux(['A',n],shape=[1])
sage: pr = attrcall("promotion")
sage: pr_inverse = attrcall("promotion_inverse")
sage: A=AffineCrystalFromClassicalAndPromotion(['A',n,1],C,pr,pr_inverse,1)
sage: b=A(rows=[[1]])
sage: b.e(0)
[[3]]
sage: b.e(1)
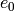 is implemented separately.
is implemented separately.Returns the maximal time the crystal operator 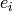 can be applied to self.
can be applied to self.
EXAMPLES:
sage: n=2
sage: C=CrystalOfTableaux(['A',n],shape=[1])
sage: pr = attrcall("promotion")
sage: pr_inverse = attrcall("promotion_inverse")
sage: A=AffineCrystalFromClassicalAndPromotion(['A',n,1],C,pr,pr_inverse,1)
sage: [x.epsilon(0) for x in A.list()]
[1, 0, 0]
sage: [x.epsilon(1) for x in A.list()]
[0, 1, 0]
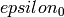 from the super class, but should be implemented if a faster implementation exists.
from the super class, but should be implemented if a faster implementation exists.Returns the action of 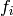 on self.
on self.
EXAMPLES:
sage: n=2
sage: C=CrystalOfTableaux(['A',n],shape=[1])
sage: pr = attrcall("promotion")
sage: pr_inverse = attrcall("promotion_inverse")
sage: A=AffineCrystalFromClassicalAndPromotion(['A',n,1],C,pr,pr_inverse,1)
sage: b=A(rows=[[3]])
sage: b.f(0)
[[1]]
sage: b.f(2)
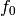 is implemented separately.
is implemented separately.Lifts an affine crystal element to the corresponding classical crystal element
EXAMPLES:
sage: n=2
sage: C=CrystalOfTableaux(['A',n],shape=[1])
sage: pr = attrcall("promotion")
sage: pr_inverse = attrcall("promotion_inverse")
sage: A=AffineCrystalFromClassicalAndPromotion(['A',n,1],C,pr,pr_inverse,1)
sage: b=A.list()[0]
sage: b.lift()
[[1]]
sage: b.lift().parent()
The crystal of tableaux of type ['A', 2] and shape(s) [[1]]
Returns the maximal time the crystal operator 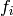 can be applied to self.
can be applied to self.
EXAMPLES:
sage: n=2
sage: C=CrystalOfTableaux(['A',n],shape=[1])
sage: pr = attrcall("promotion")
sage: pr_inverse = attrcall("promotion_inverse")
sage: A=AffineCrystalFromClassicalAndPromotion(['A',n,1],C,pr,pr_inverse,1)
sage: [x.phi(0) for x in A.list()]
[0, 0, 1]
sage: [x.phi(1) for x in A.list()]
[1, 0, 0]
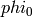 from the super class, but should be implemented if a faster implementation exists.
from the super class, but should be implemented if a faster implementation exists.Method for pretty printing
EXAMPLES:
sage: K = KirillovReshetikhinCrystal(['D',3,2],1,1)
sage: t=K(rows=[[1]])
sage: t.pp()
1