Examples of finite Weyl groups

sage.categories.examples.finite_weyl_groups.Example

alias of SymmetricGroup

class sage.categories.examples.finite_weyl_groups.SymmetricGroup(n=4)

Bases: sage.structure.unique_representation.UniqueRepresentation, sage.structure.parent.Parent

An example of finite Weyl group: the symmetric group, with elements in list notation.

The purpose of this class is to provide a minimal template for implementing finite Weyl groups. See SymmetricGroup for a full featured and optimized implementation.

EXAMPLES:

sage: S = FiniteWeylGroups().example()
sage: S
The symmetric group on {0, ..., 3}
sage: S.category()
Category of finite weyl groups

The elements of this group are permutations of the set :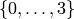

sage: S.one()
(0, 1, 2, 3)
sage: S.an_element()
(1, 2, 3, 0)

The group itself is generated by the elementary transpositions:

sage: S.simple_reflections()
Finite family {0: (1, 0, 2, 3), 1: (0, 2, 1, 3), 2: (0, 1, 3, 2)}

TESTS:

sage: TestSuite(S).run(verbose = True)
running ._test_an_element() . . . pass
running ._test_associativity() . . . pass
running ._test_category() . . . pass
running ._test_elements() . . .
  Running the test suite of self.an_element()
  running ._test_category() . . . pass
  running ._test_eq() . . . pass
  running ._test_not_implemented_methods() . . . pass
  running ._test_pickling() . . . pass
  pass
running ._test_elements_eq() . . . pass
running ._test_enumerated_set_contains() . . . pass
running ._test_enumerated_set_iter_cardinality() . . . pass
running ._test_enumerated_set_iter_list() . . . pass
running ._test_eq() . . . pass
running ._test_has_descent() . . . pass
running ._test_inverse() . . . pass
running ._test_not_implemented_methods() . . . pass
running ._test_one() . . . pass
running ._test_pickling() . . . pass
running ._test_prod() . . . pass
running ._test_reduced_word() . . . pass
running ._test_simple_projections() . . . pass
running ._test_some_elements() . . . pass

Only the following basic operations are implemented:

• one()
• product()
• simple_reflection()
• Element.has_right_descent().

All the other usual Weyl group operations are inherited from the categories:

sage: S.cardinality()
24
sage: S.long_element()
(3, 2, 1, 0)
sage: S.cayley_graph(side = "left").plot()

Alternatively, one could have implemented apply_simple_reflection() instead of simple_reflection() and product(). See CoxeterGroups().example().

class Element(value, parent)

Bases: sage.structure.element_wrapper.ElementWrapper

has_right_descent(i)

Implements CoxeterGroups.ElementMethods.has_right_descent().

EXAMPLES:

sage: S = FiniteWeylGroups().example()
sage: s = S.simple_reflections()
sage: (s[1] * s[2]).has_descent(2)
True
sage: S._test_has_descent()

SymmetricGroup.an_element(*args, **kwds)

Implements: Sets.ParentMethods.an_element() by returning the product of the simple reflections (a Coxeter element).

EXAMPLES:

sage: W=CoxeterGroups().example()
sage: W
The symmetric group on {0, ..., 3}
sage: W.an_element()
(1, 2, 3, 0)

SymmetricGroup.index_set()

Implements CoxeterGroups.ParentMethods.index_set().

EXAMPLES:

sage: FiniteWeylGroups().example().index_set()
[0, 1, 2]

SymmetricGroup.one(*args, **kwds)

Implements Monoids.ParentMethods.one().

EXAMPLES:

sage: FiniteWeylGroups().example().one()
(0, 1, 2, 3)

SymmetricGroup.product(x, y)

Implements Semigroups.ParentMethods.product().

EXAMPLES:

sage: s = FiniteWeylGroups().example().simple_reflections()
sage: s[1] * s[2]
(0, 2, 3, 1)

SymmetricGroup.simple_reflection(i)

Implements CoxeterGroups.ParentMethods.simple_reflection() by returning the transposition .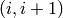

EXAMPLES:

sage: FiniteWeylGroups().example().simple_reflection(2)
(0, 1, 3, 2)