You can construct the following permutation groups:
 of order
of order 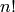 (n can also be a list
(n can also be a list  of distinct
of distinct 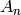 or order
or order 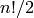 (n can also be a list
(n can also be a list 
– DihedralGroup, 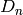 of order
of order 
– CyclicPermutationGroup, 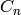 of order
of order 
– DiCyclicGroup, nonabelian groups of order 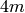 with a unique element of order 2
with a unique element of order 2
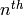 transitive group of degree
transitive group of degree 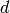
– TransitiveGroups(d), TransitiveGroups(), set of all of the above
– MathieuGroup(degree), Mathieu group of degree 9, 10, 11, 12, 21, 22, 23, or 24.
– KleinFourGroup, subgroup of 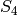 of order
of order 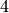 which is not
which is not 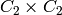
– QuaternionGroup, non-abelian group of order 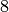 ,
, 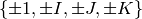
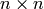 matrices over
matrices over 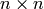 matrices over
matrices over 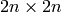 matrices
matrices 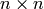 matrices having
matrices having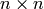 matrices having
matrices having– SuzukiGroup(q), Suzuki group over GF(q), 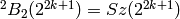 .
.
Bases: sage.groups.perm_gps.permgroup_named.PermutationGroup_unique
Returns the corresponding Abelian Group instance.
Return True if this group is abelian.
Return True if this group is commutative.
Bases: sage.groups.perm_gps.permgroup_named.PermutationGroup_unique
The dicyclic group of order 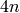 , for
, for 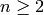 .
.
OUTPUT:
This is a nonabelian group similar in some respects to the dihedral group of the same order, but with far fewer elements of order 2 (it has just one). The permutation representation constructed here is based on the presentation
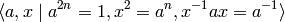
For  this is the group of quaternions
(
this is the group of quaternions
(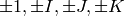 ), which is the nonabelian
group of order 8 that is not the dihedral group
), which is the nonabelian
group of order 8 that is not the dihedral group 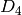 ,
the symmetries of a square. For
,
the symmetries of a square. For  this is the nonabelian
group of order 12 that is not the dihedral group
this is the nonabelian
group of order 12 that is not the dihedral group  nor the alternating group
nor the alternating group 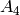 . This group of order 12 is
also the semi-direct product of of
. This group of order 12 is
also the semi-direct product of of 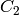 by
by  ,
,
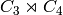 . [CONRAD2009]
. [CONRAD2009]
When the order of the group is a power of 2 it is known as a “generalized quaternion group.”
IMPLEMENTATION:
The presentation above means every element can be written as
 with
with  ,
, 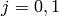 . We code
. We code 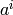 as the symbol
as the symbol
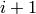 and code
and code  as the symbol
as the symbol 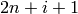 . The two generators
are then represented using a left regular representation.
. The two generators
are then represented using a left regular representation.
EXAMPLES:
A dicyclic group of order 384, with a large power of 2 as a divisor:
sage: n = 3*2^5
sage: G = DiCyclicGroup(n)
sage: G.order()
384
sage: a = G.gen(0)
sage: x = G.gen(1)
sage: a^(2*n)
()
sage: a^n==x^2
True
sage: x^-1*a*x==a^-1
True
A large generalized quaternion group (order is a power of 2):
sage: n = 2^10
sage: G=DiCyclicGroup(n)
sage: G.order()
4096
sage: a = G.gen(0)
sage: x = G.gen(1)
sage: a^(2*n)
()
sage: a^n==x^2
True
sage: x^-1*a*x==a^-1
True
Just like the dihedral group, the dicyclic group has an element whose order is half the order of the group. Unlike the dihedral group, the dicyclic group has only one element of order 2. Like the dihedral groups of even order, the center of the dicyclic group is a subgroup of order 2 (thus has the unique element of order 2 as its non-identity element).
sage: G=DiCyclicGroup(3*5*4)
sage: G.order()
240
sage: two = [g for g in G if g.order()==2]; two
[(1,5)(2,6)(3,7)(4,8)(9,13)(10,14)(11,15)(12,16)]
sage: G.center().order()
2
For small orders, we check this is really a group we do not have in Sage otherwise.
sage: G = DiCyclicGroup(2)
sage: H = DihedralGroup(4)
sage: G.is_isomorphic(H)
False
sage: G = DiCyclicGroup(3)
sage: H = DihedralGroup(6)
sage: K = AlternatingGroup(6)
sage: G.is_isomorphic(H) or G.is_isomorphic(K)
False
REFERENCES:
[CONRAD2009] Groups of order 12. Keith Conrad, accessed 21 October 2009.
Return True if this group is abelian.
EXAMPLES:
sage: D = DiCyclicGroup(12)
sage: D.is_abelian()
False
Return True if this group is commutative.
EXAMPLES:
sage: D = DiCyclicGroup(12)
sage: D.is_commutative()
False
Bases: sage.groups.perm_gps.permgroup_named.PermutationGroup_plg
Helps compute the decomposition of the ramification module
for the Hurwitz curves X (over CC say) with automorphism group
G = PSL(2,q), q a “Hurwitz prime” (ie, p is 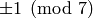 ).
Using this computation and Borne’s formula helps determine the
G-module structure of the RR spaces of equivariant
divisors can be determined explicitly.
).
Using this computation and Borne’s formula helps determine the
G-module structure of the RR spaces of equivariant
divisors can be determined explicitly.
The output is a list of integer multiplicities: [m1,...,mn], where n is the number of conj classes of G=PSL(2,p) and mi is the multiplicity of pi_i in the ramification module of a Hurwitz curve with automorphism group G. Here IrrRepns(G) = [pi_1,...,pi_n] (in the order listed in the output of self.character_table()).
This means, for example, that the trivial representation does not occur in the ramification module of a Hurwitz curve with automorphism group PSL(2,13), since the trivial representation is listed first and that entry has multiplicity 0. The “randomness” is due to the fact that GAP randomly orders the conjugacy classes of the same order in the list of all conjugacy classes. Similarly, there is some randomness to the ordering of the characters.
If you try to use this function on a group PSL(2,q) where q is not a (smallish) “Hurwitz prime”, an error message will be printed.
Helps compute the decomposition of the ramification module for the modular curve X(p) (over CC say) with automorphism group G = PSL(2,q), q a prime > 5. Using this computation and Borne’s formula helps determine the G-module structure of the RR spaces of equivariant divisors can be determined explicitly.
The output is a list of integer multiplicities: [m1,...,mn], where n is the number of conj classes of G=PSL(2,p) and mi is the multiplicity of pi_i in the ramification module of a modular curve with automorphism group G. Here IrrRepns(G) = [pi_1,...,pi_n] (in the order listed in the output of self.character_table()).
This means, for example, that the trivial representation does not occur in the ramification module of X(7), since the trivial representation is listed first and that entry has multiplicity 0. The “randomness” is due to the fact that GAP randomly orders the conjugacy classes of the same order in the list of all conjugacy classes. Similarly, there is some randomness to the ordering of the characters.
Bases: sage.groups.perm_gps.permgroup_named.PermutationGroup_unique
sage: G = PGL(2,3) sage: G.base_ring() Finite Field of size 3
sage: G = PSL(2,3) sage: G.base_ring() Finite Field of size 3
Bases: sage.groups.perm_gps.permgroup_named.PermutationGroup_plg
Bases: sage.groups.perm_gps.permgroup_named.PermutationGroup_unique
This is a class used to factor out some of the commonality in the SymmetricGroup and AlternatingGroup classes.
Returns the list of positive integers on which this group acts.
Bases: sage.groups.perm_gps.permgroup_named.DiCyclicGroup
The quaternion group of order 8.
EXAMPLES:
The quaternion group is one of two non-abelian groups of order 8,
the other being the dihedral group 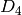 . One way to describe this
group is with three generators,
. One way to describe this
group is with three generators, 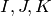 , so the whole group is
then given as the set
, so the whole group is
then given as the set 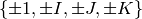 with relations
such as
with relations
such as 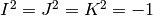 ,
, 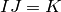 and
and  .
.
The examples below illustrate how to use this group in a similar manner, by testing some of these relations. The representation used here is the left-regular representation.
sage: Q = QuaternionGroup()
sage: I = Q.gen(0)
sage: J = Q.gen(1)
sage: K = I*J
sage: [I,J,K]
[(1,2,3,4)(5,6,7,8), (1,5,3,7)(2,8,4,6), (1,8,3,6)(2,7,4,5)]
sage: neg_one = I^2; neg_one
(1,3)(2,4)(5,7)(6,8)
sage: J^2 == neg_one and K^2 == neg_one
True
sage: J*I == neg_one*K
True
sage: Q.center().order() == 2
True
sage: neg_one in Q.center()
True
Bases: sage.groups.perm_gps.permgroup_named.PermutationGroup_unique
Bases: sage.groups.perm_gps.permgroup_named.PermutationGroup_symalt
Indexing sets of descent of the symmetric group.
EXAMPLES:
sage: S8 = SymmetricGroup(8)
sage: S8.index_set()
(1, 2, 3, 4, 5, 6, 7)
sage: S = SymmetricGroup([3,1,4,5])
sage: S.index_set()
(3, 1, 4)
For  in the index set of self, this returns the
elementary transposition
in the index set of self, this returns the
elementary transposition 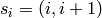 .
.
EXAMPLES:
sage: A = SymmetricGroup(5)
sage: A.simple_reflection(3)
(3,4)
sage: A = SymmetricGroup([2,3,7])
sage: A.simple_reflections()
Finite family {2: (2,3), 3: (3,7)}
INPUT:
- d – an integer (optional)
Returns the set of all transitive groups of a given degree d. If d is not specified, it returns the set of all transitive groups.
Warning: TransitiveGroups requires the optional GAP database package. Please install it with sage -i database_gap.
EXAMPLES:
sage: TransitiveGroups(3)
Transitive Groups of degree 3
sage: TransitiveGroups(7)
Transitive Groups of degree 7
sage: TransitiveGroups(8)
Transitive Groups of degree 8
sage: TransitiveGroups()
Transitive Groups
Warning
in practice, the database currently only contains transitive groups up to degree 30:
sage: TransitiveGroups(31).cardinality() # requires optional database_gap
...
NotImplementedError: Only the transitive groups of order less than 30 are available in GAP's database
Bases: sage.sets.disjoint_union_enumerated_sets.DisjointUnionEnumeratedSets
The infinite set of all transitive groups.
EXAMPLES:
sage: L = TransitiveGroups(); L
Transitive Groups
sage: L.category()
Category of infinite enumerated sets
sage: L.cardinality()
+Infinity
sage: p = L.__iter__() # requires optional database_gap
sage: (p.next(), p.next(), p.next(), p.next(), p.next(), p.next(), p.next(), p.next()) # requires optional database_gap
(Transitive group number 1 of degree 0, Transitive group number 1 of degree 1, Transitive group number 1 of degree 2, Transitive group number 1 of degree 3, Transitive group number 2 of degree 3, Transitive group number 1 of degree 4, Transitive group number 2 of degree 4, Transitive group number 3 of degree 4)
TESTS:
sage: TestSuite(TransitiveGroups()).run() # requires optional database_gap # long time
Bases: sage.structure.unique_representation.UniqueRepresentation, sage.structure.parent.Parent
The set of all transitive groups of a given (small) degree.
EXAMPLES:
sage: S = TransitiveGroups(4); S # requires optional database_gap
Transitive Groups of degree 4
sage: list(S) # requires optional database_gap
[Transitive group number 1 of degree 4, Transitive group number 2 of degree 4, Transitive group number 3 of degree 4, Transitive group number 4 of degree 4, Transitive group number 5 of degree 4]
sage: TransitiveGroups(5).an_element() # requires optional database_gap
Transitive group number 1 of degree 5
We write the cardinality of all transitive groups of degree 5:
sage: for G in TransitiveGroups(5): # requires optional database_gap
... print G.cardinality()
5
10
20
60
120
TESTS:
sage: TestSuite(TransitiveGroups(3)).run() # requires optional database_gap
Returns the cardinality of self, that is the number of transitive groups of a given degree.
EXAMPLES:
sage: TransitiveGroups(0).cardinality() # requires optional database_gap
1
sage: TransitiveGroups(2).cardinality() # requires optional database_gap
1
sage: TransitiveGroups(7).cardinality() # requires optional database_gap
7
sage: TransitiveGroups(12).cardinality() # requires optional database_gap
301
sage: [TransitiveGroups(i).cardinality() for i in range(11)] # requires optional database_gap
[1, 1, 1, 2, 5, 5, 16, 7, 50, 34, 45]
Warning
The database_gap contains all transitive groups up to degree 30:
sage: TransitiveGroups(31).cardinality() # requires optional database_gap
...
NotImplementedError: Only the transitive groups of order less than 30 are available in GAP's database
TESTS:
sage: type(TransitiveGroups(12).cardinality()) # requires optional database_gap
<type 'sage.rings.integer.Integer'>
sage: type(TransitiveGroups(0).cardinality())
<type 'sage.rings.integer.Integer'>