Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Category Theory »

AUTHORS:
Every Sage object lies in a category. Categories in Sage are modeled on the mathematical idea of category, and are distinct from Python classes, which are a programming construct.
In most cases, typing x.category() returns the
category to which 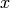 belongs. If
belongs. If  is a category
and
is a category
and 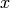 is any object,
is any object, 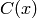 tries to make an
object in
tries to make an
object in  from
from 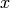 .
.
See Category and sage.categories.primer for more details.
EXAMPLES:
We create a couple of categories:
sage: Sets()
Category of sets
sage: GSets(AbelianGroup([2,4,9]))
Category of G-sets for Multiplicative Abelian Group isomorphic to C2 x C4 x C9
sage: Semigroups()
Category of semigroups
sage: VectorSpaces(FiniteField(11))
Category of vector spaces over Finite Field of size 11
sage: Ideals(IntegerRing())
Category of ring ideals in Integer Ring
The default category for elements 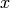 of an object
of an object 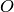 is the category
of all objects of
is the category
of all objects of 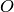 . For example:
. For example:
sage: V = VectorSpace(RationalField(), 3)
sage: x = V.gen(1)
sage: x.category()
Category of elements of Vector space of dimension 3 over Rational Field
Bases: sage.categories.category.Category
An abstract base class for all categories of abstract parents
See Category.abstract_category.
Caveat: specifications subject to change shortly.
The super categories of self that are not derived from the inheritance diagram of the base category, as a list.
EXAMPLES:
sage: C = GradedHopfAlgebrasWithBasis(QQ).abstract_category()
sage: C.extra_super_categories()
[Category of graded hopf algebras with basis over Rational Field]
Returns the immediate super categories, as per Category.super_categories().
EXAMPLES:
sage: C = GradedHopfAlgebrasWithBasis(QQ).abstract_category()
sage: C.super_categories()
[Category of graded hopf algebras over Rational Field]
Bases: sage.structure.unique_representation.UniqueRepresentation, sage.structure.sage_object.SageObject
The base class for modeling mathematical categories, like for example:
See sage.categories.primer for an introduction to categories in Sage, their relevance, purpose and usage. The documentation below focus on their implementation.
Technically, a category is an instance of the class Category or some of its subclasses. Some categories, like VectorSpaces, are parametrized: VectorSpaces(QQ) is one of many instances of the class VectorSpaces. On the other hand, EuclideanRings() is the single instance of the class EuclideanRings.
Recall that an algebraic structure (say the ring QQ[x]) is modelled in Sage by an object which is called a parent. This object belongs to certain categories (here EuclideanRings() and Algebras()). The elements of the ring are themselves objects.
The class of a category (say EuclideanRings) can define simultaneously:
This is achieved as follows:
sage: from sage.categories.all import Category
sage: class EuclideanRings(Category):
... # operations on the category itself
... def super_categories(self):
... [Rings()]
...
... def dummy(self): # TODO: find some good examples
... pass
...
... class ParentMethods: # holds the generic operations on parents
... # find a good example of operation
... pass
...
... class ElementMethods:# holds the generic operations on elements
... def gcd(x,y):
... # Euclid algorithms
... pass
Note that the EuclideanRings.ParentMethods and .Element class above do not inherit from anything. They are merely containers of operations. The hierarchy between the different categories is defined once at the level of the categories. Behind the scene, a parallel hierarchy of classes is built automatically from all the .ParentMethods classes. Then, a parent in a category receives the appropriate operations from all the super categories by usual class inheritance. Similarly, a third hierarchy of classes is built for elements from the .Elements.
EXAMPLES:
We define a hierarchy of four categories As(), Bs(), Cs(), Ds() with a diamond inheritance. Think for example:
As(): the category of sets
Bs(): the category of additive groups
Cs(): the category of multiplicative monoids
Ds(): the category of rings
sage: from sage.categories.all import Category sage: from sage.misc.lazy_attribute import lazy_attribute sage: class As (Category): ... @cached_method ... def super_categories(self): ... return [] ... ... class ParentMethods: ... def fA(self): ... return “A” ... f = fA ... sage: class Bs (Category): ... @cached_method ... def super_categories(self): ... return [As()] ... ... class ParentMethods: ... def fB(self): ... return “B” ... sage: class Cs (Category): ... @cached_method ... def super_categories(self): ... return [As()] ... ... class ParentMethods: ... def fC(self): ... return “C” ... f = fC ... sage: class Ds (Category): ... @cached_method ... def super_categories(self): ... return [Bs(),Cs()] ... ... class ParentMethods: ... def fD(self): ... return “D” ...
Categories should always have uniq representation. We check this before proceeding:
sage: id(As()) == id(As()) True sage: As().parent_class == As().parent_class True
We construct a parent in the category Ds() (that is an instance of Ds().parent_class, and check that it has access to all the methods provided by all the categories, with the appropriate inheritance order.
sage: D = Ds().parent_class() sage: [ D.fA(), D.fB(), D.fC(), D.fD() ] [‘A’, ‘B’, ‘C’, ‘D’] sage: D.f() ‘C’
sage: C = Cs().parent_class() sage: [ C.fA(), C.fC() ] [‘A’, ‘C’] sage: C.f() ‘C’
Here is the parallel hierarchy of classes which has been built automatically, together with the method resolution order (.mro()):
sage: As().parent_class
<class '__main__.As.parent_class'>
sage: As().parent_class.__bases__
(<type 'object'>,)
sage: As().parent_class.mro()
[<class '__main__.As.parent_class'>, <type 'object'>]
sage: Bs().parent_class
<class '__main__.Bs.parent_class'>
sage: Bs().parent_class.__bases__
(<class '__main__.As.parent_class'>,)
sage: Bs().parent_class.mro()
[<class '__main__.Bs.parent_class'>, <class '__main__.As.parent_class'>, <type 'object'>]
sage: Cs().parent_class
<class '__main__.Cs.parent_class'>
sage: Cs().parent_class.__bases__
(<class '__main__.As.parent_class'>,)
sage: Cs().parent_class.__mro__
(<class '__main__.Cs.parent_class'>, <class '__main__.As.parent_class'>, <type 'object'>)
sage: Ds().parent_class
<class '__main__.Ds.parent_class'>
sage: Ds().parent_class.__bases__
(<class '__main__.Bs.parent_class'>, <class '__main__.Cs.parent_class'>)
sage: Ds().parent_class.mro()
[<class '__main__.Ds.parent_class'>, <class '__main__.Bs.parent_class'>, <class '__main__.Cs.parent_class'>, <class '__main__.As.parent_class'>, <type 'object'>]
Note that that two categories in the same class need not have the same super_categories. For example, Algebras(QQ) has VectorSpaces(QQ) as super category, whereas Algebras(ZZ) only has Modules(ZZ) as super category. In particular, the constructed parent_class and element_class will differ (inheriting, or not, methods specific for vector spaces). On the other hand, caching ensures that two identical hierarchy of classes are built only once:
# TODO: redo the same with Algebras
# and show the mro for Algebras(QQ) w.r.t Algebras(ZZ)
# 2009/03/11: this feature is temporarily broken, due to the current work around for pickling
sage: Coalgebras(QQ).parent_class is Coalgebras(FractionField(QQ[x])).parent_class # todo: not implemented
True
We now construct a parent in the usual way:
sage: class myparent(Parent): ... def __init__(self): ... Parent.__init__(self, category=Ds()) ... def g(self): ... return “myparent” ... class Element: ... pass sage: D = myparent() sage: D.__class__ <class ‘__main__.myparent_with_category’> sage: D.__class__.__bases__ (<class ‘__main__.myparent’>, <class ‘__main__.Ds.parent_class’>) sage: D.__class__.mro() [<class ‘__main__.myparent_with_category’>, <class ‘__main__.myparent’>, <type ‘sage.structure.parent.Parent’>, <type ‘sage.structure.category_object.CategoryObject’>, <type ‘sage.structure.sage_object.SageObject’>, <class ‘__main__.Ds.parent_class’>, <class ‘__main__.Bs.parent_class’>, <class ‘__main__.Cs.parent_class’>, <class ‘__main__.As.parent_class’>, <type ‘object’>] sage: D.fA() ‘A’ sage: D.fB() ‘B’ sage: D.fC() ‘C’ sage: D.fD() ‘D’ sage: D.f() ‘C’ sage: D.g() ‘myparent’
sage: D.element_class <class ‘__main__.myparent_with_category.element_class’> sage: D.element_class.mro() [<class ‘__main__.myparent_with_category.element_class’>, <class __main__.Element at ...>, <class ‘sage.categories.category.Ds.element_class’>, <class ‘sage.categories.category.Bs.element_class’>, <class ‘sage.categories.category.Cs.element_class’>, <class ‘sage.categories.category.As.element_class’>, <type ‘object’>]
TESTS:
sage: import __main__
sage: __main__.myparent = myparent
sage: __main__.As = As
sage: __main__.Bs = Bs
sage: __main__.Cs = Cs
sage: __main__.Ds = Ds
sage: loads(dumps(Ds)) is Ds
True
sage: loads(dumps(Ds())) is Ds()
True
sage: loads(dumps(Ds().element_class)) is Ds().element_class
True
INPUT:
- self – a subcategory of Sets()
- base_ring – a ring
Returns the category of objects constructed as algebras of objects of self over base_ring.
EXAMPLES:
sage: Monoids().Algebras(QQ)
Category of monoid algebras over Rational Field
sage: Groups().Algebras(QQ) # todo: update once there will be a category for group algebras
Category of monoid algebras over Rational Field
sage: M = Monoids().example(); M
An example of a monoid: the free monoid generated by ('a', 'b', 'c', 'd')
sage: A = M.algebra(QQ); A
Free module generated by An example of a monoid: the free monoid generated by ('a', 'b', 'c', 'd') over Rational Field
sage: A.category()
Category of monoid algebras over Rational Field
INPUT:
- self – a concrete category
Returns the category of parents constructed as cartesian products of parents in self.
See CartesianProductFunctor for more information
EXAMPLES:
sage: Sets().CartesianProducts()
Category of Cartesian products of sets
sage: Semigroups().CartesianProducts()
Category of Cartesian products of semigroups
sage: EuclideanDomains().CartesianProducts()
Category of Cartesian products of monoids
Returns the category of duals of objects of self.
INPUT:
- self – a subcategory of vector spaces over some base ring
The dual of a vector space 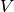 is the space consisting of all
linear functionals on
is the space consisting of all
linear functionals on 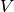 (http://en.wikipedia.org/wiki/Dual_space).
Additional structure on
(http://en.wikipedia.org/wiki/Dual_space).
Additional structure on 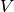 can endow its dual with additional
structure; e.g. if
can endow its dual with additional
structure; e.g. if 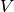 is an algebra, then its dual is a
coalgebra.
is an algebra, then its dual is a
coalgebra.
This returns the category of dual of spaces in self endowed with the appropriate additional structure.
See also CovariantFunctorialConstruction.
TODO: add support for graded duals.
EXAMPLES:
sage: VectorSpaces(QQ).DualObjects()
Category of duals of vector spaces over Rational Field
The dual of a vector space is a vector space:
sage: VectorSpaces(QQ).DualObjects().super_categories()
[Category of vector spaces over Rational Field]
The dual of an algebra space is a coalgebra:
sage: Algebras(QQ).DualObjects().super_categories()
[Category of coalgebras over Rational Field, Category of duals of vector spaces over Rational Field]
The dual of a coalgebra space is an algebra:
sage: Coalgebras(QQ).DualObjects().super_categories()
[Category of algebras over Rational Field, Category of duals of vector spaces over Rational Field]
As a shorthand, this category can be accessed with the dual() method:
sage: VectorSpaces(QQ).dual()
Category of duals of vector spaces over Rational Field
TESTS:
sage: C = VectorSpaces(QQ).DualObjects()
sage: C.base_category()
Category of vector spaces over Rational Field
sage: C.super_categories()
[Category of vector spaces over Rational Field]
sage: latex(C)
\mathbf{DualObjects}(\mathbf{VectorSpaces}_{\Bold{Q}})
sage: TestSuite(C).run()
Given a concrete category As() (i.e. a subcategory of Sets()), As().IsomorphicObjects() returns the category of objects of As() endowed with a distinguished description as the image of some other object of As() by an isomorphism.
See Subquotients() for background.
EXAMPLES:
sage: C = Sets().IsomorphicObjects(); C
Category of isomorphic objects of sets
sage: C.super_categories()
[Category of subobjects of sets, Category of quotients of sets]
sage: C.all_super_categories()
[Category of isomorphic objects of sets,
Category of subobjects of sets,
Category of quotients of sets,
Category of subquotients of sets,
Category of sets,
Category of sets with partial maps,
Category of objects]
Unless something specific about isomorphic objects is implemented for this category, one actually get an optimized super category:
sage: C = Semigroups().IsomorphicObjects(); C
Join of Category of quotients of semigroups and Category of isomorphic objects of sets
TESTS:
sage: TestSuite(Sets().IsomorphicObjects()).run()
Given a concrete category As() (i.e. a subcategory of Sets()), As().Quotients() returns the category of objects of As() endowed with a distinguished description as quotient of some other object of As().
See Subquotients() for background.
EXAMPLES:
sage: C = Semigroups().Quotients(); C
Category of quotients of semigroups
sage: C.super_categories()
[Category of subquotients of semigroups, Category of quotients of sets]
sage: C.all_super_categories()
[Category of quotients of semigroups, Category of subquotients of semigroups, Category of semigroups,
Category of subquotients of magmas, Category of magmas,
Category of quotients of sets, Category of subquotients of sets, Category of sets,
Category of sets with partial maps,
Category of objects]
The caller is responsible for checking that the given category admits a well defined category of quotients:
sage: EuclideanDomains().Quotients()
Join of Category of euclidean domains and Category of subquotients of monoids and Category of quotients of semigroups
TESTS:
sage: TestSuite(C).run()
Given a concrete category As() (i.e. a subcategory of Sets()), As().Subobjects() returns the category of objects of As() endowed with a distinguished description as subobject of some other object of As().
See Subquotients() for background.
EXAMPLES:
sage: C = Sets().Subobjects(); C
Category of subobjects of sets
sage: C.super_categories()
[Category of subquotients of sets]
sage: C.all_super_categories()
[Category of subobjects of sets,
Category of subquotients of sets,
Category of sets,
Category of sets with partial maps,
Category of objects]
Unless something specific about subobjects is implemented for this category, one actually get an optimized super category:
sage: C = Semigroups().Subobjects(); C
Join of Category of subquotients of semigroups and Category of subobjects of sets
The caller is responsible for checking that the given category admits a well defined category of subobjects.
TESTS:
sage: Semigroups().Subobjects().is_subcategory(Semigroups().Subquotients())
True
sage: TestSuite(C).run()
Given a concrete category self == As() (i.e. a subcategory of Sets()), As().Subquotients() returns the category of objects of As() endowed with a distinguished description as subquotient of some other object of As().
EXAMPLES:
sage: Monoids().Subquotients()
Category of subquotients of monoids
A parent 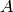 in As() is further in As().Subquotients() if
there is a distinguished parent
in As() is further in As().Subquotients() if
there is a distinguished parent 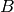 in As(), called the
ambient space, a subspace
in As(), called the
ambient space, a subspace 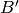 of
of 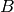 and a pair of structure
preserving maps:
and a pair of structure
preserving maps:
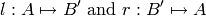
called respectively the lifting map and retract map such that
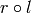 is the identity of
is the identity of 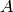 . What exactly structure
preserving means is explicited in each category; this typically
states that, for each operation
. What exactly structure
preserving means is explicited in each category; this typically
states that, for each operation 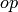 of the category, there is a
commutative diagram such that:
of the category, there is a
commutative diagram such that:
for all, one has
This allows for deriving the operations on 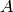 from those on
from those on 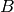 .
.
Note: this is a slightly weaker definition than that found on http://en.wikipedia.org/wiki/Subquotient: B’ is not necessarily required to be a subobject of B.
Assumptions:
For any category As(), As().Subquotients() is a subcategory of As().
Example: a subquotient of a group is a group (e.g. a left or right quotients of a group by a non normal subgroup is not in this category).
This construction is covariant: if As() is a subcategory of Bs(), then As().Subquotients() is a subcategory of Bs().Subquotients()
Example: if 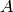 is a distinguished subquotient of
is a distinguished subquotient of 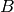 in the category of
groups, then is is also a subquotient of
in the category of
groups, then is is also a subquotient of 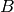 in the category of monoids.
in the category of monoids.
If the user (or a program) calls As().Subquotients(), then it is
assumed that subquotients are well defined in this category. This is not
checked, and probably never will. Note that, if a category 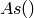 does
not specify anything about its subquotients, then it’s subquotient
category looks like this:
does
not specify anything about its subquotients, then it’s subquotient
category looks like this:
sage: EuclideanDomains().Subquotients()
Join of Category of euclidean domains and Category of subquotients of monoids
Interface: the ambient space of 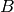 is given by B.ambient(). The
lifting and retract map are implemented respectively as methods
B.lift(b) and B.retract(a). As a shorthand, one can use
alternatively b.lift():
is given by B.ambient(). The
lifting and retract map are implemented respectively as methods
B.lift(b) and B.retract(a). As a shorthand, one can use
alternatively b.lift():
sage: S = Semigroups().Subquotients().example(); S
An example of a (sub)quotient semigroup: a quotient of the left zero semigroup
sage: S.ambient()
An example of a semigroup: the left zero semigroup
sage: S(3).lift().parent()
An example of a semigroup: the left zero semigroup
sage: S(3) * S(1) == S.retract( S(3).lift() * S(1).lift() )
True
See S? for more.
TODO: use a more interesting example, like 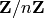 .
.
The two most common use cases are:
- quotients, when
and
is a morphism; then
is a canonical quotient map from
to
)
- subobjects (when
is an embedding from
into
).
See respectively Quotients and Subobjects.
TESTS:
sage: TestSuite(Sets().Subquotients()).run()
INPUT:
- self – a subcategory of ModulesWithBasis(...)
Returns the category of objects constructed as tensor products of objects of self.
See TensorProductFunctor for more information
EXAMPLES:
sage: ModulesWithBasis(QQ).TensorProducts()
Category of tensor products of modules with basis over Rational Field
An abstract parent is a parent which models an abstract algebraic structure which has several concrete representations.
This returns a mostly technical category which provides support tools for handling the different representation, and in particular the coercions between them.
It can be manually specified by defining a class AbstractCategory as a member of this category.
Typically, FiniteDimensionalModulesWithBasis(QQ).abstract_category()
will be in charge, whenever a coercion 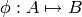 is
registered, to register
is
registered, to register 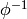 as coercion
as coercion 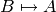 if there is none defined yet.
if there is none defined yet.
This is the analog of the 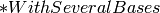 categories in MuPAD-Combinat.
categories in MuPAD-Combinat.
TODO: find a better name!
The hierarchy of all abstract categories is built in parallel to that of their base categories, optimizing away those categories which do not have an AbstractCategory.
Design question: currently self.abstract_category() is a subcategory of self by default. Is this desirable? For example, Algebras(QQ).abstract_category() should definitely be a subcategory of Algebras(QQ). On the other hand, AlgebrasWithBasis(QQ).abstract_category() should be a subcategory of Algebras(QQ), but not of AlgebrasWithBasis(QQ). This is because AlgebrasWithBasis(QQ) is specifying something about the concrete representation.
EXAMPLES:
sage: Semigroups().abstract_category()
Category of semigroups
sage: C = GradedHopfAlgebrasWithBasis(QQ).abstract_category(); C
Category of abstract graded hopf algebras with basis over Rational Field
sage: C.all_super_categories()
[Category of abstract graded hopf algebras with basis over Rational Field,
Category of graded hopf algebras over Rational Field,
Category of graded bialgebras over Rational Field,
Category of graded algebras over Rational Field,
Category of graded coalgebras over Rational Field,
Category of graded modules over Rational Field,
Category of hopf algebras over Rational Field,
Category of bialgebras over Rational Field,
Category of algebras over Rational Field,
...]
Returns a linear extension (topological sort) of all the (proper) super categories of this category, and cache the result.
INPUT:
- proper: a boolean; defaults to False. Whether to exclude this category.
FIXME:
EXAMPLES:
sage: C = GradedHopfAlgebrasWithBasis(QQ).abstract_category(); C
Category of abstract graded hopf algebras with basis over Rational Field
sage: C.all_super_categories()
[Category of abstract graded hopf algebras with basis over Rational Field,
Category of graded hopf algebras over Rational Field,
Category of graded bialgebras over Rational Field,
Category of graded algebras over Rational Field,
Category of graded coalgebras over Rational Field,
Category of graded modules over Rational Field,
Category of hopf algebras over Rational Field,
Category of bialgebras over Rational Field,
Category of algebras over Rational Field,
...]
Returns an instance of this class
EXAMPLES:
sage: Rings.an_instance()
Category of rings
Parametrized categories should overload this default implementation to provide appropriate arguments:
sage: Algebras.an_instance() Category of algebras over Rational Field sage: Bimodules.an_instance() Category of bimodules over Rational Field on the left and Real Field with 53 bits of precision on the right sage: AlgebraIdeals.an_instance() Category of algebra ideals in Univariate Polynomial Ring in x over Rational Field
Returns the category of this category. So far all categories are in the category of objects.
EXAMPLES:
sage: Sets().category()
Category of objects
sage: VectorSpaces(QQ).category()
Category of objects
Returns the graph of all super categories of this category
EXAMPLES:
sage: C = Algebras(QQ)
sage: G = C.category_graph()
sage: G.is_directed_acyclic()
True
sage: G.girth()
4
Returns the category of duals of objects of self.
INPUT:
- self – a subcategory of vector spaces over some base ring
The dual of a vector space 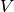 is the space consisting of all
linear functionals on
is the space consisting of all
linear functionals on 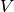 (http://en.wikipedia.org/wiki/Dual_space).
Additional structure on
(http://en.wikipedia.org/wiki/Dual_space).
Additional structure on 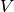 can endow its dual with additional
structure; e.g. if
can endow its dual with additional
structure; e.g. if 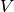 is an algebra, then its dual is a
coalgebra.
is an algebra, then its dual is a
coalgebra.
This returns the category of dual of spaces in self endowed with the appropriate additional structure.
See also CovariantFunctorialConstruction.
TODO: add support for graded duals.
EXAMPLES:
sage: VectorSpaces(QQ).DualObjects()
Category of duals of vector spaces over Rational Field
The dual of a vector space is a vector space:
sage: VectorSpaces(QQ).DualObjects().super_categories()
[Category of vector spaces over Rational Field]
The dual of an algebra space is a coalgebra:
sage: Algebras(QQ).DualObjects().super_categories()
[Category of coalgebras over Rational Field, Category of duals of vector spaces over Rational Field]
The dual of a coalgebra space is an algebra:
sage: Coalgebras(QQ).DualObjects().super_categories()
[Category of algebras over Rational Field, Category of duals of vector spaces over Rational Field]
As a shorthand, this category can be accessed with the dual() method:
sage: VectorSpaces(QQ).dual()
Category of duals of vector spaces over Rational Field
TESTS:
sage: C = VectorSpaces(QQ).DualObjects()
sage: C.base_category()
Category of vector spaces over Rational Field
sage: C.super_categories()
[Category of vector spaces over Rational Field]
sage: latex(C)
\mathbf{DualObjects}(\mathbf{VectorSpaces}_{\Bold{Q}})
sage: TestSuite(C).run()
A common super class for all elements of parents in this category.
EXAMPLES:
sage: C = Algebras(QQ).element_class; C
<class 'sage.categories.algebras.Algebras.element_class'>
sage: type(C)
<class 'sage.structure.dynamic_class.DynamicMetaclass'>
Returns an object in this category. Most of the time, this is a parent.
For all those applications, the implementation of the object shall be kept to a strict minimum. The object is therefore not meant to be used for other applications; most of the time a full featured version is available elsewhere in Sage, and should be used insted.
Technical note: by default FooBar(...).example() is constructed by looking up sage.categories.examples.foo_bar.Example and calling it as Example(category = FooBar). Extra positional or named parameters are also passed down. Categories are welcome to override this.
EXAMPLES:
sage: Semigroups().example()
An example of a semigroup: the left zero semigroup
sage: Monoids().Subquotients().example()
NotImplemented
Returns the category for homsets between objects this category.
A category which needs to give specific information about this category should provide a HomCategory class.
To avoid generating billions of categories, if there is nothing specific for homsets of this category, then this just returns the join of the categories of homsets of the super categories.
EXAMPLES:
sage: Sets().hom_category()
Category of hom sets in Category of sets
Returns whether this category is abelian.
An abelian category is a category satisfying:
Equivalently, one can define an increasing sequence of conditions:
EXAMPLES:
sage: Modules(ZZ).is_abelian()
True
sage: FreeModules(ZZ).is_abelian()
False
sage: FreeModules(QQ).is_abelian()
True
sage: CommutativeAdditiveGroups().is_abelian()
True
sage: Semigroups().is_abelian()
Traceback (most recent call last):
NotImplementedError: is_abelian
Returns True if self is naturally embedded as a subcategory of c.
EXAMPLES:
sage: AbGrps = CommutativeAdditiveGroups()
sage: Rings().is_subcategory(AbGrps)
True
sage: AbGrps.is_subcategory(Rings())
False
The is_subcategory function takes into account the base.
sage: M3 = VectorSpaces(FiniteField(3))
sage: M9 = VectorSpaces(FiniteField(9, 'a'))
sage: M3.is_subcategory(M9)
False
Join categories are properly handled:
sage: CatJ = Category.join((CommutativeAdditiveGroups(), Semigroups()))
sage: Rings().is_subcategory(CatJ)
True
sage: V3 = VectorSpaces(FiniteField(3))
sage: POSet = PartiallyOrderedSets()
sage: PoV3 = Category.join((V3, POSet))
sage: A3 = AlgebrasWithBasis(FiniteField(3))
sage: PoA3 = Category.join((A3, POSet))
sage: PoA3.is_subcategory(PoV3)
True
sage: PoV3.is_subcategory(PoV3)
True
sage: PoV3.is_subcategory(PoA3)
False
Returns the join of the input categories in the lattice of categories
INPUT:
- a sequence of categories (FIXME: should this be a list or iterable?)
- as_list: a boolean, False by default (keyword only)
EXAMPLES:
sage: J = Category.join((Groups(), CommutativeAdditiveMonoids())); J
Join of Category of groups and Category of commutative additive monoids
sage: J.super_categories()
[Category of groups, Category of commutative additive monoids]
sage: J.all_super_categories(proper = True)
[Category of groups,
Category of monoids,
Category of semigroups,
Category of magmas,
Category of commutative additive monoids,
Category of commutative additive semigroups,
Category of additive magmas,
Category of sets,
Category of sets with partial maps,
Category of objects]
This is an associative operation:
sage: Category.join((Objects(), Sets(), Category.join((Monoids(), Sets(), Monoids())), Category.join((Objects(), CommutativeAdditiveGroups()))))
Join of Category of monoids and Category of commutative additive groups
The join of a single category is the category itself:
sage: Category.join((Monoids(),))
Category of monoids
Similarly, the join of several mutually comparable categories is the smallest one:
sage: Category.join((Sets(), Rings(), Monoids()))
Category of rings
If the optional parameter as_list is True, this just returns the super categories of the join as a list, without constructing the join category itself:
sage: Category.join((Groups(), CommutativeAdditiveMonoids()), as_list=True)
[Category of groups, Category of commutative additive monoids]
sage: Category.join((Sets(), Rings(), Monoids()), as_list=True)
[Category of rings]
Returns the meet of a list of categories
INPUT:
- categories - a non empty list (or iterable) of categories
EXAMPLES:
sage: Category.meet([Algebras(ZZ), Algebras(QQ), Groups()])
Category of monoids
That meet of an empty list should be a category which is a subcategory of all categories, which does not make practical sense:
sage: Category.meet([])
...
ValueError: The meet of an empty list of categories is not implemented
INPUT:
- category - a sub category of self, tuple/list thereof, or None
OUTPUT: a category
Returns category or self if category is None.
EXAMPLES:
sage: Monoids().or_subcategory(Groups())
Category of groups
sage: Monoids().or_subcategory(None)
Category of monoids
If category is a list/tuple, then a join category is returned:
sage: Monoids().or_subcategory((FiniteEnumeratedSets(), Groups()))
Join of Category of finite enumerated sets and Category of groups
An error if raised if category is not a subcategory of self.
sage: Monoids().or_subcategory(EnumeratedSets()) Traceback (most recent call last): ... AssertionError: Subcategory ofrequired; got
A common super class for all parents in this category.
EXAMPLES:
sage: C = Algebras(QQ).parent_class; C
<class 'sage.categories.algebras.Algebras.parent_class'>
sage: type(C)
<class 'sage.structure.dynamic_class.DynamicMetaclass'>
Returns the methods that are required and optional for parents in this category and their elements.
EXAMPLES:
sage: Algebras(QQ).required_methods()
{'parent': {'required': ['__contains__'], 'optional': []}, 'element': {'required': [], 'optional': ['_add_', '_mul_']}}
Bases: sage.categories.category.Category
An abstract base class for all categories of homsets
The hierarchy of homset categories is built in parallel to that of their base categories (which is plain wrong!!!)
The super categories of self that are not derived from the inheritance diagram of the base category, as a list.
EXAMPLES:
sage: HomCategory(Sets()).extra_super_categories()
[]
Returns the immediate super categories, as per Category.super_categories().
EXAMPLES:
sage: HomCategory(Sets()).super_categories()
[Category of hom sets in Category of objects]
Bases: sage.categories.category.Category
A class for joins of several categories. Do not use directly; see Category.join instead.
EXAMPLES:
sage: from sage.categories.category import JoinCategory
sage: J = JoinCategory((Groups(), CommutativeAdditiveMonoids())); J
Join of Category of groups and Category of commutative additive monoids
sage: J.super_categories()
[Category of groups, Category of commutative additive monoids]
sage: J.all_super_categories(proper = True)
[Category of groups, Category of monoids, Category of semigroups, Category of magmas, Category of commutative additive monoids, Category of commutative additive semigroups, Category of additive magmas, Category of sets, Category of sets with partial maps, Category of objects]
Returns the immediate super categories, as per Category.super_categories().
EXAMPLES:
sage: from sage.categories.category import JoinCategory
sage: JoinCategory((Semigroups(), FiniteEnumeratedSets())).super_categories()
[Category of semigroups, Category of finite enumerated sets]
Returns the graph of the categories in Sage
If categories is specified, then the graph will contain the mentionned categories together with all their super categories. Otherwise the graph will contain (an instance of) each category in sage.categories.all (e.g. Algebras(QQ) for algebras).
For readability, the names of the category are shortened, and in particular do not contain base rings.
EXAMPLES:
sage: G = sage.categories.category.category_graph(categories = [Rings()])
sage: G.vertices()
['additive magmas',
'commutative additive groups',
'commutative additive monoids',
'commutative additive semigroups',
'magmas',
'monoids',
'objects',
'rings',
'rngs',
'semigroups',
'semirings',
'sets',
'sets with partial maps']
sage: G.plot()
sage: sage.categories.category.category_graph().plot()
Returns True if x is a category.
EXAMPLES:
sage: sage.categories.category.is_Category(CommutativeAdditiveSemigroups())
True
sage: sage.categories.category.is_Category(ZZ)
False