Subquotient Functorial Construction

AUTHORS:

• Nicolas M. Thiery (2010): initial revision

sage.categories.subquotients.Subquotients(self)

INPUT:

• self – a concrete category

Given a concrete category self == As() (i.e. a subcategory of Sets()), As().Subquotients() returns the category of objects of As() endowed with a distinguished description as subquotient of some other object of As().

EXAMPLES:

sage: Monoids().Subquotients()
Category of subquotients of monoids

A parent in As() is further in As().Subquotients() if there is a distinguished parent 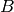in As(), called the ambient space, a subspace 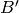of 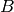and a pair of structure preserving maps:

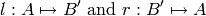
called respectively the lifting map and retract map such that 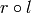is the identity of . What exactly structure preserving means is explicited in each category; this typically states that, for each operation 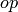of the category, there is a commutative diagram such that:

for all , one has

This allows for deriving the operations on from those on .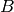

Note: this is a slightly weaker definition than that found on http://en.wikipedia.org/wiki/Subquotient: B’ is not necessarily required to be a subobject of B.

Assumptions:

• For any category As(), As().Subquotients() is a subcategory of As().

  Example: a subquotient of a group is a group (e.g. a left or right quotients of a group by a non normal subgroup is not in this category).

• This construction is covariant: if As() is a subcategory of Bs(), then As().Subquotients() is a subcategory of Bs().Subquotients()

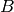  Example: if is a distinguished subquotient of in the category of groups, then is is also a subquotient of 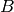in the category of monoids.

• If the user (or a program) calls As().Subquotients(), then it is assumed that subquotients are well defined in this category. This is not checked, and probably never will. Note that, if a category 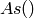does not specify anything about its subquotients, then it’s subquotient category looks like this:

  sage: EuclideanDomains().Subquotients()
  Join of Category of euclidean domains and Category of subquotients of monoids
  

Interface: the ambient space of 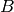is given by B.ambient(). The lifting and retract map are implemented respectively as methods B.lift(b) and B.retract(a). As a shorthand, one can use alternatively b.lift():

sage: S = Semigroups().Subquotients().example(); S
An example of a (sub)quotient semigroup: a quotient of the left zero semigroup
sage: S.ambient()
An example of a semigroup: the left zero semigroup
sage: S(3).lift().parent()
An example of a semigroup: the left zero semigroup
sage: S(3) * S(1) == S.retract( S(3).lift() * S(1).lift() )
True

See S? for more.

TODO: use a more interesting example, like .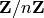

The two most common use cases are:

• quotients, when and is a morphism; then is a canonical quotient map from to )
• subobjects (when is an embedding from into ).

See respectively Quotients and Subobjects.

TESTS:

sage: TestSuite(Sets().Subquotients()).run()

class sage.categories.subquotients.SubquotientsCategory(category, *args)

Bases: sage.categories.covariant_functorial_construction.RegressiveCovariantConstructionCategory