Quotients Functorial Construction

AUTHORS:

• Nicolas M. Thiery (2010): initial revision

sage.categories.quotients.Quotients(self)

INPUT:

• self – a concrete category

Given a concrete category As() (i.e. a subcategory of Sets()), As().Quotients() returns the category of objects of As() endowed with a distinguished description as quotient of some other object of As().

See Subquotients() for background.

EXAMPLES:

sage: C = Semigroups().Quotients(); C
Category of quotients of semigroups
sage: C.super_categories()
[Category of subquotients of semigroups, Category of quotients of sets]
sage: C.all_super_categories()
[Category of quotients of semigroups, Category of subquotients of semigroups, Category of semigroups,
 Category of subquotients of magmas, Category of magmas,
 Category of quotients of sets, Category of subquotients of sets, Category of sets,
 Category of sets with partial maps,
 Category of objects]

The caller is responsible for checking that the given category admits a well defined category of quotients:

sage: EuclideanDomains().Quotients()
Join of Category of euclidean domains and Category of subquotients of monoids and Category of quotients of semigroups

TESTS:

sage: TestSuite(C).run()

class sage.categories.quotients.QuotientsCategory(category, *args)

Bases: sage.categories.covariant_functorial_construction.RegressiveCovariantConstructionCategory

classmethod default_super_categories(category)

Returns the default super categories of category.Quotients()

Mathematical meaning: if 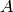is a quotient of 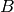in the category , then 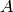is also a subquotient of 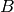in the category .

INPUT:

• cls – the class QuotientsCategory
• category – a category

OUTPUT: a (join) category

In practice, this returns category.Subquotients(), joined together with the result of the method RegressiveCovariantConstructionCategory.default_super_categories() (that is the join of category and cat.Quotients() for each cat in the super categories of category).

EXAMPLES:

Consider category=Groups(), which has cat=Monoids() as super category. Then, a subgroup of a group is simultaneously a subquotient of , a group by itself, and a quotient monoid of G:

sage: Groups().Quotients().super_categories()
[Category of groups, Category of subquotients of monoids, Category of quotients of semigroups]

Mind the last item above: there is indeed currently nothing implemented about quotient monoids.

This resulted from the following call:

sage: sage.categories.quotients.QuotientsCategory.default_super_categories(Groups())
Join of Category of groups and Category of subquotients of monoids and Category of quotients of semigroups