Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Category Theory »

A functorial construction is a collection of functors
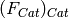 which associate to parents
which associate to parents 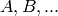 in some
category
in some
category 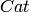 a parent
a parent 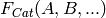 . Examples of functorial
constructions are
. Examples of functorial
constructions are  = cartesian product, tensor product,
= cartesian product, tensor product,
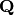 -algebras, ... The category of
-algebras, ... The category of 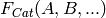 , which only
depends on
, which only
depends on  , is called the (functorial) construction category.
, is called the (functorial) construction category.
A functorial construction is (category)-covariant if for every
categories  and
and 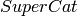 , the category of
, the category of 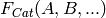 is a subcategory of the category of
is a subcategory of the category of 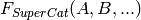 whenever
whenever
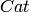 is a subcategory of
is a subcategory of 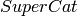 . A functorial construction is
(category)-regressive if the category of
. A functorial construction is
(category)-regressive if the category of 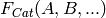 is a
subcategory of
is a
subcategory of 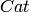 .
.
The goal of this module is to provide generic support for covariant
functorial constructions. In particular, given some parent 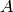 ,
, 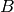 ,
,
 of respective categories
of respective categories 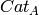 ,
, 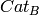 ,
, 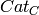 , it provide
tools for calculating the best known category for the parent
, it provide
tools for calculating the best known category for the parent
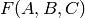 . For examples, knowing that cartesian products of
semigroups (resp. monoids, groups), have a structure of semigroups
(resp. monoids, groups), and given a group
. For examples, knowing that cartesian products of
semigroups (resp. monoids, groups), have a structure of semigroups
(resp. monoids, groups), and given a group 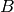 and two monoids
and two monoids 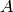 and
and
 it can calculate that
it can calculate that 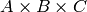 is naturally endowed
with a monoid structure.
is naturally endowed
with a monoid structure.
See CovariantFunctorialConstruction, CovariantConstructionCategory and RegressiveCovariantConstructionCategory for more details.
AUTHORS:
- Nicolas M. Thiery (2010): initial revision
Bases: sage.categories.category.Category
Abstract class for categories 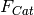 obtained through a
covariant functorial construction
obtained through a
covariant functorial construction
Returns the base category of the category self
For any category B = 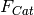 obtained through a functorial
construction
obtained through a functorial
construction  , the call B.base_category() returns the
category
, the call B.base_category() returns the
category 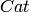
EXAMPLES:
sage: Semigroups().Quotients().base_category()
Category of semigroups
This is the main entry point for constructing the category 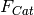 of parents
of parents 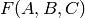 constructed from parents
constructed from parents 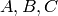 in
in 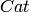 .
.
INPUT:
- cls – the category class for the functorial construction
- category – a category
- *args – further arguments for the functor
OUTPUT: the image category of the functor 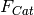
EXAMPLES:
sage: sage.categories.tensor.TensorProductsCategory.category_of(ModulesWithBasis(QQ))
Category of tensor products of modules with basis over Rational Field
sage: sage.categories.algebra_functor.AlgebrasCategory.category_of(FiniteMonoids(), QQ)
Category of monoid algebras over Rational Field
Returns the default super categories of 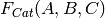 for
for 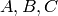 parents in
parents in 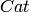 .
.
INPUT:
- cls – the category class for the functor
- category – a category
- *args – further arguments for the functor
OUTPUT: a (join) category
The default implementation is to return the join of the
categories of 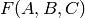 for
for 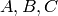 in turn in each of the
super categories of category.
in turn in each of the
super categories of category.
This is implemented as a class method, in order to be able to reconstruct the functorial category associated to each of the super categories of category.
EXAMPLES:
Bialgebras are both algebras and coalgebras:
sage: Bialgebras(QQ).super_categories()
[Category of algebras over Rational Field, Category of coalgebras over Rational Field]
Hence tensor products of bialgebras are tensor products of algebras and tensor products of coalgebras:
sage: Bialgebras(QQ).TensorProducts().super_categories()
[Category of tensor products of algebras over Rational Field, Category of tensor products of coalgebras over Rational Field]
Here is how default_super_categories() was called internally:
sage: sage.categories.tensor.TensorProductsCategory.default_super_categories(Bialgebras(QQ))
Join of Category of tensor products of algebras over Rational Field and Category of tensor products of coalgebras over Rational Field
We now show a similar example, with the Algebra functor
which takes a parameter 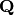 :
:
sage: FiniteMonoids().super_categories()
[Category of finite semigroups, Category of monoids]
sage: FiniteMonoids().Algebras(QQ).super_categories()
[Category of semigroup algebras over Rational Field]
Note that neither the category of finite semigroup algebras nor that of monoid algebras appear in the result; this is because there is currently nothing specific implemented about them.
Here is how default_super_categories() was called internally:
sage: sage.categories.algebra_functor.AlgebrasCategory.default_super_categories(FiniteMonoids(), QQ)
Category of monoid algebras over Rational Field
Returns the extra super categories of a construction category
Default implementation which returns []
EXAMPLES:
sage: Sets().Subquotients().extra_super_categories()
[]
sage: Semigroups().Quotients().extra_super_categories()
[]
Returns the super categories of a construction category
EXAMPLES:
sage: Sets().Subquotients().super_categories()
[Category of sets]
sage: Semigroups().Quotients().super_categories()
[Category of subquotients of semigroups, Category of quotients of sets]
Bases: sage.structure.unique_representation.UniqueRepresentation, sage.structure.sage_object.SageObject
An abstract class for construction functors  (eg
(eg  = cartesian
product, tensor product,
= cartesian
product, tensor product, 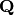 -algebras, ...) such that:
-algebras, ...) such that:
- Each category
(eg
Groups()) can provide a category
for parents constructed via this functor (e.g.
CartesianProductsOf(Groups())).
- For every category
,
is a subcategory of
for every super category
of
(the functorial construction is (category)-covariant).
- For parents
,
,
respectively in the categories
,
,
, the category of
is
where
is the meet of the categories
,
,
.
This covers two slightly different use cases:
In the first use case, one uses directly the construction functor to create new parents:
sage: tensor() # todo: not implemented (add an example)or even new elements, which indirectly constructs the corresponding parent:
sage: tensor(...) # todo: not implementedIn the second use case, one implements a parent, and then put it in the category
to specify supplementary mathematical information about that parent.
The main purpose of this class is to handle automatically the trivial part of the category hiearchy. For example, CartesianProductsOf(Groups()) is set automatically as a subcategory of CartesianProductsOf(Monoids()).
In practice, each subclass of this class should provide the following attributes:
- _functor_category - a string which should match the name of the nested category class to be used in each category to specify information and generic operations for elements of this category.
- _functor_name - an string which specifies the name of the functor, and also (when relevant) of the method on parents and elements used for calling the construction.
TODO: What syntax do we want for 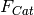 ? For example, for the
tensor product construction, which one of the followings do we want (see
chat on IRC, on 07/12/2009):
? For example, for the
tensor product construction, which one of the followings do we want (see
chat on IRC, on 07/12/2009):
- tensor(Cat)
- tensor((Cat, Cat))
- tensor.of((Cat, Cat))
- tensor.category_from_categories((Cat, Cat, Cat))
- Cat.TensorProducts()
The syntax Cat.TensorProducts() does not supports well multivariate constructions like tensor.of([Algebras(), HopfAlgebras(), ...]). Also it forces every category to be (somehow) aware of all the tensorial construction that could apply to it, even those which are only induced from super categories.
Note: for each functorial construction, there probably is one (or several) largest categories on which it applies. For example, the CartesianProducts() construction makes only sense for concrete categories, that is subcategories of Sets(). Maybe we want to model this one way or the other.
Returns the category of 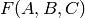 for
for 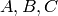 parents in the given categories
parents in the given categories
INPUT:
- self: a functor
- categories: a non empty tuple of categories
EXAMPLES:
sage: Cat1 = Rings()
sage: Cat2 = Groups()
sage: cartesian_product.category_from_categories((Cat1, Cat1, Cat1))
Category of Cartesian products of monoids
sage: cartesian_product.category_from_categories((Cat1, Cat2))
Category of Cartesian products of monoids
Returns the category of 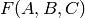 for
for 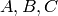 parents in category
parents in category
INPUT:
- self: a functor
- category: a category
EXAMPLES:
sage: tensor.category_from_category(ModulesWithBasis(QQ))
Category of tensor products of modules with basis over Rational Field
# TODO: add support for parametrized functors
Returns the category of 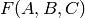 for
for 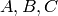 parents.
parents.
INPUT:
- self: a functor F
- parents: a list (or iterable) of parents.
EXAMPLES:
sage: E = CombinatorialFreeModule(QQ, ["a", "b", "c"])
sage: tensor.category_from_parents((E, E, E)) # todo: not implemented (see upcoming category patch #5985)
Bases: sage.categories.covariant_functorial_construction.CovariantConstructionCategory
Abstract class for categories 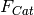 obtained through a
regressive covariant functorial construction
obtained through a
regressive covariant functorial construction
Returns the default super categories of ...
INPUT:
- category – a category
OUTPUT: a join category
This implements the property that an induced subcategory is a subcategory.
EXAMPLES:
A subquotient of a monoid is a monoid, and a subquotient of semigroup:
sage: Monoids().Subquotients().super_categories()
[Category of monoids, Category of subquotients of semigroups]
TESTS:
sage: C = Monoids().Subquotients()
sage: C.__class__.default_super_categories(C.base_category(), *C._args)
Join of Category of monoids and Category of subquotients of semigroups