The most interesting functions to be exported here are matrix_of_frobenius() and adjusted_prec().
Currently this code is limited to the case 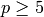 (no
(no
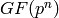 for
for 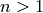 ), and only handles the
elliptic curve case (not more general hyperelliptic curves).
), and only handles the
elliptic curve case (not more general hyperelliptic curves).
REFERENCES:
AUTHORS:
Bases: sage.structure.element.ModuleElement
Represents an element of the form F dx/2y
 where
where 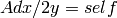 .
. and
and 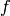 such
that
such
that  where
where  is given in terms of
the
is given in terms of
the  .
.Use homology relations to find  and
and 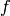 such
that
such
that  where
where  is given in terms of
the
is given in terms of
the  .
.
EXAMPLES:
sage: R.<x> = QQ['x']
sage: E = HyperellipticCurve(x^3-4*x+4)
sage: x, y = E.monsky_washnitzer_gens()
sage: x.diff().reduce_fast()
(x, (0, 0))
sage: y.diff().reduce_fast()
(y*1, (0, 0))
sage: (y^-1).diff().reduce_fast()
((y^-1)*1, (0, 0))
sage: (y^-11).diff().reduce_fast()
((y^-11)*1, (0, 0))
sage: (x*y^2).diff().reduce_fast()
(y^2*x, (0, 0))
Use homology relations to eliminate negative powers of y.
EXAMPLES:
sage: R.<x> = QQ['x']
sage: E = HyperellipticCurve(x^5-3*x+1)
sage: x, y = E.monsky_washnitzer_gens()
sage: (y^-1).diff().reduce_neg_y_fast()
((y^-1)*1, 0 dx/2y)
sage: (y^-5*x^2+y^-1*x).diff().reduce_neg_y_fast()
((y^-1)*x + (y^-5)*x^2, 0 dx/2y)
It leaves non-negative powers of y alone:
sage: y.diff()
((-3)*1 + 5*x^4) dx/2y
sage: y.diff().reduce_neg_y_fast()
(0, ((-3)*1 + 5*x^4) dx/2y)
Use homology relations to eliminate positive powers of y.
EXAMPLES:
sage: R.<x> = QQ['x']
sage: E = HyperellipticCurve(x^3-4*x+4)
sage: x, y = E.monsky_washnitzer_gens()
sage: y.diff().reduce_pos_y_fast()
(y*1, 0 dx/2y)
sage: (y^2).diff().reduce_pos_y_fast()
(y^2*1, 0 dx/2y)
sage: (y^2*x).diff().reduce_pos_y_fast()
(y^2*x, 0 dx/2y)
sage: (y^92*x).diff().reduce_pos_y_fast()
(y^92*x, 0 dx/2y)
sage: w = (y^3 + x).diff()
sage: w += w.parent()(x)
sage: w.reduce_pos_y_fast()
(y^3*1 + x, x dx/2y)
Bases: sage.modules.module.Module
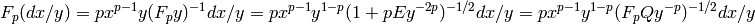
Use Newton’s method to calculate the square root.
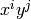 needed to clear all terms with
needed to clear all terms with
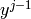 .
.Bases: sage.rings.ring.CommutativeAlgebra
Specialised class for representing the quotient ring
![R[x,T]/(T - x^3 - ax - b)](../../../_images/math/9782d60b9c51301ecc69ce1d04bbd09b29777772.png) , where
, where 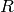 is an
arbitrary commutative base ring (in which 2 and 3 are invertible),
is an
arbitrary commutative base ring (in which 2 and 3 are invertible),
 and
and 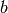 are elements of that ring.
are elements of that ring.
Polynomials are represented internally in the form
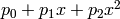 where the
where the 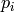 are
polynomials in
are
polynomials in 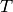 . Multiplication of polynomials always
reduces high powers of
. Multiplication of polynomials always
reduces high powers of  (i.e. beyond
(i.e. beyond 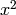 ) to
powers of
) to
powers of 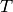 .
.
Hopefully this ring is faster than a general quotient ring because it uses the special structure of this ring to speed multiplication (which is the dominant operation in the frobenius matrix calculation). I haven’t actually tested this theory though...
TODO: - Eventually we will want to run this in characteristic 3, so
we need to: (a) Allow Q(x) to contain an 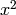 term, and
(b) Remove the requirement that 3 be invertible. Currently this is
used in the Toom-Cook algorithm to speed multiplication.
term, and
(b) Remove the requirement that 3 be invertible. Currently this is
used in the Toom-Cook algorithm to speed multiplication.
EXAMPLES:
sage: B.<t> = PolynomialRing(Integers(125))
sage: R = monsky_washnitzer.SpecialCubicQuotientRing(t^3 - t + B(1/4))
sage: R
SpecialCubicQuotientRing over Ring of integers modulo 125 with polynomial T = x^3 + 124*x + 94
Get generators:
sage: x, T = R.gens()
sage: x
(0) + (1)*x + (0)*x^2
sage: T
(T) + (0)*x + (0)*x^2
Coercions:
sage: R(7)
(7) + (0)*x + (0)*x^2
Create elements directly from polynomials:
sage: A, z = R.poly_ring().objgen()
sage: A
Univariate Polynomial Ring in T over Ring of integers modulo 125
sage: R.create_element(z^2, z+1, 3)
(T^2) + (T + 1)*x + (3)*x^2
Some arithmetic:
sage: x^3
(T + 31) + (1)*x + (0)*x^2
sage: 3 * x**15 * T**2 + x - T
(3*T^7 + 90*T^6 + 110*T^5 + 20*T^4 + 58*T^3 + 26*T^2 + 124*T) + (15*T^6 + 110*T^5 + 35*T^4 + 63*T^2 + 1)*x + (30*T^5 + 40*T^4 + 8*T^3 + 38*T^2)*x^2
Retrieve coefficients (output is zero-padded):
sage: x^10
(3*T^2 + 61*T + 8) + (T^3 + 93*T^2 + 12*T + 40)*x + (3*T^2 + 61*T + 9)*x^2
sage: (x^10).coeffs()
[[8, 61, 3, 0], [40, 12, 93, 1], [9, 61, 3, 0]]
TODO: write an example checking multiplication of these polynomials against Sage’s ordinary quotient ring arithmetic. I can’t seem to get the quotient ring stuff happening right now...
Creates the element  , where pi’s
are polynomials in T.
, where pi’s
are polynomials in T.
INPUT:
EXAMPLES:
sage: B.<t> = PolynomialRing(Integers(125))
sage: R = monsky_washnitzer.SpecialCubicQuotientRing(t^3 - t + B(1/4))
sage: A, z = R.poly_ring().objgen()
sage: R.create_element(z^2, z+1, 3)
(T^2) + (T + 1)*x + (3)*x^2
Return a list [x, T] where x and T are the generators of the ring (as element of this ring).
Note
I have no idea if this is compatible with the usual Sage ‘gens’ interface.
EXAMPLES:
sage: B.<t> = PolynomialRing(Integers(125))
sage: R = monsky_washnitzer.SpecialCubicQuotientRing(t^3 - t + B(1/4))
sage: x, T = R.gens()
sage: x
(0) + (1)*x + (0)*x^2
sage: T
(T) + (0)*x + (0)*x^2
Return the underlying polynomial ring in T.
EXAMPLES:
sage: B.<t> = PolynomialRing(Integers(125))
sage: R = monsky_washnitzer.SpecialCubicQuotientRing(t^3 - t + B(1/4))
sage: R.poly_ring()
Univariate Polynomial Ring in T over Ring of integers modulo 125
Bases: sage.structure.element.CommutativeAlgebraElement
An element of a SpecialCubicQuotientRing.
Returns list of three lists of coefficients, corresponding to the
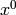 ,
, 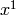 ,
, 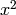 coefficients. The lists
are zero padded to the same length. The list entries belong to the
base ring.
coefficients. The lists
are zero padded to the same length. The list entries belong to the
base ring.
EXAMPLES:
sage: B.<t> = PolynomialRing(Integers(125))
sage: R = monsky_washnitzer.SpecialCubicQuotientRing(t^3 - t + B(1/4))
sage: p = R.create_element(t, t^2 - 2, 3)
sage: p.coeffs()
[[0, 1, 0], [123, 0, 1], [3, 0, 0]]
Multiplies this element by a scalar, i.e. just multiply each
coefficient of 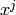 by the scalar.
by the scalar.
INPUT:
EXAMPLES:
sage: B.<t> = PolynomialRing(Integers(125))
sage: R = monsky_washnitzer.SpecialCubicQuotientRing(t^3 - t + B(1/4))
sage: x, T = R.gens()
sage: f = R.create_element(2, t, t^2 - 3)
sage: f
(2) + (T)*x + (T^2 + 122)*x^2
sage: f.scalar_multiply(2)
(4) + (2*T)*x + (2*T^2 + 119)*x^2
sage: f.scalar_multiply(t)
(2*T) + (T^2)*x + (T^3 + 122*T)*x^2
Returns this element multiplied by 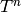 .
.
EXAMPLES:
sage: B.<t> = PolynomialRing(Integers(125))
sage: R = monsky_washnitzer.SpecialCubicQuotientRing(t^3 - t + B(1/4))
sage: f = R.create_element(2, t, t^2 - 3)
sage: f
(2) + (T)*x + (T^2 + 122)*x^2
sage: f.shift(1)
(2*T) + (T^2)*x + (T^3 + 122*T)*x^2
sage: f.shift(2)
(2*T^2) + (T^3)*x + (T^4 + 122*T^2)*x^2
EXAMPLES:
sage: B.<t> = PolynomialRing(Integers(125))
sage: R = monsky_washnitzer.SpecialCubicQuotientRing(t^3 - t + B(1/4))
sage: x, T = R.gens()
sage: f = R.create_element(1 + 2*t + 3*t^2, 4 + 7*t + 9*t^2, 3 + 5*t + 11*t^2)
sage: f.square()
(73*T^5 + 16*T^4 + 38*T^3 + 39*T^2 + 70*T + 120) + (121*T^5 + 113*T^4 + 73*T^3 + 8*T^2 + 51*T + 61)*x + (18*T^4 + 60*T^3 + 22*T^2 + 108*T + 31)*x^2
Bases: sage.structure.element.CommutativeAlgebraElement
Bases: sage.rings.ring.CommutativeAlgebra
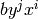 , computed quickly.
, computed quickly.The key here is that the formula for 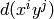 is messy
in terms of i, but varies nicely with j.
is messy
in terms of i, but varies nicely with j.
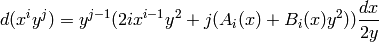
Where 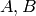 have degree at most
have degree at most 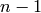 for each
for each
 . Pre-compute
. Pre-compute 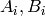 for each
for each  the “hard” way, and the rest are easy.
the “hard” way, and the rest are easy.
Computes how much precision is required in matrix_of_frobenius to
get an answer correct to prec  -adic digits.
-adic digits.
The issue is that the algorithm used in matrix_of_frobenius
sometimes performs divisions by  , so precision is lost
during the algorithm.
, so precision is lost
during the algorithm.
The estimate returned by this function is based on Kedlaya’s result
(Lemmas 2 and 3 of “Counting Points on Hyperelliptic Curves...”),
which implies that if we start with 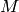
 -adic
digits, the total precision loss is at most
-adic
digits, the total precision loss is at most
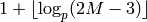
 -adic
digits. (This estimate is somewhat less than the amount you would
expect by naively counting the number of divisions by
-adic
digits. (This estimate is somewhat less than the amount you would
expect by naively counting the number of divisions by
 .)
.)
INPUT:
OUTPUT: adjusted precision (usually slightly more than prec)
Computes the action of Frobenius on 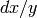 and on
and on
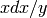 , using Newton’s method (as suggested in Kedlaya’s
paper).
, using Newton’s method (as suggested in Kedlaya’s
paper).
(This function does not yet use the cohomology relations - that happens afterwards in the “reduction” step.)
More specifically, it finds 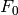 and
and 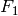 in
the quotient ring
in
the quotient ring ![R[x, T]/(T - Q(x))](../../../_images/math/cb90546b47669eb4f77427215f8264788807cd41.png) , such that
, such that
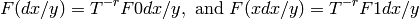
where
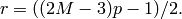
(Here 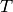 is
is 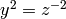 , and
, and 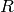 is the
coefficient ring of
is the
coefficient ring of 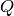 .)
.)
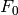 and
and 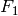 are computed in the
SpecialCubicQuotientRing associated to
are computed in the
SpecialCubicQuotientRing associated to 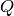 , so all powers
of
, so all powers
of 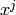 for
for 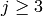 are reduced to powers of
are reduced to powers of
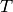 .
.
INPUT:
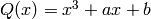 , whose coefficient ring is a
, whose coefficient ring is a
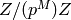 -algebra
-algebraOUTPUT:
Computes the action of Frobenius on dx/y and on x dx/y, using a series expansion.
(This function computes the same thing as frobenius_expansion_by_newton(), using a different method. Theoretically the Newton method should be asymptotically faster, when the precision gets large. However, in practice, this functions seems to be marginally faster for moderate precision, so I’m keeping it here until I figure out exactly why it’s faster.)
(This function does not yet use the cohomology relations - that happens afterwards in the “reduction” step.)
More specifically, it finds F0 and F1 in the quotient ring
![R[x, T]/(T - Q(x))](../../../_images/math/cb90546b47669eb4f77427215f8264788807cd41.png) , such that
, such that
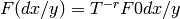 , and
, and
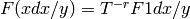 where
where
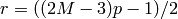 . (Here T is
. (Here T is 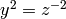 ,
and R is the coefficient ring of Q.)
,
and R is the coefficient ring of Q.)
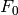 and
and 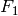 are computed in the
SpecialCubicQuotientRing associated to
are computed in the
SpecialCubicQuotientRing associated to 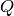 , so all powers
of
, so all powers
of 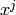 for
for 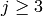 are reduced to powers of
are reduced to powers of
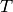 .
.
It uses the sum
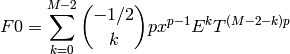
and
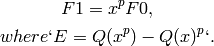
INPUT:
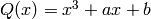 , whose coefficient ring is a
, whose coefficient ring is a
 -algebra
-algebraOUTPUT:
Computes the (constant) matrix used to calculate the linear
combinations of the 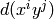 needed to eliminate the
negative powers of
needed to eliminate the
negative powers of 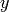 in the cohomology (i.e. in
reduce_negative()).
in the cohomology (i.e. in
reduce_negative()).
INPUT:
Tries to call x.lift(), presumably from the p-adics to ZZ.
If this fails, it assumes the input is a power series, and tries to lift it to a power series over QQ.
This function is just a very kludgy solution to the problem of trying to make the reduction code (below) work over both Zp and Zp[[t]].
Computes the matrix of Frobenius on Monsky-Washnitzer cohomology,
with respect to the basis 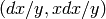 .
.
INPUT:
Q - cubic polynomial
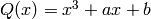 defining an elliptic curve E by
defining an elliptic curve E by
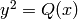 . The coefficient ring of Q should be a
. The coefficient ring of Q should be a
 -algebra in which the matrix of
frobenius will be constructed.
-algebra in which the matrix of
frobenius will be constructed.
p - prime = 5 for which E has good reduction
M - integer = 2;  -adic precision of
the coefficient ring
-adic precision of
the coefficient ring
trace - (optional) the trace of the matrix, if
known in advance. This is easy to compute because it’s just the
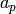 of the curve. If the trace is supplied,
matrix_of_frobenius will use it to speed the computation (i.e. we
know the determinant is
of the curve. If the trace is supplied,
matrix_of_frobenius will use it to speed the computation (i.e. we
know the determinant is  , so we have two conditions, so
really only column of the matrix needs to be computed. It’s
actually a little more complicated than that, but that’s the basic
idea.) If trace=None, then both columns will be computed
independently, and you can get a strong indication of correctness
by verifying the trace afterwards.
, so we have two conditions, so
really only column of the matrix needs to be computed. It’s
actually a little more complicated than that, but that’s the basic
idea.) If trace=None, then both columns will be computed
independently, and you can get a strong indication of correctness
by verifying the trace afterwards.
Warning
THE RESULT WILL NOT NECESSARILY BE CORRECT TO M p-ADIC
DIGITS. If you want prec digits of precision, you need to use
the function adjusted_prec(), and then you need to reduce the
answer mod 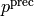 at the end.
at the end.
OUTPUT: 2x2 matrix of frobenius on Monsky-Washnitzer cohomology, with entries in the coefficient ring of Q.
EXAMPLES: A simple example:
sage: p = 5
sage: prec = 3
sage: M = monsky_washnitzer.adjusted_prec(p, prec)
sage: M
5
sage: R.<x> = PolynomialRing(Integers(p**M))
sage: A = monsky_washnitzer.matrix_of_frobenius(x^3 - x + R(1/4), p, M)
sage: A
[3090 187]
[2945 408]
But the result is only accurate to prec digits:
sage: B = A.change_ring(Integers(p**prec))
sage: B
[90 62]
[70 33]
Check trace (123 = -2 mod 125) and determinant:
sage: B.det()
5
sage: B.trace()
123
sage: EllipticCurve([-1, 1/4]).ap(5)
-2
Try using the trace to speed up the calculation:
sage: A = monsky_washnitzer.matrix_of_frobenius(x^3 - x + R(1/4),
... p, M, -2)
sage: A
[2715 187]
[1445 408]
Hmmm... it looks different, but that’s because the trace of our
first answer was only -2 modulo 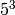 , not -2 modulo
, not -2 modulo
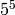 . So the right answer is:
. So the right answer is:
sage: A.change_ring(Integers(p**prec))
[90 62]
[70 33]
Check it works with only one digit of precision:
sage: p = 5
sage: prec = 1
sage: M = monsky_washnitzer.adjusted_prec(p, prec)
sage: R.<x> = PolynomialRing(Integers(p**M))
sage: A = monsky_washnitzer.matrix_of_frobenius(x^3 - x + R(1/4), p, M)
sage: A.change_ring(Integers(p))
[0 2]
[0 3]
Here’s an example that’s particularly badly conditioned for using the trace trick:
sage: p = 11
sage: prec = 3
sage: M = monsky_washnitzer.adjusted_prec(p, prec)
sage: R.<x> = PolynomialRing(Integers(p**M))
sage: A = monsky_washnitzer.matrix_of_frobenius(x^3 + 7*x + 8, p, M)
sage: A.change_ring(Integers(p**prec))
[1144 176]
[ 847 185]
The problem here is that the top-right entry is divisible by 11,
and the bottom-left entry is divisible by 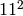 . So when
you apply the trace trick, neither
. So when
you apply the trace trick, neither 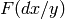 nor
nor
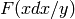 is enough to compute the whole matrix to the
desired precision, even if you try increasing the target precision
by one. Nevertheless, matrix_of_frobenius knows
how to get the right answer by evaluating
is enough to compute the whole matrix to the
desired precision, even if you try increasing the target precision
by one. Nevertheless, matrix_of_frobenius knows
how to get the right answer by evaluating 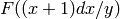 instead:
instead:
sage: A = monsky_washnitzer.matrix_of_frobenius(x^3 + 7*x + 8, p, M, -2)
sage: A.change_ring(Integers(p**prec))
[1144 176]
[ 847 185]
The running time is about O(p*prec**2) (times some logarithmic factors), so it’s feasible to run on fairly large primes, or precision (or both?!?!):
sage: p = 10007
sage: prec = 2
sage: M = monsky_washnitzer.adjusted_prec(p, prec)
sage: R.<x> = PolynomialRing(Integers(p**M))
sage: A = monsky_washnitzer.matrix_of_frobenius( # long time
... x^3 - x + R(1/4), p, M) # long time
sage: B = A.change_ring(Integers(p**prec)); B # long time
[74311982 57996908]
[95877067 25828133]
sage: B.det() # long time
10007
sage: B.trace() # long time
66
sage: EllipticCurve([-1, 1/4]).ap(10007) # long time
66
sage: p = 5
sage: prec = 300
sage: M = monsky_washnitzer.adjusted_prec(p, prec)
sage: R.<x> = PolynomialRing(Integers(p**M))
sage: A = monsky_washnitzer.matrix_of_frobenius( # long time
... x^3 - x + R(1/4), p, M) # long time
sage: B = A.change_ring(Integers(p**prec)) # long time
sage: B.det() # long time
5
sage: -B.trace() # long time
2
sage: EllipticCurve([-1, 1/4]).ap(5) # long time
-2
Let’s check consistency of the results for a range of precisions:
sage: p = 5
sage: max_prec = 60
sage: M = monsky_washnitzer.adjusted_prec(p, max_prec)
sage: R.<x> = PolynomialRing(Integers(p**M))
sage: A = monsky_washnitzer.matrix_of_frobenius(x^3 - x + R(1/4), p, M) # long time
sage: A = A.change_ring(Integers(p**max_prec)) # long time
sage: result = [] # long time
sage: for prec in range(1, max_prec): # long time
... M = monsky_washnitzer.adjusted_prec(p, prec) # long time
... R.<x> = PolynomialRing(Integers(p^M),'x') # long time
... B = monsky_washnitzer.matrix_of_frobenius( # long time
... x^3 - x + R(1/4), p, M) # long time
... B = B.change_ring(Integers(p**prec)) # long time
... result.append(B == A.change_ring( # long time
... Integers(p**prec))) # long time
sage: result == [True] * (max_prec - 1) # long time
True
The remaining examples discuss what happens when you take the coefficient ring to be a power series ring; i.e. in effect you’re looking at a family of curves.
The code does in fact work...
sage: p = 11
sage: prec = 3
sage: M = monsky_washnitzer.adjusted_prec(p, prec)
sage: S.<t> = PowerSeriesRing(Integers(p**M), default_prec=4)
sage: a = 7 + t + 3*t^2
sage: b = 8 - 6*t + 17*t^2
sage: R.<x> = PolynomialRing(S)
sage: Q = x**3 + a*x + b
sage: A = monsky_washnitzer.matrix_of_frobenius(Q, p, M) # long time
sage: B = A.change_ring(PowerSeriesRing(Integers(p**prec), 't', default_prec=4)) # long time
sage: B # long time
[1144 + 264*t + 841*t^2 + 1025*t^3 + O(t^4) 176 + 1052*t + 216*t^2 + 523*t^3 + O(t^4)]
[ 847 + 668*t + 81*t^2 + 424*t^3 + O(t^4) 185 + 341*t + 171*t^2 + 642*t^3 + O(t^4)]
The trace trick should work for power series rings too, even in the badly- conditioned case. Unfortunately I don’t know how to compute the trace in advance, so I’m not sure exactly how this would help. Also, I suspect the running time will be dominated by the expansion, so the trace trick won’t really speed things up anyway. Another problem is that the determinant is not always p:
sage: B.det() # long time
11 + 484*t^2 + 451*t^3 + O(t^4)
However, it appears that the determinant always has the property that if you substitute t - 11t, you do get the constant series p (mod p**prec). Similarly for the trace. And since the parameter only really makes sense when it’s divisible by p anyway, perhaps this isn’t a problem after all.
Applies cohomology relations to reduce all terms to a linear
combination of 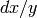 and
and 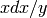 .
.
INPUT:
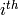 list [a, b, c] represents
list [a, b, c] represents
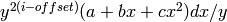 .
.OUTPUT:
Note
The algorithm operates in-place, so the data in coeffs is destroyed.
EXAMPLE:
sage: R.<x> = Integers(5^3)['x']
sage: Q = x^3 - x + R(1/4)
sage: coeffs = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
sage: coeffs = [[R.base_ring()(a) for a in row] for row in coeffs]
sage: monsky_washnitzer.reduce_all(Q, 5, coeffs, 1)
(21, 106)
Applies cohomology relations to incorporate negative powers of
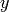 into the
into the 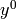 term.
term.
INPUT:
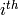 list [a, b, c] represents
list [a, b, c] represents
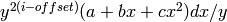 .
.OUTPUT: The reduction is performed in-place. The output is placed in coeffs[offset]. Note that coeffs[i] will be meaningless for i offset after this function is finished.
EXAMPLE:
sage: R.<x> = Integers(5^3)['x']
sage: Q = x^3 - x + R(1/4)
sage: coeffs = [[10, 15, 20], [1, 2, 3], [4, 5, 6], [7, 8, 9]]
sage: coeffs = [[R.base_ring()(a) for a in row] for row in coeffs]
sage: monsky_washnitzer.reduce_negative(Q, 5, coeffs, 3)
sage: coeffs[3]
[28, 52, 9]
sage: R.<x> = Integers(7^3)['x']
sage: Q = x^3 - x + R(1/4)
sage: coeffs = [[7, 14, 21], [1, 2, 3], [4, 5, 6], [7, 8, 9]]
sage: coeffs = [[R.base_ring()(a) for a in row] for row in coeffs]
sage: monsky_washnitzer.reduce_negative(Q, 7, coeffs, 3)
sage: coeffs[3]
[245, 332, 9]
Applies cohomology relations to incorporate positive powers of
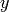 into the
into the 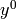 term.
term.
INPUT:
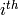 list [a, b, c] represents
list [a, b, c] represents
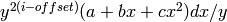 .
.OUTPUT: The reduction is performed in-place. The output is placed in coeffs[offset]. Note that coeffs[i] will be meaningless for i offset after this function is finished.
EXAMPLE:
sage: R.<x> = Integers(5^3)['x']
sage: Q = x^3 - x + R(1/4)
sage: coeffs = [[1, 2, 3], [10, 15, 20]]
sage: coeffs = [[R.base_ring()(a) for a in row] for row in coeffs]
sage: monsky_washnitzer.reduce_positive(Q, 5, coeffs, 0)
sage: coeffs[0]
[16, 102, 88]
sage: coeffs = [[9, 8, 7], [10, 15, 20]]
sage: coeffs = [[R.base_ring()(a) for a in row] for row in coeffs]
sage: monsky_washnitzer.reduce_positive(Q, 5, coeffs, 0)
sage: coeffs[0]
[24, 108, 92]
Applies cohomology relation to incorporate  term
into
term
into 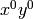 and
and 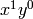 terms.
terms.
INPUT:
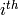 list [a, b, c] represents
list [a, b, c] represents
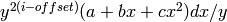 .
.OUTPUT: The reduction is performed in-place. The output is placed in coeffs[offset]. This method completely ignores coeffs[i] for i != offset.
EXAMPLE:
sage: R.<x> = Integers(5^3)['x']
sage: Q = x^3 - x + R(1/4)
sage: coeffs = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
sage: coeffs = [[R.base_ring()(a) for a in row] for row in coeffs]
sage: monsky_washnitzer.reduce_zero(Q, coeffs, 1)
sage: coeffs[1]
[6, 5, 0]
INPUT:
OUTPUT:
EXAMPLES:
sage: from sage.schemes.elliptic_curves.monsky_washnitzer import transpose_list
sage: L = [[1, 2], [3, 4], [5, 6]]
sage: transpose_list(L)
[[1, 3, 5], [2, 4, 6]]