To an elliptic curve  over the rational numbers and a prime
over the rational numbers and a prime  , one
can associate a
, one
can associate a  -adic L-function; at least if
-adic L-function; at least if  does not have additive
reduction at
does not have additive
reduction at  .
This function is defined by interpolation of L-values of
.
This function is defined by interpolation of L-values of  at twists. Through
the main conjecture of Iwasawa theory it should also be equal to a characteristic
series of a certain Selmer group.
at twists. Through
the main conjecture of Iwasawa theory it should also be equal to a characteristic
series of a certain Selmer group.
If  is ordinary, then it is an element of
is ordinary, then it is an element of ![\ZZ_p[\![T]\!]](../../../_images/math/e21dac9b52c44ba125999ac40486c7f81fe47eb0.png) and according to the
and according to the
 -adic version of the Birch and Swinnerton-Dyer conjecture [MTT], the order of
vanishing at
-adic version of the Birch and Swinnerton-Dyer conjecture [MTT], the order of
vanishing at 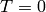 is just the rank of
is just the rank of 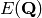 or this rank plus one if the reduction
at
or this rank plus one if the reduction
at  is split multiplicative.
is split multiplicative.
If  is supersingular, the series will have coefficients in a quadratic
extension of
is supersingular, the series will have coefficients in a quadratic
extension of 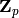 . We have also implemented the
. We have also implemented the  -adic L-series
as formulated by Perrin-Riou [BP], which has coefficients in the
Dieudonne
-adic L-series
as formulated by Perrin-Riou [BP], which has coefficients in the
Dieudonne 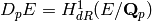 module of
module of  . There is a different description by Pollack [Po]
which is not available here.
. There is a different description by Pollack [Po]
which is not available here.
See [SW] for more details.
REFERENCES:
 -adic analogues of the conjectures of Birch and
Swinnerton-Dyer, Inventiones mathematicae 84, (1986), 1-48.
-adic analogues of the conjectures of Birch and
Swinnerton-Dyer, Inventiones mathematicae 84, (1986), 1-48. -adique de la conjecture de Birch et
Swinnerton-Dyer (le cas supersingulier), C. R. Acad. Sci. Paris,
Ser I. Math, 317 (1993), no 3, 227-232.
-adique de la conjecture de Birch et
Swinnerton-Dyer (le cas supersingulier), C. R. Acad. Sci. Paris,
Ser I. Math, 317 (1993), no 3, 227-232. -adic L-function of a modular form
at supersingular prime, Duke Math. J. 118 (2003), no 3, 523-558.
-adic L-function of a modular form
at supersingular prime, Duke Math. J. 118 (2003), no 3, 523-558.AUTHORS:
Bases: sage.structure.sage_object.SageObject
The  -adic L-series of an elliptic curve.
-adic L-series of an elliptic curve.
EXAMPLES: An ordinary example:
sage: e = EllipticCurve('389a')
sage: L = e.padic_lseries(5)
sage: L.series(0)
...
ValueError: n (=0) must be a positive integer
sage: L.series(1)
O(T^1)
sage: L.series(2)
O(5^4) + O(5)*T + (4 + O(5))*T^2 + (2 + O(5))*T^3 + (3 + O(5))*T^4 + O(T^5)
sage: L.series(3, prec=10)
O(5^5) + O(5^2)*T + (4 + 4*5 + O(5^2))*T^2 + (2 + 4*5 + O(5^2))*T^3 + (3 + O(5^2))*T^4 + (1 + O(5))*T^5 + (3*5 + O(5^2))*T^6 + (4 + 5 + O(5^2))*T^7 + (2 + 5 + O(5^2))*T^8 + O(5^2)*T^9 + O(T^10)
sage: L.series(2,quadratic_twist=-3)
2 + 4*5 + 4*5^2 + O(5^4) + O(5)*T + (1 + O(5))*T^2 + (4 + O(5))*T^3 + O(5)*T^4 + O(T^5)
A prime p such that E[p] is reducible:
sage: L = EllipticCurve('11a').padic_lseries(5)
sage: L.series(1)
5 + O(5^2) + O(T)
sage: L.series(2)
5 + 4*5^2 + O(5^3) + O(5^0)*T + O(5^0)*T^2 + O(5^0)*T^3 + O(5^0)*T^4 + O(T^5)
sage: L.series(3)
5 + 4*5^2 + 4*5^3 + O(5^4) + O(5)*T + O(5)*T^2 + O(5)*T^3 + O(5)*T^4 + O(T^5)
the load-dumps test:
sage: lp = EllipticCurve('11a').padic_lseries(5)
sage: lp == loads(dumps(lp))
True
Return a  -adic root
-adic root 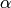 of the polynomial
of the polynomial 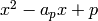 with
with 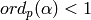 . In the ordinary case this is
just the unit root.
. In the ordinary case this is
just the unit root.
INPUT:
- prec - positive integer, the  -adic precision of the root.
-adic precision of the root.
EXAMPLES: Consider the elliptic curve 37a:
sage: E = EllipticCurve('37a')
An ordinary prime:
sage: L = E.padic_lseries(5)
sage: alpha = L.alpha(10); alpha
3 + 2*5 + 4*5^2 + 2*5^3 + 5^4 + 4*5^5 + 2*5^7 + 5^8 + 5^9 + O(5^10)
sage: alpha^2 - E.ap(5)*alpha + 5
O(5^10)
A supersingular prime:
sage: L = E.padic_lseries(3)
sage: alpha = L.alpha(10); alpha
(1 + O(3^10))*alpha
sage: alpha^2 - E.ap(3)*alpha + 3
(O(3^10))*alpha^2 + (O(3^11))*alpha + (O(3^11))
A reducible prime:
sage: L = EllipticCurve('11a').padic_lseries(5)
sage: L.alpha(5)
1 + 4*5 + 3*5^2 + 2*5^3 + 4*5^4 + O(5^5)
Return the elliptic curve to which this  -adic L-series is associated.
-adic L-series is associated.
EXAMPLES:
sage: L = EllipticCurve('11a').padic_lseries(5)
sage: L.elliptic_curve()
Elliptic Curve defined by y^2 + y = x^3 - x^2 - 10*x - 20 over Rational Field
Return the measure on  defined by
defined by
where ![[\cdot]^{+}](../../../_images/math/7970b9366ebada9037a88275c026704a7b9027f8.png) is the modular symbol. This is used to define
this
is the modular symbol. This is used to define
this  -adic L-function (at least when the reduction is good).
-adic L-function (at least when the reduction is good).
The optional argument quadratic_twist replaces  by the twist in the above formula,
but the twisted modular symbol is computed using a sum over modular symbols of
by the twist in the above formula,
but the twisted modular symbol is computed using a sum over modular symbols of  rather then finding the modular symbols for the twist.
rather then finding the modular symbols for the twist.
Note that the normalisation is not correct at this stage: use _quotient_of periods and _quotient_of periods_to_twist to correct.
Note also that this function does not check if the condition
on the quadratic_twist=D is satisfied. So the result will only
be correct if for each prime 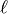 dividing
dividing  , we have
, we have
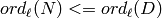 , where
, where  is the conductor of the curve.
is the conductor of the curve.
INPUT:

EXAMPLES:
sage: E = EllipticCurve('37a')
sage: L = E.padic_lseries(5)
sage: L.measure(1,2, prec=9)
2 + 3*5 + 4*5^3 + 2*5^4 + 3*5^5 + 3*5^6 + 4*5^7 + 4*5^8 + O(5^9)
sage: L.measure(1,2, quadratic_twist=8,prec=15)
O(5^15)
sage: L.measure(1,2, quadratic_twist=-4,prec=15)
4 + 4*5 + 4*5^2 + 3*5^3 + 2*5^4 + 5^5 + 3*5^6 + 5^8 + 2*5^9 + 3*5^12 + 2*5^13 + 4*5^14 + O(5^15)
sage: E = EllipticCurve('11a1')
sage: a = E.quadratic_twist(-3).padic_lseries(5).measure(1,2,prec=15)
sage: b = E.padic_lseries(5).measure(1,2, quadratic_twist=-3,prec=15)
sage: a == b/E.padic_lseries(5)._quotient_of_periods_to_twist(-3)
True
Return the modular symbol evaluated at  .
This is used to compute this
.
This is used to compute this  -adic
L-series.
-adic
L-series.
Note that the normalisation is not correct at this stage: use _quotient_of periods_to_twist to correct.
Note also that this function does not check if the condition
on the quadratic_twist=D is satisfied. So the result will only
be correct if for each prime 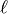 dividing
dividing  , we have
, we have
 , where
, where  is the conductor of the curve.
is the conductor of the curve.
INPUT:
EXAMPLES:
sage: E = EllipticCurve('11a1')
sage: lp = E.padic_lseries(5)
sage: [lp.modular_symbol(r) for r in [0,1/5,oo,1/11]]
[1/5, 6/5, 0, 0]
sage: [lp.modular_symbol(r,sign=-1) for r in [0,1/3,oo,1/7]]
[0, 1, 0, -1]
sage: [lp.modular_symbol(r,quadratic_twist=-20) for r in [0,1/5,oo,1/11]]
[2, 2, 0, 1]
sage: lpt = E.quadratic_twist(-3).padic_lseries(5)
sage: et = E.padic_lseries(5)._quotient_of_periods_to_twist(-3)
sage: lpt.modular_symbol(0) == lp.modular_symbol(0,quadratic_twist=-3)/et
True
Return the order of vanishing of this  -adic L-series.
-adic L-series.
The output of this function is provably correct, due to a
theorem of Kato [Ka]. This function will terminate if and only if
the Mazur-Tate-Teitelbaum analogue [MTT] of the BSD conjecture about
the rank of the curve is true and the subgroup of elements of
 -power order in the Shafarevich-Tate group of this curve is
finite. I.e. if this function terminates (with no errors!),
then you may conclude that the
-power order in the Shafarevich-Tate group of this curve is
finite. I.e. if this function terminates (with no errors!),
then you may conclude that the  -adic BSD rank conjecture is
true and that the
-adic BSD rank conjecture is
true and that the  -part of Sha is finite.
-part of Sha is finite.
NOTE: currently  must be a prime of good ordinary reduction.
must be a prime of good ordinary reduction.
REFERENCES:
 -adic analogues of the conjectures of Birch and
Swinnerton-Dyer, Inventiones mathematicae 84, (1986), 1-48.
-adic analogues of the conjectures of Birch and
Swinnerton-Dyer, Inventiones mathematicae 84, (1986), 1-48. -adic Hodge theory and values of zeta functions of modular
forms, Cohomologies
-adic Hodge theory and values of zeta functions of modular
forms, Cohomologies  -adiques et applications arithmetiques III,
Asterisque vol 295, SMF, Paris, 2004.
-adiques et applications arithmetiques III,
Asterisque vol 295, SMF, Paris, 2004.EXAMPLES:
sage: L = EllipticCurve('11a').padic_lseries(3)
sage: L.order_of_vanishing()
0
sage: L = EllipticCurve('11a').padic_lseries(5)
sage: L.order_of_vanishing()
0
sage: L = EllipticCurve('37a').padic_lseries(5)
sage: L.order_of_vanishing()
1
sage: L = EllipticCurve('43a').padic_lseries(3)
sage: L.order_of_vanishing()
1
sage: L = EllipticCurve('37b').padic_lseries(3)
sage: L.order_of_vanishing()
0
We verify that Sha(E)(p) is finite for p=3,5,7 for the first curve of rank 2:
sage: e = EllipticCurve('389a')
sage: for p in primes(3,10):
... print p, e.padic_lseries(p).order_of_vanishing()
3 2
5 2
7 2
Returns the prime  as in ‘p-adic L-function’.
as in ‘p-adic L-function’.
EXAMPLES:
sage: L = EllipticCurve('11a').padic_lseries(5)
sage: L.prime()
5
Return Teichmuller lifts to the given precision.
INPUT:
OUTPUT:
 -adic numbers, the cached Teichmuller lifts
-adic numbers, the cached Teichmuller liftsEXAMPLES:
sage: L = EllipticCurve('11a').padic_lseries(7)
sage: L.teichmuller(1)
[0, 1, 2, 3, 4, 5, 6]
sage: L.teichmuller(2)
[0, 1, 30, 31, 18, 19, 48]
Bases: sage.schemes.elliptic_curves.padic_lseries.pAdicLseries
Return True if the elliptic that this L-function is attached to is ordinary.
EXAMPLES:
sage: L = EllipticCurve('11a').padic_lseries(5)
sage: L.is_ordinary()
True
Return True if the elliptic that this L function is attached to is supersingular.
EXAMPLES:
sage: L = EllipticCurve('11a').padic_lseries(5)
sage: L.is_supersingular()
False
Returns the  -th approximation to the
-th approximation to the  -adic L-series as
a power series in
-adic L-series as
a power series in 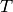 (corresponding to
(corresponding to 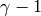 with
with
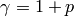 as a generator of
as a generator of 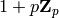 ). Each
coefficient is a
). Each
coefficient is a  -adic number whose precision is provably
correct.
-adic number whose precision is provably
correct.
Here the normalization of the  -adic L-series is chosen
such that
-adic L-series is chosen
such that 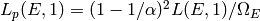 where
where 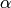 is the unit root of the characteristic
polynomial of Frobenius on
is the unit root of the characteristic
polynomial of Frobenius on 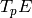 and
and 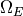 is the
Neron period of
is the
Neron period of  .
.
INPUT:
ALIAS: power_series is identical to series.
EXAMPLES:
We compute some  -adic L-functions associated to the elliptic
curve 11a:
-adic L-functions associated to the elliptic
curve 11a:
sage: E = EllipticCurve('11a')
sage: p = 3
sage: E.is_ordinary(p)
True
sage: L = E.padic_lseries(p)
sage: L.series(3)
2 + 3 + 3^2 + 2*3^3 + O(3^5) + (1 + 3 + O(3^2))*T + (1 + 2*3 + O(3^2))*T^2 + O(3)*T^3 + (2*3 + O(3^2))*T^4 + O(T^5)
Another example at a prime of bad reduction, where the
 -adic L-function has an extra 0 (compared to the non
-adic L-function has an extra 0 (compared to the non
 -adic L-function):
-adic L-function):
sage: E = EllipticCurve('11a')
sage: p = 11
sage: E.is_ordinary(p)
True
sage: L = E.padic_lseries(p)
sage: L.series(2)
O(11^4) + (10 + O(11))*T + (6 + O(11))*T^2 + (2 + O(11))*T^3 + (5 + O(11))*T^4 + O(T^5)
We compute a  -adic L-function that vanishes to order 2:
-adic L-function that vanishes to order 2:
sage: E = EllipticCurve('389a')
sage: p = 3
sage: E.is_ordinary(p)
True
sage: L = E.padic_lseries(p)
sage: L.series(1)
O(T^1)
sage: L.series(2)
O(3^4) + O(3)*T + (2 + O(3))*T^2 + O(T^3)
sage: L.series(3)
O(3^5) + O(3^2)*T + (2 + 2*3 + O(3^2))*T^2 + (2 + O(3))*T^3 + (1 + 3 + O(3^2))*T^4 + O(T^5)
Checks if the precision can be changed (trac 5846):
sage: L.series(3,prec=4)
O(3^5) + O(3^2)*T + (2 + 2*3 + O(3^2))*T^2 + (2 + O(3))*T^3 + O(T^4)
sage: L.series(3,prec=6)
O(3^5) + O(3^2)*T + (2 + 2*3 + O(3^2))*T^2 + (2 + O(3))*T^3 + (1 + 3 + O(3^2))*T^4 + (1 + O(3^2))*T^5 + O(T^6)
Rather than computing the  -adic L-function for the curve ‘15523a1’, one can
compute it as a quadratic_twist:
-adic L-function for the curve ‘15523a1’, one can
compute it as a quadratic_twist:
sage: E = EllipticCurve('43a1')
sage: lp = E.padic_lseries(3)
sage: lp.series(2,quadratic_twist=-19)
2 + 2*3 + 2*3^2 + O(3^4) + (1 + O(3))*T + (1 + O(3))*T^2 + O(T^3)
sage: E.quadratic_twist(-19).label() #optional --- conductor is greater than 10000
'15523a1'
This proves that the rank of ‘15523a1’ is zero, even if mwrank can not determine this.
Returns the  -th approximation to the
-th approximation to the  -adic L-series as
a power series in
-adic L-series as
a power series in 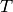 (corresponding to
(corresponding to 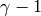 with
with
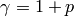 as a generator of
as a generator of 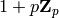 ). Each
coefficient is a
). Each
coefficient is a  -adic number whose precision is provably
correct.
-adic number whose precision is provably
correct.
Here the normalization of the  -adic L-series is chosen
such that
-adic L-series is chosen
such that 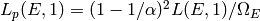 where
where 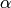 is the unit root of the characteristic
polynomial of Frobenius on
is the unit root of the characteristic
polynomial of Frobenius on 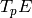 and
and 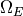 is the
Neron period of
is the
Neron period of  .
.
INPUT:
ALIAS: power_series is identical to series.
EXAMPLES:
We compute some  -adic L-functions associated to the elliptic
curve 11a:
-adic L-functions associated to the elliptic
curve 11a:
sage: E = EllipticCurve('11a')
sage: p = 3
sage: E.is_ordinary(p)
True
sage: L = E.padic_lseries(p)
sage: L.series(3)
2 + 3 + 3^2 + 2*3^3 + O(3^5) + (1 + 3 + O(3^2))*T + (1 + 2*3 + O(3^2))*T^2 + O(3)*T^3 + (2*3 + O(3^2))*T^4 + O(T^5)
Another example at a prime of bad reduction, where the
 -adic L-function has an extra 0 (compared to the non
-adic L-function has an extra 0 (compared to the non
 -adic L-function):
-adic L-function):
sage: E = EllipticCurve('11a')
sage: p = 11
sage: E.is_ordinary(p)
True
sage: L = E.padic_lseries(p)
sage: L.series(2)
O(11^4) + (10 + O(11))*T + (6 + O(11))*T^2 + (2 + O(11))*T^3 + (5 + O(11))*T^4 + O(T^5)
We compute a  -adic L-function that vanishes to order 2:
-adic L-function that vanishes to order 2:
sage: E = EllipticCurve('389a')
sage: p = 3
sage: E.is_ordinary(p)
True
sage: L = E.padic_lseries(p)
sage: L.series(1)
O(T^1)
sage: L.series(2)
O(3^4) + O(3)*T + (2 + O(3))*T^2 + O(T^3)
sage: L.series(3)
O(3^5) + O(3^2)*T + (2 + 2*3 + O(3^2))*T^2 + (2 + O(3))*T^3 + (1 + 3 + O(3^2))*T^4 + O(T^5)
Checks if the precision can be changed (trac 5846):
sage: L.series(3,prec=4)
O(3^5) + O(3^2)*T + (2 + 2*3 + O(3^2))*T^2 + (2 + O(3))*T^3 + O(T^4)
sage: L.series(3,prec=6)
O(3^5) + O(3^2)*T + (2 + 2*3 + O(3^2))*T^2 + (2 + O(3))*T^3 + (1 + 3 + O(3^2))*T^4 + (1 + O(3^2))*T^5 + O(T^6)
Rather than computing the  -adic L-function for the curve ‘15523a1’, one can
compute it as a quadratic_twist:
-adic L-function for the curve ‘15523a1’, one can
compute it as a quadratic_twist:
sage: E = EllipticCurve('43a1')
sage: lp = E.padic_lseries(3)
sage: lp.series(2,quadratic_twist=-19)
2 + 2*3 + 2*3^2 + O(3^4) + (1 + O(3))*T + (1 + O(3))*T^2 + O(T^3)
sage: E.quadratic_twist(-19).label() #optional --- conductor is greater than 10000
'15523a1'
This proves that the rank of ‘15523a1’ is zero, even if mwrank can not determine this.
Bases: sage.schemes.elliptic_curves.padic_lseries.pAdicLseries
Returns the canonical  -adic height with values in the Dieudonne module
-adic height with values in the Dieudonne module 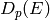 .
It is defined to be
.
It is defined to be
where 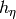 is made out of the sigma function of Bernardi and
is made out of the sigma function of Bernardi and
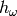 is
is 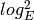 .
The answer v is given as v[1]*omega + v[2]*eta.
The coordinates of v are dependent of the
Weierstrass equation.
.
The answer v is given as v[1]*omega + v[2]*eta.
The coordinates of v are dependent of the
Weierstrass equation.
EXAMPLES:
sage: E = EllipticCurve('53a')
sage: L = E.padic_lseries(5)
sage: h = L.Dp_valued_height(7)
sage: h(E.gens()[0])
(3*5 + 5^2 + 2*5^3 + 3*5^4 + 4*5^5 + 5^6 + 5^7 + O(5^8), 5^2 + 4*5^4 + 2*5^7 + 3*5^8 + O(5^9))
Returns the canonical  -adic regulator with values in the Dieudonne module
-adic regulator with values in the Dieudonne module 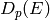 as defined by Perrin-Riou using the
as defined by Perrin-Riou using the  -adic height with values in
-adic height with values in 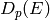 .
The result is written in the basis
.
The result is written in the basis 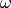 ,
, 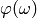 , and hence the
coordinates of the result are independent of the chosen Weierstrass equation.
, and hence the
coordinates of the result are independent of the chosen Weierstrass equation.
NOTE: The definition here is corrected with respect to Perrin-Riou’s article [PR]. See [SW].
REFERENCES:
 ,
Experiment. Math. 12 (2003), no. 2, 155-186.
,
Experiment. Math. 12 (2003), no. 2, 155-186.EXAMPLES:
sage: E = EllipticCurve('43a')
sage: L = E.padic_lseries(7)
sage: L.Dp_valued_regulator(7)
(5*7 + 6*7^2 + 4*7^3 + 4*7^4 + 7^5 + 4*7^7 + O(7^8), 4*7^2 + 2*7^3 + 3*7^4 + 7^5 + 6*7^6 + 4*7^7 + O(7^8))
Returns a vector of two components which are p-adic power series. The answer v is such that
v[1]
v[2]
as an element of the Dieudonne module 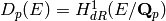 where
where
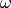 is the invariant differential and
is the invariant differential and  is the Frobenius on
is the Frobenius on 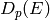 .
According to the
.
According to the  -adic Birch and Swinnerton-Dyer
conjecture [BP] this function has a zero of order
rank of
-adic Birch and Swinnerton-Dyer
conjecture [BP] this function has a zero of order
rank of 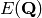 and it’s leading term is contains the order of
the Tate-Shafarevich group, the Tamagawa numbers, the order of the
torsion subgroup and the
and it’s leading term is contains the order of
the Tate-Shafarevich group, the Tamagawa numbers, the order of the
torsion subgroup and the 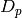 -valued
-valued  -adic regulator.
-adic regulator.
INPUT:
REFERENCE:
 -adique de la conjecture de Birch et
Swinnerton-Dyer (le cas supersingulier), C. R. Acad. Sci. Paris,
Ser I. Math, 317 (1993), no 3, 227-232.
-adique de la conjecture de Birch et
Swinnerton-Dyer (le cas supersingulier), C. R. Acad. Sci. Paris,
Ser I. Math, 317 (1993), no 3, 227-232.EXAMPLES:
sage: E = EllipticCurve('14a')
sage: L = E.padic_lseries(5)
sage: L.Dp_valued_series(4)
(1 + 4*5 + 4*5^3 + O(5^4) + (4 + O(5))*T + (1 + O(5))*T^2 + (4 + O(5))*T^3 + (2 + O(5))*T^4 + O(T^5), O(5^4) + O(5)*T + O(5)*T^2 + O(5)*T^3 + (2 + O(5))*T^4 + O(T^5))
Return the  -adic sigma function of Bernardi in terms of
-adic sigma function of Bernardi in terms of 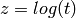 .
This is the same as padic_sigma with E2 = 0.
.
This is the same as padic_sigma with E2 = 0.
EXAMPLES:
sage: E = EllipticCurve('14a')
sage: L = E.padic_lseries(5)
sage: L.bernardi_sigma_function(5) # Todo: some sort of consistency check!?
z + 1/24*z^3 + 29/384*z^5 - 8399/322560*z^7 - 291743/92897280*z^9 - 4364831/5225472*z^10 + 2172371753/955514880*z^11 - 17875714529/6897623040*z^12 + 2839176621047/1605264998400*z^13 + 32012675789849/10042939146240*z^14 - 367444910151047/89894839910400*z^15 + 973773806885959/241030539509760*z^16 - 33997971208432501/17259809262796800*z^17 - 10331978660756704339/842918229599846400*z^18 + 18601407947897364480389/950670294194847744000*z^19 - 118837570440101901119321/8071784966648129126400*z^20 + O(z^21)
This returns a geometric Frobenius  on the Diedonne module
on the Diedonne module 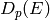 with respect to the basis
with respect to the basis 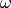 , the invariant differential, and
, the invariant differential, and 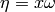 .
It satisfies
.
It satisfies 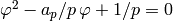 .
.
INPUT:
EXAMPLES:
sage: E = EllipticCurve('14a')
sage: L = E.padic_lseries(5)
sage: phi = L.frobenius(5)
sage: phi
[ 2 + 5^2 + 5^4 + O(5^5) 3*5^-1 + 3 + 5 + 4*5^2 + 5^3 + O(5^4)]
[ 3 + 3*5^2 + 4*5^3 + 3*5^4 + O(5^5) 3 + 4*5 + 3*5^2 + 4*5^3 + 3*5^4 + O(5^5)]
sage: -phi^2
[5^-1 + O(5^4) O(5^4)]
[ O(5^5) 5^-1 + O(5^4)]
Return the  -th approximation to the
-th approximation to the  -adic L-series as a
power series in
-adic L-series as a
power series in 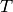 (corresponding to
(corresponding to 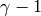 with
with
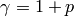 as a generator of
as a generator of 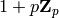 ). Each
coefficient is an element of a quadratic extension of the
). Each
coefficient is an element of a quadratic extension of the  -adic
number whose precision is probably correct.
-adic
number whose precision is probably correct.
Here the normalization of the  -adic L-series is chosen
such that
-adic L-series is chosen
such that 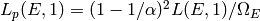 where
where 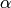 is the unit root of the characteristic
polynomial of Frobenius on
is the unit root of the characteristic
polynomial of Frobenius on 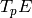 and
and 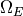 is the
Neron period of
is the
Neron period of  .
.
INPUT:
ALIAS: power_series is identical to series.
EXAMPLES: A superingular example, where we must compute to higher precision to see anything:
sage: e = EllipticCurve('37a')
sage: L = e.padic_lseries(3); L
3-adic L-series of Elliptic Curve defined by y^2 + y = x^3 - x over Rational Field
sage: L.series(2)
O(T^3)
sage: L.series(4) # takes a long time (several seconds)
(O(3))*alpha + (O(3^2)) + ((O(3^-1))*alpha + (2*3^-1 + O(3^0)))*T + ((O(3^-1))*alpha + (2*3^-1 + O(3^0)))*T^2 + ((O(3^-2))*alpha + (O(3^-1)))*T^3 + ((O(3^-1))*alpha + (3^-1 + O(3^0)))*T^4 + O(T^5)
sage: L.alpha(2).parent()
Univariate Quotient Polynomial Ring in alpha over 3-adic Field with capped
relative precision 2 with modulus (1 + O(3^2))*x^2 + (3 + O(3^3))*x + (3 + O(3^3))
Return the  -th approximation to the
-th approximation to the  -adic L-series as a
power series in
-adic L-series as a
power series in 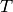 (corresponding to
(corresponding to 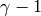 with
with
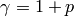 as a generator of
as a generator of 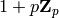 ). Each
coefficient is an element of a quadratic extension of the
). Each
coefficient is an element of a quadratic extension of the  -adic
number whose precision is probably correct.
-adic
number whose precision is probably correct.
Here the normalization of the  -adic L-series is chosen
such that
-adic L-series is chosen
such that 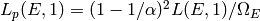 where
where 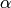 is the unit root of the characteristic
polynomial of Frobenius on
is the unit root of the characteristic
polynomial of Frobenius on 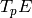 and
and 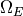 is the
Neron period of
is the
Neron period of  .
.
INPUT:
ALIAS: power_series is identical to series.
EXAMPLES: A superingular example, where we must compute to higher precision to see anything:
sage: e = EllipticCurve('37a')
sage: L = e.padic_lseries(3); L
3-adic L-series of Elliptic Curve defined by y^2 + y = x^3 - x over Rational Field
sage: L.series(2)
O(T^3)
sage: L.series(4) # takes a long time (several seconds)
(O(3))*alpha + (O(3^2)) + ((O(3^-1))*alpha + (2*3^-1 + O(3^0)))*T + ((O(3^-1))*alpha + (2*3^-1 + O(3^0)))*T^2 + ((O(3^-2))*alpha + (O(3^-1)))*T^3 + ((O(3^-1))*alpha + (3^-1 + O(3^0)))*T^4 + O(T^5)
sage: L.alpha(2).parent()
Univariate Quotient Polynomial Ring in alpha over 3-adic Field with capped
relative precision 2 with modulus (1 + O(3^2))*x^2 + (3 + O(3^3))*x + (3 + O(3^3))