Rings¶

This module provides the abstract base class Ring from which all rings in Sage are derived, as well as a selection of more specific base classes. The class inheritance hierarchy is:

Ring
- Algebra
- CommutativeRing

Subclasses of PrincipalIdealDomain are

EuclideanDomain
Field
- FiniteField

Some aspects of this structure may seem strange, but this is an unfortunate consequence of the fact that Cython classes do not support multiple inheritance. Hence, for instance, Field cannot be a subclass of both NoetherianRing and PrincipalIdealDomain, although all fields are Noetherian PIDs.

(A distinct but equally awkward issue is that sometimes we may not know in advance whether or not a ring belongs in one of these classes; e.g. some orders in number fields are Dedekind domains, but others are not, and we still want to offer a unified interface, so orders are never instances of the DedekindDomain class.)

AUTHORS:

David Harvey (2006-10-16): changed CommutativeAlgebra to derive from CommutativeRing instead of from Algebra
David Loeffler (2009-07-09): documentation fixes, added to reference manual

class sage.rings.ring.Algebra¶

Bases: sage.rings.ring.Ring

Generic algebra

characteristic()¶

Return the characteristic of this algebra, which is the same as the characteristic of its base ring.

See objects with the base_ring attribute for additional examples. Here are some examples that explicitly use the Algebra class.

EXAMPLES:

sage: A = Algebra(ZZ); A
<type 'sage.rings.ring.Algebra'>
sage: A.characteristic()
0
sage: A = Algebra(GF(7^3, 'a'))
sage: A.characteristic()
7

class sage.rings.ring.CommutativeAlgebra¶

Bases: sage.rings.ring.CommutativeRing

Generic commutative algebra

is_commutative()¶

Return True since this algebra is commutative.

EXAMPLES:

Any commutative ring is a commutative algebra over itself:

sage: A = sage.rings.ring.CommutativeAlgebra
sage: A(ZZ).is_commutative()
True
sage: A(QQ).is_commutative()
True

Trying to create a commutative algebra over a non-commutative ring will result in a TypeError.

class sage.rings.ring.CommutativeRing¶

Bases: sage.rings.ring.Ring

Generic commutative ring.

category()¶

Return the category to which this ring belongs.

EXAMPLES:: sage: QQ[‘x,y’].category() Category of commutative rings

extension(poly, name=None, names=None, embedding=None)¶

Algebraically extends self by taking the quotient self[x] / (f(x)).

INPUT:

poly – A polynomial whose coefficients are coercible into self
name – (optional) name for the root of f

EXAMPLES:

sage: R = QQ['x']
sage: y = polygen(R)
sage: R.extension(y^2-5, 'a')
Univariate Quotient Polynomial Ring in a over Univariate Polynomial Ring in x over Rational Field with modulus a^2 - 5

fraction_field()¶

Return the fraction field of self.

EXAMPLES:

sage: R = Integers(389)['x,y']
sage: Frac(R)
Fraction Field of Multivariate Polynomial Ring in x, y over Ring of integers modulo 389
sage: R.fraction_field()
Fraction Field of Multivariate Polynomial Ring in x, y over Ring of integers modulo 389            

ideal_monoid()¶

Return the monoid of ideals of this ring.

EXAMPLES:

sage: ZZ.ideal_monoid()
Monoid of ideals of Integer Ring
sage: R.<x>=QQ[]; R.ideal_monoid()
Monoid of ideals of Univariate Polynomial Ring in x over Rational Field

is_commutative()¶

Return True, since this ring is commutative.

EXAMPLES:

sage: QQ.is_commutative()
True
sage: ZpCA(7).is_commutative()
True
sage: A = QuaternionAlgebra(QQ, -1, -3, names=('i','j','k')); A
Quaternion Algebra (-1, -3) with base ring Rational Field
sage: A.is_commutative()
False

krull_dimension()¶

Return the Krull dimension of this commutative ring.

The Krull dimension is the length of the longest ascending chain of prime ideals.

TESTS:

krull_dimension is not implemented for generic commutative rings. Fields and PIDs, with Krull dimension equal to 0 and 1, respectively, have naive implementations of krull_dimension. Orders in number fields also have Krull dimension 1:

sage: R = CommutativeRing(ZZ)
sage: R.krull_dimension()
...
NotImplementedError
sage: QQ.krull_dimension()
0
sage: ZZ.krull_dimension()
1
sage: type(R); type(QQ); type(ZZ)
<type 'sage.rings.ring.CommutativeRing'>
<class 'sage.rings.rational_field.RationalField_with_category'>
<type 'sage.rings.integer_ring.IntegerRing_class'>

All orders in number fields have Krull dimension 1, including non-maximal orders:

sage: K.<i> = QuadraticField(-1)
sage: R = K.maximal_order(); R
Maximal Order in Number Field in i with defining polynomial x^2 + 1
sage: R.krull_dimension()
1
sage: R = K.order(2*i); R
Order in Number Field in i with defining polynomial x^2 + 1
sage: R.is_maximal()
False
sage: R.krull_dimension()
1

quo(I, names=None)¶

Create the quotient of R by the ideal I. This is a synonym for quotient()

EXAMPLES:

sage: R.<x,y> = PolynomialRing(QQ,2)
sage: S.<a,b> = R.quo((x^2, y))
sage: S
Quotient of Multivariate Polynomial Ring in x, y over Rational Field by the ideal (x^2, y)
sage: S.gens()
(a, 0)
sage: a == b
False

quotient(I, names=None)¶

Create the quotient of R by the ideal I.

INPUT:

R – a commutative ring
I – an ideal of R
names – (optional) names of the generators of the quotient (if there are multiple generators, you can specify a single character string and the generators are named in sequence starting with 0).

EXAMPLES:

sage: R.<x> = PolynomialRing(ZZ)
sage: I = R.ideal([4 + 3*x + x^2, 1 + x^2])
sage: S = R.quotient(I, 'a')
sage: S.gens()
(a,)

sage: R.<x,y> = PolynomialRing(QQ,2)
sage: S.<a,b> = R.quotient((x^2, y))
sage: S
Quotient of Multivariate Polynomial Ring in x, y over Rational Field by the ideal (x^2, y)
sage: S.gens()
(a, 0)
sage: a == b
False

quotient_ring(I, names=None)¶

Return the quotient of self by the ideal I of self. (Synonym for self.quotient(I).)

INPUT:

self – a ring R
I – an ideal of R
names – (optional) names of the generators of the quotient. (If there are multiple generators, you can specify a single character string and the generators are named in sequence starting with 0.)

OUTPUT:

R/I – the quotient ring of R by the ideal I

EXAMPLES:

sage: R.<x> = PolynomialRing(ZZ)
sage: I = R.ideal([4 + 3*x + x^2, 1 + x^2])
sage: S = R.quotient_ring(I, 'a')
sage: S.gens()
(a,)

sage: R.<x,y> = PolynomialRing(QQ,2)
sage: S.<a,b> = R.quotient_ring((x^2, y))
sage: S
Quotient of Multivariate Polynomial Ring in x, y over Rational Field by the ideal (x^2, y)
sage: S.gens()
(a, 0)
sage: a == b
False

class sage.rings.ring.DedekindDomain¶

Bases: sage.rings.ring.IntegralDomain

Generic Dedekind domain class.

A Dedekind domain is a Noetherian integral domain of Krull dimension one that is integrally closed in its field of fractions.

integral_closure()¶

Return self since Dedekind domains are integrally closed.

EXAMPLES:

sage: K = NumberField(x^2 + 1, 's')
sage: OK = K.ring_of_integers()
sage: OK.integral_closure()
Maximal Order in Number Field in s with defining polynomial x^2 + 1
sage: OK.integral_closure() == OK
True

sage: QQ.integral_closure() == QQ
True

is_integrally_closed()¶

Return True since Dedekind domains are integrally closed.

EXAMPLES:

The following are examples of Dedekind domains (Noetherian integral domains of Krull dimension one that are integrally closed over its field of fractions).

sage: ZZ.is_integrally_closed()
True
sage: K = NumberField(x^2 + 1, 's')
sage: OK = K.ring_of_integers()
sage: OK.is_integrally_closed()
True

These, however, are not Dedekind domains:

sage: QQ.is_integrally_closed()
True
sage: S = ZZ[sqrt(5)]; S.is_integrally_closed()
False
sage: T.<x,y> = PolynomialRing(QQ,2); T
Multivariate Polynomial Ring in x, y over Rational Field
sage: T.is_integral_domain()
True

is_noetherian()¶

Return True since Dedekind domains are Noetherian.

EXAMPLES:

The integers, $\ZZ$ , and rings of integers of number fields are Dedekind domains:

sage: ZZ.is_noetherian()
True
sage: K = NumberField(x^2 + 1, 's')
sage: OK = K.ring_of_integers()
sage: OK.is_noetherian()
True
sage: QQ.is_noetherian()
True

krull_dimension()¶

Return 1 since Dedekind domains have Krull dimension 1.

EXAMPLES:

The following are examples of Dedekind domains (Noetherian integral domains of Krull dimension one that are integrally closed over its field of fractions):

sage: ZZ.krull_dimension()
1
sage: K = NumberField(x^2 + 1, 's')
sage: OK = K.ring_of_integers()
sage: OK.krull_dimension()
1

The following are not Dedekind domains but have a krull_dimension function:

sage: QQ.krull_dimension()
0
sage: T.<x,y> = PolynomialRing(QQ,2); T
Multivariate Polynomial Ring in x, y over Rational Field
sage: T.krull_dimension()
2
sage: U.<x,y,z> = PolynomialRing(ZZ,3); U
Multivariate Polynomial Ring in x, y, z over Integer Ring
sage: U.krull_dimension()
4

sage: K.<i> = QuadraticField(-1)
sage: R = K.order(2*i); R
Order in Number Field in i with defining polynomial x^2 + 1
sage: R.is_maximal()
False
sage: R.krull_dimension()
1

class sage.rings.ring.EuclideanDomain¶

Bases: sage.rings.ring.PrincipalIdealDomain

Generic Euclidean domain class.

parameter()¶

Return an element of degree 1.

EXAMPLES:

sage: R.<x>=QQ[]
sage: R.parameter()
x

class sage.rings.ring.Field¶

Bases: sage.rings.ring.PrincipalIdealDomain

Generic field

algebraic_closure()¶

Return the algebraic closure of self.

Note

This is only implemented for certain classes of field.

EXAMPLES:

sage: K = PolynomialRing(QQ,'x').fraction_field(); K
Fraction Field of Univariate Polynomial Ring in x over Rational Field
sage: K.algebraic_closure()
...
NotImplementedError: Algebraic closures of general fields not implemented.

category()¶

Return the category of this field, which is the category of fields.

EXAMPLES:

Examples with fields:

sage: QQ.category()
Category of fields
sage: RR.category()
Category of fields
sage: CC.category()
Category of fields
sage: R.<x> = PolynomialRing(ZZ)
sage: Q = R.fraction_field()
sage: Q.category()
Category of fields

Although fields themselves, number fields belong to the category of ‘number fields’:

sage: F = NumberField(x^2 + 1, 'i')
sage: F.category()
Category of number fields

divides(x, y, coerce=True)¶

Return True if x divides y in this field (usually True in a field!). If coerce is True (the default), first coerce x and y into self.

EXAMPLES:

sage: QQ.divides(2, 3/4)
True
sage: QQ.divides(0, 5)
False

fraction_field()¶

Return the fraction field of self.

EXAMPLES:

Since fields are their own field of fractions, we simply get the original field in return:

sage: QQ.fraction_field()
Rational Field
sage: RR.fraction_field()
Real Field with 53 bits of precision
sage: CC.fraction_field()
Complex Field with 53 bits of precision

sage: F = NumberField(x^2 + 1, 'i')
sage: F.fraction_field()
Number Field in i with defining polynomial x^2 + 1

ideal(*gens, **kwds)¶

Return the ideal generated by gens.

EXAMPLES:

sage: QQ.ideal(2)
Principal ideal (1) of Rational Field
sage: QQ.ideal(0)
Principal ideal (0) of Rational Field

integral_closure()¶

Return this field, since fields are integrally closed in their fraction field.

EXAMPLES:

sage: QQ.integral_closure()
Rational Field
sage: Frac(ZZ['x,y']).integral_closure()
Fraction Field of Multivariate Polynomial Ring in x, y over Integer Ring

is_field(proof=True)¶

Return True since this is a field.

EXAMPLES:

sage: Frac(ZZ['x,y']).is_field()
True

is_integrally_closed()¶

Return True since fields are trivially integrally closed in their fraction field (since they are their own fraction field).

EXAMPLES:

sage: Frac(ZZ['x,y']).is_integrally_closed()
True

is_noetherian()¶

Return True since fields are Noetherian rings.

EXAMPLES:

sage: QQ.is_noetherian()
True

krull_dimension()¶

Return the Krull dimension of this field, which is 0.

EXAMPLES:

sage: QQ.krull_dimension()
0
sage: Frac(QQ['x,y']).krull_dimension()
0

prime_subfield()¶

Return the prime subfield of self.

EXAMPLES:

sage: k = GF(9, 'a')
sage: k.prime_subfield()
Finite Field of size 3

class sage.rings.ring.IntegralDomain¶

Bases: sage.rings.ring.CommutativeRing

Generic integral domain class.

is_field(proof=True)¶

Return True if this ring is a field.

EXAMPLES:

sage: GF(7).is_field()
True

The following examples have their own is_field implementations:

sage: ZZ.is_field(); QQ.is_field()
False
True
sage: R.<x> = PolynomialRing(QQ); R.is_field()
False

An example where we raise a NotImplementedError:

sage: R = IntegralDomain(ZZ)
sage: R.is_field()
...
NotImplementedError

is_integral_domain(proof=True)¶

Return True, since this ring is an integral domain.

(This is a naive implementation for objects with type IntegralDomain)

EXAMPLES:

sage: ZZ.is_integral_domain(); QQ.is_integral_domain(); ZZ[x].is_integral_domain()
True
True
True
sage: R = ZZ.quotient(ZZ.ideal(10)); R.is_integral_domain()
False

is_integrally_closed()¶

Return True if this ring is integrally closed in its field of fractions; otherwise return False.

When no algorithm is implemented for this, then this function raises a NotImplementedError.

Note that is_integrally_closed has a naive implementation in fields. For every field 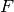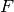$F$ , $F$ is its own field of fractions, hence every element of 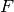$F$ is integral over $F$ .

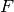EXAMPLES:

sage: ZZ.is_integrally_closed()
True
sage: QQ.is_integrally_closed()
True
sage: QQbar.is_integrally_closed()
True
sage: Z5 = Integers(5); Z5
Ring of integers modulo 5
sage: Z5.is_integrally_closed()
...
AttributeError: 'IntegerModRing_generic' object has no attribute 'is_integrally_closed'

class sage.rings.ring.NoetherianRing¶

Bases: sage.rings.ring.CommutativeRing

Generic Noetherian ring class.

A Noetherian ring is a commutative ring in which every ideal is finitely generated.

At present this is not actually used anywhere in the Sage code base (largely because of the lack of multiple inheritance for Cython classes).

is_noetherian()¶

Return True since this ring is Noetherian.

EXAMPLES:

sage: ZZ.is_noetherian()
True
sage: QQ.is_noetherian()
True
sage: R.<x> = PolynomialRing(QQ)
sage: R.is_noetherian()
True

class sage.rings.ring.PrincipalIdealDomain¶

Bases: sage.rings.ring.IntegralDomain

Generic principal ideal domain.

class_group()¶

Return the trivial group, since the class group of a PID is trivial.

EXAMPLES:

sage: QQ.class_group()
Trivial Abelian Group

content(x, y, coerce=True)¶

Return the content of x and y, i.e. the unique element c of self such that x/c and y/c are coprime and integral.

EXAMPLES:

sage: QQ.content(ZZ(42), ZZ(48)); type(QQ.content(ZZ(42), ZZ(48)))
6
<type 'sage.rings.rational.Rational'>
sage: QQ.content(1/2, 1/3)
1/6
sage: factor(1/2); factor(1/3); factor(1/6)
2^-1
3^-1
2^-1 * 3^-1
sage: a = (2*3)/(7*11); b = (13*17)/(19*23)
sage: factor(a); factor(b); factor(QQ.content(a,b))
2 * 3 * 7^-1 * 11^-1
13 * 17 * 19^-1 * 23^-1
7^-1 * 11^-1 * 19^-1 * 23^-1

Note the changes to the second entry:

sage: c = (2*3)/(7*11); d = (13*17)/(7*19*23)
sage: factor(c); factor(d); factor(QQ.content(c,d))
2 * 3 * 7^-1 * 11^-1
7^-1 * 13 * 17 * 19^-1 * 23^-1
7^-1 * 11^-1 * 19^-1 * 23^-1
sage: e = (2*3)/(7*11); f = (13*17)/(7^3*19*23)
sage: factor(e); factor(f); factor(QQ.content(e,f))
2 * 3 * 7^-1 * 11^-1
7^-3 * 13 * 17 * 19^-1 * 23^-1
7^-3 * 11^-1 * 19^-1 * 23^-1

gcd(x, y, coerce=True)¶

Return the greatest common divisor of x and y, as elements of self.

EXAMPLES:

The integers are a principal ideal domain and hence a GCD domain:

sage: ZZ.gcd(42, 48)
6
sage: 42.factor(); 48.factor()
2 * 3 * 7
2^4 * 3
sage: ZZ.gcd(2^4*7^2*11, 2^3*11*13)
88
sage: 88.factor()
2^3 * 11

In a field, any nonzero element is a GCD of any nonempty set of elements. For concreteness, Sage returns 1 in these cases:

sage: QQ.gcd(ZZ(42), ZZ(48)); type(QQ.gcd(ZZ(42), ZZ(48)))
1
<type 'sage.rings.rational.Rational'>
sage: QQ.gcd(1/2, 1/3)
1

Polynomial rings over fields are GCD domains as well. Here is a simple example over the ring of polynomials over the rationals as well as over an extension ring. Note that gcd requires x and y to be coercible:

sage: R.<x> = PolynomialRing(QQ)
sage: S.<a> = NumberField(x^2 - 2, 'a')
sage: f = (x - a)*(x + a); g = (x - a)*(x^2 - 2)
sage: print f; print g
x^2 - 2
x^3 - a*x^2 - 2*x + 2*a
sage: f in R
True
sage: g in R
False
sage: R.gcd(f,g)
...
TypeError: Unable to coerce 2*a to a rational
sage: R.base_extend(S).gcd(f,g)
x^2 - 2
sage: R.base_extend(S).gcd(f, (x - a)*(x^2 - 3))
x - a

is_noetherian()¶

Every principal ideal domain is noetherian, so we return True.

EXAMPLES:

sage: Zp(5).is_noetherian()
True

class sage.rings.ring.Ring¶

Bases: sage.structure.parent_gens.ParentWithGens

Generic ring class.

base_extend(R)¶

EXAMPLES:

sage: QQ.base_extend(GF(7))
...
TypeError: no base extension defined
sage: ZZ.base_extend(GF(7))
Finite Field of size 7

category()¶

Return the category to which this ring belongs.

EXAMPLES:

sage: FreeAlgebra(QQ, 3, 'x').category() # todo: use a ring which is not an algebra!
Category of rings

characteristic()¶

Return the characteristic of this ring.

EXAMPLES:

sage: QQ.characteristic()
0
sage: GF(19).characteristic()
19
sage: Integers(8).characteristic()
8
sage: Zp(5).characteristic()
0

ideal(*x, **kwds)¶

Return the ideal defined by x, i.e., generated by x.

INPUT:

*x – list or tuple of generators (or several input arguments)
coerce – bool (default: True); this must be a keyword argument. Only set it to False if you are certain that each generator is already in the ring.

TODO: For noncommutative rings, distinguish between ideals, right ideals, and left ideals.

EXAMPLES:

sage: R.<x,y> = QQ[]
sage: R.ideal(x,y)
Ideal (x, y) of Multivariate Polynomial Ring in x, y over Rational Field
sage: R.ideal(x+y^2)
Ideal (y^2 + x) of Multivariate Polynomial Ring in x, y over Rational Field
sage: R.ideal( [x^3,y^3+x^3] )
Ideal (x^3, x^3 + y^3) of Multivariate Polynomial Ring in x, y over Rational Field

is_atomic_repr()¶

True if the elements have atomic string representations, in the sense that they print if they print at s, then -s means the negative of s. For example, integers are atomic but polynomials are not.

EXAMPLES:

sage: Zp(7).is_atomic_repr()
False
sage: QQ.is_atomic_repr()
True
sage: CDF.is_atomic_repr()
False

is_commutative()¶

Return True if this ring is commutative.

EXAMPLES:

sage: QQ.is_commutative()
True
sage: QQ['x,y,z'].is_commutative()
True
sage: Q.<i,j,k> = QuaternionAlgebra(QQ, -1,-1)
sage: Q.is_commutative()
False

is_exact()¶

Return True if elements of this ring are represented exactly, i.e., there is no precision loss when doing arithmetic.

Note

This defaults to True, so even if it does return True you have no guarantee (unless the ring has properly overloaded this).

EXAMPLES:

sage: QQ.is_exact()
True
sage: ZZ.is_exact()
True
sage: Qp(7).is_exact()
False
sage: Zp(7, type='capped-abs').is_exact()
False

is_field(proof=True)¶

Return True if this ring is a field.

INPUT:

proof - Determines what to do in unknown cases (default: True)

ALGORITHM:

If the parameter proof is set to True, the returned value is correct but the method might throw an error. Otherwise, if it is set to False, the method returns True if it can establish that self is a field and False otherwise.

EXAMPLES:

sage: QQ.is_field()
True
sage: GF(9,'a').is_field()
True
sage: ZZ.is_field()
False
sage: QQ['x'].is_field()
False
sage: Frac(QQ['x']).is_field()
True

This illustrates the use of the proof parameter:

sage: R.<a,b> = QQ[]
sage: S.<x,y> = R.quo((b^3))
sage: S.is_field(proof = True)
...
NotImplementedError
sage: S.is_field(proof = False)
False

is_finite()¶

Return True if this ring is finite.

EXAMPLES:

sage: QQ.is_finite()
False
sage: GF(2^10,'a').is_finite()
True
sage: R.<x> = GF(7)[]
sage: R.is_finite()
False
sage: S.<y> = R.quo(x^2+1)
sage: S.is_finite()
True        

is_integral_domain(proof=True)¶

Return True if this ring is an integral domain.

INPUT:

proof - Determines what to do in unknown cases (default: True)

ALGORITHM:

If the parameter proof is set to True, the returned value is correct but the method might throw an error. Otherwise, if it is set to False, the method returns True if it can establish that self is an integral domain and False otherwise.

EXAMPLES:

sage: QQ.is_integral_domain()
True
sage: ZZ.is_integral_domain()
True
sage: ZZ['x,y,z'].is_integral_domain()
True
sage: Integers(8).is_integral_domain()
False
sage: Zp(7).is_integral_domain()
True
sage: Qp(7).is_integral_domain()
True
sage: R.<a,b> = QQ[]
sage: S.<x,y> = R.quo((b^3))
sage: S.is_integral_domain()
False

This illustrates the use of the proof parameter:

sage: R.<a,b> = ZZ[]
sage: S.<x,y> = R.quo((b^3))
sage: S.is_integral_domain(proof = True)
...
NotImplementedError
sage: S.is_integral_domain(proof = False)
False

is_noetherian()¶

Return True if this ring is Noetherian.

EXAMPLES:

sage: QQ.is_noetherian()
True
sage: ZZ.is_noetherian()
True

is_prime_field()¶

Return True if this ring is one of the prime fields $\QQ$ or $\GF{p}$ .

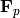EXAMPLES:

sage: QQ.is_prime_field()
True
sage: GF(3).is_prime_field()
True
sage: GF(9,'a').is_prime_field()
False
sage: ZZ.is_prime_field()
False
sage: QQ['x'].is_prime_field()
False
sage: Qp(19).is_prime_field()
False

is_ring()¶

Return True since self is a ring.

EXAMPLES:

sage: QQ.is_ring()
True

is_subring(other)¶

Return True if the canonical map from self to other is injective.

Raises a NotImplementedError if not known.

EXAMPLES:

sage: ZZ.is_subring(QQ)
True
sage: ZZ.is_subring(GF(19))
False

is_zero()¶

True if this is the zero ring.

EXAMPLES:

sage: Integers(1).is_zero()
True
sage: Integers(2).is_zero()
False
sage: QQ.is_zero()
False
sage: R.<x> = ZZ[]
sage: R.quo(1).is_zero()
True  
sage: R.<x> = GF(101)[]
sage: R.quo(77).is_zero()
True
sage: R.quo(x^2+1).is_zero()
False

one()¶

Return the one element of this ring (cached), if it exists.

EXAMPLES:

sage: ZZ.one_element()
1
sage: QQ.one_element()
1
sage: QQ['x'].one_element()
1

The result is cached:

sage: ZZ.one_element() is ZZ.one_element()
True

one_element()¶

Return the one element of this ring (cached), if it exists.

EXAMPLES:

sage: ZZ.one_element()
1
sage: QQ.one_element()
1
sage: QQ['x'].one_element()
1

The result is cached:

sage: ZZ.one_element() is ZZ.one_element()
True

order()¶

The number of elements of self.

EXAMPLES:

sage: GF(19).order()
19
sage: QQ.order()
+Infinity

principal_ideal(gen, coerce=True)¶

Return the principal ideal generated by gen.

EXAMPLES:

sage: R.<x,y> = ZZ[]
sage: R.principal_ideal(x+2*y)
Ideal (x + 2*y) of Multivariate Polynomial Ring in x, y over Integer Ring

random_element(bound=2)¶

Return a random integer coerced into this ring, where the integer is chosen uniformly from the interval [-bound,bound].

INPUT:

bound – integer (default: 2)

ALGORITHM:

Uses Python’s randint.

TESTS:

The following example returns a NotImplementedError since the generic ring class __call__ function returns a NotImplementedError. Note that sage.rings.ring.Ring.random_element performs a call in the generic ring class by a random integer:

sage: R = sage.rings.ring.Ring(ZZ); R
<type 'sage.rings.ring.Ring'>
sage: R.random_element()
...
NotImplementedError

unit_ideal()¶

Return the unit ideal of this ring.

EXAMPLES:

sage: Zp(7).unit_ideal()
Principal ideal (1 + O(7^20)) of 7-adic Ring with capped relative precision 20

zero()¶

Return the zero element of this ring (cached).

EXAMPLES:

sage: ZZ.zero_element()
0
sage: QQ.zero_element()
0
sage: QQ['x'].zero_element()
0

The result is cached:

sage: ZZ.zero_element() is ZZ.zero_element()
True

zero_element()¶

Return the zero element of this ring (cached).

EXAMPLES:

sage: ZZ.zero_element()
0
sage: QQ.zero_element()
0
sage: QQ['x'].zero_element()
0

The result is cached:

sage: ZZ.zero_element() is ZZ.zero_element()
True

zero_ideal()¶

Return the zero ideal of this ring (cached).

EXAMPLES:

sage: ZZ.zero_ideal()
Principal ideal (0) of Integer Ring
sage: QQ.zero_ideal()
Principal ideal (0) of Rational Field
sage: QQ['x'].zero_ideal()
Principal ideal (0) of Univariate Polynomial Ring in x over Rational Field

The result is cached:

sage: ZZ.zero_ideal() is ZZ.zero_ideal()
True

zeta(n=2, all=False)¶

Return an n-th root of unity in self if there is one, or raise an ArithmeticError otherwise.

INPUT:

n – positive integer
all – bool, default: False. If True, return a list of all n-th roots of 1.

OUTPUT:

element of self of finite order

EXAMPLES:

sage: QQ.zeta()
-1
sage: QQ.zeta(1)
1
sage: CyclotomicField(6).zeta()
zeta6
sage: CyclotomicField(3).zeta()
zeta3
sage: CyclotomicField(3).zeta().multiplicative_order()
3
sage: a = GF(7).zeta(); a
3
sage: a.multiplicative_order()
6
sage: a = GF(49,'z').zeta(); a
z
sage: a.multiplicative_order()
48
sage: a = GF(49,'z').zeta(2); a
6
sage: a.multiplicative_order()
2
sage: QQ.zeta(3)
...
ValueError: no n-th root of unity in rational field
sage: Zp(7, prec=8).zeta()
3 + 4*7 + 6*7^2 + 3*7^3 + 2*7^5 + 6*7^6 + 2*7^7 + O(7^8)

zeta_order()¶

Return the order of the distinguished root of unity in self.

EXAMPLES:

sage: CyclotomicField(19).zeta_order()
38
sage: GF(19).zeta_order()
18
sage: GF(5^3,'a').zeta_order()
124
sage: Zp(7, prec=8).zeta_order()
6

sage.rings.ring.gen_name(x, name_chr)¶

Used to find a name for a generator when rings are created using the __getitem__ syntax, e.g. ZZ['x']. If x is a symbolic variable, return the name of x; if x is the symbolic square root of a positive integer d, return “sqrtd”; else, return a letter of the alphabet and increment a counter to avoid that letter being used again.

EXAMPLES:

sage: from sage.rings.ring import gen_name
sage: gen_name(sqrt(5), 1)
('sqrt5', 1)
sage: gen_name(sqrt(-17), 88)
('X', 89)
sage: gen_name(x, 1)
('x', 1)

sage.rings.ring.is_Field(x)¶

Return True if x is a field.

EXAMPLES:

sage: from sage.rings.ring import is_Field
sage: is_Field(QQ)
True
sage: is_Field(ZZ)
False
sage: is_Field(pAdicField(2))
True
sage: is_Field(5)
False

sage.rings.ring.is_Ring(x)¶

Return True if x is a ring.

EXAMPLES:

sage: from sage.rings.ring import is_Ring
sage: is_Ring(ZZ)
True

Rings¶

Previous topic

Next topic

This Page

Navigation

Rings¶

Previous topic

Next topic

This Page

Quick search

Navigation