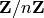 , implemented using NTL.¶
, implemented using NTL.¶This implementation is generally slower than the FLINT implementation in
polynomial_zmod_flint, so we use FLINT by
default when the modulus is small enough; but NTL does not require that  be
int-sized, so we use it as default when
be
int-sized, so we use it as default when  is too large for FLINT.
is too large for FLINT.
Note that the classes Polynomial_dense_modn_ntl_zz and Polynomial_dense_modn_ntl_ZZ are different; the former is limited to moduli less than a certain bound, while the latter supports arbitrarily large moduli.
AUTHORS:
Bases: sage.rings.polynomial.polynomial_element.Polynomial
A dense polynomial over the integers modulo n, where n is composite, with the underlying arithmetic done using NTL.
EXAMPLES:
sage: R.<x> = PolynomialRing(Integers(16))
sage: f = x^3 - x + 17
sage: f^2
x^6 + 14*x^4 + 2*x^3 + x^2 + 14*x + 1
sage: loads(f.dumps()) == f
True
sage: R.<x> = Integers(100)[]
sage: p = 3*x
sage: q = 7*x
sage: p+q
10*x
sage: R.<x> = Integers(8)[]
sage: parent(p)
Univariate Polynomial Ring in x over Ring of integers modulo 100
sage: p + q
10*x
sage: R({10:-1})
7*x^10
Return a new copy of the list of the underlying elements of self.
EXAMPLES:
sage: _.<x> = Integers(100)[]
sage: f = x^3 + 3*x - 17
sage: f.list()
[83, 3, 0, 1]
Return underlying NTL representation of this polynomial. Additional ‘’bonus’’ functionality is available through this function.
Warning
You must call ntl.set_modulus(ntl.ZZ(n)) before doing arithmetic with this object!
Set the value of this polynomial directly from a vector or string.
Polynomials over the integers modulo n are stored internally using NTL’s ZZ_pX class. Use this function to set the value of this polynomial using the NTL constructor, which is potentially very fast. The input v is either a vector of ints or a string of the form [ n1 n2 n3 ... ] where the ni are integers and there are no commas between them. The optimal input format is the string format, since that’s what NTL uses by default.
EXAMPLES:
sage: R.<x> = PolynomialRing(Integers(100))
sage: from sage.rings.polynomial.polynomial_modn_dense_ntl import Polynomial_dense_mod_n as poly_modn_dense
sage: poly_modn_dense(R, ([1,-2,3]))
3*x^2 + 98*x + 1
sage: f = poly_modn_dense(R, 0)
sage: f.ntl_set_directly([1,-2,3])
sage: f
3*x^2 + 98*x + 1
sage: f.ntl_set_directly('[1 -2 3 4]')
sage: f
4*x^3 + 3*x^2 + 98*x + 1
A decorator to be used on binary operation methods that should operate on elements of the same parent. If the parents of the arguments differ, coercion is performed, then the method is re-looked up by name on the first argument.
In short, using the NamedBinopMethod (alias coerce_binop) decorator on a method gives it the exact same semantics of the basic arithmetic operations like _add_, _sub_, etc. in that both operands are guaranteed to have exactly the same parent.
Returns this polynomial multiplied by the power 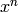 . If
. If  is negative,
terms below
is negative,
terms below 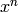 will be discarded. Does not change this polynomial.
will be discarded. Does not change this polynomial.
EXAMPLES:
sage: R.<x> = PolynomialRing(Integers(12345678901234567890))
sage: p = x^2 + 2*x + 4
sage: p.shift(0)
x^2 + 2*x + 4
sage: p.shift(-1)
x + 2
sage: p.shift(-5)
0
sage: p.shift(2)
x^4 + 2*x^3 + 4*x^2
TESTS:
sage: p = R(0)
sage: p.shift(3).is_zero()
True
sage: p.shift(-3).is_zero()
True
AUTHOR:
See sage.rings.polynomial.polynomial_modn_dense_ntl.small_roots() for the documentation of this function.
EXAMPLE:
sage: N = 10001
sage: K = Zmod(10001)
sage: P.<x> = PolynomialRing(K)
sage: f = x^3 + 10*x^2 + 5000*x - 222
sage: f.small_roots()
[4]
Bases: sage.rings.polynomial.polynomial_modn_dense_ntl.Polynomial_dense_mod_n
A dense polynomial over the integers modulo p, where p is prime.
EXAMPLES:
sage: _.<x> = PolynomialRing(GF(19))
sage: f = x^3 + 3*x - 17
sage: f.discriminant()
12
A decorator to be used on binary operation methods that should operate on elements of the same parent. If the parents of the arguments differ, coercion is performed, then the method is re-looked up by name on the first argument.
In short, using the NamedBinopMethod (alias coerce_binop) decorator on a method gives it the exact same semantics of the basic arithmetic operations like _add_, _sub_, etc. in that both operands are guaranteed to have exactly the same parent.
A decorator to be used on binary operation methods that should operate on elements of the same parent. If the parents of the arguments differ, coercion is performed, then the method is re-looked up by name on the first argument.
In short, using the NamedBinopMethod (alias coerce_binop) decorator on a method gives it the exact same semantics of the basic arithmetic operations like _add_, _sub_, etc. in that both operands are guaranteed to have exactly the same parent.
A decorator to be used on binary operation methods that should operate on elements of the same parent. If the parents of the arguments differ, coercion is performed, then the method is re-looked up by name on the first argument.
In short, using the NamedBinopMethod (alias coerce_binop) decorator on a method gives it the exact same semantics of the basic arithmetic operations like _add_, _sub_, etc. in that both operands are guaranteed to have exactly the same parent.
Bases: sage.rings.polynomial.polynomial_modn_dense_ntl.Polynomial_dense_mod_n
EXAMPLES:
sage: R.<x> = Integers(14^34)[]
sage: f = x^4 - x - 1
sage: f.degree()
4
sage: f = 14^43*x + 1
sage: f.degree()
0
A decorator to be used on binary operation methods that should operate on elements of the same parent. If the parents of the arguments differ, coercion is performed, then the method is re-looked up by name on the first argument.
In short, using the NamedBinopMethod (alias coerce_binop) decorator on a method gives it the exact same semantics of the basic arithmetic operations like _add_, _sub_, etc. in that both operands are guaranteed to have exactly the same parent.
Reverses the coefficients of self. The reverse of 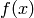 is
is 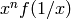 .
.
The degree will go down if the constant term is zero.
EXAMPLES:
sage: R.<x> = Integers(12^29)[]
sage: f = x^4 + 2*x + 5
sage: f.reverse()
5*x^4 + 2*x^3 + 1
sage: f = x^3 + x
sage: f.reverse()
x^2 + 1
Shift self to left by  , which is multiplication by
, which is multiplication by 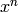 ,
truncating if
,
truncating if  is negative.
is negative.
EXAMPLES:
sage: R.<x> = Integers(12^30)[]
sage: f = x^7 + x + 1
sage: f.shift(1)
x^8 + x^2 + x
sage: f.shift(-1)
x^6 + 1
sage: f.shift(10).shift(-10) == f
True
TESTS:
sage: p = R(0)
sage: p.shift(3).is_zero()
True
sage: p.shift(-3).is_zero()
True
Returns this polynomial mod 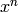 .
.
EXAMPLES:
sage: R.<x> = Integers(15^30)[]
sage: f = sum(x^n for n in range(10)); f
x^9 + x^8 + x^7 + x^6 + x^5 + x^4 + x^3 + x^2 + x + 1
sage: f.truncate(6)
x^5 + x^4 + x^3 + x^2 + x + 1
Returns the valuation of self, that is, the power of the lowest non-zero monomial of self.
EXAMPLES:
sage: R.<x> = Integers(10^50)[]
sage: x.valuation()
1
sage: f = x-3; f.valuation()
0
sage: f = x^99; f.valuation()
99
sage: f = x-x; f.valuation()
+Infinity
Bases: sage.rings.polynomial.polynomial_modn_dense_ntl.Polynomial_dense_mod_n
EXAMPLES:
sage: R.<x> = Integers(77)[]
sage: f = x^4 - x - 1
sage: f.degree()
4
sage: f = 77*x + 1
sage: f.degree()
0
Returns the coefficients of self as efficiently as possible as a list of python ints.
EXAMPLES:
sage: R.<x> = Integers(100)[]
sage: from sage.rings.polynomial.polynomial_modn_dense_ntl import Polynomial_dense_mod_n as poly_modn_dense
sage: f = poly_modn_dense(R,[5,0,0,1])
sage: f.int_list()
[5, 0, 0, 1]
sage: [type(a) for a in f.int_list()]
[<type 'int'>, <type 'int'>, <type 'int'>, <type 'int'>]
A decorator to be used on binary operation methods that should operate on elements of the same parent. If the parents of the arguments differ, coercion is performed, then the method is re-looked up by name on the first argument.
In short, using the NamedBinopMethod (alias coerce_binop) decorator on a method gives it the exact same semantics of the basic arithmetic operations like _add_, _sub_, etc. in that both operands are guaranteed to have exactly the same parent.
Reverses the coefficients of self. The reverse of 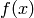 is
is 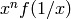 .
.
The degree will go down if the constant term is zero.
EXAMPLES:
sage: R.<x> = Integers(77)[]
sage: f = x^4 - x - 1
sage: f.reverse()
76*x^4 + 76*x^3 + 1
sage: f = x^3 - x
sage: f.reverse()
76*x^2 + 1
Shift self to left by  , which is multiplication by
, which is multiplication by 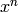 ,
truncating if
,
truncating if  is negative.
is negative.
EXAMPLES:
sage: R.<x> = Integers(77)[]
sage: f = x^7 + x + 1
sage: f.shift(1)
x^8 + x^2 + x
sage: f.shift(-1)
x^6 + 1
sage: f.shift(10).shift(-10) == f
True
TESTS:
sage: p = R(0)
sage: p.shift(3).is_zero()
True
sage: p.shift(-3).is_zero()
True
Returns this polynomial mod 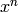 .
.
EXAMPLES:
sage: R.<x> = Integers(77)[]
sage: f = sum(x^n for n in range(10)); f
x^9 + x^8 + x^7 + x^6 + x^5 + x^4 + x^3 + x^2 + x + 1
sage: f.truncate(6)
x^5 + x^4 + x^3 + x^2 + x + 1
Returns the valuation of self, that is, the power of the lowest non-zero monomial of self.
EXAMPLES:
sage: R.<x> = Integers(10)[]
sage: x.valuation()
1
sage: f = x-3; f.valuation()
0
sage: f = x^99; f.valuation()
99
sage: f = x-x; f.valuation()
+Infinity
Let  be the characteristic of the base ring this polynomial
is defined over: N = self.base_ring().characteristic().
This method returns small roots of this polynomial modulo some
factor
be the characteristic of the base ring this polynomial
is defined over: N = self.base_ring().characteristic().
This method returns small roots of this polynomial modulo some
factor 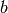 of
of  with the constraint that
with the constraint that 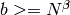 .
Small in this context means that if
.
Small in this context means that if  is a root of
is a root of 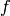 modulo
modulo 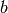 then
then 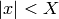 . This
. This  is either provided by the
user or the maximum
is either provided by the
user or the maximum  is chosen such that this algorithm
terminates in polynomial time. If
is chosen such that this algorithm
terminates in polynomial time. If  is chosen automatically
it is
is chosen automatically
it is  .
The algorithm may also return some roots which are larger than
.
The algorithm may also return some roots which are larger than  .
‘This algorithm’ in this context means Coppersmith’s algorithm for finding
small roots using the LLL algorithm. The implementation of this algorithm
follows Alexander May’s PhD thesis referenced below.
.
‘This algorithm’ in this context means Coppersmith’s algorithm for finding
small roots using the LLL algorithm. The implementation of this algorithm
follows Alexander May’s PhD thesis referenced below.
INPUT:
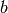 where
where 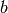 is a factor of
is a factor of  and
and 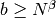 . (Default: 1.0, so
. (Default: 1.0, so 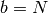 .)
.) described above. (Default:
described above. (Default: 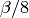 )
)EXAMPLES:
First consider a small example:
sage: N = 10001
sage: K = Zmod(10001)
sage: P.<x> = PolynomialRing(K)
sage: f = x^3 + 10*x^2 + 5000*x - 222
This polynomial has no roots without modular reduction (i.e. over  ):
):
sage: f.change_ring(ZZ).roots()
[]
To compute its roots we need to factor the modulus  and use the Chinese
remainder theorem:
and use the Chinese
remainder theorem:
sage: p,q = N.prime_divisors()
sage: f.change_ring(GF(p)).roots()
[(4, 1)]
sage: f.change_ring(GF(q)).roots()
[(4, 1)]
sage: crt(4, 4, p, q)
4
This root is quite small compared to  , so we can attempt to
recover it without factoring
, so we can attempt to
recover it without factoring  using Coppersmith’s small root
method:
using Coppersmith’s small root
method:
sage: f.small_roots()
[4]
An application of this method is to consider RSA. We are using 512-bit RSA
with public exponent 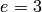 to encrypt a 56-bit DES key. Because it would be
easy to attack this setting if no padding was used we pad the key
to encrypt a 56-bit DES key. Because it would be
easy to attack this setting if no padding was used we pad the key  with
1s to get a large number:
with
1s to get a large number:
sage: Nbits, Kbits = 512, 56
sage: e = 3
We choose two primes of size 256-bit each:
sage: p = 2^256 + 2^8 + 2^5 + 2^3 + 1
sage: q = 2^256 + 2^8 + 2^5 + 2^3 + 2^2 + 1
sage: N = p*q
sage: ZmodN = Zmod( N )
We choose a random key:
sage: K = ZZ.random_element(0, 2^Kbits)
and pad it with 512-56=456 1s:
sage: Kdigits = K.digits(2)
sage: M = [0]*Kbits + [1]*(Nbits-Kbits)
sage: for i in range(len(Kdigits)): M[i] = Kdigits[i]
sage: M = ZZ(M, 2)
Now we encrypt the resulting message:
sage: C = ZmodN(M)^e
To recover  we consider the following polynomial modulo
we consider the following polynomial modulo  :
:
sage: P.<x> = PolynomialRing(ZmodN)
sage: f = (2^Nbits - 2^Kbits + x)^e - C
and recover its small roots:
sage: Kbar = f.small_roots()[0]
sage: K == Kbar
True
The same algorithm can be used to factor 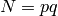 if partial
knowledge about
if partial
knowledge about 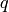 is available. This example is from the
Magma handbook:
is available. This example is from the
Magma handbook:
First, we set up  ,
, 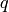 and
and  :
:
sage: length = 512
sage: hidden = 110
sage: p = next_prime(2^int(round(length/2)))
sage: q = next_prime( round(pi.n()*p) )
sage: N = p*q
Now we disturb the low 110 bits of 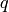 :
:
sage: qbar = q + ZZ.random_element(0,2^hidden-1)
And try to recover 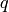 from it:
from it:
sage: F.<x> = PolynomialRing(Zmod(N))
sage: f = x - qbar
We know that the error is 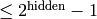 and that the modulus
we are looking for is
and that the modulus
we are looking for is 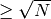 :
:
sage: set_verbose(2)
sage: d = f.small_roots(X=2^hidden-1, beta=0.5)[0] # time random
verbose 2 (<module>) m = 4
verbose 2 (<module>) t = 4
verbose 2 (<module>) X = 1298074214633706907132624082305023
verbose 1 (<module>) LLL of 8x8 matrix (algorithm fpLLL:wrapper)
verbose 1 (<module>) LLL finished (time = 0.006998)
sage: q == qbar - d
True
REFERENCES:
Don Coppersmith. Finding a small root of a univariate modular equation. In Advances in Cryptology, EuroCrypt 1996, volume 1070 of Lecture Notes in Computer Science, p. 155–165. Springer, 1996. http://cr.yp.to/bib/2001/coppersmith.pdf
Alexander May. New RSA Vulnerabilities Using Lattice Reduction Methods. PhD thesis, University of Paderborn, 2003. http://www.informatik.tu-darmstadt.de/KP/publications/03/bp.ps