Dense univariate polynomials over , implemented using MPFR

class sage.rings.polynomial.polynomial_real_mpfr_dense.PolynomialRealDense

Bases: sage.rings.polynomial.polynomial_element.Polynomial

change_ring(R)

EXAMPLES:

sage: from sage.rings.polynomial.polynomial_real_mpfr_dense import PolynomialRealDense
sage: f = PolynomialRealDense(RR['x'], [-2, 0, 1.5])
sage: f.change_ring(QQ)
3/2*x^2 - 2
sage: f.change_ring(RealField(10))
1.5*x^2 - 2.0
sage: f.change_ring(RealField(100))
1.5000000000000000000000000000*x^2 - 2.0000000000000000000000000000

degree()

EXAMPLES:

sage: from sage.rings.polynomial.polynomial_real_mpfr_dense import PolynomialRealDense
sage: f = PolynomialRealDense(RR['x'], [1, 2, 3]); f
3.00000000000000*x^2 + 2.00000000000000*x + 1.00000000000000
sage: f.degree()
2

gcd(other)

A decorator to be used on binary operation methods that should operate on elements of the same parent. If the parents of the arguments differ, coercion is performed, then the method is re-looked up by name on the first argument.

In short, using the NamedBinopMethod (alias coerce_binop) decorator on a method gives it the exact same semantics of the basic arithmetic operations like _add_, _sub_, etc. in that both operands are guaranteed to have exactly the same parent.

integral()

EXAMPLES:

sage: from sage.rings.polynomial.polynomial_real_mpfr_dense import PolynomialRealDense
sage: f = PolynomialRealDense(RR['x'], [3, pi, 1])
sage: f.integral()
0.333333333333333*x^3 + 1.57079632679490*x^2 + 3.00000000000000*x

list()

EXAMPLES:

sage: from sage.rings.polynomial.polynomial_real_mpfr_dense import PolynomialRealDense
sage: f = PolynomialRealDense(RR['x'], [1, 0, -2]); f
-2.00000000000000*x^2 + 1.00000000000000
sage: f.list()
[1.00000000000000, 0.000000000000000, -2.00000000000000]

quo_rem(other)

A decorator to be used on binary operation methods that should operate on elements of the same parent. If the parents of the arguments differ, coercion is performed, then the method is re-looked up by name on the first argument.

In short, using the NamedBinopMethod (alias coerce_binop) decorator on a method gives it the exact same semantics of the basic arithmetic operations like _add_, _sub_, etc. in that both operands are guaranteed to have exactly the same parent.

reverse()

Returns 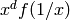where is the degree of .

EXAMPLES:

sage: from sage.rings.polynomial.polynomial_real_mpfr_dense import PolynomialRealDense
sage: f = PolynomialRealDense(RR['x'], [-3, pi, 0, 1])
sage: f.reverse()
-3.00000000000000*x^3 + 3.14159265358979*x^2 + 1.00000000000000

shift(n)

Returns this polynomial multiplied by the power 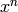. If is negative, terms below 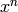will be discarded. Does not change this polynomial.

EXAMPLES:

sage: from sage.rings.polynomial.polynomial_real_mpfr_dense import PolynomialRealDense
sage: f = PolynomialRealDense(RR['x'], [1, 2, 3]); f
3.00000000000000*x^2 + 2.00000000000000*x + 1.00000000000000
sage: f.shift(10)
3.00000000000000*x^12 + 2.00000000000000*x^11 + x^10
sage: f.shift(-1)
3.00000000000000*x + 2.00000000000000
sage: f.shift(-10)
0

TESTS:

sage: f = RR['x'](0)
sage: f.shift(3).is_zero()
True
sage: f.shift(-3).is_zero()
True

truncate(n)

Returns the polynomial of degree 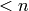which is equivalent to self modulo .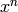

EXAMPLES:

sage: from sage.rings.polynomial.polynomial_real_mpfr_dense import PolynomialRealDense
sage: f = PolynomialRealDense(RealField(10)['x'], [1, 2, 4, 8])
sage: f.truncate(3)
4.0*x^2 + 2.0*x + 1.0
sage: f.truncate(100)
8.0*x^3 + 4.0*x^2 + 2.0*x + 1.0
sage: f.truncate(1)
1.0
sage: f.truncate(0)
0

truncate_abs(bound)

Truncate all high order coefficients below bound.

EXAMPLES:

sage: from sage.rings.polynomial.polynomial_real_mpfr_dense import PolynomialRealDense
sage: f = PolynomialRealDense(RealField(10)['x'], [10^-k for k in range(10)])
sage: f
1.0e-9*x^9 + 1.0e-8*x^8 + 1.0e-7*x^7 + 1.0e-6*x^6 + 0.000010*x^5 + 0.00010*x^4 + 0.0010*x^3 + 0.010*x^2 + 0.10*x + 1.0
sage: f.truncate_abs(0.5e-6)
1.0e-6*x^6 + 0.000010*x^5 + 0.00010*x^4 + 0.0010*x^3 + 0.010*x^2 + 0.10*x + 1.0
sage: f.truncate_abs(10.0)
0
sage: f.truncate_abs(1e-100) == f
True

sage.rings.polynomial.polynomial_real_mpfr_dense.make_PolynomialRealDense(parent, data)

EXAMPLES:

sage: from sage.rings.polynomial.polynomial_real_mpfr_dense import make_PolynomialRealDense
sage: make_PolynomialRealDense(RR['x'], [1,2,3])
3.00000000000000*x^2 + 2.00000000000000*x + 1.00000000000000