AUTHORS:
TESTS:
sage: R.<x> = ZZ[]
sage: f = x^5 + 2*x^2 + (-1)
sage: f == loads(dumps(f))
True
Bases: sage.categories.map.Map
This class is used for conversion from a polynomial ring to its base ring.
It calls the constant_coefficient method, which can be optimized for a particular polynomial type.
Bases: sage.structure.element.CommutativeAlgebraElement
A polynomial.
EXAMPLE:
sage: R.<y> = QQ['y']
sage: S.<x> = R['x']
sage: f = x*y; f
y*x
sage: type(f)
<type 'sage.rings.polynomial.polynomial_element.Polynomial_generic_dense'>
sage: p = (y+1)^10; p(1)
1024
Returns the generator of this polynomial ring, which is the (only) argument used when calling self.
EXAMPLES:
sage: R.<x> = QQ[]
sage: x.args()
(x,)
A constant polynomial has no variables, but still takes a single argument.
sage: R(2).args()
(x,)
Return a copy of this polynomial but with coefficients in R, if there is a natural map from coefficient ring of self to R.
EXAMPLES:
sage: R.<x> = QQ[]
sage: f = x^3 - 17*x + 3
sage: f.base_extend(GF(7))
...
TypeError: no such base extension
sage: f.change_ring(GF(7))
x^3 + 4*x + 3
Return the base ring of the parent of self.
EXAMPLES:
sage: R.<x> = ZZ[]
sage: x.base_ring()
Integer Ring
sage: (2*x+3).base_ring()
Integer Ring
Return a copy of this polynomial but with coefficients in R, if at all possible.
EXAMPLES:
sage: K.<z> = CyclotomicField(3)
sage: f = K.defining_polynomial()
sage: f.change_ring(GF(7))
x^2 + x + 1
Return a new polynomial over the same base ring but in a different variable.
EXAMPLES:
sage: x = polygen(QQ,'x')
sage: f = -2/7*x^3 + (2/3)*x - 19/993; f
-2/7*x^3 + 2/3*x - 19/993
sage: f.change_variable_name('theta')
-2/7*theta^3 + 2/3*theta - 19/993
Return the coefficients of the monomials appearing in self.
EXAMPLES:
sage: _.<x> = PolynomialRing(ZZ)
sage: f = x^4+2*x^2+1
sage: f.coefficients()
[1, 2, 1]
Returns self.list().
(It is potentially slightly faster to use self.list() directly.)
EXAMPLES:
sage: x = QQ['x'].0
sage: f = 10*x^3 + 5*x + 2/17
sage: f.coeffs()
[2/17, 5, 0, 10]
Return the complex roots of this polynomial, without multiplicities.
Calls self.roots(ring=CC), unless this is a polynomial with floating-point coefficients, in which case it is uses the appropriate precision from the input coefficients.
EXAMPLES:
sage: x = polygen(ZZ)
sage: (x^3 - 1).complex_roots() # note: low order bits slightly different on ppc.
[1.00000000000000, -0.500000000000000 - 0.86602540378443...*I, -0.500000000000000 + 0.86602540378443...*I]
TESTS:
sage: x = polygen(RR)
sage: (x^3 - 1).complex_roots()[0].parent()
Complex Field with 53 bits of precision
sage: x = polygen(RDF)
sage: (x^3 - 1).complex_roots()[0].parent()
Complex Double Field
sage: x = polygen(RealField(200))
sage: (x^3 - 1).complex_roots()[0].parent()
Complex Field with 200 bits of precision
sage: x = polygen(CDF)
sage: (x^3 - 1).complex_roots()[0].parent()
Complex Double Field
sage: x = polygen(ComplexField(200))
sage: (x^3 - 1).complex_roots()[0].parent()
Complex Field with 200 bits of precision
sage: x=polygen(ZZ,'x'); v=(x^2-x-1).complex_roots()
sage: v[0].parent() is CC
True
Return the constant coefficient of this polynomial.
OUTPUT: element of base ring
EXAMPLES:
sage: R.<x> = QQ[]
sage: f = -2*x^3 + 2*x - 1/3
sage: f.constant_coefficient()
-1/3
Return the degree of this polynomial. The zero polynomial has degree -1.
EXAMPLES:
sage: x = ZZ['x'].0
sage: f = x^93 + 2*x + 1
sage: f.degree()
93
sage: x = PolynomialRing(QQ, 'x', sparse=True).0
sage: f = x^100000
sage: f.degree()
100000
sage: x = QQ['x'].0
sage: f = 2006*x^2006 - x^2 + 3
sage: f.degree()
2006
sage: f = 0*x
sage: f.degree()
-1
sage: f = x + 33
sage: f.degree()
1
AUTHORS:
Return a denominator of self.
First, the lcm of the denominators of the entries of self is computed and returned. If this computation fails, the unit of the parent of self is returned.
Note that some subclasses may implement their own denominator function. For example, see sage.rings.polynomial.polynomial_element_generic.Polynomial_rational_dense
Warning
This is not the denominator of the rational function defined by self, which would always be 1 since self is a polynomial.
EXAMPLES:
First we compute the denominator of a polynomial with integer coefficients, which is of course 1.
sage: R.<x> = ZZ[]
sage: f = x^3 + 17*x + 1
sage: f.denominator()
1
Next we compute the denominator of a polynomial with rational coefficients.
sage: R.<x> = PolynomialRing(QQ)
sage: f = (1/17)*x^19 - (2/3)*x + 1/3; f
1/17*x^19 - 2/3*x + 1/3
sage: f.denominator()
51
Finally, we try to compute the denominator of a polynomial with coefficients in the real numbers, which is a ring whose elements do not have a denominator method.
sage: R.<x> = RR[]
sage: f = x + RR('0.3'); f
x + 0.300000000000000
sage: f.denominator()
1.00000000000000
The formal derivative of this polynomial, with respect to variables supplied in args.
Multiple variables and iteration counts may be supplied; see documentation for the global derivative() function for more details.
See also
_derivative()
EXAMPLES:
sage: R.<x> = PolynomialRing(QQ)
sage: g = -x^4 + x^2/2 - x
sage: g.derivative()
-4*x^3 + x - 1
sage: g.derivative(x)
-4*x^3 + x - 1
sage: g.derivative(x, x)
-12*x^2 + 1
sage: g.derivative(x, 2)
-12*x^2 + 1
sage: R.<t> = PolynomialRing(ZZ)
sage: S.<x> = PolynomialRing(R)
sage: f = t^3*x^2 + t^4*x^3
sage: f.derivative()
3*t^4*x^2 + 2*t^3*x
sage: f.derivative(x)
3*t^4*x^2 + 2*t^3*x
sage: f.derivative(t)
4*t^3*x^3 + 3*t^2*x^2
Return a sparse dictionary representation of this univariate polynomial.
EXAMPLES:
sage: R.<x> = QQ[]
sage: f = x^3 + -1/7*x + 13
sage: f.dict()
{0: 13, 1: -1/7, 3: 1}
Returns the discriminant of self.
The discriminant is
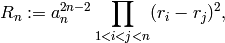
where  is the degree of self,
is the degree of self, 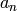 is the
leading coefficient of self and the roots of self are
is the
leading coefficient of self and the roots of self are
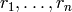 .
.
OUTPUT: An element of the base ring of the polynomial ring.
Note
Uses the identity 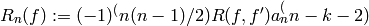 , where
, where  is the degree of self,
is the degree of self,
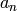 is the leading coefficient of self,
is the leading coefficient of self, 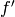 is the derivative of
is the derivative of  , and
, and  is the degree
of
is the degree
of 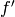 . Calls resultant().
. Calls resultant().
EXAMPLES:
In the case of elliptic curves in special form, the discriminant is easy to calculate:
sage: R.<x> = QQ[]
sage: f = x^3 + x + 1
sage: d = f.discriminant(); d
-31
sage: d.parent() is QQ
True
sage: EllipticCurve([1, 1]).discriminant()/16
-31
sage: R.<x> = QQ[]
sage: f = 2*x^3 + x + 1
sage: d = f.discriminant(); d
-116
We can also compute discriminants over univariate and multivariate polynomial rings, provided that PARI’s variable ordering requirements are respected. Usually, your discriminants will work if you always ask for them in the variable x:
sage: R.<a> = QQ[]
sage: S.<x> = R[]
sage: f = a*x + x + a + 1
sage: d = f.discriminant(); d
1
sage: d.parent() is R
True
sage: R.<a, b> = QQ[]
sage: S.<x> = R[]
sage: f = x^2 + a + b
sage: d = f.discriminant(); d
-4*a - 4*b
sage: d.parent() is R
True
Unfortunately Sage does not handle PARI’s variable ordering requirements gracefully, so the following fails:
sage: R.<x, y> = QQ[]
sage: S.<a> = R[]
sage: f = x^2 + a
sage: f.discriminant()
...
PariError: (8)
Return the exponents of the monomials appearing in self.
EXAMPLES:
sage: _.<x> = PolynomialRing(ZZ)
sage: f = x^4+2*x^2+1
sage: f.exponents()
[0, 2, 4]
Return the factorization of self over the base ring of this
polynomial. Factoring polynomials over
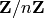 for
for  composite is at
the moment not implemented.
composite is at
the moment not implemented.
INPUT: a polynomial
OUTPUT:
Over a field the irreducible factors are all monic.
EXAMPLES:
We factor some polynomials over  .
.
sage: x = QQ['x'].0
sage: f = (x^3 - 1)^2
sage: f.factor()
(x - 1)^2 * (x^2 + x + 1)^2
Notice that over the field  the irreducible
factors are monic.
the irreducible
factors are monic.
sage: f = 10*x^5 - 1
sage: f.factor()
(10) * (x^5 - 1/10)
sage: f = 10*x^5 - 10
sage: f.factor()
(10) * (x - 1) * (x^4 + x^3 + x^2 + x + 1)
Over  the irreducible factors need not be
monic:
the irreducible factors need not be
monic:
sage: x = ZZ['x'].0
sage: f = 10*x^5 - 1
sage: f.factor()
10*x^5 - 1
We factor a non-monic polynomial over the finite field
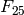 .
.
sage: k.<a> = GF(25)
sage: R.<x> = k[]
sage: f = 2*x^10 + 2*x + 2*a
sage: F = f.factor(); F
(2) * (x + a + 2) * (x^2 + 3*x + 4*a + 4) * (x^2 + (a + 1)*x + a + 2) * (x^5 + (3*a + 4)*x^4 + (3*a + 3)*x^3 + 2*a*x^2 + (3*a + 1)*x + 3*a + 1)
Notice that the unit factor is included when we multiply
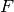 back out.
back out.
sage: expand(F)
2*x^10 + 2*x + 2*a
Factorization also works even if the variable of the finite field is nefariously labeled “x”.
sage: x = GF(3^2, 'a')['x'].0
sage: f = x^10 +7*x -13
sage: G = f.factor(); G
(x + a) * (x + 2*a + 1) * (x^4 + (a + 2)*x^3 + (2*a + 2)*x + 2) * (x^4 + 2*a*x^3 + (a + 1)*x + 2)
sage: prod(G) == f
True
sage: f.parent().base_ring()._assign_names(['a'])
sage: f.factor()
(x + a) * (x + 2*a + 1) * (x^4 + (a + 2)*x^3 + (2*a + 2)*x + 2) * (x^4 + 2*a*x^3 + (a + 1)*x + 2)
sage: k = GF(9,'x') # purposely calling it x to test robustness
sage: x = PolynomialRing(k,'x0').gen()
sage: f = x^3 + x + 1
sage: f.factor()
(x0 + 2) * (x0 + x) * (x0 + 2*x + 1)
sage: f = 0*x
sage: f.factor()
...
ValueError: factorization of 0 not defined
sage: f = x^0
sage: f.factor()
1
Arbitrary precision real and complex factorization:
sage: R.<x> = RealField(100)[]
sage: F = factor(x^2-3); F
(x - 1.7320508075688772935274463415) * (x + 1.7320508075688772935274463415)
sage: expand(F)
x^2 - 3.0000000000000000000000000000
sage: factor(x^2 + 1)
x^2 + 1.0000000000000000000000000000
sage: C = ComplexField(100)
sage: R.<x> = C[]
sage: F = factor(x^2+3); F
(x - 1.7320508075688772935274463415*I) * (x + 1.7320508075688772935274463415*I)
sage: expand(F)
x^2 + 3.0000000000000000000000000000
sage: factor(x^2+1)
(x - I) * (x + I)
sage: f = C.0 * (x^2 + 1) ; f
I*x^2 + I
sage: F = factor(f); F
(1.0000000000000000000000000000*I) * (x - I) * (x + I)
sage: expand(F)
I*x^2 + I
Over a complicated number field:
sage: x = polygen(QQ, 'x')
sage: f = x^6 + 10/7*x^5 - 867/49*x^4 - 76/245*x^3 + 3148/35*x^2 - 25944/245*x + 48771/1225
sage: K.<a> = NumberField(f)
sage: S.<T> = K[]
sage: ff = S(f); ff
T^6 + 10/7*T^5 - 867/49*T^4 - 76/245*T^3 + 3148/35*T^2 - 25944/245*T + 48771/1225
sage: F = ff.factor()
sage: len(F)
4
sage: F[:2]
[(T - a, 1), (T - 40085763200/924556084127*a^5 - 145475769880/924556084127*a^4 + 527617096480/924556084127*a^3 + 1289745809920/924556084127*a^2 - 3227142391585/924556084127*a - 401502691578/924556084127, 1)]
sage: expand(F)
T^6 + 10/7*T^5 - 867/49*T^4 - 76/245*T^3 + 3148/35*T^2 - 25944/245*T + 48771/1225
sage: f = x^2 - 1/3 ; K.<a> = NumberField(f) ; A.<T> = K[] ; g = A(x^2-1)
sage: g.factor()
(T - 1) * (T + 1)
sage: h = A(3*x^2-1) ; h.factor()
(3) * (T - a) * (T + a)
sage: h = A(x^2-1/3) ; h.factor()
(T - a) * (T + a)
Over the real double field:
sage: x = polygen(RDF)
sage: f = (x-1)^3
sage: f.factor() # random output (unfortunately)
(1.0*x - 1.00000859959) * (1.0*x^2 - 1.99999140041*x + 0.999991400484)
sage: (-2*x^2 - 1).factor()
(-2.0) * (x^2 + 0.5)
sage: (-2*x^2 - 1).factor().expand()
-2.0*x^2 - 1.0
Note that this factorization suffers from the roots function:
sage: f.roots() # random output (unfortunately)
[1.00000859959, 0.999995700205 + 7.44736245561e-06*I, 0.999995700205 - 7.44736245561e-06*I]
Over the complex double field. Because this is approximate, all factors will occur with multiplicity 1.
sage: x = CDF['x'].0; i = CDF.0
sage: f = (x^2 + 2*i)^3
sage: f.factor() # random low order bits
(1.0*x + -0.999994409957 + 1.00001040378*I) * (1.0*x + -0.999993785062 + 0.999989956987*I) * (1.0*x + -1.00001180498 + 0.999999639235*I) * (1.0*x + 0.999995530902 - 0.999987780431*I) * (1.0*x + 1.00001281704 - 1.00000223945*I) * (1.0*x + 0.999991652054 - 1.00000998012*I)
sage: f(-f.factor()[0][0][0]) # random low order bits
-2.38358052913e-14 - 2.57571741713e-14*I
Over a relative number field:
sage: x = QQ['x'].0
sage: L.<a> = CyclotomicField(3).extension(x^3 - 2)
sage: x = L['x'].0
sage: f = (x^3 + x + a)*(x^5 + x + L.1); f
x^8 + x^6 + a*x^5 + x^4 + zeta3*x^3 + x^2 + (a + zeta3)*x + zeta3*a
sage: f.factor()
(x^3 + x + a) * (x^5 + x + zeta3)
Factoring polynomials over 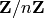 for
composite
for
composite  is not implemented:
is not implemented:
sage: R.<x> = PolynomialRing(Integers(35))
sage: f = (x^2+2*x+2)*(x^2+3*x+9)
sage: f.factor()
...
NotImplementedError: factorization of polynomials over rings with composite characteristic is not implemented
Factoring polynomials over QQbar and AA is implemented (see #8544):
sage: x = polygen(QQbar)
sage: (x^8-1).factor()
(x - 1) * (x - 0.7071067811865475? - 0.7071067811865475?*I) * (x - 0.7071067811865475? + 0.7071067811865475?*I) * (x - I) * (x + I) * (x + 0.7071067811865475? - 0.7071067811865475?*I) * (x + 0.7071067811865475? + 0.7071067811865475?*I) * (x + 1)
sage: (12*x^2-4).factor()
(12) * (x - 0.5773502691896258?) * (x + 0.5773502691896258?)
sage: x.parent()(-1).factor()
-1
sage: EllipticCurve('11a1').change_ring(QQbar).division_polynomial(5).factor()
(5) * (x - 16) * (x - 5) * (x - 1.959674775249769?) * (x - 1.427050983124843? - 3.665468789467727?*I) * (x - 1.427050983124843? + 3.665468789467727?*I) * (x + 0.9549150281252629? - 0.8652998037182486?*I) * (x + 0.9549150281252629? + 0.8652998037182486?*I) * (x + 1.927050983124843? - 1.677599044300515?*I) * (x + 1.927050983124843? + 1.677599044300515?*I) * (x + 2.959674775249769?) * (x + 6.545084971874737? - 7.106423590645660?*I) * (x + 6.545084971874737? + 7.106423590645660?*I)
sage: x = polygen(AA)
sage: (x^8+1).factor()
(x^2 - 1.847759065022574?*x + 1.000000000000000?) * (x^2 - 0.7653668647301795?*x + 1.000000000000000?) * (x^2 + 0.7653668647301795?*x + 1.000000000000000?) * (x^2 + 1.847759065022574?*x + 1.000000000000000?)
sage: x.parent()(3).factor()
3
sage: (12*x^2-4).factor()
(12) * (x - 0.5773502691896258?) * (x + 0.5773502691896258?)
sage: (12*x^2+4).factor()
(12) * (x^2 + 0.3333333333333334?)
sage: EllipticCurve('11a1').change_ring(AA).division_polynomial(5).factor()
(5) * (x - 16.00000000000000?) * (x - 5.000000000000000?) * (x - 1.959674775249769?) * (x + 2.959674775249769?) * (x^2 - 2.854101966249685?*x + 15.47213595499958?) * (x^2 + 1.909830056250526?*x + 1.660606461254312?) * (x^2 + 3.854101966249685?*x + 6.527864045000421?) * (x^2 + 13.09016994374948?*x + 93.33939353874569?)
TESTS:
This came up in ticket #7088:
sage: R.<x>=PolynomialRing(ZZ)
sage: f = 12*x^10 + x^9 + 432*x^3 + 9011
sage: g = 13*x^11 + 89*x^3 + 1
sage: F = f^2 * g^3
sage: F = f^2 * g^3; F.factor()
(12*x^10 + x^9 + 432*x^3 + 9011)^2 * (13*x^11 + 89*x^3 + 1)^3
sage: F = f^2 * g^3 * 7; F.factor()
7 * (12*x^10 + x^9 + 432*x^3 + 9011)^2 * (13*x^11 + 89*x^3 + 1)^3
This example came up in ticket #7097:
sage: x = polygen(QQ) sage: f = 8*x^9 + 42*x^6 + 6*x^3 - 1 sage: g = x^24 - 12*x^23 + 72*x^22 - 286*x^21 + 849*x^20 - 2022*x^19 + 4034*x^18 - 6894*x^17 + 10182*x^16 - 13048*x^15 + 14532*x^14 - 13974*x^13 + 11365*x^12 - 7578*x^11 + 4038*x^10 - 1766*x^9 + 762*x^8 - 408*x^7 + 236*x^6 - 126*x^5 + 69*x^4 - 38*x^3 + 18*x^2 - 6*x + 1 sage: assert g.is_irreducible() sage: K.<a> = NumberField(g) sage: len(f.roots(K)) 9 sage: f.factor() (8) * (x^3 + 1/4) * (x^6 + 5*x^3 - 1/2) sage: f.change_ring(K).factor() (8) * (x - 3260097/3158212*a^22 + 35861067/3158212*a^21 - 197810817/3158212*a^20 + 722970825/3158212*a^19 - 1980508347/3158212*a^18 + 4374189477/3158212*a^17 - 4059860553/1579106*a^16 + 6442403031/1579106*a^15 - 17542341771/3158212*a^14 + 20537782665/3158212*a^13 - 20658463789/3158212*a^12 + 17502836649/3158212*a^11 - 11908953451/3158212*a^10 + 6086953981/3158212*a^9 - 559822335/789553*a^8 + 194545353/789553*a^7 - 505969453/3158212*a^6 + 338959407/3158212*a^5 - 155204647/3158212*a^4 + 79628015/3158212*a^3 - 57339525/3158212*a^2 + 26692783/3158212*a - 1636338/789553) * ... sage: f = QQbar[‘x’](1) sage: f.factor() 1
Returns the number of non-zero coefficients of self.
EXAMPLES:
sage: R.<x> = ZZ[]
sage: f = x^3 - x
sage: f.hamming_weight()
2
sage: R(0).hamming_weight()
0
sage: f = (x+1)^100
sage: f.hamming_weight()
101
sage: S = GF(5)['y']
sage: S(f).hamming_weight()
5
sage: cyclotomic_polynomial(105).hamming_weight()
33
Return the integral of this polynomial.
Note
The integral is always chosen so the constant term is 0.
EXAMPLES:
sage: R.<x> = ZZ[]
sage: R(0).integral()
0
sage: f = R(2).integral(); f
2*x
Note that since the integral is defined over the same base ring the integral is actually in the base ring.
sage: f.parent()
Univariate Polynomial Ring in x over Integer Ring
If the integral isn’t defined over the same base ring, then the base ring is extended:
sage: f = x^3 + x - 2
sage: g = f.integral(); g
1/4*x^4 + 1/2*x^2 - 2*x
sage: g.parent()
Univariate Polynomial Ring in x over Rational Field
Inverts the polynomial a with respect to m, or raises a ValueError if no such inverse exists. The parameter m may be either a single polynomial or an ideal (for consistency with inverse_mod in other rings).
EXAMPLES:
sage: S.<t> = QQ[]
sage: f = inverse_mod(t^2 + 1, t^3 + 1); f
-1/2*t^2 - 1/2*t + 1/2
sage: f * (t^2 + 1) % (t^3 + 1)
1
sage: f = t.inverse_mod((t+1)^7); f
-t^6 - 7*t^5 - 21*t^4 - 35*t^3 - 35*t^2 - 21*t - 7
sage: (f * t) + (t+1)^7
1
sage: t.inverse_mod(S.ideal((t + 1)^7)) == f
True
It also works over in-exact rings, but note that due to rounding error the product is only guaranteed to be within epsilon of the constant polynomial 1.
sage: R.<x> = RDF[]
sage: f = inverse_mod(x^2 + 1, x^5 + x + 1); f
0.4*x^4 - 0.2*x^3 - 0.4*x^2 + 0.2*x + 0.8
sage: f * (x^2 + 1) % (x^5 + x + 1)
2.22044604925e-16*x^2 + 1.11022302463e-16*x + 1.0
sage: f = inverse_mod(x^3 - x + 1, x - 2); f
0.142857142857
sage: f * (x^3 - x + 1) % (x - 2)
1.0
ALGORITHM: Solve the system as + mt = 1, returning s as the inverse of a mod m.
Uses the Euclidean algorithm for exact rings, and solves a linear system for the coefficients of s and t for inexact rings (as the Euclidean algorithm may not converge in that case).
AUTHORS:
EXAMPLES:
sage: R.<x> = QQ[]
sage: f = x - 90283
sage: f.inverse_of_unit()
...
ValueError: self is not a unit.
sage: f = R(-90283); g = f.inverse_of_unit(); g
-1/90283
sage: parent(g)
Univariate Polynomial Ring in x over Rational Field
Return True if this is a constant polynomial.
OUTPUT:
EXAMPLES:
sage: R.<x> = ZZ[]
sage: x.is_constant()
False
sage: R(2).is_constant()
True
sage: R(0).is_constant()
True
Return True if this polynomial is the distinguished generator of the parent polynomial ring.
EXAMPLES:
sage: R.<x> = QQ[]
sage: R(1).is_gen()
False
sage: R(x).is_gen()
True
Important - this function doesn’t return True if self equals the generator; it returns True if self is the generator.
sage: f = R([0,1]); f
x
sage: f.is_gen()
False
sage: f is x
False
sage: f == x
True
Return True precisely if this polynomial is irreducible over its
base ring. Testing irreducibility over
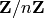 for composite
for composite  is not
implemented.
is not
implemented.
The function returns False for polynomials which are units, and raises an exception for the zero polynomial.
EXAMPLES:
sage: R.<x> = ZZ[]
sage: (x^3 + 1).is_irreducible()
False
sage: (x^2 - 1).is_irreducible()
False
sage: (x^3 + 2).is_irreducible()
True
sage: R(0).is_irreducible()
...
ValueError: self must be nonzero
The base ring does matter: for example, 2x is irreducible as a polynomial in QQ[x], but not in ZZ[x]:
sage: R.<x> = ZZ[] sage: R(2*x).is_irreducible() False sage: R.<x> = QQ[] sage: R(2*x).is_irreducible() True
TESTS:
sage: F.<t> = NumberField(x^2-5)
sage: Fx.<xF> = PolynomialRing(F)
sage: f = Fx([2*t - 5, 5*t - 10, 3*t - 6, -t, -t + 2, 1])
sage: f.is_irreducible()
False
sage: f = Fx([2*t - 3, 5*t - 10, 3*t - 6, -t, -t + 2, 1])
sage: f.is_irreducible()
True
Returns True if this polynomial is monic. The zero polynomial is by definition not monic.
EXAMPLES:
sage: x = QQ['x'].0
sage: f = x + 33
sage: f.is_monic()
True
sage: f = 0*x
sage: f.is_monic()
False
sage: f = 3*x^3 + x^4 + x^2
sage: f.is_monic()
True
sage: f = 2*x^2 + x^3 + 56*x^5
sage: f.is_monic()
False
AUTHORS:
Returns True if this is a monomial.
EXAMPLES:
sage: R.<x> = QQ[]
sage: x.is_monomial()
True
sage: (x+1).is_monomial()
False
sage: (x^2).is_monomial()
True
Return True if this polynomial is nilpotent.
EXAMPLES:
sage: R = Integers(12)
sage: S.<x> = R[]
sage: f = 5 + 6*x
sage: f.is_nilpotent()
False
sage: f = 6 + 6*x^2
sage: f.is_nilpotent()
True
sage: f^2
0
EXERCISE (Atiyah-McDonald, Ch 1): Let ![A[x]](../../../_images/math/4d57b2e7466f9447d4489dc8ef949681ab435b45.png) be a
polynomial ring in one variable. Then
be a
polynomial ring in one variable. Then
![f=\sum a_i x^i \in A[x]](../../../_images/math/226bd1330dd49ad17a9094a0ff3325bd0f11826a.png) is nilpotent if and only if
every
is nilpotent if and only if
every 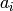 is nilpotent.
is nilpotent.
Returns True if the polynomial is primitive. The semantics of “primitive” depend on the polynomial coefficients.
 over a finite field
over a finite field
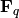 is primitive if it is irreducible and its root in
is primitive if it is irreducible and its root in
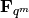 generates the multiplicative group
generates the multiplicative group 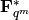 .
.Calling 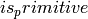 on a polynomial over an infinite field will
raise an error.
on a polynomial over an infinite field will
raise an error.
The additional inputs to this function are to speed up computation for field semantics (see note).
INPUTS:
- n (default: None) - if provided, should equal
where self.parent() is the field with
elements; otherwise it will be computed.
- n_prime_divs (default: None) - if provided, should be a list of the prime divisors of n; otherwise it will be computed.
Note
Computation of the prime divisors of n can dominate the running time of this method, so performing this computation externally (e.g. pdivs=n.prime_divisors()) is a good idea for repeated calls to is_primitive for polynomials of the same degree.
Results may be incorrect if the wrong n and/or factorization are provided.
EXAMPLES:
Field semantics examples.
::
sage: R.<x> = GF(2)['x']
sage: f = x^4+x^3+x^2+x+1
sage: f.is_irreducible(), f.is_primitive()
(True, False)
sage: f = x^3+x+1
sage: f.is_irreducible(), f.is_primitive()
(True, True)
sage: R.<x> = GF(3)[]
sage: f = x^3-x+1
sage: f.is_irreducible(), f.is_primitive()
(True, True)
sage: f = x^2+1
sage: f.is_irreducible(), f.is_primitive()
(True, False)
sage: R.<x> = GF(5)[]
sage: f = x^2+x+1
sage: f.is_primitive()
False
sage: f = x^2-x+2
sage: f.is_primitive()
True
sage: x=polygen(QQ); f=x^2+1
sage: f.is_primitive()
Traceback (most recent call last):
...
NotImplementedError: is_primitive() not defined for polynomials over infinite fields.
Ring semantics examples.
::
sage: x=polygen(ZZ)
sage: f = 5*x^2+2
sage: f.is_primitive()
True
sage: f = 5*x^2+5
sage: f.is_primitive()
False
sage: K=NumberField(x^2+5,'a')
sage: R=K.ring_of_integers()
sage: a=R.gen(1)
sage: a^2
-5
sage: f=a*x+2
sage: f.is_primitive()
True
sage: f=(1+a)*x+2
sage: f.is_primitive()
False
sage: x=polygen(Integers(10));
sage: f=5*x^2+2
sage: #f.is_primitive() #BUG:: elsewhere in Sage, should return True
sage: f=4*x^2+2
sage: #f.is_primitive() #BUG:: elsewhere in Sage, should return False
TESTS:
sage: R.<x> = GF(2)['x']
sage: f = x^4+x^3+x^2+x+1
sage: f.is_primitive(15)
False
sage: f.is_primitive(15, [3,5])
False
sage: f.is_primitive(n_prime_divs=[3,5])
False
sage: f = x^3+x+1
sage: f.is_primitive(7, [7])
True
sage: R.<x> = GF(3)[]
sage: f = x^3-x+1
sage: f.is_primitive(26, [2,13])
True
sage: f = x^2+1
sage: f.is_primitive(8, [2])
False
sage: R.<x> = GF(5)[]
sage: f = x^2+x+1
sage: f.is_primitive(24, [2,3])
False
sage: f = x^2-x+2
sage: f.is_primitive(24, [2,3])
True
sage: x=polygen(Integers(103)); f=x^2+1
sage: f.is_primitive()
False
Returns whether or not polynomial is square. If the optional argument root is True, then also returns the square root (or None, if the polynomial is not square).
INPUT:
OUTPUT:
EXAMPLES:
sage: R.<x> = PolynomialRing(QQ)
sage: f = 12*(x+1)^2 * (x+3)^2
sage: S.<y> = PolynomialRing(RR)
sage: g = 12*(y+1)^2 * (y+3)^2
sage: f.is_square()
False
sage: f.is_square(root=True)
(False, None)
sage: g.is_square()
True
sage: h = f/3; h
4*x^4 + 32*x^3 + 88*x^2 + 96*x + 36
sage: h.is_square(root=True)
(True, 2*x^2 + 8*x + 6)
TESTS:
Make sure ticket #9093 is fixed:
sage: R(1).is_square()
True
sage: R(4/9).is_square()
True
sage: R(-1/3).is_square()
False
sage: R(0).is_square()
True
Return True if this polynomial is square free.
EXAMPLES:
sage: x = polygen(QQ)
sage: f = (x-1)*(x-2)*(x^2-5)*(x^17-3); f
x^21 - 3*x^20 - 3*x^19 + 15*x^18 - 10*x^17 - 3*x^4 + 9*x^3 + 9*x^2 - 45*x + 30
sage: f.is_squarefree()
True
sage: (f*(x^2-5)).is_squarefree()
False
Return True if this polynomial is a unit.
EXAMPLES:
sage: a = Integers(90384098234^3)
sage: b = a(2*191*236607587)
sage: b.is_nilpotent()
True
sage: R.<x> = a[]
sage: f = 3 + b*x + b^2*x^2
sage: f.is_unit()
True
sage: f = 3 + b*x + b^2*x^2 + 17*x^3
sage: f.is_unit()
False
EXERCISE (Atiyah-McDonald, Ch 1): Let ![A[x]](../../../_images/math/4d57b2e7466f9447d4489dc8ef949681ab435b45.png) be a
polynomial ring in one variable. Then
be a
polynomial ring in one variable. Then
![f=\sum a_i x^i \in A[x]](../../../_images/math/226bd1330dd49ad17a9094a0ff3325bd0f11826a.png) is a unit if and only if
is a unit if and only if
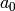 is a unit and
is a unit and 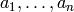 are
nilpotent.
are
nilpotent.
A decorator to be used on binary operation methods that should operate on elements of the same parent. If the parents of the arguments differ, coercion is performed, then the method is re-looked up by name on the first argument.
In short, using the NamedBinopMethod (alias coerce_binop) decorator on a method gives it the exact same semantics of the basic arithmetic operations like _add_, _sub_, etc. in that both operands are guaranteed to have exactly the same parent.
Return the leading coefficient of this polynomial.
OUTPUT: element of the base ring
EXAMPLES:
sage: R.<x> = QQ[]
sage: f = (-2/5)*x^3 + 2*x - 1/3
sage: f.leading_coefficient()
-2/5
Return a new copy of the list of the underlying elements of self.
EXAMPLES:
sage: R.<x> = QQ[]
sage: f = (-2/5)*x^3 + 2*x - 1/3
sage: v = f.list(); v
[-1/3, 2, 0, -2/5]
Note that v is a list, it is mutable, and each call to the list method returns a new list:
sage: type(v)
<type 'list'>
sage: v[0] = 5
sage: f.list()
[-1/3, 2, 0, -2/5]
Here is an example with a generic polynomial ring:
sage: R.<x> = QQ[]
sage: S.<y> = R[]
sage: f = y^3 + x*y -3*x; f
y^3 + x*y - 3*x
sage: type(f)
<type 'sage.rings.polynomial.polynomial_element.Polynomial_generic_dense'>
sage: v = f.list(); v
[-3*x, x, 0, 1]
sage: v[0] = 10
sage: f.list()
[-3*x, x, 0, 1]
Return this polynomial divided by its leading coefficient. Does not change this polynomial.
EXAMPLES:
sage: x = QQ['x'].0
sage: f = 2*x^2 + x^3 + 56*x^5
sage: f.monic()
x^5 + 1/56*x^3 + 1/28*x^2
sage: f = (1/4)*x^2 + 3*x + 1
sage: f.monic()
x^2 + 12*x + 4
The following happens because 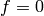 cannot be made into a
monic polynomial
cannot be made into a
monic polynomial
sage: f = 0*x
sage: f.monic()
...
ZeroDivisionError: rational division by zero
Notice that the monic version of a polynomial over the integers is defined over the rationals.
sage: x = ZZ['x'].0
sage: f = 3*x^19 + x^2 - 37
sage: g = f.monic(); g
x^19 + 1/3*x^2 - 37/3
sage: g.parent()
Univariate Polynomial Ring in x over Rational Field
AUTHORS:
Note: This function is deprecated. It will be removed in a future release of Sage. Please use the .variable_name() function instead.
Return the string variable name of the indeterminate of this polynomial.
EXAMPLES:
sage: R.<theta> = ZZ[];
sage: f = (2-theta)^3; f
-theta^3 + 6*theta^2 - 12*theta + 8
sage: f.name()
doctest:...: DeprecationWarning: This function is deprecated. It will be removed in a future release of Sage. Please use the .variable_name() function instead.
'theta'
Return a list of n iterative approximations to a root of this polynomial, computed using the Newton-Raphson method.
The Newton-Raphson method is an iterative root-finding algorithm. For f(x) a polynomial, as is the case here, this is essentially the same as Horner’s method.
INPUT:
OUTPUT: A list of numbers hopefully approximating a root of f(x)=0.
If one of the iterates is a critical point of f then a ZeroDivisionError exception is raised.
EXAMPLES:
sage: x = PolynomialRing(RealField(), 'x').gen()
sage: f = x^2 - 2
sage: f.newton_raphson(4, 1)
[1.50000000000000, 1.41666666666667, 1.41421568627451, 1.41421356237469]
AUTHORS:
Return the  -adic slopes of the Newton polygon of self,
when this makes sense.
-adic slopes of the Newton polygon of self,
when this makes sense.
OUTPUT: list of rational numbers
EXAMPLES:
sage: x = QQ['x'].0
sage: f = x^3 + 2
sage: f.newton_slopes(2)
[1/3, 1/3, 1/3]
ALGORITHM: Uses PARI.
Return the  -norm of this polynomial.
-norm of this polynomial.
DEFINITION: For integer  , the
, the  -norm of a
polynomial is the
-norm of a
polynomial is the  th root of the sum of the
th root of the sum of the
 th powers of the absolute values of the coefficients of
the polynomial.
th powers of the absolute values of the coefficients of
the polynomial.
INPUT:
EXAMPLES:
sage: R.<x> =RR[]
sage: f = x^6 + x^2 + -x^4 - 2*x^3
sage: f.norm(2)
2.64575131106459
sage: (sqrt(1^2 + 1^2 + (-1)^2 + (-2)^2)).n()
2.64575131106459
sage: f.norm(1)
5.00000000000000
sage: f.norm(infinity)
2.00000000000000
sage: f.norm(-1)
...
ValueError: The degree of the norm must be positive
TESTS:
sage: R.<x> = RR[]
sage: f = x^6 + x^2 + -x^4 -x^3
sage: f.norm(int(2))
2.00000000000000
AUTHORS:
Return a numerator of self computed as self * self.denominator()
Note that some subclases may implement its own numerator function. For example, see sage.rings.polynomial.polynomial_element_generic.Polynomial_rational_dense
Warning
This is not the numerator of the rational function defined by self, which would always be self since self is a polynomial.
EXAMPLES:
First we compute the numerator of a polynomial with integer coefficients, which is of course self.
sage: R.<x> = ZZ[]
sage: f = x^3 + 17*x + 1
sage: f.numerator()
x^3 + 17*x + 1
sage: f == f.numerator()
True
Next we compute the numerator of a polynomial with rational coefficients.
sage: R.<x> = PolynomialRing(QQ)
sage: f = (1/17)*x^19 - (2/3)*x + 1/3; f
1/17*x^19 - 2/3*x + 1/3
sage: f.numerator()
3*x^19 - 34*x + 17
sage: f == f.numerator()
False
We try to compute the denominator of a polynomial with coefficients in the real numbers, which is a ring whose elements do not have a denominator method.
sage: R.<x> = RR[]
sage: f = x + RR('0.3'); f
x + 0.300000000000000
sage: f.numerator()
x + 0.300000000000000
We check that the computation the numerator and denominator are valid
sage: K=NumberField(symbolic_expression('x^3+2'),'a')['s,t']['x']
sage: f=K.random_element()
sage: f.numerator() / f.denominator() == f
True
sage: R=RR['x']
sage: f=R.random_element()
sage: f.numerator() / f.denominator() == f
True
This is the same as the valuation of self at p. See the documentation for self.valuation.
EXAMPLES:
sage: P,x=PolynomialRing(ZZ,'x').objgen()
sage: (x^2+x).ord(x+1)
1
Return list of coefficients of self up to (but not including)
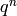 .
.
Includes 0’s in the list on the right so that the list has length
 .
.
INPUT:
EXAMPLES:
sage: x = polygen(QQ)
sage: f = 1 + x^3 + 23*x^5
sage: f.padded_list()
[1, 0, 0, 1, 0, 23]
sage: f.padded_list(10)
[1, 0, 0, 1, 0, 23, 0, 0, 0, 0]
sage: len(f.padded_list(10))
10
sage: f.padded_list(3)
[1, 0, 0]
sage: f.padded_list(0)
[]
sage: f.padded_list(-1)
...
ValueError: n must be at least 0
Return a plot of this polynomial.
INPUT:
OUTPUT: returns a graphic object.
EXAMPLES:
sage: x = polygen(GF(389))
sage: plot(x^2 + 1, rgbcolor=(0,0,1))
sage: x = polygen(QQ)
sage: plot(x^2 + 1, rgbcolor=(1,0,0))
Let var be one of the variables of the parent of self. This returns self viewed as a univariate polynomial in var over the polynomial ring generated by all the other variables of the parent.
For univariate polynomials, if var is the generator of the parent ring, we return this polynomial, otherwise raise an error.
EXAMPLES:
sage: R.<x> = QQ[]
sage: (x+1).polynomial(x)
x + 1
TESTS:
sage: x.polynomial(1)
...
ValueError: given variable is not the generator of parent.
Return the precision of this polynomial. This is always infinity, since polynomials are of infinite precision by definition (there is no big-oh).
EXAMPLES:
sage: x = polygen(ZZ)
sage: (x^5 + x + 1).prec()
+Infinity
sage: x.prec()
+Infinity
Returns the radical of self; over a field, this is the product of the distinct irreducible factors of self. (This is also sometimes called the “square-free part” of self, but that term is ambiguous; it is sometimes used to mean the quotient of self by its maximal square factor.)
EXAMPLES:
sage: P.<x> = ZZ[]
sage: t = (x^2-x+1)^3 * (3*x-1)^2
sage: t.radical()
3*x^3 - 4*x^2 + 4*x - 1
If self has a factor of multiplicity divisible by the characteristic (see Trac 8736):
sage: P.<x> = GF(2)[]
sage: (x^3 + x^2).radical()
x^2 + x
Return the real roots of this polynomial, without multiplicities.
Calls self.roots(ring=RR), unless this is a polynomial with floating-point real coefficients, in which case it calls self.roots().
EXAMPLES:
sage: x = polygen(ZZ)
sage: (x^2 - x - 1).real_roots()
[-0.618033988749895, 1.61803398874989]
TESTS:
sage: x = polygen(RealField(100))
sage: (x^2 - x - 1).real_roots()[0].parent()
Real Field with 100 bits of precision
sage: x = polygen(RDF)
sage: (x^2 - x - 1).real_roots()[0].parent()
Real Double Field
sage: x=polygen(ZZ,'x'); v=(x^2-x-1).real_roots()
sage: v[0].parent() is RR
True
A decorator to be used on binary operation methods that should operate on elements of the same parent. If the parents of the arguments differ, coercion is performed, then the method is re-looked up by name on the first argument.
In short, using the NamedBinopMethod (alias coerce_binop) decorator on a method gives it the exact same semantics of the basic arithmetic operations like _add_, _sub_, etc. in that both operands are guaranteed to have exactly the same parent.
Return polynomial but with the coefficients reversed.
If an optional degree argument is given the coefficient list will be truncated or zero padded as necessary and the reverse polynomial will have the specified degree.
EXAMPLES:
sage: R.<x> = ZZ[]; S.<y> = R[]
sage: f = y^3 + x*y -3*x; f
y^3 + x*y - 3*x
sage: f.reverse()
-3*x*y^3 + x*y^2 + 1
sage: f.reverse(degree=2)
-3*x*y^2 + x*y
sage: f.reverse(degree=5)
-3*x*y^5 + x*y^4 + y^2
TESTS:
sage: f.reverse(degree=1.5r)
...
ValueError: degree argument must be a non-negative integer, got 1.5
Return the field generated by the roots of the irreducible polynomial self. The output is either a number field, relative number field, a quotient of a polynomial ring over a field, or the fraction field of the base ring.
EXAMPLES:
sage: R.<x> = QQ['x']
sage: f = x^3 + x + 17
sage: f.root_field('a')
Number Field in a with defining polynomial x^3 + x + 17
sage: R.<x> = QQ['x']
sage: f = x - 3
sage: f.root_field('b')
Rational Field
sage: R.<x> = ZZ['x']
sage: f = x^3 + x + 17
sage: f.root_field('b')
Number Field in b with defining polynomial x^3 + x + 17
sage: y = QQ['x'].0
sage: L.<a> = NumberField(y^3-2)
sage: R.<x> = L['x']
sage: f = x^3 + x + 17
sage: f.root_field('c')
Number Field in c with defining polynomial x^3 + x + 17 over its base field
sage: R.<x> = PolynomialRing(GF(9,'a'))
sage: f = x^3 + x^2 + 8
sage: K.<alpha> = f.root_field(); K
Univariate Quotient Polynomial Ring in alpha over Finite Field in a of size 3^2 with modulus x^3 + x^2 + 2
sage: alpha^2 + 1
alpha^2 + 1
sage: alpha^3 + alpha^2
1
sage: R.<x> = QQ[]
sage: f = x^2
sage: K.<alpha> = f.root_field()
...
ValueError: polynomial must be irreducible
TESTS:
sage: (PolynomialRing(Integers(31),name='x').0+5).root_field('a')
Ring of integers modulo 31
Return the roots of this polynomial (by default, in the base ring of this polynomial).
INPUT:
By default, this finds all the roots that lie in the base ring of the polynomial. However, the ring parameter can be used to specify a ring to look for roots in.
If the polynomial and the output ring are both exact (integers, rationals, finite fields, etc.), then the output should always be correct (or raise an exception, if that case is not yet handled).
If the output ring is approximate (floating-point real or complex numbers), then the answer will be estimated numerically, using floating-point arithmetic of at least the precision of the output ring. If the polynomial is ill-conditioned, meaning that a small change in the coefficients of the polynomial will lead to a relatively large change in the location of the roots, this may give poor results. Distinct roots may be returned as multiple roots, multiple roots may be returned as distinct roots, real roots may be lost entirely (because the numerical estimate thinks they are complex roots). Note that polynomials with multiple roots are always ill-conditioned; there’s a footnote at the end of the docstring about this.
If the output ring is a RealIntervalField or ComplexIntervalField of a given precision, then the answer will always be correct (or an exception will be raised, if a case is not implemented). Each root will be contained in one of the returned intervals, and the intervals will be disjoint. (The returned intervals may be of higher precision than the specified output ring.)
At the end of this docstring (after the examples) is a description of all the cases implemented in this function, and the algorithms used. That section also describes the possibilities for “algorithm=”, for the cases where multiple algorithms exist.
EXAMPLES:
sage: x = QQ['x'].0
sage: f = x^3 - 1
sage: f.roots()
[(1, 1)]
sage: f.roots(ring=CC) # note -- low order bits slightly different on ppc.
[(1.00000000000000, 1), (-0.500000000000000 - 0.86602540378443...*I, 1), (-0.500000000000000 + 0.86602540378443...*I, 1)]
sage: f = (x^3 - 1)^2
sage: f.roots()
[(1, 2)]
sage: f = -19*x + 884736
sage: f.roots()
[(884736/19, 1)]
sage: (f^20).roots()
[(884736/19, 20)]
sage: K.<z> = CyclotomicField(3)
sage: f = K.defining_polynomial()
sage: f.roots(ring=GF(7))
[(4, 1), (2, 1)]
sage: g = f.change_ring(GF(7))
sage: g.roots()
[(4, 1), (2, 1)]
sage: g.roots(multiplicities=False)
[4, 2]
An example over RR, which illustrates that only the roots in RR are returned:
sage: x = RR['x'].0
sage: f = x^3 -2
sage: f.roots()
[(1.25992104989487, 1)]
sage: f.factor()
(x - 1.25992104989487) * (x^2 + 1.25992104989487*x + 1.58740105196820)
sage: x = RealField(100)['x'].0
sage: f = x^3 -2
sage: f.roots()
[(1.2599210498948731647672106073, 1)]
sage: x = CC['x'].0
sage: f = x^3 -2
sage: f.roots()
[(1.25992104989487, 1), (-0.62996052494743... - 1.09112363597172*I, 1), (-0.62996052494743... + 1.09112363597172*I, 1)]
sage: f.roots(algorithm='pari')
[(1.25992104989487, 1), (-0.629960524947437 - 1.09112363597172*I, 1), (-0.629960524947437 + 1.09112363597172*I, 1)]
Another example showing that only roots in the base ring are returned:
sage: x = polygen(ZZ)
sage: f = (2*x-3) * (x-1) * (x+1)
sage: f.roots()
[(1, 1), (-1, 1)]
sage: f.roots(ring=QQ)
[(3/2, 1), (1, 1), (-1, 1)]
An example involving large numbers:
sage: x = RR['x'].0
sage: f = x^2 - 1e100
sage: f.roots()
[(-1.00000000000000e50, 1), (1.00000000000000e50, 1)]
sage: f = x^10 - 2*(5*x-1)^2
sage: f.roots(multiplicities=False)
[-1.6772670339941..., 0.19995479628..., 0.20004530611..., 1.5763035161844...]
sage: x = CC['x'].0
sage: i = CC.0
sage: f = (x - 1)*(x - i)
sage: f.roots(multiplicities=False) #random - this example is numerically rather unstable
[2.22044604925031e-16 + 1.00000000000000*I, 1.00000000000000 + 8.32667268468867e-17*I]
sage: g=(x-1.33+1.33*i)*(x-2.66-2.66*i)
sage: g.roots(multiplicities=False)
[1.33000000000000 - 1.33000000000000*I, 2.66000000000000 + 2.66000000000000*I]
A purely symbolic roots example:
sage: X = var('X')
sage: f = expand((X-1)*(X-I)^3*(X^2 - sqrt(2))); f
-sqrt(2)*X^4 + I*sqrt(2) + X^6 + (-3*I - 1)*X^5 + (3*I - 3)*X^4 + (3*I + 1)*sqrt(2)*X^3 + (I + 3)*X^3 + (-3*I + 3)*sqrt(2)*X^2 - I*X^2 + (-I - 3)*sqrt(2)*X
sage: print f.roots()
[(I, 3), (-2^(1/4), 1), (2^(1/4), 1), (1, 1)]
A couple of examples where the base ring doesn’t have a factorization algorithm (yet). Note that this is currently done via naive enumeration, so could be very slow:
sage: R = Integers(6)
sage: S.<x> = R['x']
sage: p = x^2-1
sage: p.roots()
...
NotImplementedError: root finding with multiplicities for this polynomial not implemented (try the multiplicities=False option)
sage: p.roots(multiplicities=False)
[1, 5]
sage: R = Integers(9)
sage: A = PolynomialRing(R, 'y')
sage: y = A.gen()
sage: f = 10*y^2 - y^3 - 9
sage: f.roots(multiplicities=False)
[0, 1, 3, 6]
An example over the complex double field (where root finding is fast, thanks to numpy):
sage: R.<x> = CDF[]
sage: f = R.cyclotomic_polynomial(5); f
x^4 + x^3 + x^2 + x + 1.0
sage: f.roots(multiplicities=False) # slightly random
[0.309016994375 + 0.951056516295*I, 0.309016994375 - 0.951056516295*I, -0.809016994375 + 0.587785252292*I, -0.809016994375 - 0.587785252292*I]
sage: [z^5 for z in f.roots(multiplicities=False)] # slightly random
[1.0 - 2.44929359829e-16*I, 1.0 + 2.44929359829e-16*I, 1.0 - 4.89858719659e-16*I, 1.0 + 4.89858719659e-16*I]
sage: f = CDF['x']([1,2,3,4]); f
4.0*x^3 + 3.0*x^2 + 2.0*x + 1.0
sage: r = f.roots(multiplicities=False)
sage: [f(a) for a in r] # slightly random
[2.55351295664e-15, -4.4408920985e-16 - 2.08166817117e-16*I, -4.4408920985e-16 + 2.08166817117e-16*I]
Another example over RDF:
sage: x = RDF['x'].0
sage: ((x^3 -1)).roots()
[(1.0, 1)]
sage: ((x^3 -1)).roots(multiplicities=False)
[1.0]
Another examples involving the complex double field:
sage: x = CDF['x'].0
sage: i = CDF.0
sage: f = x^3 + 2*i; f
x^3 + 2.0*I
sage: f.roots()
[(-1.09112363597 - 0.629960524947*I, 1),
(... + 1.25992104989*I, 1),
(1.09112363597 - 0.629960524947*I, 1)]
sage: f.roots(multiplicities=False)
[-1.09112363597 - 0.629960524947*I,
... + 1.25992104989r*I,
1.09112363597 - 0.629960524947*I]
sage: [f(z) for z in f.roots(multiplicities=False)] # random, too close to 0
[-2.56337823492e-15 - 6.66133814775e-15*I,
3.96533069372e-16 + 1.99840144433e-15*I,
4.19092485179e-17 - 8.881784197e-16*I]
sage: f = i*x^3 + 2; f
I*x^3 + 2.0
sage: f.roots()
[(-1.09112363597 + 0.629960524947*I, 1),
(... - 1.25992104989*I, 1),
(1.09112363597 + 0.629960524947*I, 1)]
sage: f(f.roots()[0][0]) # random, too close to 0
-2.56337823492e-15 - 6.66133814775e-15*I
Examples using real root isolation:
sage: x = polygen(ZZ)
sage: f = x^2 - x - 1
sage: f.roots()
[]
sage: f.roots(ring=RIF)
[(-0.6180339887498948482045868343657?, 1), (1.6180339887498948482045868343657?, 1)]
sage: f.roots(ring=RIF, multiplicities=False)
[-0.6180339887498948482045868343657?, 1.6180339887498948482045868343657?]
sage: f.roots(ring=RealIntervalField(150))
[(-0.6180339887498948482045868343656381177203091798057628621354486227?, 1), (1.618033988749894848204586834365638117720309179805762862135448623?, 1)]
sage: f.roots(ring=AA)
[(-0.618033988749895?, 1), (1.618033988749895?, 1)]
sage: f = f^2 * (x - 1)
sage: f.roots(ring=RIF)
[(-0.6180339887498948482045868343657?, 2), (1.0000000000000000000000000000000?, 1), (1.6180339887498948482045868343657?, 2)]
sage: f.roots(ring=RIF, multiplicities=False)
[-0.6180339887498948482045868343657?, 1.0000000000000000000000000000000?, 1.6180339887498948482045868343657?]
Examples using complex root isolation:
sage: x = polygen(ZZ)
sage: p = x^5 - x - 1
sage: p.roots()
[]
sage: p.roots(ring=CIF)
[(1.167303978261419?, 1), (-0.764884433600585? - 0.352471546031727?*I, 1), (-0.764884433600585? + 0.352471546031727?*I, 1), (0.181232444469876? - 1.083954101317711?*I, 1), (0.181232444469876? + 1.083954101317711?*I, 1)]
sage: p.roots(ring=ComplexIntervalField(200))
[(1.167303978261418684256045899854842180720560371525489039140082?, 1), (-0.76488443360058472602982318770854173032899665194736756700778? - 0.35247154603172624931794709140258105439420648082424733283770?*I, 1), (-0.76488443360058472602982318770854173032899665194736756700778? + 0.35247154603172624931794709140258105439420648082424733283770?*I, 1), (0.18123244446987538390180023778112063996871646618462304743774? - 1.08395410131771066843034449298076657427364024315511565430114?*I, 1), (0.18123244446987538390180023778112063996871646618462304743774? + 1.08395410131771066843034449298076657427364024315511565430114?*I, 1)]
sage: rts = p.roots(ring=QQbar); rts
[(1.167303978261419?, 1), (-0.7648844336005847? - 0.3524715460317263?*I, 1), (-0.7648844336005847? + 0.3524715460317263?*I, 1), (0.1812324444698754? - 1.083954101317711?*I, 1), (0.1812324444698754? + 1.083954101317711?*I, 1)]
sage: p.roots(ring=AA)
[(1.167303978261419?, 1)]
sage: p = (x - rts[4][0])^2 * (3*x^2 + x + 1)
sage: p.roots(ring=QQbar)
[(-0.1666666666666667? - 0.552770798392567?*I, 1), (-0.1666666666666667? + 0.552770798392567?*I, 1), (0.1812324444698754? + 1.083954101317711?*I, 2)]
sage: p.roots(ring=CIF)
[(-0.1666666666666667? - 0.552770798392567?*I, 1), (-0.1666666666666667? + 0.552770798392567?*I, 1), (0.1812324444698754? + 1.083954101317711?*I, 2)]
Note that coefficients in a number field with defining polynomial
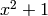 are considered to be Gaussian rationals (with the
generator mapping to +I), if you ask for complex roots.
are considered to be Gaussian rationals (with the
generator mapping to +I), if you ask for complex roots.
sage: K.<im> = NumberField(x^2 + 1)
sage: y = polygen(K)
sage: p = y^4 - 2 - im
sage: p.roots(ring=CC)
[(-1.2146389322441... - 0.14142505258239...*I, 1), (-0.14142505258239... + 1.2146389322441...*I, 1), (0.14142505258239... - 1.2146389322441...*I, 1), (1.2146389322441... + 0.14142505258239...*I, 1)]
sage: p = p^2 * (y^2 - 2)
sage: p.roots(ring=CIF)
[(-1.414213562373095?, 1), (1.414213562373095?, 1), (-1.214638932244183? - 0.141425052582394?*I, 2), (-0.141425052582394? + 1.214638932244183?*I, 2), (0.141425052582394? - 1.214638932244183?*I, 2), (1.214638932244183? + 0.141425052582394?*I, 2)]
There are many combinations of floating-point input and output types that work. (Note that some of them are quite pointless... there’s no reason to use high-precision input and output, and still use numpy to find the roots.)
sage: rflds = (RR, RDF, RealField(100))
sage: cflds = (CC, CDF, ComplexField(100))
sage: def cross(a, b):
... return list(cartesian_product_iterator([a, b]))
sage: flds = cross(rflds, rflds) + cross(rflds, cflds) + cross(cflds, cflds)
sage: for (fld_in, fld_out) in flds:
... x = polygen(fld_in)
... f = x^3 - fld_in(2)
... x2 = polygen(fld_out)
... f2 = x2^3 - fld_out(2)
... for algo in (None, 'pari', 'numpy'):
... rts = f.roots(ring=fld_out, multiplicities=False)
... if fld_in == fld_out and algo is None:
... print fld_in, rts
... for rt in rts:
... assert(abs(f2(rt)) <= 1e-10)
... assert(rt.parent() == fld_out)
Real Field with 53 bits of precision [1.25992104989487]
Real Double Field [1.25992104989]
Real Field with 100 bits of precision [1.2599210498948731647672106073]
Complex Field with 53 bits of precision [1.25992104989487, -0.62996052494743... - 1.09112363597172*I, -0.62996052494743... + 1.09112363597172*I]
Complex Double Field [1.25992104989, -0.62996052494... - 1.09112363597*I, -0.62996052494... + 1.09112363597*I]
Complex Field with 100 bits of precision [1.2599210498948731647672106073, -0.62996052494743658238360530364 - 1.0911236359717214035600726142*I, -0.62996052494743658238360530364 + 1.0911236359717214035600726142*I]
Note that we can find the roots of a polynomial with algebraic coefficients:
sage: rt2 = sqrt(AA(2))
sage: rt3 = sqrt(AA(3))
sage: x = polygen(AA)
sage: f = (x - rt2) * (x - rt3); f
x^2 - 3.146264369941973?*x + 2.449489742783178?
sage: rts = f.roots(); rts
[(1.414213562373095?, 1), (1.732050807568878?, 1)]
sage: rts[0][0] == rt2
True
sage: f.roots(ring=RealIntervalField(150))
[(1.414213562373095048801688724209698078569671875376948073176679738?, 1), (1.732050807568877293527446341505872366942805253810380628055806980?, 1)]
We can handle polynomials with huge coefficients.
This number doesn’t even fit in an IEEE double-precision float, but RR and CC allow a much larger range of floating-point numbers:
sage: bigc = 2^1500
sage: CDF(bigc)
+infinity
sage: CC(bigc)
3.50746621104340e451
Polynomials using such large coefficients can’t be handled by numpy, but pari can deal with them:
sage: x = polygen(QQ)
sage: p = x + bigc
sage: p.roots(ring=RR, algorithm='numpy')
...
LinAlgError: Array must not contain infs or NaNs
sage: p.roots(ring=RR, algorithm='pari')
[(-3.50746621104340e451, 1)]
sage: p.roots(ring=AA)
[(-3.5074662110434039?e451, 1)]
sage: p.roots(ring=QQbar)
[(-3.5074662110434039?e451, 1)]
sage: p = bigc*x + 1
sage: p.roots(ring=RR)
[(0.000000000000000, 1)]
sage: p.roots(ring=AA)
[(-2.8510609648967059?e-452, 1)]
sage: p.roots(ring=QQbar)
[(-2.8510609648967059?e-452, 1)]
sage: p = x^2 - bigc
sage: p.roots(ring=RR)
[(-5.92238652153286e225, 1), (5.92238652153286e225, 1)]
sage: p.roots(ring=QQbar)
[(-5.9223865215328558?e225, 1), (5.9223865215328558?e225, 1)]
Algorithms used:
For brevity, we will use RR to mean any RealField of any precision;
similarly for RIF, CC, and CIF. Since Sage has no specific
implementation of Gaussian rationals (or of number fields with
embedding, at all), when we refer to Gaussian rationals below we
will accept any number field with defining polynomial
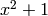 , mapping the field generator to +I.
, mapping the field generator to +I.
We call the base ring of the polynomial K, and the ring given by the ring= argument L. (If ring= is not specified, then L is the same as K.)
If K and L are floating-point (RDF, CDF, RR, or CC), then a floating-point root-finder is used. If L is RDF or CDF then we default to using NumPy’s roots(); otherwise, we use Pari’s polroots(). This choice can be overridden with algorithm=’pari’ or algorithm=’numpy’. If the algorithm is unspecified and NumPy’s roots() algorithm fails, then we fall back to pari (numpy will fail if some coefficient is infinite, for instance).
If L is AA or RIF, and K is ZZ, QQ, or AA, then the root isolation algorithm sage.rings.polynomial.real_roots.real_roots() is used. (You can call real_roots() directly to get more control than this method gives.)
If L is QQbar or CIF, and K is ZZ, QQ, AA, QQbar, or the Gaussian rationals, then the root isolation algorithm sage.rings.polynomial.complex_roots.complex_roots() is used. (You can call complex_roots() directly to get more control than this method gives.)
If L is AA and K is QQbar or the Gaussian rationals, then complex_roots() is used (as above) to find roots in QQbar, then these roots are filtered to select only the real roots.
If L is floating-point and K is not, then we attempt to change the polynomial ring to L (using .change_ring()) (or, if L is complex and K is not, to the corresponding real field). Then we use either Pari or numpy as specified above.
For all other cases where K is different than L, we just use .change_ring(L) and proceed as below.
The next method, which is used if K is an integral domain, is to attempt to factor the polynomial. If this succeeds, then for every degree-one factor a*x+b, we add -b/a as a root (as long as this quotient is actually in the desired ring).
If factoring over K is not implemented (or K is not an integral domain), and K is finite, then we find the roots by enumerating all elements of K and checking whether the polynomial evaluates to zero at that value.
Note
We mentioned above that polynomials with multiple roots are always ill-conditioned; if your input is given to n bits of precision, you should not expect more than n/k good bits for a k-fold root. (You can get solutions that make the polynomial evaluate to a number very close to zero; basically the problem is that with a multiple root, there are many such numbers, and it’s difficult to choose between them.)
To see why this is true, consider the naive floating-point
error analysis model where you just pretend that all
floating-point numbers are somewhat imprecise - a little
‘fuzzy’, if you will. Then the graph of a floating-point
polynomial will be a fuzzy line. Consider the graph of
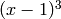 ; this will be a fuzzy line with a
horizontal tangent at
; this will be a fuzzy line with a
horizontal tangent at 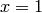 ,
, 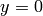 . If the
fuzziness extends up and down by about j, then it will
extend left and right by about cube_root(j).
. If the
fuzziness extends up and down by about j, then it will
extend left and right by about cube_root(j).
TESTS:
sage: K.<zeta> = CyclotomicField(2)
sage: R.<x> = K[]
sage: factor(x^3-1)
(x - 1) * (x^2 + x + 1)
This shows that the issue from trac ticket #6237 is fixed:
sage: R.<u> = QQ[]
sage: g = -27*u^14 - 32*u^9
sage: g.roots(CDF, multiplicities=False)
[-1.03456371594, 0, -0.31969776999 - 0.983928563571*I, -0.31969776999 + 0.983928563571*I, 0.836979627962 - 0.608101294789*I, 0.836979627962 + 0.608101294789*I]
sage: g.roots(CDF)
[(-1.03456371594, 1), (0, 9), (-0.31969776999 - 0.983928563571*I, 1), (-0.31969776999 + 0.983928563571*I, 1), (0.836979627962 - 0.608101294789*I, 1), (0.836979627962 + 0.608101294789*I, 1)]
This shows that the issue at trac ticket #2418 is fixed:
sage: x = polygen(QQ)
sage: p = (x^50/2^100 + x^10 + x + 1).change_ring(ComplexField(106))
sage: rts = (p/2^100).roots(multiplicities=False)
sage: eps = 2^(-50) # we test the roots numerically
sage: [abs(p(rt)) < eps for rt in rts] == [True]*50
True
Returns this polynomial multiplied by the power 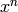 . If
. If
 is negative, terms below
is negative, terms below 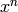 will be
discarded. Does not change this polynomial (since polynomials are
immutable).
will be
discarded. Does not change this polynomial (since polynomials are
immutable).
EXAMPLES:
sage: R.<x> = QQ[]
sage: p = x^2 + 2*x + 4
sage: p.shift(0)
x^2 + 2*x + 4
sage: p.shift(-1)
x + 2
sage: p.shift(-5)
0
sage: p.shift(2)
x^4 + 2*x^3 + 4*x^2
One can also use the infix shift operator:
sage: f = x^3 + x
sage: f >> 2
x
sage: f << 2
x^5 + x^3
TESTS:
sage: p = R(0)
sage: p.shift(3).is_zero()
True
sage: p.shift(-3).is_zero()
True
AUTHORS:
Returns the square of this polynomial.
TODO:
AUTHORS:
EXAMPLES:
sage: R.<x> = QQ[]
sage: f = x^3 + 1
sage: f.square()
x^6 + 2*x^3 + 1
sage: f*f
x^6 + 2*x^3 + 1
Return the square-free decomposition of self. This is a partial factorization of self into square-free, relatively prime polynomials.
This is the straightforward algorithm, using only polynomial GCD and polynomial division. Faster algorithms exist. The algorithm comes from the Wikipedia article, “Square-free polynomial”.
EXAMPLES:
sage: x = polygen(QQ)
sage: p = 37 * (x-1)^3 * (x-2)^3 * (x-1/3)^7 * (x-3/7)
sage: p.squarefree_decomposition()
(37*x - 111/7) * (x^2 - 3*x + 2)^3 * (x - 1/3)^7
sage: p = 37 * (x-2/3)^2
sage: p.squarefree_decomposition()
(37) * (x - 2/3)^2
sage: x = polygen(GF(3))
sage: x.squarefree_decomposition()
x
sage: f = QQbar['x'](1)
sage: f.squarefree_decomposition()
1
Identical to self(*x).
See the docstring for self.__call__.
EXAMPLES:
sage: R.<x> = QQ[]
sage: f = x^3 + x - 3
sage: f.subs(x=5)
127
sage: f.subs(5)
127
sage: f.subs({x:2})
7
sage: f.subs({})
x^3 + x - 3
sage: f.subs({'x':2})
...
TypeError: keys do not match self's parent
Identical to self(*x).
See the docstring for self.__call__.
EXAMPLES:
sage: R.<x> = QQ[]
sage: f = x^3 + x - 3
sage: f.subs(x=5)
127
sage: f.subs(5)
127
sage: f.subs({x:2})
7
sage: f.subs({})
x^3 + x - 3
sage: f.subs({'x':2})
...
TypeError: keys do not match self's parent
Returns the polynomial of degree ` < n` which is equivalent
to self modulo 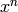 .
.
EXAMPLES:
sage: R.<x> = ZZ[]; S.<y> = R[]
sage: f = y^3 + x*y -3*x; f
y^3 + x*y - 3*x
sage: f.truncate(2)
x*y - 3*x
sage: f.truncate(1)
-3*x
sage: f.truncate(0)
0
If 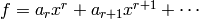 , with
, with
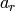 nonzero, then the valuation of
nonzero, then the valuation of  is
is
 . The valuation of the zero polynomial is
. The valuation of the zero polynomial is
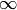 .
.
If a prime (or non-prime)  is given, then the valuation
is the largest power of
is given, then the valuation
is the largest power of  which divides self.
which divides self.
The valuation at 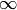 is -self.degree().
is -self.degree().
EXAMPLES:
sage: P,x=PolynomialRing(ZZ,'x').objgen()
sage: (x^2+x).valuation()
1
sage: (x^2+x).valuation(x+1)
1
sage: (x^2+1).valuation()
0
sage: (x^3+1).valuation(infinity)
-3
sage: P(0).valuation()
+Infinity
Return name of variable used in this polynomial as a string.
OUTPUT: string
EXAMPLES:
sage: R.<t> = QQ[]
sage: f = t^3 + 3/2*t + 5
sage: f.variable_name()
't'
Returns the tuple of variables occurring in this polynomial.
EXAMPLES:
sage: R.<x> = QQ[]
sage: x.variables()
(x,)
A constant polynomial has no variables.
sage: R(2).variables()
()
Bases: sage.categories.morphism.Morphism
This class is used for conversion from a ring to a polynomial over that ring.
It calls the _new_constant_poly method on the generator, which should be optimized for a particular polynomial type. Technically, it should be a method of the polynomial ring, but few polynomial rings are cython classes.
TESTS:
sage: from sage.rings.polynomial.polynomial_element import PolynomialBaseringInjection
sage: m = PolynomialBaseringInjection(RDF, RDF['x'])
sage: m.section()
Generic map:
From: Univariate Polynomial Ring in x over Real Double Field
To: Real Double Field
sage: type(m.section())
<type 'sage.rings.polynomial.polynomial_element.ConstantPolynomialSection'>
Bases: sage.rings.polynomial.polynomial_element.Polynomial
A generic dense polynomial.
EXAMPLES:
sage: R.<x> = PolynomialRing(PolynomialRing(QQ,'y'))
sage: f = x^3 - x + 17
sage: type(f)
<type 'sage.rings.polynomial.polynomial_element.Polynomial_generic_dense'>
sage: loads(f.dumps()) == f
True
Return the constant coefficient of this polynomial.
EXAMPLES:
sage: R.<x> = RDF[]
sage: f = (1+2*x^7)^5
sage: f.degree()
35
Return a new copy of the list of the underlying elements of self.
EXAMPLES:
sage: R.<x> = GF(17)[]
sage: f = (1+2*x)^3 + 3*x; f
8*x^3 + 12*x^2 + 9*x + 1
sage: f.list()
[1, 9, 12, 8]
Returns this polynomial multiplied by the power 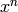 . If
. If
 is negative, terms below
is negative, terms below 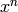 will be
discarded. Does not change this polynomial.
will be
discarded. Does not change this polynomial.
EXAMPLES:
sage: R.<x> = PolynomialRing(PolynomialRing(QQ,'y'), 'x')
sage: p = x^2 + 2*x + 4
sage: type(p)
<type 'sage.rings.polynomial.polynomial_element.Polynomial_generic_dense'>
sage: p.shift(0)
x^2 + 2*x + 4
sage: p.shift(-1)
x + 2
sage: p.shift(2)
x^4 + 2*x^3 + 4*x^2
TESTS:
sage: p = R(0)
sage: p.shift(3).is_zero()
True
sage: p.shift(-3).is_zero()
True
AUTHORS:
Returns the polynomial of degree ` < n` which is equivalent
to self modulo 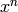 .
.
EXAMPLES:
sage: S.<q> = QQ['t']['q']
sage: f = (1+q^10+q^11+q^12).truncate(11); f
q^10 + 1
sage: f = (1+q^10+q^100).truncate(50); f
q^10 + 1
sage: f.degree()
10
sage: f = (1+q^10+q^100).truncate(500); f
q^100 + q^10 + 1
TESTS:
Make sure we’re not actually testing a specialized implementation.
sage: type(f)
<type 'sage.rings.polynomial.polynomial_element.Polynomial_generic_dense'>
Return True if f is of type univariate polynomial.
INPUT:
EXAMPLES:
sage: from sage.rings.polynomial.polynomial_element import is_Polynomial
sage: R.<x> = ZZ[]
sage: is_Polynomial(x^3 + x + 1)
True
sage: S.<y> = R[]
sage: f = y^3 + x*y -3*x; f
y^3 + x*y - 3*x
sage: is_Polynomial(f)
True
However this function does not return True for genuine multivariate polynomial type objects or symbolic polynomials, since those are not of the same data type as univariate polynomials:
sage: R.<x,y> = QQ[]
sage: f = y^3 + x*y -3*x; f
y^3 + x*y - 3*x
sage: is_Polynomial(f)
False
sage: var('x,y')
(x, y)
sage: f = y^3 + x*y -3*x; f
y^3 + x*y - 3*x
sage: is_Polynomial(f)
False