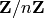Dense univariate polynomials over , implemented using FLINT.

This module gives a fast implementation of whenever is at most sys.maxint. We use it by default in preference to NTL when the modulus is small, falling back to NTL if the modulus is too large, as in the example below.

EXAMPLES:

sage: R.<a> = PolynomialRing(Integers(100))
sage: type(a)
<type 'sage.rings.polynomial.polynomial_zmod_flint.Polynomial_zmod_flint'>
sage: R.<a> = PolynomialRing(Integers(5*2^64))
sage: type(a)
<type 'sage.rings.polynomial.polynomial_modn_dense_ntl.Polynomial_dense_modn_ntl_ZZ'>
sage: R.<a> = PolynomialRing(Integers(5*2^64), implementation="FLINT")
...
ValueError: FLINT does not support modulus 92233720368547758080

AUTHORS:

• Burcin Erocal (2008-11) initial implementation
• Martin Albrecht (2009-01) another initial implementation

class sage.rings.polynomial.polynomial_zmod_flint.Polynomial_template

Bases: sage.rings.polynomial.polynomial_element.Polynomial

Template for interfacing to external C / C++ libraries for implementations of polynomials.

AUTHORS:

• Robert Bradshaw (2008-10): original idea for templating
• Martin Albrecht (2008-10): initial implementation

This file implements a simple templating engine for linking univariate polynomials to their C/C++ library implementations. It requires a ‘linkage’ file which implements the celement_ functions (see sage.libs.ntl.ntl_GF2X_linkage for an example). Both parts are then plugged together by inclusion of the linkage file when inheriting from this class. See sage.rings.polynomial.polynomial_gf2x for an example.

We illustrate the generic glueing using univariate polynomials over .

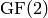Note

Implementations using this template MUST implement coercion from base ring elements and __getitem__. See Polynomial_GF2X for an example.

degree()

EXAMPLE:

sage: P.<x> = GF(2)[]
sage: x.degree()
1
sage: P(1).degree()
0
sage: P(0).degree()
-1

gcd(other)

Return the greatest common divisor of self and other.

EXAMPLE:

sage: P.<x> = GF(2)[]
sage: f = x*(x+1)
sage: f.gcd(x+1)
x + 1
sage: f.gcd(x^2)
x

is_gen()

EXAMPLE:

sage: P.<x> = GF(2)[]
sage: x.is_gen()
True
sage: (x+1).is_gen()
False

is_one()

EXAMPLE:

sage: P.<x> = GF(2)[]
sage: P(1).is_one()
True

is_zero()

EXAMPLE:

sage: P.<x> = GF(2)[]
sage: x.is_zero()
False

list()

EXAMPLE:

sage: P.<x> = GF(2)[]
sage: x.list()
[0, 1]
sage: list(x)
[0, 1]

quo_rem(right)

EXAMPLE:

sage: P.<x> = GF(2)[]
sage: f = x^2 + x + 1
sage: f.quo_rem(x + 1)
(x, 1)

shift(n)

EXAMPLE:

sage: P.<x> = GF(2)[]
sage: f = x^3 + x^2 + 1
sage: f.shift(1)
x^4 + x^3 + x
sage: f.shift(-1)
x^2 + x

truncate(n)

Returns this polynomial mod .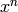

EXAMPLES:

sage: R.<x> =GF(2)[]
sage: f = sum(x^n for n in range(10)); f
x^9 + x^8 + x^7 + x^6 + x^5 + x^4 + x^3 + x^2 + x + 1
sage: f.truncate(6)
x^5 + x^4 + x^3 + x^2 + x + 1

xgcd(other)

Computes extended gcd of self and other.

EXAMPLE:

sage: P.<x> = GF(7)[]
sage: f = x*(x+1)
sage: f.xgcd(x+1)
(x + 1, 0, 1)
sage: f.xgcd(x^2)
(x, 1, 6)

class sage.rings.polynomial.polynomial_zmod_flint.Polynomial_zmod_flint

Bases: sage.rings.polynomial.polynomial_zmod_flint.Polynomial_template

factor()

Returns the factorization of the polynomial.

EXAMPLES:

sage: R.<x> = GF(5)[]
sage: (x^2 + 1).factor()
(x + 2) * (x + 3)

TESTS:

sage: (2*x^2 + 2).factor()
(2) * (x + 2) * (x + 3)
sage: P.<x> = Zmod(10)[]
sage: (x^2).factor()
...
NotImplementedError: factorization of polynomials over rings with composite characteristic is not implemented

is_irreducible()

Return True if this polynomial is irreducible.

EXAMPLES:

sage: R.<x> = GF(5)[]
sage: (x^2 + 1).is_irreducible()
False
sage: (x^3 + x + 1).is_irreducible()
True

TESTS:

sage: R(0).is_irreducible()
...
ValueError: must be nonzero
sage: R(1).is_irreducible()
False
sage: R(2).is_irreducible()
False

sage: S.<s> = Zmod(10)[]
sage: (s^2).is_irreducible()
...
NotImplementedError: checking irreducibility of polynomials over rings with composite characteristic is not implemented
sage: S(1).is_irreducible()
False
sage: S(2).is_irreducible()
...
NotImplementedError: checking irreducibility of polynomials over rings with composite characteristic is not implemented

monic()

Return this polynomial divided by its leading coefficient.

Raises ValueError if the leading cofficient is not invertible in the base ring.

EXAMPLES:

sage: R.<x> = GF(5)[]
sage: (2*x^2+1).monic()
x^2 + 3

TESTS:

sage: R.<x> = Zmod(10)[]
sage: (5*x).monic()
...
ValueError: leading coefficient must be invertible

rational_reconstruct(m, n_deg=0, d_deg=0)

Construct a rational function n/d such that 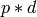is equivalent to modulo where is this polynomial.

EXAMPLES:

sage: P.<x> = GF(5)[]
sage: p = 4*x^5 + 3*x^4 + 2*x^3 + 2*x^2 + 4*x + 2
sage: n, d = p.rational_reconstruct(x^9, 4, 4); n, d
(3*x^4 + 2*x^3 + x^2 + 2*x, x^4 + 3*x^3 + x^2 + x)
sage: (p*d % x^9) == n
True

resultant(other)

A decorator to be used on binary operation methods that should operate on elements of the same parent. If the parents of the arguments differ, coercion is performed, then the method is re-looked up by name on the first argument.

In short, using the NamedBinopMethod (alias coerce_binop) decorator on a method gives it the exact same semantics of the basic arithmetic operations like _add_, _sub_, etc. in that both operands are guaranteed to have exactly the same parent.

reverse(degree=None)

Return a polynomial with the coefficients of this polynomial reversed.

If an optional degree argument is given the coefficient list will be truncated or zero padded as necessary and the reverse polynomial will have the specified degree.

EXAMPLES:

sage: R.<x> = GF(5)[]
sage: p = R([1,2,3,4]); p
4*x^3 + 3*x^2 + 2*x + 1
sage: p.reverse()
x^3 + 2*x^2 + 3*x + 4
sage: p.reverse(degree=6)
x^6 + 2*x^5 + 3*x^4 + 4*x^3
sage: p.reverse(degree=2)
x^2 + 2*x + 3

TESTS:

sage: p.reverse(degree=1.5r)
...
ValueError: degree argument must be a non-negative integer, got 1.5

small_roots(*args, **kwds)

See sage.rings.polynomial.polynomial_modn_dense_ntl.small_roots() for the documentation of this function.

EXAMPLE:

sage: N = 10001
sage: K = Zmod(10001)
sage: P.<x> = PolynomialRing(K)
sage: f = x^3 + 10*x^2 + 5000*x - 222
sage: f.small_roots()
[4]

squarefree_decomposition()

Returns the squarefree decomposition of this polynomial.

EXAMPLES:

sage: R.<x> = GF(5)[]
sage: ((x+1)*(x^2+1)^2*x^3).squarefree_decomposition()
(x + 1) * (x^2 + 1)^2 * x^3

TESTS:

sage: (2*x*(x+1)^2).squarefree_decomposition()
(2) * x * (x + 1)^2
sage: P.<x> = Zmod(10)[]
sage: (x^2).squarefree_decomposition()
...
NotImplementedError: square free factorization of polynomials over rings with composite characteristic is not implemented

sage.rings.polynomial.polynomial_zmod_flint.make_element(parent, args)