AUTHORS:
EXAMPLES:
sage: a = matrix(ZZ, 3,3, range(9)); a
[0 1 2]
[3 4 5]
[6 7 8]
sage: a.det()
0
sage: a[0,0] = 10; a.det()
-30
sage: a.charpoly()
x^3 - 22*x^2 + 102*x + 30
sage: b = -3*a
sage: a == b
False
sage: b < a
True
TESTS:
sage: a = matrix(ZZ,2,range(4), sparse=False)
sage: TestSuite(a).run()
sage: Matrix(ZZ,0,0).inverse()
[]
Bases: sage.matrix.matrix_dense.Matrix_dense
Matrix over the integers.
On a 32-bit machine, they can have at most 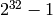 rows or
columns. On a 64-bit machine, matrices can have at most
rows or
columns. On a 64-bit machine, matrices can have at most
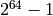 rows or columns.
rows or columns.
EXAMPLES:
sage: a = MatrixSpace(ZZ,3)(2); a
[2 0 0]
[0 2 0]
[0 0 2]
sage: a = matrix(ZZ,1,3, [1,2,-3]); a
[ 1 2 -3]
sage: a = MatrixSpace(ZZ,2,4)(2); a
...
TypeError: nonzero scalar matrix must be square
Block Korkin-Zolotarev reduction.
INPUT:
EXAMPLE:
sage: A = Matrix(ZZ,3,3,range(1,10))
sage: A.BKZ()
[ 0 0 0]
[ 2 1 0]
[-1 1 3]
sage: A = Matrix(ZZ,3,3,range(1,10))
sage: A.BKZ(use_givens=True)
[ 0 0 0]
[ 2 1 0]
[-1 1 3]
sage: A = Matrix(ZZ,3,3,range(1,10))
sage: A.BKZ(fp="fp")
[ 0 0 0]
[ 2 1 0]
[-1 1 3]
Returns LLL reduced or approximated LLL reduced lattice R for this matrix interpreted as a lattice.
A lattice 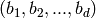 is
is
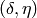 -LLL-reduced if the two following
conditions hold:
-LLL-reduced if the two following
conditions hold:
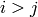 , we have
, we have 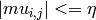 ,
,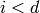 , we have
, we have
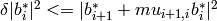 ,
,where 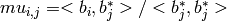 and
and
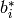 is the
is the  -th vector of the Gram-Schmidt
orthogonalisation of
-th vector of the Gram-Schmidt
orthogonalisation of 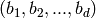 .
.
The default reduction parameters are 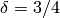 and
and
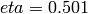 . The parameters
. The parameters 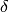 and
and
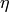 must satisfy:
must satisfy: 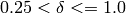 and
and
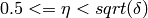 . Polynomial time
complexity is only guaranteed for
. Polynomial time
complexity is only guaranteed for 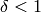 .
.
The lattice is returned as a matrix. Also the rank (and the determinant) of self are cached if those are computed during the reduction. Note that in general this only happens when self.rank() == self.ncols() and the exact algorithm is used.
INPUT:
delta - parameter as described above (default: 3/4)
eta - parameter as described above (default: 0.501), ignored by NTL
algorithm - string (default: “fpLLL:wrapper”) one of the algorithms mentioned below
fp
- None - NTL’s exact reduction or fpLLL’s wrapper
- 'fp' - double precision: NTL’s FP or fpLLL’s double
- 'qd' - quad doubles: NTL’s QP
- 'xd' - extended exponent: NTL’s XD or fpLLL’s dpe
- 'rr' - arbitrary precision: NTL’RR or fpLLL’s MPFR
prec - precision, ignored by NTL (default: auto choose)
early_red - perform early reduction, ignored by NTL (default: False)
use_givens - use Givens orthogonalization (default: False) only applicable to approximate reductions and NTL. This is more stable but slower.
Also, if the verbose level is = 2, some more verbose output is printed during the calculation if NTL is used.
AVAILABLE ALGORITHMS:
NTL:LLL - NTL’s LLL + fp
fpLLL:heuristic - fpLLL’s heuristic + fp
fpLLL:fast - fpLLL’s fast
fpLLL:wrapper - fpLLL’s automatic choice (default)
OUTPUT: a matrix over the integers
EXAMPLE:
sage: A = Matrix(ZZ,3,3,range(1,10))
sage: A.LLL()
[ 0 0 0]
[ 2 1 0]
[-1 1 3]
We compute the extended GCD of a list of integers using LLL, this example is from the Magma handbook:
sage: Q = [ 67015143, 248934363018, 109210, 25590011055, 74631449, \
10230248, 709487, 68965012139, 972065, 864972271 ]
sage: n = len(Q)
sage: S = 100
sage: X = Matrix(ZZ, n, n + 1)
sage: for i in xrange(n):
... X[i,i + 1] = 1
sage: for i in xrange(n):
... X[i,0] = S*Q[i]
sage: L = X.LLL()
sage: M = L.row(n-1).list()[1:]
sage: M
[-3, -1, 13, -1, -4, 2, 3, 4, 5, -1]
sage: add([Q[i]*M[i] for i in range(n)])
-1
ALGORITHM: Uses the NTL library by Victor Shoup or fpLLL library by Damien Stehle depending on the chosen algorithm.
REFERENCES:
LLL reduction of the lattice whose gram matrix is self.
INPUT:
OUTPUT:
ALGORITHM: Use PARI
EXAMPLES:
sage: M = Matrix(ZZ, 2, 2, [5,3,3,2]) ; M
[5 3]
[3 2]
sage: U = M.LLL_gram(); U
[-1 1]
[ 1 -2]
sage: U.transpose() * M * U
[1 0]
[0 1]
Semidefinite and indefinite forms raise a ValueError:
sage: Matrix(ZZ,2,2,[2,6,6,3]).LLL_gram()
...
ValueError: not a definite matrix
sage: Matrix(ZZ,2,2,[1,0,0,-1]).LLL_gram()
...
ValueError: not a definite matrix
BUGS: should work for semidefinite forms (PARI is ok)
Returns the antitranspose of self, without changing self.
EXAMPLES:
sage: A = matrix(2,3,range(6))
sage: type(A)
<type 'sage.matrix.matrix_integer_dense.Matrix_integer_dense'>
sage: A.antitranspose()
[5 2]
[4 1]
[3 0]
sage: A
[0 1 2]
[3 4 5]
sage: A.subdivide(1,2); A
[0 1|2]
[---+-]
[3 4|5]
sage: A.antitranspose()
[5|2]
[-+-]
[4|1]
[3|0]
INPUT:
Note
Linbox charpoly disabled on 64-bit machines, since it hangs in many cases.
EXAMPLES:
sage: A = matrix(ZZ,6, range(36))
sage: f = A.charpoly(); f
x^6 - 105*x^5 - 630*x^4
sage: f(A) == 0
True
sage: n=20; A = Mat(ZZ,n)(range(n^2))
sage: A.charpoly()
x^20 - 3990*x^19 - 266000*x^18
sage: A.minpoly()
x^3 - 3990*x^2 - 266000*x
Returns the decomposition of the free module on which this matrix A acts from the right (i.e., the action is x goes to x A), along with whether this matrix acts irreducibly on each factor. The factors are guaranteed to be sorted in the same way as the corresponding factors of the characteristic polynomial, and are saturated as ZZ modules.
INPUT:
EXAMPLES:
sage: t = ModularSymbols(11,sign=1).hecke_matrix(2)
sage: w = t.change_ring(ZZ)
sage: w.list()
[3, -1, 0, -2]
Return the determinant of this matrix.
INPUT:
algorithm
otherwise, use ‘padic’
'padic' - uses a p-adic / multimodular algorithm that relies on code in IML and linbox
'linbox' - calls linbox det (you must set proof=False to use this!)
'ntl' - calls NTL’s det function
'pari' - uses PARI
proof - bool or None; if None use proof.linear_algebra(); only relevant for the padic algorithm.
Note
It would be VERY VERY hard for det to fail even with proof=False.
stabilize - if proof is False, require det to be the same for this many CRT primes in a row. Ignored if proof is True.
ALGORITHM: The p-adic algorithm works by first finding a random
vector v, then solving A*x = v and taking the denominator
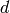 . This gives a divisor of the determinant. Then we
compute
. This gives a divisor of the determinant. Then we
compute 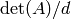 using a multimodular algorithm and the
Hadamard bound, skipping primes that divide
using a multimodular algorithm and the
Hadamard bound, skipping primes that divide 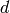 .
.
TIMINGS: This is perhaps the fastest implementation of determinants in the world. E.g., for a 500x500 random matrix with 32-bit entries on a core2 duo 2.6Ghz running OS X, Sage takes 4.12 seconds, whereas Magma takes 62.87 seconds (both with proof False). With proof=True on the same problem Sage takes 5.73 seconds. For another example, a 200x200 random matrix with 1-digit entries takes 4.18 seconds in pari, 0.18 in Sage with proof True, 0.11 in Sage with proof False, and 0.21 seconds in Magma with proof True and 0.18 in Magma with proof False.
EXAMPLES:
sage: A = matrix(ZZ,8,8,[3..66])
sage: A.determinant()
0
sage: A = random_matrix(ZZ,20,20)
sage: D1 = A.determinant()
sage: A._clear_cache()
sage: D2 = A.determinant(algorithm='ntl')
sage: D1 == D2
True
Next we try the Linbox det. Note that we must have proof=False.
sage: A = matrix(ZZ,5,[1,2,3,4,5,4,6,3,2,1,7,9,7,5,2,1,4,6,7,8,3,2,4,6,7])
sage: A.determinant(algorithm='linbox')
...
RuntimeError: you must pass the proof=False option to the determinant command to use LinBox's det algorithm
sage: A.determinant(algorithm='linbox',proof=False)
-21
sage: A._clear_cache()
sage: A.determinant()
-21
A bigger example:
sage: A = random_matrix(ZZ,30)
sage: d = A.determinant()
sage: A._clear_cache()
sage: A.determinant(algorithm='linbox',proof=False) == d
True
Return the echelon form of this matrix over the integers, also known as the hermit normal form (HNF).
INPUT:
algorithm
max 75 rows or columns: pari with flag 1 larger – use padic algorithm
If your matrix has large coefficients and is small, you may also want to try this.
'pari' - use PARI with flag 1
'pari0' - use PARI with flag 0
'pari4' - use PARI with flag 4 (use heuristic LLL)
full rank!)
proof - (default: True); if proof=False certain determinants are computed using a randomized hybrid p-adic multimodular strategy until it stabilizes twice (instead of up to the Hadamard bound). It is incredibly unlikely that one would ever get an incorrect result with proof=False.
include_zero_rows - (default: True) if False, don’t include zero rows
transformation - if given, also compute transformation matrix; only valid for padic algorithm
D - (default: None) if given and the algorithm is ‘ntl’, then D must be a multiple of the determinant and this function will use that fact.
OUTPUT:
Note
The result is not cached.
EXAMPLES:
sage: A = MatrixSpace(ZZ,2)([1,2,3,4])
sage: A.echelon_form()
[1 0]
[0 2]
sage: A = MatrixSpace(ZZ,5)(range(25))
sage: A.echelon_form()
[ 5 0 -5 -10 -15]
[ 0 1 2 3 4]
[ 0 0 0 0 0]
[ 0 0 0 0 0]
[ 0 0 0 0 0]
Getting a transformation matrix in the nonsquare case:
sage: A = matrix(ZZ,5,3,[1..15])
sage: H, U = A.hermite_form(transformation=True, include_zero_rows=False)
sage: H
[1 2 3]
[0 3 6]
sage: U
[ 0 0 0 4 -3]
[ 0 0 0 13 -10]
sage: U*A == H
True
TESTS: Make sure the zero matrices are handled correctly:
sage: m = matrix(ZZ,3,3,[0]*9)
sage: m.echelon_form()
[0 0 0]
[0 0 0]
[0 0 0]
sage: m = matrix(ZZ,3,1,[0]*3)
sage: m.echelon_form()
[0]
[0]
[0]
sage: m = matrix(ZZ,1,3,[0]*3)
sage: m.echelon_form()
[0 0 0]
The ultimate border case!
sage: m = matrix(ZZ,0,0,[])
sage: m.echelon_form()
[]
Note
If ‘ntl’ is chosen for a non square matrix this function raises a ValueError.
Special cases: 0 or 1 rows:
sage: a = matrix(ZZ, 1,2,[0,-1])
sage: a.hermite_form()
[0 1]
sage: a.pivots()
[1]
sage: a = matrix(ZZ, 1,2,[0,0])
sage: a.hermite_form()
[0 0]
sage: a.pivots()
[]
sage: a = matrix(ZZ,1,3); a
[0 0 0]
sage: a.echelon_form(include_zero_rows=False)
[]
sage: a.echelon_form(include_zero_rows=True)
[0 0 0]
Illustrate using various algorithms.:
sage: matrix(ZZ,3,[1..9]).hermite_form(algorithm='pari')
[1 2 3]
[0 3 6]
[0 0 0]
sage: matrix(ZZ,3,[1..9]).hermite_form(algorithm='pari0')
[1 2 3]
[0 3 6]
[0 0 0]
sage: matrix(ZZ,3,[1..9]).hermite_form(algorithm='pari4')
[1 2 3]
[0 3 6]
[0 0 0]
sage: matrix(ZZ,3,[1..9]).hermite_form(algorithm='padic')
[1 2 3]
[0 3 6]
[0 0 0]
sage: matrix(ZZ,3,[1..9]).hermite_form(algorithm='default')
[1 2 3]
[0 3 6]
[0 0 0]
The ‘ntl’ algorithm doesn’t work on matrices that do not have full rank.:
sage: matrix(ZZ,3,[1..9]).hermite_form(algorithm='ntl')
...
ValueError: ntl only computes HNF for square matrices of full rank.
sage: matrix(ZZ,3,[0] +[2..9]).hermite_form(algorithm='ntl')
[1 0 0]
[0 1 0]
[0 0 3]
Return the elementary divisors of self, in order.
Warning
This is MUCH faster than the smith_form function.
The elementary divisors are the invariants of the finite abelian group that is the cokernel of left multiplication of this matrix. They are ordered in reverse by divisibility.
INPUT:
OUTPUT: list of integers
Note
These are the invariants of the cokernel of left multiplication:
sage: M = Matrix([[3,0,1],[0,1,0]])
sage: M
[3 0 1]
[0 1 0]
sage: M.elementary_divisors()
[1, 1]
sage: M.transpose().elementary_divisors()
[1, 1, 0]
EXAMPLES:
sage: matrix(3, range(9)).elementary_divisors()
[1, 3, 0]
sage: matrix(3, range(9)).elementary_divisors(algorithm='pari')
[1, 3, 0]
sage: C = MatrixSpace(ZZ,4)([3,4,5,6,7,3,8,10,14,5,6,7,2,2,10,9])
sage: C.elementary_divisors()
[1, 1, 1, 687]
sage: M = matrix(ZZ, 3, [1,5,7, 3,6,9, 0,1,2])
sage: M.elementary_divisors()
[1, 1, 6]
This returns a copy, which is safe to change:
sage: edivs = M.elementary_divisors()
sage: edivs.pop()
6
sage: M.elementary_divisors()
[1, 1, 6]
See also
Return the Frobenius form (rational canonical form) of this matrix.
INPUT: flag -an integer:
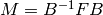 .
.INPUT:
ALGORITHM: uses pari’s matfrobenius()
EXAMPLE:
sage: A = MatrixSpace(ZZ, 3)(range(9))
sage: A.frobenius(0)
[ 0 0 0]
[ 1 0 18]
[ 0 1 12]
sage: A.frobenius(1)
[x^3 - 12*x^2 - 18*x]
sage: A.frobenius(1, var='y')
[y^3 - 12*y^2 - 18*y]
sage: A.frobenius(2)
(
[ 0 0 0] [ -1 2 -1]
[ 1 0 18] [ 0 23/15 -14/15]
[ 0 1 12], [ 0 -2/15 1/15]
)
sage: a=matrix([])
sage: a.frobenius(2)
([], [])
sage: a.frobenius(0)
[]
sage: a.frobenius(1)
[]
sage: B = random_matrix(ZZ,2,3)
sage: B.frobenius()
...
ArithmeticError: frobenius matrix of non-square matrix not defined.
AUTHORS:
TODO: - move this to work for more general matrices than just over Z. This will require fixing how PARI polynomials are coerced to Sage polynomials.
Return the gcd of all entries of self; very fast.
EXAMPLES:
sage: a = matrix(ZZ,2, [6,15,-6,150])
sage: a.gcd()
3
Return the height of this matrix, i.e., the max absolute value of the entries of the matrix.
OUTPUT: A nonnegative integer.
EXAMPLE:
sage: a = Mat(ZZ,3)(range(9))
sage: a.height()
8
sage: a = Mat(ZZ,2,3)([-17,3,-389,15,-1,0]); a
[ -17 3 -389]
[ 15 -1 0]
sage: a.height()
389
Return the Hermite normal form of self.
This is a synonym for self.echelon_form(...). See the documentation for self.echelon_form for more details.
EXAMPLES:
sage: A = matrix(ZZ, 3, 5, [-1, -1, -2, 2, -2, -4, -19, -17, 1, 2, -3, 1, 1, -4, 1])
sage: E, U = A.hermite_form(transformation=True)
sage: E
[ 1 0 52 -133 109]
[ 0 1 19 -47 38]
[ 0 0 69 -178 145]
sage: U
[-46 3 11]
[-16 1 4]
[-61 4 15]
sage: U*A
[ 1 0 52 -133 109]
[ 0 1 19 -47 38]
[ 0 0 69 -178 145]
sage: A.hermite_form()
[ 1 0 52 -133 109]
[ 0 1 19 -47 38]
[ 0 0 69 -178 145]
TESTS: This example illustrated trac 2398.
sage: a = matrix([(0, 0, 3), (0, -2, 2), (0, 1, 2), (0, -2, 5)])
sage: a.hermite_form()
[0 1 2]
[0 0 3]
[0 0 0]
[0 0 0]
Return the index of self in its saturation.
INPUT:
OUTPUT:
ALGORITHM: Use Hermite normal form twice to find an invertible matrix whose inverse transforms a matrix with the same row span as self to its saturation, then compute the determinant of that matrix.
EXAMPLES:
sage: A = matrix(ZZ, 2,3, [1..6]); A
[1 2 3]
[4 5 6]
sage: A.index_in_saturation()
3
sage: A.saturation()
[1 2 3]
[1 1 1]
Create a new matrix from self with.
INPUT:
EXAMPLES:
sage: X = matrix(ZZ,3,range(9)); X
[0 1 2]
[3 4 5]
[6 7 8]
sage: X.insert_row(1, [1,5,-10])
[ 0 1 2]
[ 1 5 -10]
[ 3 4 5]
[ 6 7 8]
sage: X.insert_row(0, [1,5,-10])
[ 1 5 -10]
[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
sage: X.insert_row(3, [1,5,-10])
[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 1 5 -10]
Return True if this lattice is
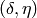 -LLL reduced. See self.LLL
for a definition of LLL reduction.
-LLL reduced. See self.LLL
for a definition of LLL reduction.
INPUT:
EXAMPLE:
sage: A = random_matrix(ZZ, 10, 10)
sage: L = A.LLL()
sage: A.is_LLL_reduced()
False
sage: L.is_LLL_reduced()
True
The options are exactly like self.kernel(...), but returns a matrix A whose rows form a basis for the left kernel, i.e., so that A*self = 0.
This is mainly useful to avoid all overhead associated with creating a free module.
INPUT:
algorithm – ‘default’, ‘pari’, or ‘padic’;
- default – choose from one of the below based
on heuristic
- 'pari' – uses pari’s matkerint function; good
for small matrices
- 'padic' – uses an asymptotically fast p-adic
algorithm; horrible for small matrices, but great for large mxn matrices with m+3 <= n.
LLL – whether to LLL reduce result (default: False)
- proof – whether result is provably correct (only
relevant for padic algorithm)
EXAMPLES:
sage: A = matrix(ZZ, 3, 3, [1..9])
sage: A.kernel_matrix()
[ 1 -2 1]
Note that the basis matrix returned above is not in Hermite/echelon form.
sage: A.kernel()
Free module of degree 3 and rank 1 over Integer Ring
Echelon basis matrix:
[ 1 -2 1]
We compute another kernel:
sage: A = matrix(ZZ, 4, 2, [2, -1, 1, 1, -18, -1, -1, -5])
sage: K = A.kernel_matrix(); K
[ -7 -3 -1 1]
[ 4 -11 0 -3]
K is a basis for the left kernel:
sage: K*A
[0 0]
[0 0]
We illustrate the LLL flag:
sage: L = A.kernel_matrix(LLL=True); L
[ -7 -3 -1 1]
[ 4 -11 0 -3]
sage: K.hermite_form()
[ 1 64 3 12]
[ 0 89 4 17]
sage: L.hermite_form()
[ 1 64 3 12]
[ 0 89 4 17]
Two kernel matrices via PARI, one of full rank:
sage: B = matrix(ZZ, [[2,-1,1],[1,-1,0],[-5,4,-1],[-8,6,-2]])
sage: B.kernel_matrix(algorithm='pari')
[ 1 1 -1 1]
[ 0 2 2 -1]
sage: C = matrix(ZZ, [[1,1,2],[1,1,4]])
sage: D = C.kernel_matrix(algorithm='pari'); D
[]
sage: D.ncols()
2
INPUT:
Note
Linbox charpoly disabled on 64-bit machines, since it hangs in many cases.
EXAMPLES:
sage: A = matrix(ZZ,6, range(36))
sage: A.minpoly()
x^3 - 105*x^2 - 630*x
sage: n=6; A = Mat(ZZ,n)([k^2 for k in range(n^2)])
sage: A.minpoly()
x^4 - 2695*x^3 - 257964*x^2 + 1693440*x
Return the pivot column positions of this matrix as a list of Python integers.
This returns a list, of the position of the first nonzero entry in each row of the echelon form.
OUTPUT:
EXAMPLES:
sage: n = 3; A = matrix(ZZ,n,range(n^2)); A
[0 1 2]
[3 4 5]
[6 7 8]
sage: A.pivots()
[0, 1]
sage: A.echelon_form()
[ 3 0 -3]
[ 0 1 2]
[ 0 0 0]
Return the product of the sums of the entries in the submatrix of self with given columns.
INPUT:
OUTPUT: an integer
EXAMPLES:
sage: a = matrix(ZZ,2,3,[1..6]); a
[1 2 3]
[4 5 6]
sage: a.prod_of_row_sums([0,2])
40
sage: (1+3)*(4+6)
40
sage: a.prod_of_row_sums(set([0,2]))
40
Randomize density proportion of the entries of this matrix, leaving the rest unchanged.
The parameters are the same as the ones for the integer ring’s random_element function.
If x and y are given, randomized entries of this matrix have to be between x and y and have density 1.
INPUT:
OUTPUT:
EXAMPLES:
sage: A = matrix(ZZ, 2,3, [1..6]); A
[1 2 3]
[4 5 6]
sage: A.randomize()
sage: A
[-8 2 0]
[ 0 1 -1]
sage: A.randomize(x=-30,y=30)
sage: A
[ 5 -19 24]
[ 24 23 -9]
Return the rank of this matrix.
OUTPUT:
Note
The rank is cached.
ALGORITHM: First check if the matrix has maxim possible rank by working modulo one random prime. If not call LinBox’s rank function.
EXAMPLES:
sage: a = matrix(ZZ,2,3,[1..6]); a
[1 2 3]
[4 5 6]
sage: a.rank()
2
sage: a = matrix(ZZ,3,3,[1..9]); a
[1 2 3]
[4 5 6]
[7 8 9]
sage: a.rank()
2
Here’s a bigger example - the rank is of course still 2:
sage: a = matrix(ZZ,100,[1..100^2]); a.rank()
2
Use rational reconstruction to lift self to a matrix over the rational numbers (if possible), where we view self as a matrix modulo N.
INPUT:
OUTPUT:
EXAMPLES: We create a random 4x4 matrix over ZZ.
sage: A = matrix(ZZ, 4, [4, -4, 7, 1, -1, 1, -1, -12, -1, -1, 1, -1, -3, 1, 5, -1])
There isn’t a unique rational reconstruction of it:
sage: A.rational_reconstruction(11)
...
ValueError: Rational reconstruction of 4 (mod 11) does not exist.
We throw in a denominator and reduce the matrix modulo 389 - it does rationally reconstruct.
sage: B = (A/3 % 389).change_ring(ZZ)
sage: B.rational_reconstruction(389) == A/3
True
Return the right kernel of a matrix over the integers.
INPUT:
OUTPUT: A module over the integers is returned. This is the saturated ZZ-module spanned by all the column vectors v such that self*v = 0.
EXAMPLES:
sage: M = MatrixSpace(ZZ,2,4)(range(8))
sage: M.right_kernel()
Free module of degree 4 and rank 2 over Integer Ring
Echelon basis matrix:
[ 1 0 -3 2]
[ 0 1 -2 1]
With zero columns the right kernel has dimension 0.
sage: M = matrix(ZZ, [[],[],[]])
sage: M.right_kernel()
Free module of degree 0 and rank 0 over Integer Ring
Echelon basis matrix:
[]
With zero rows, the whole domain is the kernel, so the dimension is the number of columns.
sage: M = matrix(ZZ, [[],[],[]]).transpose()
sage: M.right_kernel()
Ambient free module of rank 3 over the principal ideal domain Integer Ring
Return a saturation matrix of self, which is a matrix whose rows span the saturation of the row span of self. This is not unique.
The saturation of a 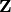 module
module 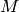 embedded in
embedded in 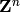 is the a module
is the a module  that
contains
that
contains 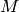 with finite index such that
with finite index such that
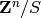 is torsion free. This function takes the
row span
is torsion free. This function takes the
row span 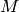 of self, and finds another matrix of full rank
with row span the saturation of
of self, and finds another matrix of full rank
with row span the saturation of 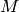 .
.
INPUT:
 , i.e., return a matrix whose row span
is a
, i.e., return a matrix whose row span
is a 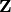 -module
-module  that contains self and
such that the index of
that contains self and
such that the index of  in its saturation is coprime to
in its saturation is coprime to
 . If
. If  is None, return full saturation of
self.
is None, return full saturation of
self.OUTPUT:
Note
The result is not cached.
ALGORITHM: 1. Replace input by a matrix of full rank got from a
subset of the rows. 2. Divide out any common factors from rows. 3.
Check max_dets random dets of submatrices to see if their GCD
(with p) is 1 - if so matrix is saturated and we’re done. 4.
Finally, use that if A is a matrix of full rank, then
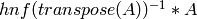 is a saturation of A.
is a saturation of A.
EXAMPLES:
sage: A = matrix(ZZ, 3, 5, [-51, -1509, -71, -109, -593, -19, -341, 4, 86, 98, 0, -246, -11, 65, 217])
sage: A.echelon_form()
[ 1 5 2262 20364 56576]
[ 0 6 35653 320873 891313]
[ 0 0 42993 386937 1074825]
sage: S = A.saturation(); S
[ -51 -1509 -71 -109 -593]
[ -19 -341 4 86 98]
[ 35 994 43 51 347]
Notice that the saturation spans a different module than A.
sage: S.echelon_form()
[ 1 2 0 8 32]
[ 0 3 0 -2 -6]
[ 0 0 1 9 25]
sage: V = A.row_space(); W = S.row_space()
sage: V.is_submodule(W)
True
sage: V.index_in(W)
85986
sage: V.index_in_saturation()
85986
We illustrate each option:
sage: S = A.saturation(p=2)
sage: S = A.saturation(proof=False)
sage: S = A.saturation(max_dets=2)
Returns matrices S, U, and V such that S = U*self*V, and S is in Smith normal form. Thus S is diagonal with diagonal entries the ordered elementary divisors of S.
Warning
The elementary_divisors function, which returns the diagonal entries of S, is VASTLY faster than this function.
The elementary divisors are the invariants of the finite abelian group that is the cokernel of this matrix. They are ordered in reverse by divisibility.
EXAMPLES:
sage: A = MatrixSpace(IntegerRing(), 3)(range(9))
sage: D, U, V = A.smith_form()
sage: D
[1 0 0]
[0 3 0]
[0 0 0]
sage: U
[ 0 1 0]
[ 0 -1 1]
[-1 2 -1]
sage: V
[-1 4 1]
[ 1 -3 -2]
[ 0 0 1]
sage: U*A*V
[1 0 0]
[0 3 0]
[0 0 0]
It also makes sense for nonsquare matrices:
sage: A = Matrix(ZZ,3,2,range(6))
sage: D, U, V = A.smith_form()
sage: D
[1 0]
[0 2]
[0 0]
sage: U
[ 0 1 0]
[ 0 -1 1]
[-1 2 -1]
sage: V
[-1 3]
[ 1 -2]
sage: U * A * V
[1 0]
[0 2]
[0 0]
Empty matrices are handled sensibly (see trac #3068):
sage: m = MatrixSpace(ZZ, 2,0)(0); d,u,v = m.smith_form(); u*m*v == d
True
sage: m = MatrixSpace(ZZ, 0,2)(0); d,u,v = m.smith_form(); u*m*v == d
True
sage: m = MatrixSpace(ZZ, 0,0)(0); d,u,v = m.smith_form(); u*m*v == d
True
See also
Return the matrix self on top of other: [ self ] [ other ]
EXAMPLES:
sage: M = Matrix(ZZ, 2, 3, range(6))
sage: N = Matrix(ZZ, 1, 3, [10,11,12])
sage: M.stack(N)
[ 0 1 2]
[ 3 4 5]
[10 11 12]
Find a symplectic basis for self if self is an anti-symmetric, alternating matrix.
Returns a pair (F, C) such that the rows of C form a symplectic basis for self and F = C * self * C.transpose().
Raises a ValueError if self is not anti-symmetric, or self is not alternating.
Anti-symmetric means that 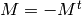 . Alternating means
that the diagonal of
. Alternating means
that the diagonal of 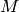 is identically zero.
is identically zero.
A symplectic basis is a basis of the form
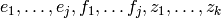 such that
such that
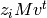 = 0 for all vectors
= 0 for all vectors 
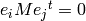 for all
for all 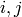
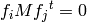 for all
for all 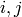
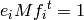 for all
for all 
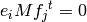 for all
for all  not equal
not equal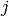 .
.
The ordering for the factors 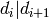 and for
the placement of zeroes was chosen to agree with the output of
smith_form.
and for
the placement of zeroes was chosen to agree with the output of
smith_form.
See the example for a pictorial description of such a basis.
EXAMPLES:
sage: E = matrix(ZZ, 5, 5, [0, 14, 0, -8, -2, -14, 0, -3, -11, 4, 0, 3, 0, 0, 0, 8, 11, 0, 0, 8, 2, -4, 0, -8, 0]); E
[ 0 14 0 -8 -2]
[-14 0 -3 -11 4]
[ 0 3 0 0 0]
[ 8 11 0 0 8]
[ 2 -4 0 -8 0]
sage: F, C = E.symplectic_form()
sage: F
[ 0 0 1 0 0]
[ 0 0 0 2 0]
[-1 0 0 0 0]
[ 0 -2 0 0 0]
[ 0 0 0 0 0]
sage: F == C * E * C.transpose()
True
sage: E.smith_form()[0]
[1 0 0 0 0]
[0 1 0 0 0]
[0 0 2 0 0]
[0 0 0 2 0]
[0 0 0 0 0]
Returns the transpose of self, without changing self.
EXAMPLES:
We create a matrix, compute its transpose, and note that the original matrix is not changed.
sage: A = matrix(ZZ,2,3,xrange(6))
sage: type(A)
<type 'sage.matrix.matrix_integer_dense.Matrix_integer_dense'>
sage: B = A.transpose()
sage: print B
[0 3]
[1 4]
[2 5]
sage: print A
[0 1 2]
[3 4 5]
sage: A.subdivide(None, 1); A
[0|1 2]
[3|4 5]
sage: A.transpose()
[0 3]
[---]
[1 4]
[2 5]
Compare various multiplication algorithms.
INPUT:
OUTPUT:
EXAMPLES:
sage: from sage.matrix.matrix_integer_dense import tune_multiplication
sage: tune_multiplication(2, nmin=10, nmax=60, bitmin=2,bitmax=8)
10 2 0.2
...