Permutation group elements¶

AUTHORS:

David Joyner (2006-02)
David Joyner (2006-03): word problem method and reorganization
Robert Bradshaw (2007-11): convert to Cython

EXAMPLES: The Rubik’s cube group:

sage: f= [(17,19,24,22),(18,21,23,20),(6,25,43,16),(7,28,42,13),(8,30,41,11)]
sage: b=[(33,35,40,38),(34,37,39,36),( 3, 9,46,32),( 2,12,47,29),( 1,14,48,27)]
sage: l=[( 9,11,16,14),(10,13,15,12),( 1,17,41,40),( 4,20,44,37),( 6,22,46,35)]
sage: r=[(25,27,32,30),(26,29,31,28),( 3,38,43,19),( 5,36,45,21),( 8,33,48,24)]
sage: u=[( 1, 3, 8, 6),( 2, 5, 7, 4),( 9,33,25,17),(10,34,26,18),(11,35,27,19)]
sage: d=[(41,43,48,46),(42,45,47,44),(14,22,30,38),(15,23,31,39),(16,24,32,40)]
sage: cube = PermutationGroup([f,b,l,r,u,d])
sage: F=cube.gens()[0]
sage: B=cube.gens()[1]
sage: L=cube.gens()[2]
sage: R=cube.gens()[3]
sage: U=cube.gens()[4]
sage: D=cube.gens()[5]
sage: cube.order()
43252003274489856000
sage: F.order()
4

The interested user may wish to explore the following commands: move = cube.random_element() and time word_problem([F,B,L,R,U,D], move, False). This typically takes about 5 minutes (on a 2 Ghz machine) and outputs a word (‘solving’ the cube in the position move) with about 60 terms or so.

OTHER EXAMPLES: We create element of a permutation group of large degree.

sage: G = SymmetricGroup(30)
sage: s = G(srange(30,0,-1)); s
(1,30)(2,29)(3,28)(4,27)(5,26)(6,25)(7,24)(8,23)(9,22)(10,21)(11,20)(12,19)(13,18)(14,17)(15,16)

class sage.groups.perm_gps.permgroup_element.PermutationGroupElement¶

Bases: sage.structure.element.MultiplicativeGroupElement

An element of a permutation group.

EXAMPLES:

sage: G = PermutationGroup(['(1,2,3)(4,5)'])
sage: G
Permutation Group with generators [(1,2,3)(4,5)]
sage: g = G.random_element()
sage: g in G
True
sage: g = G.gen(0); g
(1,2,3)(4,5)
sage: print g
(1,2,3)(4,5)
sage: g*g
(1,3,2)
sage: g**(-1)
(1,3,2)(4,5)
sage: g**2
(1,3,2)
sage: G = PermutationGroup([(1,2,3)])
sage: g = G.gen(0); g
(1,2,3)
sage: g.order()
3

This example illustrates how permutations act on multivariate polynomials.

sage: R = PolynomialRing(RationalField(), 5, ["x","y","z","u","v"])
sage: x, y, z, u, v = R.gens()
sage: f = x**2 - y**2 + 3*z**2
sage: G = PermutationGroup(['(1,2,3)(4,5)', '(1,2,3,4,5)'])
sage: sigma = G.gen(0)
sage: f * sigma
3*x^2 + y^2 - z^2

cycle_tuples()¶: Return self as a list of disjoint cycles, represented as tuples rather than permutation group elements.

cycles()¶

Return self as a list of disjoint cycles.

EXAMPLES:

sage: G = PermutationGroup(['(1,2,3)(4,5,6,7)'])
sage: g = G.0
sage: g.cycles()
[(1,2,3), (4,5,6,7)]
sage: a, b = g.cycles()
sage: a(1), b(1)
(2, 1)

dict()¶

Returns list of the images of the integers from 1 to n under this permutation as a list of Python ints.

Note

list() returns a zero-indexed list. dict() return the actual mapping of the permutation, which will be indexed starting with 1.

EXAMPLES:

sage: G = SymmetricGroup(4)
sage: g = G((1,2,3,4)); g
(1,2,3,4)
sage: v = g.dict(); v
{1: 2, 2: 3, 3: 4, 4: 1}
sage: type(v[1])
<type 'int'>
sage: x = G([2,1]); x
(1,2)
sage: x.dict()
{1: 2, 2: 1, 3: 3, 4: 4}

has_descent(i, side='right', positive=False)¶

INPUT:

i: an element of the index set

side: “left” or “right” (default: “right”)

positive: a boolean (default: False)

Returns whether self has a left (resp. right) descent at position i. If positive is True, then test for a non descent instead.

Beware that, since permutations are acting on the right, the meaning of descents is the reverse of the usual convention. Hence, self has a left descent at position i if self(i) > self(i+1).

EXAMPLES:

sage: S = SymmetricGroup([1,2,3])
sage: S.one().has_descent(1)
False
sage: S.one().has_descent(2)
False
sage: s = S.simple_reflections()
sage: x = s[1]*s[2]
sage: x.has_descent(1, side = "right")
False
sage: x.has_descent(2, side = "right")
True
sage: x.has_descent(1, side = "left")
True
sage: x.has_descent(2, side = "left")
False
sage: S._test_has_descent()

The symmetric group acting on a set not of the form 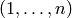$(1,\dots,n)$ is also supported:

sage: S = SymmetricGroup([2,4,1])
sage: s = S.simple_reflections()
sage: x = s[2]*s[4]
sage: x.has_descent(4)
True
sage: S._test_has_descent()

list()¶

Returns list of the images of the integers from 1 to n under this permutation as a list of Python ints.

EXAMPLES:

sage: G = SymmetricGroup(4)
sage: x = G([2,1,4,3]); x
(1,2)(3,4)
sage: v = x.list(); v
[2, 1, 4, 3]
sage: type(v[0])
<type 'int'>
sage: x = G([2,1]); x
(1,2)
sage: x.list()
[2, 1, 3, 4]

matrix()¶

Returns deg x deg permutation matrix associated to the permutation self

EXAMPLES:

sage: G = PermutationGroup(['(1,2,3)(4,5)'])
sage: g = G.gen(0)
sage: g.matrix()
[0 1 0 0 0]
[0 0 1 0 0]
[1 0 0 0 0]
[0 0 0 0 1]
[0 0 0 1 0]

orbit(n, sorted=True)¶

Returns the orbit of the integer $n$ under this group element, as a sorted list of integers.

EXAMPLES:

sage: G = PermutationGroup(['(1,2,3)(4,5)'])
sage: g = G.gen(0)
sage: g.orbit(4)
[4, 5]
sage: g.orbit(3)
[1, 2, 3]
sage: g.orbit(10)
[10]

order()¶

Return the order of this group element, which is the smallest positive integer $n$ for which $g^n = 1$ .

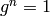EXAMPLES:

sage: s = PermutationGroupElement('(1,2)(3,5,6)')
sage: s.order()
6

TESTS:

sage: prod(primes(150))
1492182350939279320058875736615841068547583863326864530410
sage: L = [tuple(range(sum(primes(p))+1, sum(primes(p))+1+p)) for p in primes(150)]
sage: PermutationGroupElement(L).order()
1492182350939279320058875736615841068547583863326864530410

sign()¶

Returns the sign of self, which is 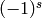$(-1)^{s}$ , where $s$ is the number of swaps.

EXAMPLES:

sage: s = PermutationGroupElement('(1,2)(3,5,6)')
sage: s.sign()
-1

ALGORITHM: Only even cycles contribute to the sign, thus

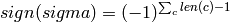
$sign(sigma) = (-1)^{\sum_c len(c)-1}$

where the sum is over cycles in self.

tuple()¶

Return tuple of images of integers under self.

EXAMPLES:

sage: G = SymmetricGroup(5)
sage: s = G([2,1,5,3,4])
sage: s.tuple()
(2, 1, 5, 3, 4)

word_problem(g, words, display=True)¶

G and H are permutation groups, g in G, H is a subgroup of G generated by a list (words) of elements of G. If g is in H, return the expression for g as a word in the elements of (words).

This function does not solve the word problem in Sage. Rather it pushes it over to GAP, which has optimized algorithms for the word problem. Essentially, this function is a wrapper for the GAP functions “EpimorphismFromFreeGroup” and “PreImagesRepresentative”.

EXAMPLE:

sage: G = PermutationGroup([[(1,2,3),(4,5)],[(3,4)]], canonicalize=False)
sage: g1 = G.gens()[0]
sage: g2 = G.gens()[1]
sage: h = g1^2*g2*g1
sage: h.word_problem([g1,g2], False)
('x1^2*x2^-1*x1', '(1,2,3)(4,5)^2*(3,4)^-1*(1,2,3)(4,5)')
sage: h.word_problem([g1,g2])
   x1^2*x2^-1*x1
   [['(1,2,3)(4,5)', 2], ['(3,4)', -1], ['(1,2,3)(4,5)', 1]]
('x1^2*x2^-1*x1', '(1,2,3)(4,5)^2*(3,4)^-1*(1,2,3)(4,5)')

sage.groups.perm_gps.permgroup_element.gap_format(x)¶: Put a permutation in Gap format, as a string.

sage.groups.perm_gps.permgroup_element.is_PermutationGroupElement(x)¶

sage.groups.perm_gps.permgroup_element.make_permgroup_element(G, x)¶

sage.groups.perm_gps.permgroup_element.string_to_tuples(g)¶

EXAMPLES:

sage: from sage.groups.perm_gps.permgroup_element import string_to_tuples
sage: string_to_tuples('(1,2,3)')
[(1, 2, 3)]
sage: string_to_tuples('(1,2,3)(4,5)')
[(1, 2, 3), (4, 5)]
sage: string_to_tuples(' (1,2, 3) (4,5)')
[(1, 2, 3), (4, 5)]
sage: string_to_tuples('(1,2)(3)')
[(1, 2), (3,)]

Permutation group elements¶

Previous topic

Next topic

This Page

Navigation

Permutation group elements¶

Previous topic

Next topic

This Page

Quick search

Navigation