A permutation group is a finite group  whose elements are
permutations of a given finite set
whose elements are
permutations of a given finite set  (i.e., bijections
(i.e., bijections
 ) and whose group operation is the composition of
permutations. The number of elements of
) and whose group operation is the composition of
permutations. The number of elements of  is called the degree of
is called the degree of  .
.
In Sage, a permutation is represented as either a string that defines a permutation using disjoint cycle notation, or a list of tuples, which represent disjoint cycles. That is:
(a,...,b)(c,...,d)...(e,...,f) <--> [(a,...,b), (c,...,d),..., (e,...,f)]
() = identity <--> []
You can make the “named” permutation groups (see permgp_named.py) and use the following constructions:
JOKE: Q: What’s hot, chunky, and acts on a polygon? A: Dihedral soup. Renteln, P. and Dundes, A. “Foolproof: A Sampling of Mathematical Folk Humor.” Notices Amer. Math. Soc. 52, 24-34, 2005.
AUTHORS:
REFERENCES:
Note
Though Suzuki groups are okay, Ree groups should not be wrapped as permutation groups - the construction is too slow - unless (for small values or the parameter) they are made using explicit generators.
Return the permutation group associated to  (typically a
list of generators).
(typically a
list of generators).
INPUT:
OUTPUT:
EXAMPLES:
sage: G = PermutationGroup([[(1,2,3),(4,5)],[(3,4)]])
sage: G
Permutation Group with generators [(3,4), (1,2,3)(4,5)]
We can also make permutation groups from PARI groups:
sage: H = pari('x^4 - 2*x^3 - 2*x + 1').polgalois()
sage: G = PariGroup(H, 4); G
PARI group [8, -1, 3, "D(4)"] of degree 4
sage: H = PermutationGroup(G); H # optional - database_gap
Transitive group number 3 of degree 4
sage: H.gens() # optional - database_gap
[(1,2,3,4), (1,3)]
We can also create permutation groups whose generators are Gap permutation objects:
sage: p = gap('(1,2)(3,7)(4,6)(5,8)'); p
(1,2)(3,7)(4,6)(5,8)
sage: PermutationGroup([p])
Permutation Group with generators [(1,2)(3,7)(4,6)(5,8)]
There is an underlying gap object that implements each permutation group:
sage: G = PermutationGroup([[(1,2,3,4)]])
sage: G._gap_()
Group( [ (1,2,3,4) ] )
sage: gap(G)
Group( [ (1,2,3,4) ] )
sage: gap(G) is G._gap_()
True
sage: G = PermutationGroup([[(1,2,3),(4,5)],[(3,4)]])
sage: current_randstate().set_seed_gap()
sage: G._gap_().DerivedSeries()
[ Group( [ (3,4), (1,2,3)(4,5) ] ), Group( [ (1,5)(3,4), (1,5)(2,4), (1,5,3) ] ) ]
TESTS:
sage: PermutationGroup(SymmetricGroup(5))
...
TypeError: gens must be a tuple, list, or GapElement
Bases: sage.groups.group.Group
EXAMPLES:
sage: G = PermutationGroup([[(1,2,3),(4,5)],[(3,4)]])
sage: G
Permutation Group with generators [(3,4), (1,2,3)(4,5)]
sage: G.center()
Permutation Group with generators [()]
sage: G.group_id() # optional - database_gap
[120, 34]
sage: n = G.order(); n
120
sage: G = PermutationGroup([[(1,2,3),(4,5)],[(3,4)]])
sage: TestSuite(G).run()
Return the subgroup of elements that commute with every element of this group.
EXAMPLES:
sage: G = PermutationGroup([[(1,2,3,4)]])
sage: G.center()
Permutation Group with generators [(1,2,3,4)]
sage: G = PermutationGroup([[(1,2,3,4)], [(1,2)]])
sage: G.center()
Permutation Group with generators [()]
Returns the centralizer of g in self.
EXAMPLES:
sage: G = PermutationGroup([[(1,2),(3,4)], [(1,2,3,4)]])
sage: g = G([(1,3)])
sage: G.centralizer(g)
Permutation Group with generators [(2,4), (1,3)]
sage: g = G([(1,2,3,4)])
sage: G.centralizer(g)
Permutation Group with generators [(1,2,3,4)]
sage: H = G.subgroup([G([(1,2,3,4)])])
sage: G.centralizer(H)
Permutation Group with generators [(1,2,3,4)]
Returns a group character from values, where values is a list of the values of the character evaluated on the conjugacy classes.
EXAMPLES:
sage: G = AlternatingGroup(4)
sage: n = len(G.conjugacy_classes_representatives())
sage: G.character([1]*n)
Character of Alternating group of order 4!/2 as a permutation group
Returns the matrix of values of the irreducible characters of a
permutation group  at the conjugacy classes of
at the conjugacy classes of
 . The columns represent the conjugacy classes of
. The columns represent the conjugacy classes of
 and the rows represent the different irreducible
characters in the ordering given by GAP.
and the rows represent the different irreducible
characters in the ordering given by GAP.
EXAMPLES:
sage: G = PermutationGroup([[(1,2),(3,4)], [(1,2,3)]])
sage: G.order()
12
sage: G.character_table()
[ 1 1 1 1]
[ 1 1 -zeta3 - 1 zeta3]
[ 1 1 zeta3 -zeta3 - 1]
[ 3 -1 0 0]
sage: G = PermutationGroup([[(1,2),(3,4)], [(1,2,3)]])
sage: CT = gap(G).CharacterTable()
Type print gap.eval("Display(%s)"%CT.name()) to display this nicely.
sage: G = PermutationGroup([[(1,2),(3,4)], [(1,2,3,4)]])
sage: G.order()
8
sage: G.character_table()
[ 1 1 1 1 1]
[ 1 -1 -1 1 1]
[ 1 -1 1 -1 1]
[ 1 1 -1 -1 1]
[ 2 0 0 0 -2]
sage: CT = gap(G).CharacterTable()
Again, type print gap.eval("Display(%s)"%CT.name()) to display this nicely.
sage: SymmetricGroup(2).character_table()
[ 1 -1]
[ 1 1]
sage: SymmetricGroup(3).character_table()
[ 1 -1 1]
[ 2 0 -1]
[ 1 1 1]
sage: SymmetricGroup(5).character_table()
[ 1 -1 1 1 -1 -1 1]
[ 4 -2 0 1 1 0 -1]
[ 5 -1 1 -1 -1 1 0]
[ 6 0 -2 0 0 0 1]
[ 5 1 1 -1 1 -1 0]
[ 4 2 0 1 -1 0 -1]
[ 1 1 1 1 1 1 1]
sage: list(AlternatingGroup(6).character_table())
[(1, 1, 1, 1, 1, 1, 1), (5, 1, 2, -1, -1, 0, 0), (5, 1, -1, 2, -1, 0, 0), (8, 0, -1, -1, 0, zeta5^3 + zeta5^2 + 1, -zeta5^3 - zeta5^2), (8, 0, -1, -1, 0, -zeta5^3 - zeta5^2, zeta5^3 + zeta5^2 + 1), (9, 1, 0, 0, 1, -1, -1), (10, -2, 1, 1, 0, 0, 0)]
Suppose that you have a class function 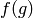 on
on
 and you know the values
and you know the values 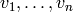 on
the conjugacy class elements in
conjugacy_classes_representatives(G) =
on
the conjugacy class elements in
conjugacy_classes_representatives(G) =
![[g_1, \ldots, g_n]](../../../_images/math/1f37c19ce8b8b296a5732765989850f3163bce2a.png) . Since the irreducible characters
. Since the irreducible characters
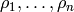 of
of  form an
form an
 -basis of the space of all class functions (
-basis of the space of all class functions ( a “sufficiently large” cyclotomic field), such a class function is
a linear combination of these basis elements,
a “sufficiently large” cyclotomic field), such a class function is
a linear combination of these basis elements,
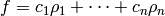 . To find
the coefficients
. To find
the coefficients 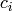 , you simply solve the linear system
character_table_values(G)
, you simply solve the linear system
character_table_values(G) ![[v_1, ..., v_n] = [c_1, ..., c_n]](../../../_images/math/9132489bc13a168cb834eff944994eedf1811858.png) ,
where
,
where ![[v_1, \ldots, v_n]](../../../_images/math/b78ff7ca5659f1cc1394aad2ae0790cad56ccbe8.png) = character_table_values(G)
= character_table_values(G) ![^{(-1)}[c_1, ..., c_n]](../../../_images/math/3f145014c1ba2aa1695a3bcfeaf2a6cfb45e0047.png) .
.
AUTHORS:
Computes the group cohomology 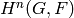 , where
, where 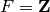 if
if 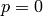 and
and 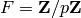 if
if 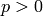 is a prime.
Wraps HAP’s GroupHomology function, written by Graham Ellis.
is a prime.
Wraps HAP’s GroupHomology function, written by Graham Ellis.
REQUIRES: GAP package HAP (in gap_packages-*.spkg).
EXAMPLES:
sage: G = SymmetricGroup(4)
sage: G.cohomology(1,2) # optional - gap_packages
Multiplicative Abelian Group isomorphic to C2
sage: G = SymmetricGroup(3)
sage: G.cohomology(5) # optional - gap_packages
Trivial Abelian Group
sage: G.cohomology(5,2) # optional - gap_packages
Multiplicative Abelian Group isomorphic to C2
sage: G.homology(5,3) # optional - gap_packages
Trivial Abelian Group
sage: G.homology(5,4) # optional - gap_packages
...
ValueError: p must be 0 or prime
This computes 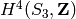 and
and
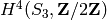 , respectively.
, respectively.
AUTHORS:
REFERENCES:
Computes the p-part of the group cohomology 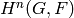 ,
where
,
where 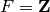 if
if 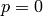 and
and 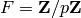 if
if
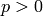 is a prime. Wraps HAP’s Homology function, written
by Graham Ellis, applied to the
is a prime. Wraps HAP’s Homology function, written
by Graham Ellis, applied to the  -Sylow subgroup of
-Sylow subgroup of
 .
.
REQUIRES: GAP package HAP (in gap_packages-*.spkg).
EXAMPLES:
sage: G = SymmetricGroup(5)
sage: G.cohomology_part(7,2) # optional - gap_packages
Multiplicative Abelian Group isomorphic to C2 x C2 x C2
sage: G = SymmetricGroup(3)
sage: G.cohomology_part(2,3) # optional - gap_packages
Multiplicative Abelian Group isomorphic to C3
AUTHORS:
Return the composition series of this group as a list of permutation groups.
EXAMPLES:
These computations use pseudo-random numbers, so we set the seed for reproducible testing.
sage: set_random_seed(0)
sage: G = PermutationGroup([[(1,2,3),(4,5)],[(3,4)]])
sage: G.composition_series() # random output
[Permutation Group with generators [(1,2,3)(4,5), (3,4)], Permutation Group with generators [(1,5)(3,4), (1,5)(2,3), (1,5,4)], Permutation Group with generators [()]]
sage: G = PermutationGroup([[(1,2,3),(4,5)], [(1,2)]])
sage: CS = G.composition_series()
sage: CS[3]
Permutation Group with generators [()]
Returns a complete list of representatives of conjugacy classes in
a permutation group  . The ordering is that given by GAP.
. The ordering is that given by GAP.
EXAMPLES:
sage: G = PermutationGroup([[(1,2),(3,4)], [(1,2,3,4)]])
sage: cl = G.conjugacy_classes_representatives(); cl
[(), (2,4), (1,2)(3,4), (1,2,3,4), (1,3)(2,4)]
sage: cl[3] in G
True
sage: G = SymmetricGroup(5)
sage: G.conjugacy_classes_representatives ()
[(), (1,2), (1,2)(3,4), (1,2,3), (1,2,3)(4,5), (1,2,3,4), (1,2,3,4,5)]
AUTHORS:
Returns a complete list of representatives of conjugacy classes of
subgroups in a permutation group  . The ordering is that given by
GAP.
. The ordering is that given by
GAP.
EXAMPLES:
sage: G = PermutationGroup([[(1,2),(3,4)], [(1,2,3,4)]])
sage: cl = G.conjugacy_classes_subgroups()
sage: cl
[Permutation Group with generators [()],
Permutation Group with generators [(1,2)(3,4)],
Permutation Group with generators [(1,3)(2,4)],
Permutation Group with generators [(2,4)],
Permutation Group with generators [(1,4)(2,3), (1,2)(3,4)],
Permutation Group with generators [(1,3)(2,4), (2,4)],
Permutation Group with generators [(1,3)(2,4), (1,2,3,4)],
Permutation Group with generators [(1,3)(2,4), (1,2)(3,4), (1,2,3,4)]]
sage: G = SymmetricGroup(3)
sage: G.conjugacy_classes_subgroups()
[Permutation Group with generators [()],
Permutation Group with generators [(2,3)],
Permutation Group with generators [(1,2,3)],
Permutation Group with generators [(1,3,2), (1,2)]]
AUTHORS:
EXAMPLES:
sage: P1 = PermutationGroup([[(1,2)]])
sage: P1.construction()
(PermutationGroupFunctor[(1,2)], Permutation Group with generators [()])
sage: PermutationGroup([]).construction() is None
True
This allows us to perform computations like the following:
sage: P1 = PermutationGroup([[(1,2)]]); p1 = P1.gen()
sage: P2 = PermutationGroup([[(1,3)]]); p2 = P2.gen()
sage: p = p1*p2; p
(1,2,3)
sage: p.parent()
Permutation Group with generators [(1,2), (1,3)]
Return the largest point moved by a permutation in this group.
EXAMPLES:
sage: G = PermutationGroup([[(1,2),(3,4)], [(1,2,3,4)]])
sage: G.largest_moved_point()
4
sage: G = PermutationGroup([[(1,2),(3,4)], [(1,2,3,4,10)]])
sage: G.largest_moved_point()
10
sage: G = PermutationGroup([[(1,2,3),(4,5)],[(3,4)]])
sage: G.degree()
5
TODO: the name of this function is not good; this function should be deprecated in term of degree:
sage: P = PermutationGroup([[1,2,3,4]])
sage: P.largest_moved_point()
4
sage: P.cardinality()
1
Return the derived series of this group as a list of permutation groups.
EXAMPLES:
These computations use pseudo-random numbers, so we set the seed for reproducible testing.
sage: set_random_seed(0)
sage: G = PermutationGroup([[(1,2,3),(4,5)],[(3,4)]])
sage: G.derived_series() # random output
[Permutation Group with generators [(1,2,3)(4,5), (3,4)], Permutation Group with generators [(1,5)(3,4), (1,5)(2,4), (2,4)(3,5)]]
Wraps GAP’s DirectProduct, Embedding, and Projection.
Sage calls GAP’s DirectProduct, which chooses an efficient representation for the direct product. The direct product of permutation groups will be a permutation group again. For a direct product D, the GAP operation Embedding(D,i) returns the homomorphism embedding the i-th factor into D. The GAP operation Projection(D,i) gives the projection of D onto the i-th factor. This method returns a 5-tuple: a permutation group and 4 morphisms.
INPUT:
OUTPUT:
EXAMPLES:
sage: G = CyclicPermutationGroup(4)
sage: D = G.direct_product(G,False)
sage: D
Permutation Group with generators [(1,2,3,4), (5,6,7,8)]
sage: D,iota1,iota2,pr1,pr2 = G.direct_product(G)
sage: D; iota1; iota2; pr1; pr2
Permutation Group with generators [(1,2,3,4), (5,6,7,8)]
Homomorphism : Cyclic group of order 4 as a permutation group --> Permutation Group with generators [(1,2,3,4), (5,6,7,8)]
Homomorphism : Cyclic group of order 4 as a permutation group --> Permutation Group with generators [(1,2,3,4), (5,6,7,8)]
Homomorphism : Permutation Group with generators [(1,2,3,4), (5,6,7,8)] --> Cyclic group of order 4 as a permutation group
Homomorphism : Permutation Group with generators [(1,2,3,4), (5,6,7,8)] --> Cyclic group of order 4 as a permutation group
sage: g=D([(1,3),(2,4)]); g
(1,3)(2,4)
sage: d=D([(1,4,3,2),(5,7),(6,8)]); d
(1,4,3,2)(5,7)(6,8)
sage: iota1(g); iota2(g); pr1(d); pr2(d)
(1,3)(2,4)
(5,7)(6,8)
(1,4,3,2)
(1,3)(2,4)
Computes the exponent of the group. The exponent  of a
group
of a
group  is the LCM of the orders of its elements, that
is,
is the LCM of the orders of its elements, that
is,  is the smallest integer such that
is the smallest integer such that 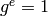 for all
for all 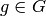 .
.
EXAMPLES:
sage: G = AlternatingGroup(4)
sage: G.exponent()
6
Returns the i-th generator of self; that is, the i-th element of the list self.gens().
The argument  may be omitted if there is only one generator (but
this will raise an error otherwise).
may be omitted if there is only one generator (but
this will raise an error otherwise).
EXAMPLES:
We explicitly construct the alternating group on four elements:
sage: A4 = PermutationGroup([[(1,2,3)],[(2,3,4)]]); A4
Permutation Group with generators [(2,3,4), (1,2,3)]
sage: A4.gens()
[(2,3,4), (1,2,3)]
sage: A4.gen(0)
(2,3,4)
sage: A4.gen(1)
(1,2,3)
sage: A4.gens()[0]; A4.gens()[1]
(2,3,4)
(1,2,3)
sage: P1 = PermutationGroup([[(1,2)]]); P1.gen()
(1,2)
Return tuple of generators of this group. These need not be minimal, as they are the generators used in defining this group.
EXAMPLES:
sage: G = PermutationGroup([[(1,2,3)], [(1,2)]])
sage: G.gens()
[(1,2), (1,2,3)]
Note that the generators need not be minimal, though duplicates are removed:
sage: G = PermutationGroup([[(1,2)], [(1,3)], [(2,3)], [(1,2)]])
sage: G.gens()
[(2,3), (1,2), (1,3)]
We can use index notation to access the generators returned by self.gens:
sage: G = PermutationGroup([[(1,2,3,4), (5,6)], [(1,2)]])
sage: g = G.gens()
sage: g[0]
(1,2)
sage: g[1]
(1,2,3,4)(5,6)
TESTS:
We make sure that the trivial group gets handled correctly:
sage: SymmetricGroup(1).gens()
[()]
For this group, returns a generating set which has few elements. As neither irredundancy nor minimal length is proven, it is fast.
EXAMPLES:
sage: R = "(25,27,32,30)(26,29,31,28)( 3,38,43,19)( 5,36,45,21)( 8,33,48,24)" ## R = right
sage: U = "( 1, 3, 8, 6)( 2, 5, 7, 4)( 9,33,25,17)(10,34,26,18)(11,35,27,19)" ## U = top
sage: L = "( 9,11,16,14)(10,13,15,12)( 1,17,41,40)( 4,20,44,37)( 6,22,46,35)" ## L = left
sage: F = "(17,19,24,22)(18,21,23,20)( 6,25,43,16)( 7,28,42,13)( 8,30,41,11)" ## F = front
sage: B = "(33,35,40,38)(34,37,39,36)( 3, 9,46,32)( 2,12,47,29)( 1,14,48,27)" ## B = back or rear
sage: D = "(41,43,48,46)(42,45,47,44)(14,22,30,38)(15,23,31,39)(16,24,32,40)" ## D = down or bottom
sage: G = PermutationGroup([R,L,U,F,B,D])
sage: len(G.gens_small())
2
Return the ID code of this group, which is a list of two integers. Requires “optional” database_gap-4.4.x package.
EXAMPLES:
sage: G = PermutationGroup([[(1,2,3),(4,5)], [(1,2)]])
sage: G.group_id() # optional - database_gap
[12, 4]
Returns boolean value of item in self - however ignores parentage.
EXAMPLES:
sage: G = CyclicPermutationGroup(4)
sage: gens = G.gens()
sage: H = DihedralGroup(4)
sage: g = G([(1,2,3,4)]); g
(1,2,3,4)
sage: G.has_element(g)
True
sage: h = H([(1,2),(3,4)]); h
(1,2)(3,4)
sage: G.has_element(h)
False
Computes the group homology 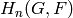 , where
, where
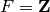 if
if 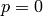 and
and 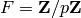 if
if
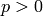 is a prime. Wraps HAP’s GroupHomology function,
written by Graham Ellis.
is a prime. Wraps HAP’s GroupHomology function,
written by Graham Ellis.
REQUIRES: GAP package HAP (in gap_packages-*.spkg).
AUTHORS:
The example below computes 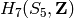 ,
,
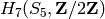 ,
,
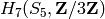 , and
, and
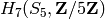 , respectively. To compute the
, respectively. To compute the
 -part of
-part of 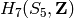 , use the homology_part
function.
, use the homology_part
function.
EXAMPLES:
sage: G = SymmetricGroup(5)
sage: G.homology(7) # optional - gap_packages
Multiplicative Abelian Group isomorphic to C2 x C2 x C4 x C3 x C5
sage: G.homology(7,2) # optional - gap_packages
Multiplicative Abelian Group isomorphic to C2 x C2 x C2 x C2 x C2
sage: G.homology(7,3) # optional - gap_packages
Multiplicative Abelian Group isomorphic to C3
sage: G.homology(7,5) # optional - gap_packages
Multiplicative Abelian Group isomorphic to C5
REFERENCES:
Computes the  -part of the group homology
-part of the group homology
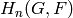 , where
, where 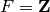 if
if 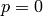 and
and
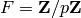 if
if 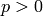 is a prime. Wraps HAP’s
Homology function, written by Graham Ellis, applied to the
is a prime. Wraps HAP’s
Homology function, written by Graham Ellis, applied to the
 -Sylow subgroup of
-Sylow subgroup of  .
.
REQUIRES: GAP package HAP (in gap_packages-*.spkg).
EXAMPLES:
sage: G = SymmetricGroup(5)
sage: G.homology_part(7,2) # optional - gap_packages
Multiplicative Abelian Group isomorphic to C2 x C2 x C2 x C2 x C4
AUTHORS:
(Same as self.group_id().) Return the ID code of this group, which is a list of two integers. Requires “optional” database_gap-4.4.x package.
EXAMPLES:
sage: G = PermutationGroup([[(1,2,3),(4,5)], [(1,2)]])
sage: G.group_id() # optional - database_gap
[12, 4]
Return the identity element of this group.
EXAMPLES:
sage: G = PermutationGroup([[(1,2,3),(4,5)]])
sage: e = G.identity()
sage: e
()
sage: g = G.gen(0)
sage: g*e
(1,2,3)(4,5)
sage: e*g
(1,2,3)(4,5)
Returns a list of the irreducible characters of self.
EXAMPLES:
sage: irr = SymmetricGroup(3).irreducible_characters()
sage: [x.values() for x in irr]
[[1, -1, 1], [2, 0, -1], [1, 1, 1]]
Return True if this group is abelian.
EXAMPLES:
sage: G = PermutationGroup(['(1,2,3)(4,5)', '(1,2,3,4,5)'])
sage: G.is_abelian()
False
sage: G = PermutationGroup(['(1,2,3)(4,5)'])
sage: G.is_abelian()
True
Return True if this group is commutative.
EXAMPLES:
sage: G = PermutationGroup(['(1,2,3)(4,5)', '(1,2,3,4,5)'])
sage: G.is_commutative()
False
sage: G = PermutationGroup(['(1,2,3)(4,5)'])
sage: G.is_commutative()
True
Return True if this group is cyclic.
EXAMPLES:
sage: G = PermutationGroup(['(1,2,3)(4,5)', '(1,2,3,4,5)'])
sage: G.is_cyclic()
False
sage: G = PermutationGroup(['(1,2,3)(4,5)'])
sage: G.is_cyclic()
True
Return True if this group is elementary abelian. An elementary
abelian group is a finite abelian group, where every nontrivial
element has order  , where
, where  is a prime.
is a prime.
EXAMPLES:
sage: G = PermutationGroup(['(1,2,3)(4,5)', '(1,2,3,4,5)'])
sage: G.is_elementary_abelian()
False
sage: G = PermutationGroup(['(1,2,3)','(4,5,6)'])
sage: G.is_elementary_abelian()
True
Return True if the groups are isomorphic.
INPUT:
OUTPUT:
EXAMPLES:
sage: v = ['(1,2,3)(4,5)', '(1,2,3,4,5)']
sage: G = PermutationGroup(v)
sage: H = PermutationGroup(['(1,2,3)(4,5)'])
sage: G.is_isomorphic(H)
False
sage: G.is_isomorphic(G)
True
sage: G.is_isomorphic(PermutationGroup(list(reversed(v))))
True
Returns True if the group is monomial. A finite group is monomial if every irreducible complex character is induced from a linear character of a subgroup.
EXAMPLES:
sage: G = PermutationGroup(['(1,2,3)(4,5)'])
sage: G.is_monomial()
True
Return True if this group is nilpotent.
EXAMPLES:
sage: G = PermutationGroup(['(1,2,3)(4,5)', '(1,2,3,4,5)'])
sage: G.is_nilpotent()
False
sage: G = PermutationGroup(['(1,2,3)(4,5)'])
sage: G.is_nilpotent()
True
Return True if this group is a normal subgroup of other.
EXAMPLES:
sage: AlternatingGroup(4).is_normal(SymmetricGroup(4))
True
sage: H = PermutationGroup(['(1,2,3)(4,5)'])
sage: G = PermutationGroup(['(1,2,3)(4,5)', '(1,2,3,4,5)'])
sage: H.is_normal(G)
False
Return True if this group is perfect. A group is perfect if it equals its derived subgroup.
EXAMPLES:
sage: G = PermutationGroup(['(1,2,3)(4,5)', '(1,2,3,4,5)'])
sage: G.is_perfect()
False
sage: G = PermutationGroup(['(1,2,3)(4,5)'])
sage: G.is_perfect()
False
Returns True if this group is a  -group. A finite group is
a
-group. A finite group is
a  -group if its order is of the form
-group if its order is of the form 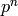 for a prime integer
for a prime integer
 and a nonnegative integer
and a nonnegative integer  .
.
EXAMPLES:
sage: G = PermutationGroup(['(1,2,3,4,5)'])
sage: G.is_pgroup()
True
Return True if this group is polycyclic. A group is polycyclic if it has a subnormal series with cyclic factors. (For finite groups, this is the same as if the group is solvable - see is_solvable.)
EXAMPLES:
sage: G = PermutationGroup(['(1,2,3)(4,5)', '(1,2,3,4,5)'])
sage: G.is_polycyclic()
False
sage: G = PermutationGroup(['(1,2,3)(4,5)'])
sage: G.is_polycyclic()
True
Returns True if the group is simple. A group is simple if it has no proper normal subgroups.
EXAMPLES:
sage: G = PermutationGroup(['(1,2,3)(4,5)'])
sage: G.is_simple()
False
Returns True if the group is solvable.
EXAMPLES:
sage: G = PermutationGroup(['(1,2,3)(4,5)'])
sage: G.is_solvable()
True
Returns True if self is a subgroup of other.
EXAMPLES:
sage: G = AlternatingGroup(5)
sage: H = SymmetricGroup(5)
sage: G.is_subgroup(H)
True
Returns True if the group is supersolvable. A finite group is supersolvable if it has a normal series with cyclic factors.
EXAMPLES:
sage: G = PermutationGroup(['(1,2,3)(4,5)'])
sage: G.is_supersolvable()
True
Return True if self is a transitive group, i.e., if the action of self on [1..n] is transitive.
EXAMPLES:
sage: G = SymmetricGroup(5)
sage: G.is_transitive()
True
sage: G = PermutationGroup(['(1,2)(3,4)(5,6)'])
sage: G.is_transitive()
False
Note that this differs from the definition in GAP, where IsTransitive returns whether the group is transitive on the set of points moved by the group.
sage: G = PermutationGroup([(2,3)])
sage: G.is_transitive()
False
sage: gap(G).IsTransitive()
true
Return an isomorphism from self to right if the groups are isomorphic, otherwise None.
INPUT:
OUTPUT:
EXAMPLES:
sage: G = PermutationGroup(['(1,2,3)(4,5)', '(1,2,3,4,5)'])
sage: H = PermutationGroup(['(1,2,3)(4,5)'])
sage: G.isomorphism_to(H) is None
True
sage: G = PermutationGroup([(1,2,3), (2,3)])
sage: H = PermutationGroup([(1,2,4), (1,4)])
sage: G.isomorphism_to(H)
Homomorphism : Permutation Group with generators [(2,3), (1,2,3)] --> Permutation Group with generators [(1,2,4), (1,4)]
If the group is simple, then this returns the name of the group.
EXAMPLES:
sage: G = CyclicPermutationGroup(5)
sage: G.isomorphism_type_info_simple_group()
rec( series := "Z", parameter := 5, name := "Z(5)" )
TESTS: This shows that the issue at trac ticket 7360 is fixed:
sage: G = KleinFourGroup()
sage: G.is_simple()
False
sage: G.isomorphism_type_info_simple_group()
...
TypeError: Group must be simple.
Return the largest point moved by a permutation in this group.
EXAMPLES:
sage: G = PermutationGroup([[(1,2),(3,4)], [(1,2,3,4)]])
sage: G.largest_moved_point()
4
sage: G = PermutationGroup([[(1,2),(3,4)], [(1,2,3,4,10)]])
sage: G.largest_moved_point()
10
sage: G = PermutationGroup([[(1,2,3),(4,5)],[(3,4)]])
sage: G.degree()
5
TODO: the name of this function is not good; this function should be deprecated in term of degree:
sage: P = PermutationGroup([[1,2,3,4]])
sage: P.largest_moved_point()
4
sage: P.cardinality()
1
Return list of all elements of this group.
EXAMPLES:
sage: G = PermutationGroup([[(1,2,3,4)], [(1,2)]])
sage: G.list()
[(), (3,4), (2,3), (2,3,4), (2,4,3), (2,4), (1,2), (1,2)(3,4), (1,2,3), (1,2,3,4), (1,2,4,3), (1,2,4), (1,3,2), (1,3,4,2), (1,3), (1,3,4), (1,3)(2,4), (1,3,2,4), (1,4,3,2), (1,4,2), (1,4,3), (1,4), (1,4,2,3), (1,4)(2,3)]
Return the lower central series of this group as a list of permutation groups.
EXAMPLES:
These computations use pseudo-random numbers, so we set the seed for reproducible testing.
sage: set_random_seed(0)
sage: G = PermutationGroup([[(1,2,3),(4,5)],[(3,4)]])
sage: G.lower_central_series() # random output
[Permutation Group with generators [(1,2,3)(4,5), (3,4)], Permutation Group with generators [(1,5)(3,4), (1,5)(2,3), (1,3)(2,4)]]
Returns the Molien series of a transitive permutation group. The function
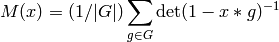
is sometimes called the “Molien series” of  . GAP’s
MolienSeries is associated to a character of a
group
. GAP’s
MolienSeries is associated to a character of a
group  . How are these related? A group
. How are these related? A group  , given as a permutation
group on
, given as a permutation
group on  points, has a “natural” representation of dimension
points, has a “natural” representation of dimension  ,
given by permutation matrices. The Molien series of
,
given by permutation matrices. The Molien series of  is the one
associated to that permutation representation of
is the one
associated to that permutation representation of  using the above
formula. Character values then count fixed points of the
corresponding permutations.
using the above
formula. Character values then count fixed points of the
corresponding permutations.
EXAMPLES:
sage: G = SymmetricGroup(5)
sage: G.molien_series()
1/(-x^15 + x^14 + x^13 - x^10 - x^9 - x^8 + x^7 + x^6 + x^5 - x^2 - x + 1)
sage: G = SymmetricGroup(3)
sage: G.molien_series()
1/(-x^6 + x^5 + x^4 - x^2 - x + 1)
Return the normal subgroups of this group as a (sorted in increasing order) list of permutation groups.
The normal subgroups of 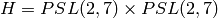 are
are
 , two copies of
, two copies of 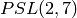 and
and 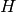 itself, as the following example shows.
itself, as the following example shows.
EXAMPLES:
sage: G = PSL(2,7)
sage: D = G.direct_product(G)
sage: H = D[0]
sage: NH = H.normal_subgroups()
sage: len(NH)
4
sage: NH[1].is_isomorphic(G)
True
sage: NH[2].is_isomorphic(G)
True
Returns the normalizer of g in self.
EXAMPLES:
sage: G = PermutationGroup([[(1,2),(3,4)], [(1,2,3,4)]])
sage: g = G([(1,3)])
sage: G.normalizer(g)
Permutation Group with generators [(2,4), (1,3)]
sage: g = G([(1,2,3,4)])
sage: G.normalizer(g)
Permutation Group with generators [(2,4), (1,2,3,4), (1,3)(2,4)]
sage: H = G.subgroup([G([(1,2,3,4)])])
sage: G.normalizer(H)
Permutation Group with generators [(2,4), (1,2,3,4), (1,3)(2,4)]
Returns True if the group other is normalized by self. Wraps GAP’s IsNormal function.
A group  normalizes a group
normalizes a group 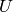 if and only if for every
if and only if for every
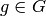 and
and 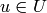 the element
the element 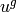 is a member of
is a member of 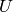 . Note that
. Note that 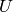 need not be a subgroup of
need not be a subgroup of  .
.
EXAMPLES:
sage: G = PermutationGroup(['(1,2,3)(4,5)'])
sage: H = PermutationGroup(['(1,2,3)(4,5)', '(1,2,3,4,5)'])
sage: H.normalizes(G)
False
sage: G = SymmetricGroup(3)
sage: H = PermutationGroup( [ (4,5,6) ] )
sage: G.normalizes(H)
True
sage: H.normalizes(G)
True
In the last example,  and
and 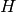 are disjoint, so each normalizes the
other.
are disjoint, so each normalizes the
other.
Return the orbit of the given integer under the group action.
EXAMPLES:
sage: G = PermutationGroup([ [(3,4)], [(1,3)] ])
sage: G.orbit(3)
[3, 4, 1]
sage: G = PermutationGroup([[(1,2),(3,4)], [(1,2,3,4,10)]])
sage: G.orbit(3)
[3, 4, 10, 1, 2]
Returns the orbits of [1,2,...,degree] under the group action.
EXAMPLES:
sage: G = PermutationGroup([ [(3,4)], [(1,3)] ])
sage: G.orbits()
[[1, 3, 4], [2]]
sage: G = PermutationGroup([[(1,2),(3,4)], [(1,2,3,4,10)]])
sage: G.orbits()
[[1, 2, 3, 4, 10], [5], [6], [7], [8], [9]]
The answer is cached:
sage: G.orbits() is G.orbits()
True
AUTHORS:
Return the number of elements of this group.
EXAMPLES:
sage: G = PermutationGroup([[(1,2,3),(4,5)], [(1,2)]])
sage: G.order()
12
sage: G = PermutationGroup([()])
sage: G.order()
1
sage: G = PermutationGroup([])
sage: G.order()
1
Returns the Poincare series of 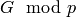 (
(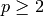 must be a
prime), for
must be a
prime), for  large. In other words, if you input a finite
group
large. In other words, if you input a finite
group  , a prime
, a prime  , and a positive integer
, and a positive integer  , it returns a
quotient of polynomials
, it returns a
quotient of polynomials 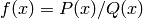 whose coefficient of
whose coefficient of
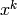 equals the rank of the vector space
equals the rank of the vector space
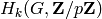 , for all
, for all  in the
range
in the
range 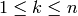 .
.
REQUIRES: GAP package HAP (in gap_packages-*.spkg).
EXAMPLES:
sage: G = SymmetricGroup(5)
sage: G.poincare_series(2,10) # optional - gap_packages
(x^2 + 1)/(x^4 - x^3 - x + 1)
sage: G = SymmetricGroup(3)
sage: G.poincare_series(2,10) # optional - gap_packages
1/(-x + 1)
AUTHORS:
Returns the quotient of this permutation group by the normal
subgroup  .
.
Wraps the GAP operator “/”.
EXAMPLES:
sage: G = PermutationGroup([(1,2,3), (2,3)])
sage: N = PermutationGroup([(1,2,3)])
sage: G.quotient(N)
Permutation Group with generators [(1,2)]
This function has been deprecated and will be removed in a future version of Sage; use quotient instead.
Original docstring follows.
Returns the quotient of this permutation group by the normal
subgroup  .
.
Wraps the GAP operator “/”.
TESTS:
sage: G = PermutationGroup([(1,2,3), (2,3)])
sage: N = PermutationGroup([(1,2,3)])
sage: G.quotient_group(N)
doctest:...: DeprecationWarning: quotient_group() is deprecated; use quotient() instead.
Permutation Group with generators [(1,2)]
Return a random element of this group.
EXAMPLES:
sage: G = PermutationGroup([[(1,2,3),(4,5)], [(1,2)]])
sage: G.random_element()
(1,2)(4,5)
Return the smallest point moved by a permutation in this group.
EXAMPLES:
sage: G = PermutationGroup([[(3,4)], [(2,3,4)]])
sage: G.smallest_moved_point()
2
sage: G = PermutationGroup([[(1,2),(3,4)], [(1,2,3,4,10)]])
sage: G.smallest_moved_point()
1
Return the subgroup of self which stabilize the given position. self and its stabilizers must have same degree.
EXAMPLES:
sage: G = PermutationGroup([ [(3,4)], [(1,3)] ])
sage: G.stabilizer(1)
Permutation Group with generators [(3,4)]
sage: G.stabilizer(3)
Permutation Group with generators [(1,4)]
sage: G = PermutationGroup([[(1,2),(3,4)], [(1,2,3,4,10)]])
sage: G.stabilizer(10)
Permutation Group with generators [(1,2)(3,4), (2,3,4)]
sage: G.stabilizer(1)
Permutation Group with generators [(2,3)(4,10), (2,10,4)]
sage: G = PermutationGroup([[(2,3,4)],[(6,7)]])
sage: G.stabilizer(1)
Permutation Group with generators [(6,7), (2,3,4)]
sage: G.stabilizer(2)
Permutation Group with generators [(6,7)]
sage: G.stabilizer(3)
Permutation Group with generators [(6,7)]
sage: G.stabilizer(4)
Permutation Group with generators [(6,7)]
sage: G.stabilizer(5)
Permutation Group with generators [(6,7), (2,3,4)]
sage: G.stabilizer(6)
Permutation Group with generators [(2,3,4)]
sage: G.stabilizer(7)
Permutation Group with generators [(2,3,4)]
sage: G.stabilizer(8)
Permutation Group with generators [(6,7), (2,3,4)]
Return a Strong Generating System of self according the given base for the right action of self on itself.
base_of_group is a list of the positions on which self acts,
in any order. The algorithm returns a list of transversals and each
transversal is a list of permutations. By default, base_of_group
is [1, 2, 3, ..., d] where  is the degree of the group.
is the degree of the group.
For base_of_group =
![[ \mathrm{pos}_1, \mathrm{pos}_2, \dots , \mathrm{pos}_d]](../../../_images/math/357a6162b2e42415315d392b5fb0b2236852b8b1.png) let
let 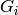 be the subgroup of
be the subgroup of  = self which stabilizes
= self which stabilizes
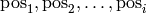 , so
, so
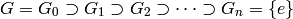
Then the algorithm returns ![[ G_i.\mathrm{transversals}(\mathrm{pos}_{i+1})]_{1 \leq i \leq n}](../../../_images/math/645f92ab9c15d2ddf436d1430277738243ea736e.png)
INPUT:
 in any order (
in any order ( is the degree of self)
is the degree of self)OUTPUT:
TESTS:
sage: G = SymmetricGroup(10)
sage: H = PermutationGroup([G.random_element() for i in range(randrange(1,3,1))])
sage: prod(map(lambda x : len(x), H.strong_generating_system()),1) == H.cardinality()
True
EXAMPLES:
sage: G = PermutationGroup([[(7,8)],[(3,4)],[(4,5)]])
sage: G.strong_generating_system()
[[()], [()], [(), (3,4,5), (3,5)], [(), (4,5)], [()], [()], [(), (7,8)], [()]]
sage: G = PermutationGroup([[(1,2,3,4)],[(1,2)]])
sage: G.strong_generating_system()
[[(), (1,2)(3,4), (1,3)(2,4), (1,4)(2,3)], [(), (2,3,4), (2,4,3)], [(), (3,4)], [()]]
sage: G = PermutationGroup([[(1,2,3)],[(4,5,7)],[(1,4,6)]])
sage: G.strong_generating_system()
[[(), (1,2,3), (1,4,6), (1,3,2), (1,5,7,4,6), (1,6,4), (1,7,5,4,6)], [(), (2,6,3), (2,3,6), (2,5,6,3)(4,7), (2,7,5,6,3), (2,4,5,6,3)], [(), (3,6)(5,7), (3,5,6), (3,7,4,5,6), (3,4,7,5,6)], [(), (4,5)(6,7), (4,7)(5,6), (4,6)(5,7)], [(), (5,6,7), (5,7,6)], [()], [()]]
sage: G = PermutationGroup([[(1,2,3)],[(2,3,4)],[(3,4,5)]])
sage: G.strong_generating_system([5,4,3,2,1])
[[(), (1,5,3,4,2), (1,5,4,3,2), (1,5)(2,3), (1,5,2)], [(), (1,3)(2,4), (1,2)(3,4), (1,4)(2,3)], [(), (1,3,2), (1,2,3)], [()], [()]]
sage: G = PermutationGroup([[(3,4)]])
sage: G.strong_generating_system()
[[()], [()], [(), (3,4)], [()]]
sage: G.strong_generating_system(base_of_group=[3,1,2,4])
[[(), (3,4)], [()], [()], [()]]
sage: G = TransitiveGroup(12,17) # optional
sage: G.strong_generating_system() # optional
[[(), (1,4,11,2)(3,6,5,8)(7,10,9,12), (1,8,3,2)(4,11,10,9)(5,12,7,6), (1,7)(2,8)(3,9)(4,10)(5,11)(6,12), (1,12,7,2)(3,10,9,8)(4,11,6,5), (1,11)(2,8)(3,5)(4,10)(6,12)(7,9), (1,10,11,8)(2,3,12,5)(4,9,6,7), (1,3)(2,8)(4,10)(5,7)(6,12)(9,11), (1,2,3,8)(4,9,10,11)(5,6,7,12), (1,6,7,8)(2,3,4,9)(5,10,11,12), (1,5,9)(3,11,7), (1,9,5)(3,7,11)], [(), (2,6,10)(4,12,8), (2,10,6)(4,8,12)], [()], [()], [()], [()], [()], [()], [()], [()], [()], [()]]
Wraps the PermutationGroup_subgroup constructor. The argument gens is a list of elements of self.
EXAMPLES:
sage: G = PermutationGroup([(1,2,3),(3,4,5)])
sage: g = G((1,2,3))
sage: G.subgroup([g])
Subgroup of Permutation Group with generators [(3,4,5), (1,2,3)] generated by [(1,2,3)]
Returns a Sylow  -subgroup of the finite group
-subgroup of the finite group  , where
, where  is a
prime. This is a
is a
prime. This is a  -subgroup of
-subgroup of  whose index in
whose index in  is coprime to
is coprime to
 . Wraps the GAP function SylowSubgroup.
. Wraps the GAP function SylowSubgroup.
EXAMPLES:
sage: G = PermutationGroup(['(1,2,3)', '(2,3)'])
sage: G.sylow_subgroup(2)
Permutation Group with generators [(2,3)]
sage: G.sylow_subgroup(5)
Permutation Group with generators [()]
If G is a permutation group acting on the set 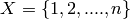 and H is the stabilizer subgroup of <integer>, a right
(respectively left) transversal is a set containing exactly
one element from each right (respectively left) coset of H. This
method returns a right transversal of self by the stabilizer
of self on <integer> position.
and H is the stabilizer subgroup of <integer>, a right
(respectively left) transversal is a set containing exactly
one element from each right (respectively left) coset of H. This
method returns a right transversal of self by the stabilizer
of self on <integer> position.
EXAMPLES:
sage: G = PermutationGroup([ [(3,4)], [(1,3)] ])
sage: G.transversals(1)
[(), (1,3,4), (1,4,3)]
sage: G = PermutationGroup([[(1,2),(3,4)], [(1,2,3,4,10)]])
sage: G.transversals(1)
[(), (1,2)(3,4), (1,3,2,10,4), (1,4,2,10,3), (1,10,4,3,2)]
Returns the trivial character of self.
EXAMPLES:
sage: SymmetricGroup(3).trivial_character()
Character of Symmetric group of order 3! as a permutation group
Return the upper central series of this group as a list of permutation groups.
EXAMPLES:
These computations use pseudo-random numbers, so we set the seed for reproducible testing.
sage: G = PermutationGroup([[(1,2,3),(4,5)],[(3,4)]])
sage: G.upper_central_series()
[Permutation Group with generators [()]]
Bases: sage.groups.perm_gps.permgroup.PermutationGroup_generic
Subgroup subclass of PermutationGroup_generic, so instance methods are inherited.
EXAMPLES:
sage: G = CyclicPermutationGroup(4)
sage: gens = G.gens()
sage: H = DihedralGroup(4)
sage: PermutationGroup_subgroup(H,list(gens))
Subgroup of Dihedral group of order 8 as a permutation group generated by [(1,2,3,4)]
sage: K=PermutationGroup_subgroup(H,list(gens))
sage: K.list()
[(), (1,2,3,4), (1,3)(2,4), (1,4,3,2)]
sage: K.ambient_group()
Dihedral group of order 8 as a permutation group
sage: K.gens()
[(1,2,3,4)]
Return the ambient group related to self.
EXAMPLES:
An example involving the dihedral group on four elements,
 :
:
sage: G = DihedralGroup(4)
sage: H = CyclicPermutationGroup(4)
sage: gens = H.gens()
sage: S = PermutationGroup_subgroup(G, list(gens))
sage: S.ambient_group()
Dihedral group of order 8 as a permutation group
sage: S.ambient_group() == G
True
Return the generators for this subgroup.
EXAMPLES:
An example involving the dihedral group on four elements,
 :
:
sage: G = DihedralGroup(4)
sage: H = CyclicPermutationGroup(4)
sage: gens = H.gens()
sage: S = PermutationGroup_subgroup(G, list(gens))
sage: S.gens()
[(1,2,3,4)]
sage: S.gens() == list(H.gens())
True
Takes the direct product of the permutation groups listed in P.
EXAMPLES:
sage: G1 = AlternatingGroup([1,2,4,5])
sage: G2 = AlternatingGroup([3,4,6,7])
sage: D = direct_product_permgroups([G1,G2,G1])
sage: D.order()
1728
sage: D = direct_product_permgroups([G1])
sage: D==G1
True
sage: direct_product_permgroups([])
Symmetric group of order 0! as a permutation group
Convert a string giving a list of GAP permutations into a list of elements of G.
EXAMPLES:
sage: from sage.groups.perm_gps.permgroup import from_gap_list
sage: G = PermutationGroup([[(1,2,3),(4,5)],[(3,4)]])
sage: L = from_gap_list(G, "[(1,2,3)(4,5), (3,4)]"); L
[(1,2,3)(4,5), (3,4)]
sage: L[0].parent() is G
True
sage: L[1].parent() is G
True
Load the GAP hap package into the default GAP interpreter interface. If this fails, try one more time to load it.
EXAMPLES:
sage: sage.groups.perm_gps.permgroup.load_hap()