Weyl Groups

AUTHORS:

• Daniel Bump (2008): initial version
• Mike Hansen (2008): initial version
• Anne Schilling (2008): initial version
• Nicolas Thiery (2008): initial version

EXAMPLES:

More examples on Weyl Groups should be added here...

The Cayley graph of the Weyl Group of type [‘A’, 3]:

sage: w = WeylGroup(['A',3])
sage: d = w.cayley_graph(); d
Digraph on 24 vertices
sage: d.show3d(color_by_label=True, edge_size=0.01, vertex_size=0.03)

The Cayley graph of the Weyl Group of type [‘D’, 4]:

sage: w = WeylGroup(['D',4])
sage: d = w.cayley_graph(); d
Digraph on 192 vertices
sage: d.show3d(color_by_label=True, edge_size=0.01, vertex_size=0.03) #long time (less than one minute)

class sage.combinat.root_system.weyl_group.ClassicalWeylSubgroup(domain, prefix)

Bases: sage.combinat.root_system.weyl_group.WeylGroup_gens

A class for Classical Weyl Subgroup of a Weyl Group

EXAMPLES:

sage: G = WeylGroup(["A",3,1]).classical()
sage: G
Parabolic Subgroup of the Weyl Group of type ['A', 3, 1] (as a matrix group acting on the root space)
sage: G.category()
Category of finite weyl groups
sage: G.cardinality()
24
sage: TestSuite(G).run()

TESTS:

sage: from sage.combinat.root_system.weyl_group import ClassicalWeylSubgroup
sage: H = ClassicalWeylSubgroup(RootSystem(["A", 3, 1]).root_space(), prefix=None)
sage: H is G
True

Caveat: the interface is likely to change. The current main application is for plots.

TODO: implement:

• Parabolic subrootsystems
• Parabolic subgroups with a set of nodes as argument

cartan_type(*args, **kwds)

EXAMPLES:

sage: WeylGroup(['A',3,1]).classical().cartan_type()
['A', 3]
sage: WeylGroup(['A',3,1]).classical().index_set()
[1, 2, 3]

Note: won’t be needed, once the lattice will be a parabolic sub root system

simple_reflections()

EXAMPLES:

sage: WeylGroup(['A',2,1]).classical().simple_reflections()
Finite family {1: [ 1  0  0]
                  [ 1 -1  1]
                  [ 0  0  1],
               2: [ 1  0  0]
                  [ 0  1  0]
                  [ 1  1 -1]}

Note: won’t be needed, once the lattice will be a parabolic sub root system

weyl_group(prefix='hereditary')

Return the Weyl group associated to the parabolic subgroup.

EXAMPLES:

sage: WeylGroup(['A',4,1]).classical().weyl_group()
Weyl Group of type ['A', 4, 1] (as a matrix group acting on the root space)
sage: WeylGroup(['C',4,1]).classical().weyl_group()
Weyl Group of type ['C', 4, 1] (as a matrix group acting on the root space)
sage: WeylGroup(['E',8,1]).classical().weyl_group()
Weyl Group of type ['E', 8, 1] (as a matrix group acting on the root space)

sage.combinat.root_system.weyl_group.WeylGroup(x, prefix=None)

Returns the Weyl group of type ct.

INPUT:

• ct - a Cartan Type.

OPTIONAL:

• prefix - changes the representation of elements from matrices to products of simple reflections

EXAMPLES: The following constructions yield the same result, namely a weight lattice and its corresponding Weyl group:

sage: G = WeylGroup(['F',4])
sage: L = G.domain()

or alternatively and equivalently:

sage: L = RootSystem(['F',4]).ambient_space()
sage: G = L.weyl_group()

Either produces a weight lattice, with access to its roots and weights.

sage: G = WeylGroup(['F',4])
sage: G.order()
1152
sage: [s1,s2,s3,s4] = G.simple_reflections()
sage: w = s1*s2*s3*s4; w
[ 1/2  1/2  1/2  1/2]
[-1/2  1/2  1/2 -1/2]
[ 1/2  1/2 -1/2 -1/2]
[ 1/2 -1/2  1/2 -1/2]
sage: type(w) == G.element_class
True
sage: w.order()
12
sage: w.length() # length function on Weyl group
4

The default representation of Weyl group elements is as matrices. If you prefer, you may specify a prefix, in which case the elements are represented as products of simple reflections.

sage: W=WeylGroup("C3",prefix="s")
sage: [s1,s2,s3]=W.simple_reflections() # lets Sage parse its own output
sage: s2*s1*s2*s3
s1*s2*s3*s1
sage: s2*s1*s2*s3 == s1*s2*s3*s1
True
sage: (s2*s3)^2==(s3*s2)^2
True
sage: (s1*s2*s3*s1).matrix()
[ 0  0 -1]
[ 0  1  0]
[ 1  0  0]

sage: L = G.domain()
sage: fw = L.fundamental_weights(); fw
Finite family {1: (1, 1, 0, 0), 2: (2, 1, 1, 0), 3: (3/2, 1/2, 1/2, 1/2), 4: (1, 0, 0, 0)}
sage: rho = sum(fw); rho
(11/2, 5/2, 3/2, 1/2)
sage: w.action(rho) # action of G on weight lattice
(5, -1, 3, 2)

TESTS:

sage: TestSuite(WeylGroup([“A”,3])).run() sage: TestSuite(WeylGroup([“A”,3, 1])).run()

sage: W=WeylGroup([‘A’,3,1]) sage: s=W.simple_reflections() sage: w=s[0]*s[1]*s[2] sage: w.reduced_word() [0, 1, 2] sage: w=s[0]*s[2] sage: w.reduced_word() [2, 0]

class sage.combinat.root_system.weyl_group.WeylGroupElement(g, parent)

Bases: sage.groups.matrix_gps.matrix_group_element.MatrixGroupElement

Class for a Weyl Group elements

action(v)

Returns the action of self on the vector v.

EXAMPLES::

sage: W = WeylGroup([‘A’,2]) sage: s = W.simple_reflections() sage: v = W.domain()([1,0,0]) sage: s[1].action(v) (0, 1, 0)

sage: W = WeylGroup(RootSystem([‘A’,2]).root_lattice()) sage: s = W.simple_reflections() sage: alpha = W.domain().simple_roots() sage: s[1].action(alpha[1]) -alpha[1]

sage: W=WeylGroup([‘A’,2,1]) sage: alpha = W.domain().simple_roots() sage: s = W.simple_reflections() sage: s[1].action(alpha[1]) -alpha[1] sage: s[1].action(alpha[0]) alpha[0] + alpha[1]

apply_simple_reflection(i, side='right')

domain()

Returns the ambient lattice associated with self.

EXAMPLES:

sage: W = WeylGroup(['A',2])
sage: s1 = W.simple_reflection(1)
sage: s1.domain()
Ambient space of the Root system of type ['A', 2]

has_descent(i, positive=False, side='right')

Tests if self has a descent at position , that is if self is on the strict negative side of the 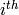simple reflection hyperplane.

If positive is True, tests if it is on the strict positive side instead.

EXAMPLES:

sage: W = WeylGroup(['A',3])
sage: s = W.simple_reflections()
sage: [W.unit().has_descent(i) for i in W.domain().index_set()]
[False, False, False]
sage: [s[1].has_descent(i) for i in W.domain().index_set()]
[True, False, False]
sage: [s[2].has_descent(i) for i in W.domain().index_set()]
[False, True, False]
sage: [s[3].has_descent(i) for i in W.domain().index_set()]
[False, False, True]
sage: [s[3].has_descent(i, True) for i in W.domain().index_set()]
[True, True, False]
sage: W = WeylGroup(['A',3,1])
sage: s = W.simple_reflections()
sage: [W.one().has_descent(i) for i in W.domain().index_set()]
[False, False, False, False]
sage: [s[0].has_descent(i) for i in W.domain().index_set()]
[True, False, False, False]
sage: w = s[0] * s[1]
sage: [w.has_descent(i) for i in W.domain().index_set()]
[False, True, False, False]
sage: [w.has_descent(i, side = "left") for i in W.domain().index_set()]
[True, False, False, False]
sage: w = s[0] * s[2]
sage: [w.has_descent(i) for i in W.domain().index_set()]
[True, False, True, False]
sage: [w.has_descent(i, side = "left") for i in W.domain().index_set()]
[True, False, True, False]

sage: W = WeylGroup(['A',3])
sage: W.one().has_descent(0)
True
sage: W.w0.has_descent(0)
False

inverse()

Returns the inverse of self.

EXAMPLES:

sage: W = WeylGroup(['A',2])
sage: w = W.unit()
sage: w = w.inverse()
sage: type(w.inverse()) == W.element_class
True
sage: W=WeylGroup(['A',2])
sage: w=W.from_reduced_word([2,1])
sage: w.inverse().reduced_word()
[1, 2]
sage: ~w == w.inverse()
True

matrix()

Returns self as a matrix.

EXAMPLES:

sage: W = WeylGroup(['A',2])
sage: s1 = W.simple_reflection(1)
sage: m = s1.matrix(); m
[0 1 0]
[1 0 0]
[0 0 1]            
sage: m.parent()
Full MatrixSpace of 3 by 3 dense matrices over Rational Field

parent()

Returns self’s parent.

EXAMPLES:

sage: W = WeylGroup(['A',2])
sage: s = W.simple_reflections()
sage: s[1].parent()
Weyl Group of type ['A', 2] (as a matrix group acting on the ambient space)

to_permutation()

A first approximation of to_permutation ...

This assumes types A,B,C,D on the ambient lattice

This further assume that the basis is indexed by 0,1,... and returns a permutation of (5,4,2,3,1) (beuargl), as a tuple

to_permutation_string()

EXAMPLES::

sage: W = WeylGroup([“A”,3]) sage: s = W.simple_reflections() sage: (s[1]*s[2]*s[3]).to_permutation_string() ‘2341’

class sage.combinat.root_system.weyl_group.WeylGroup_gens(domain, prefix)

Bases: sage.misc.cachefunc.ClearCacheOnPickle, sage.structure.unique_representation.UniqueRepresentation, sage.groups.matrix_gps.matrix_group.MatrixGroup_gens

Element

alias of WeylGroupElement

bruhat_graph(x, y)

The Bruhat graph Gamma(x,y), defined if x <= y in the Bruhat order, has as its vertices the Bruhat interval, {t | x <= t <= y}, and as its edges the pairs u, v such that u = r.v where r is a reflection, that is, a conjugate of a simple reflection.

Returns the Bruhat graph as a directed graph, with an edge u –> v if and only if u < v in the Bruhat order, and u = r.v.

See:

Carrell, The Bruhat graph of a Coxeter group, a conjecture of Deodhar, and rational smoothness of Schubert varieties. Algebraic groups and their generalizations: classical methods (University Park, PA, 1991), 53–61, Proc. Sympos. Pure Math., 56, Part 1, Amer. Math. Soc., Providence, RI, 1994.

EXAMPLES:

sage: W = WeylGroup(“A3”, prefix = “s”) sage: [s1,s2,s3] = W.simple_reflections() sage: W.bruhat_graph(s1*s3,s1*s2*s3*s2*s1) Digraph on 10 vertices

cartan_type(*args, **kwds)

Returns the CartanType associated to self.

EXAMPLES:

sage: G = WeylGroup(['F',4])
sage: G.cartan_type()
['F', 4]

character_table()

Returns the GAP character table as a string. For larger tables you may preface this with a command such as gap.eval(“SizeScreen([120,40])”) in order to widen the screen.

EXAMPLES:

sage: print WeylGroup(['A',3]).character_table()
CT1
<BLANKLINE>
     2  3  2  2  .  3
     3  1  .  .  1  .
<BLANKLINE>
       1a 4a 2a 3a 2b
<BLANKLINE>
X.1     1 -1 -1  1  1
X.2     3  1 -1  . -1
X.3     2  .  . -1  2
X.4     3 -1  1  . -1
X.5     1  1  1  1  1

classical()

If self is a Weyl group from an affine Cartan Type, this give the classical parabolic subgroup of self.

Caveat: we assume that 0 is a special node of the Dynkin diagram

TODO: extract parabolic subgroup method

domain()

Returns the domain of the element of self, that is the root lattice realization on which they act.

EXAMPLES:

sage: G = WeylGroup(['F',4])
sage: G.domain()
Ambient space of the Root system of type ['F', 4]
sage: G = WeylGroup(['A',3,1])
sage: G.domain()
Root space over the Rational Field of the Root system of type ['A', 3, 1]

This method used to be called lattice:

sage: G.lattice() doctest:...: DeprecationWarning: (Since Sage Version 4.3.4) lattice is deprecated. Please use domain instead. Root space over the Rational Field of the Root system of type [‘A’, 3, 1]

from_morphism(f)

gens()

Returns the generators of self, i.e. the simple reflections.

EXAMPLES:

sage: G = WeylGroup(['A',3])
sage: G.gens()
[[0 1 0 0]
 [1 0 0 0]
 [0 0 1 0]
 [0 0 0 1],
 [1 0 0 0]
 [0 0 1 0]
 [0 1 0 0]
 [0 0 0 1],
 [1 0 0 0]
 [0 1 0 0]
 [0 0 0 1]
 [0 0 1 0]]

index_set(*args, **kwds)

Returns the index set of self.

EXAMPLES:

sage: G = WeylGroup(['F',4])
sage: G.index_set()
[1, 2, 3, 4]
sage: G = WeylGroup(['A',3,1])
sage: G.index_set()
[0, 1, 2, 3]

lattice(*args, **kwds)

Returns the domain of the element of self, that is the root lattice realization on which they act.

EXAMPLES:

sage: G = WeylGroup(['F',4])
sage: G.domain()
Ambient space of the Root system of type ['F', 4]
sage: G = WeylGroup(['A',3,1])
sage: G.domain()
Root space over the Rational Field of the Root system of type ['A', 3, 1]

This method used to be called lattice:

sage: G.lattice() doctest:...: DeprecationWarning: (Since Sage Version 4.3.4) lattice is deprecated. Please use domain instead. Root space over the Rational Field of the Root system of type [‘A’, 3, 1]

list()

Returns a list of the elements of self.

EXAMPLES:

sage: G = WeylGroup(['A',1])
sage: G.list()
[[1 0]
 [0 1], [0 1]
 [1 0]]

This overrides the implementation of MatrixGroup_gap. Those seem typical timings (without the overriding):

# sage: W = WeylGroup([“C”,4])

# sage: %time len(W.list())

CPU times: user 7.63 s, sys: 0.60 s, total: 8.22 s Wall time: 8.63 s

# sage: %time len([ x for x in W])

CPU times: user 3.23 s, sys: 0.09 s, total: 3.32 s Wall time: 3.34 s

# sage: %time len(list(W))

CPU times: user 3.26 s, sys: 0.02 s, total: 3.28 s Wall time: 3.29 s

long_element_hardcoded()

Returns the long Weyl group element (hardcoded data)

Do we really want to keep it? There is a generic implementation which works in all cases. The hardcoded should have a better complexity (for large classical types), but there is a cache, so does this really matter?

EXAMPLES:

sage: types = [ ['A',5],['B',3],['C',3],['D',4],['G',2],['F',4],['E',6] ]
sage: [WeylGroup(t).long_element().length() for t in types]
[15, 9, 9, 12, 6, 24, 36]
sage: all( WeylGroup(t).long_element() == WeylGroup(t).long_element_hardcoded() for t in types )
True

morphism_matrix(f)

one(*args, **kwds)

Returns the unit element of the Weyl group

EXAMPLES::

sage: W = WeylGroup([‘A’,3]) sage: e = W.unit(); e [1 0 0 0] [0 1 0 0] [0 0 1 0] [0 0 0 1] sage: type(e) == W.element_class True

reflections()

The reflections of W are the conjugates of the simple reflections. They are in bijection with the positive roots, for given a positive root, we may have the reflection in the hyperplane orthogonal to it. This method returns a dictionary indexed by the reflections taking values in the positive roots. This requires self to be a finite Weyl group.

EXAMPLES:

sage: W = WeylGroup("B2",prefix="s")
sage: refdict = W.reflections(); refdict
Finite family {s1: (1, -1), s2*s1*s2: (1, 1), s1*s2*s1: (1, 0), s2: (0, 1)}
sage: [refdict[r]+r.action(refdict[r]) for r in refdict.keys()]
[(0, 0), (0, 0), (0, 0), (0, 0)]

simple_reflection(i)

Returns the 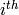simple reflection.

EXAMPLES:

sage: G = WeylGroup(['F',4])
sage: G.simple_reflection(1)
[1 0 0 0]
[0 0 1 0]
[0 1 0 0]
[0 0 0 1]
sage: W=WeylGroup(['A',2,1])
sage: W.simple_reflection(1)
[ 1  0  0]
[ 1 -1  1]
[ 0  0  1]

simple_reflections(*args, **kwds)

Returns the simple reflections of self, as a family.

EXAMPLES:

There are the simple reflections for the symmetric group:

sage: W=WeylGroup(['A',2])
sage: s = W.simple_reflections(); s
Finite family {1: [0 1 0]
[1 0 0]
[0 0 1], 2: [1 0 0]
[0 0 1]
[0 1 0]}

As a special feature, for finite irreducible root systems, s[0] gives the reflection along the highest root:

sage: s[0]
[0 0 1]
[0 1 0]
[1 0 0]

We now look at some further examples:

sage: W=WeylGroup(['A',2,1])
sage: W.simple_reflections()
Finite family {0: [-1  1  1]
[ 0  1  0]
[ 0  0  1], 1: [ 1  0  0]
[ 1 -1  1]
[ 0  0  1], 2: [ 1  0  0]
[ 0  1  0]
[ 1  1 -1]}
sage: W = WeylGroup(['F',4])
sage: [s1,s2,s3,s4] = W.simple_reflections()
sage: w = s1*s2*s3*s4; w
[ 1/2  1/2  1/2  1/2]
[-1/2  1/2  1/2 -1/2]
[ 1/2  1/2 -1/2 -1/2]
[ 1/2 -1/2  1/2 -1/2]
sage: s4^2 == W.unit()
True
sage: type(w) == W.element_class
True

unit(*args, **kwds)

Returns the unit element of the Weyl group

EXAMPLES::

sage: W = WeylGroup([‘A’,3]) sage: e = W.unit(); e [1 0 0 0] [0 1 0 0] [0 0 1 0] [0 0 0 1] sage: type(e) == W.element_class True