Weyl Characters¶

class sage.combinat.root_system.weyl_characters.WeightRing(A, prefix=None)¶

Bases: sage.rings.ring.Algebra

base_ring()¶

Returns the base ring.

EXAMPLES:

sage: R = WeylCharacterRing(['A',3], base_ring = CC); R.base_ring()
Complex Field with 53 bits of precision

cartan_type()¶

Returns the Cartan type.

EXAMPLES:

sage: A2 = WeylCharacterRing("A2")
sage: WeightRing(A2).cartan_type()
['A', 2]

fundamental_weights()¶

Returns the fundamental weights.

EXAMPLES:

sage: WeightRing(WeylCharacterRing("G2")).fundamental_weights()
Finite family {1: (1, 0, -1), 2: (2, -1, -1)}

positive_roots()¶

Returns the positive roots.

EXAMPLES:

sage: WeightRing(WeylCharacterRing("G2")).positive_roots()
[(0, 1, -1), (1, -2, 1), (1, -1, 0), (1, 0, -1), (1, 1, -2), (2, -1, -1)]

simple_roots()¶

Returns the simple roots.

EXAMPLES:

sage: WeightRing(WeylCharacterRing("G2")).simple_roots()
Finite family {1: (0, 1, -1), 2: (1, -2, 1)}

space()¶

Returns the weight space realization associated to self.

EXAMPLES:

sage: E8 = WeylCharacterRing(['E',8])
sage: e8 = WeightRing(E8)
sage: e8.space()
Ambient space of the Root system of type ['E', 8]

wt_repr(wt)¶

Returns a string representing the irreducible character with highest weight vectr wt.

EXAMPLES:

sage: G2 = WeylCharacterRing(['G',2])
sage: g2 = WeightRing(G2)
sage: g2.wt_repr([1,0,0])
'g2(1,0,0)'

class sage.combinat.root_system.weyl_characters.WeightRingElement(A, mdict)¶

Bases: sage.structure.element.AlgebraElement

A class for weights, and linear combinations of weights. See WeightRing? for more information.

cartan_type()¶

Returns the Cartan type.

EXAMPLES:

sage: A2=WeylCharacterRing("A2")
sage: a2 = WeightRing(A2)
sage: a2([0,1,0]).cartan_type()
['A', 2]

character()¶

Assuming that self is invariant under the Weyl group, this will express it as a linear combination of characters. If self is not Weyl group invariant, this method will not terminate.

EXAMPLES:

sage: A2 = WeylCharacterRing(['A',2])
sage: a2 = WeightRing(A2)
sage: W = a2.space().weyl_group()
sage: mu = a2(2,1,0)
sage: nu = sum(mu.weyl_group_action(w) for w in W)
sage: nu
a2(0,1,2) + a2(0,2,1) + a2(1,0,2) + a2(1,2,0) + a2(2,0,1) + a2(2,1,0)
sage: nu.character()
-2*A2(1,1,1) + A2(2,1,0)

mlist()¶

Returns a list of weights in self with their multiplicities.

EXAMPLES:

sage: G2 = WeylCharacterRing(['G',2])
sage: g2 = WeightRing(G2)
sage: pr = sum(g2(a) for a in G2.positive_roots())
sage: sorted(pr.mlist())
[[(1, -2, 1), 1],  [(1, -1, 0), 1],  [(1, 1, -2), 1],  [(1, 0, -1), 1],  [(2, -1, -1), 1],  [(0, 1, -1), 1]]

weyl_group_action(w)¶

Returns the actionof the Weyl group element w on self.

EXAMPLES:

sage: G2 = WeylCharacterRing(['G',2])
sage: g2 = WeightRing(G2)
sage: L = g2.space()
sage: [fw1, fw2] = L.fundamental_weights()
sage: sum(g2(fw2).weyl_group_action(w) for w in L.weyl_group())
2*g2(-2,1,1) + 2*g2(-1,-1,2) + 2*g2(-1,2,-1) + 2*g2(1,-2,1) + 2*g2(1,1,-2) + 2*g2(2,-1,-1)

class sage.combinat.root_system.weyl_characters.WeylCharacter(A, hdict, mdict)¶

Bases: sage.structure.element.AlgebraElement

A class for Weyl Characters. Let K be a compact Lie group, which we assume is semisimple and simply-connected. Its complexified Lie algebra L is the Lie algebra of a complex analytic Lie group G. The following three categories are equivalent: representations of K; representations of L; and analytic representations of G. In every case, there is a parametrization of the irreducible representations by their highest weight vectors. For this theory of Weyl, see (for example) J. F. Adams, Lectures on Lie groups; Broecker and Tom Dieck, Representations of Compact Lie groups; Bump, Lie Groups, Part I; Fulton and Harris, Representation Theory, Part IV; Goodman and Wallach, Representations and Invariants of the Classical Groups, Chapter 5; Hall, Lie Groups, Lie Algebras and Representations; Humphreys, Introduction to Lie Algebras and their representations; Procesi, Lie Groups; Samelson, Notes on Lie Algebras; Varadarajan, Lie groups, Lie algebras, and their representations; or Zhelobenko, Compact Lie Groups and their Representations.

Computations that you can do with these include computing their weight multiplicities, products (thus decomposing the tensor product of a representation into irreducibles) and branching rules (restriction to a smaller group).

There is associated with K, L or G as above a lattice, the weight lattice, whose elements (called weights) are characters of a Cartan subgroup or subalgebra. There is an action of the Weyl group W on the lattice, and elements of a fixed fundamental domain for W, the positive Weyl chamber, are called dominant. There is for each representation a unique highest dominant weight that occurs with nonzero multiplicity with respect to a certain partial order, and it is called the highest weight vector.

EXAMPLES:

sage: L = RootSystem("A2").ambient_space()
sage: [fw1,fw2] = L.fundamental_weights()
sage: R = WeylCharacterRing(['A',2], prefix="R")
sage: [R(1),R(fw1),R(fw2)]
[R(0,0,0), R(1,0,0), R(1,1,0)]

Here R(1), R(fw1) and R(fw2) are irreducible representations with highest weight vectors 0, and the first two fundamental weights.

A Weyl character is a character (not necessarily irreducible) of a reductive Lie group or algebra. It is represented by a pair of dictionaries. The mdict is a dictionary of weight multiplicities. The hdict is a dictionary of highest weight vectors of the irreducible characters that occur in its decomposition into irreducibles, with the multiplicities in this decomposition.

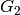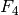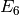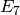For type A (also $G_2$ , $F_4$ , $E_6$ and $E_7$ ) we will take as the weight lattice not the weight lattice of the semisimple group, but for a larger one. For type A, this means we are concerned with the representation theory of K=U(n) or G=GL(n,CC) rather than SU(n) or SU(n,CC). This is useful since the representation theory of GL(n) is ubiquitous, and also since we may then represent the fundamental weights (in root_system.py) by vectors with integer entries. If you are only interested in SL(3), say, use WeylCharacterRing([‘A’,2]) as above but be aware that R([a,b,c]) and R([a+1,b+1,c+1]) represent the same character of SL(3) since R([1,1,1]) is the determinant.

branch(S, rule='default')¶

Returns the restriction of the character to the subalgebra. If no rule is specified, we will try to specify one.

INPUT:

S - a Weyl character ring for a Lie subgroup or subalgebra

rule - a branching rule.

See branch_weyl_character? for more information about branching rules.

EXAMPLES:

sage: B3 = WeylCharacterRing(['B',3])
sage: A2 = WeylCharacterRing(['A',2])
sage: [B3(w).branch(A2,rule="levi") for w in B3.fundamental_weights()]
[A2(0,0,-1) + A2(0,0,0) + A2(1,0,0),
 A2(0,-1,-1) + A2(0,0,-1) + A2(0,0,0) + A2(1,0,-1) + A2(1,0,0) + A2(1,1,0),
 A2(-1/2,-1/2,-1/2) + A2(1/2,-1/2,-1/2) + A2(1/2,1/2,-1/2) + A2(1/2,1/2,1/2)]

cartan_type()¶

Returns the Cartan type.

EXAMPLES:

sage: A2=WeylCharacterRing("A2")
sage: A2([1,0,0]).cartan_type()
['A', 2]

check(verbose=False)¶

To check the correctness of an element, we compare the theoretical dimension computed Weyl character formula with the actual one obtained by adding up the multiplicities.

EXAMPLES:

sage: B4 = WeylCharacterRing("B4")
sage: [B4(x).check(verbose = true) for x in B4.fundamental_weights()]
[[9, 9], [36, 36], [84, 84], [16, 16]]

degree()¶

The degree of the character, that is, the dimension of module.

EXAMPLES:

sage: B3 = WeylCharacterRing(['B',3])
sage: [B3(x).degree() for x in B3.fundamental_weights()]
[7, 21, 8]

exterior_square()¶

Returns the exterior square of the character.

EXAMPLES:

sage: A2 = WeylCharacterRing("A2",style="coroots")
sage: A2(1,0).exterior_square()
A2(0,1)

frobenius_schur_indicator()¶

Returns:

$1$ if the representation is real (orthogonal)

$-1$ if the representation is quaternionic (symplectic)

$0$ if the representation is complex (not self dual)

The Frobenius-Schur indicator of a character ‘chi’ of a compact group G is the Haar integral over the group of ‘chi(g^2)’. Its value is 1,-1 or 0. This method computes it for irreducible characters of compact Lie groups by checking whether the symmetric and exterior square characters contain the trivial character.

EXAMPLES:

sage: B2 = WeylCharacterRing("B2",style="coroots")
sage: B2(1,0).frobenius_schur_indicator()
 1
sage: B2(0,1).frobenius_schur_indicator()
 -1

hlist()¶

Returns a list of highest weight vectors and multiplicities of the irreducible characters in self.

EXAMPLES:

sage: B3 = WeylCharacterRing(['B',3])
sage: B3(1/2,1/2,1/2).hlist()
[[(1/2, 1/2, 1/2), 1]]

is_irreducible()¶

Returns True if self is an irreducible character.

EXAMPLES:

sage: B3 = WeylCharacterRing(['B',3])
sage: [B3(x).is_irreducible() for x in B3.fundamental_weights()]
[True, True, True]
sage: sum(B3(x) for x in B3.fundamental_weights()).is_irreducible()
False

mlist()¶

Returns a list of weights in self with their multiplicities.

EXAMPLES:

sage: B3 = WeylCharacterRing(['B',3])
sage: sorted(B3(1/2,1/2,1/2).mlist())
[[(-1/2, -1/2, -1/2), 1],  [(-1/2, -1/2, 1/2), 1],  [(-1/2, 1/2, -1/2), 1],  [(-1/2, 1/2, 1/2), 1],  [(1/2, -1/2, -1/2), 1],  [(1/2, -1/2, 1/2), 1],  [(1/2, 1/2, -1/2), 1],  [(1/2, 1/2, 1/2), 1]]

parent()¶

EXAMPLES:

sage: B3 = WeylCharacterRing(['B',3])
sage: B3(2).parent()
The Weyl Character Ring of Type ['B', 3] with Integer Ring coefficients

symmetric_square()¶

Returns the symmetric square of the character.

EXAMPLES:

sage: A2 = WeylCharacterRing("A2",style="coroots")
sage: A2(1,0).symmetric_square()
A2(2,0)

sage.combinat.root_system.weyl_characters.WeylCharacterRing(ct, base_ring=Integer Ring, prefix=None, cache=False, style='lattice')¶

A class for rings of Weyl characters. The Weyl character is a character of a semisimple (or reductive) Lie group or algebra. They form a ring, in which the addition and multiplication correspond to direct sum and tensor product of representations.

INPUT:

ct – The Cartan Type

OPTIONAL ARGUMENTS:

base_ring – (default: $\ZZ$ )
prefix – (default: an automatically generated prefix based on Cartan type)
cache – (default False) setting cache = True is a substantial speedup at the expense of some memory.
style – (default “lattice”) can be set style = “coroots” to obtain an alternative representation of the elements.

If no prefix specified, one is generated based on the Cartan type. It is good to name the ring after the prefix, since then it can parse its own output.

EXAMPLES:

sage: G2 = WeylCharacterRing(['G',2])
sage: [fw1,fw2] = G2.fundamental_weights()
sage: 2*G2(2*fw1+fw2)
2*G2(4,-1,-3)
sage: 2*G2(4,-1,-3)
2*G2(4,-1,-3)
sage: G2(4,-1,-3).degree()
189

Note that since the ring was named 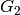$G_2$ after its default prefix, it was able to parse its own output. You do not have to use the default prefix. Thus:

EXAMPLES:

sage: R = WeylCharacterRing(['B',3], prefix='R')
sage: chi = R(R.fundamental_weights()[3]); chi
R(1/2,1/2,1/2)
sage: R(1/2,1/2,1/2) == chi
True

You may choose an alternative style of labeling the elements. If you create the ring with the option style=”coroots” then the integers in the label are not the components of the highest weight vector, but rather the coefficients when the highest weight vector is decomposed into a product of irreducibles. These coefficients are the values of the coroots on the highest weight vector.

In the coroot style the Lie group or Lie algebra is treated as semisimple, so you lose the distinction between GL(n) and SL(n); you also lose some information about representations of E6 and E7 for the same reason. The coroot style gives you output that is comparable to that in Tables of Dimensions, Indices and Branching Rules for Representations of Simple Lie Algebras (Marcel Dekker, 1981).

EXAMPLES:

sage: B3 = WeylCharacterRing("B3",style="coroots")
sage: [fw1,fw2,fw3]=B3.fundamental_weights()
sage: fw1+fw3
(3/2, 1/2, 1/2)
sage: B3(fw1+fw3)
B3(1,0,1)
sage: B3(1,0,1)
B3(1,0,1)

For type [‘A’,r], the coroot representation carries less information, since elements of the weight lattice that are orthogonal to the coroots are represented as zero. This means that with the default style you can represent the determinant, but not in the coroot style. In the coroot style, elements of the Weyl character ring represent characters of SL(r+1,CC), while in the default style, they represent characters of GL(r+1,CC).

EXAMPLES:

sage: A2 = WeylCharacterRing("A2")
sage: L = A2.space()
sage: [A2(L.det()), A2(L(0))]
[A2(1,1,1), A2(0,0,0)]
sage: A2(L.det()) == A2(L(0))
False
sage: A2 = WeylCharacterRing("A2", style="coroots")
sage: [A2(L.det()), A2(L(0))]
[A2(0,0), A2(0,0)]
sage: A2(L.det()) == A2(L(0))
True

The multiplication in a Weyl character ring corresponds to the product of characters, which you can use to determine the decomposition of tensor products into irreducibles. For example, let us compute the tensor product of the standard and spin representations of Spin(7).

EXAMPLES:

sage: B3 = WeylCharacterRing("B3")
sage: [fw1,fw2,fw3]=B3.fundamental_weights()
sage: [B3(fw1).degree(),B3(fw3).degree()]
[7, 8]
sage: B3(fw1)*B3(fw3)
B3(1/2,1/2,1/2) + B3(3/2,1/2,1/2)

The name of the irreducible representation encodes the highest weight vector.

TESTS:

sage: F4 = WeylCharacterRing(['F',4], cache = True)
sage: [fw1,fw2,fw3,fw4] = F4.fundamental_weights()
sage: chi = F4(fw4); chi, chi.degree()
(F4(1,0,0,0), 26)
sage: chi^2
F4(0,0,0,0) + F4(1,0,0,0) + F4(1,1,0,0) + F4(3/2,1/2,1/2,1/2) + F4(2,0,0,0)
sage: [x.degree() for x in [F4(0,0,0,0), F4(1,0,0,0), F4(1,1,0,0), F4(3/2,1/2,1/2,1/2), F4(2,0,0,0)]]
[1, 26, 52, 273, 324]

You can produce a list of the irreducible elements of an irreducible character.

EXAMPLES:

sage: R = WeylCharacterRing(['A',2], prefix = R)
sage: sorted(R([2,1,0]).mlist())
[[(1, 1, 1), 2],  [(1, 2, 0), 1],  [(1, 0, 2), 1],  [(2, 1, 0), 1],  [(2, 0, 1), 1],  [(0, 1, 2), 1],  [(0, 2, 1), 1]]

class sage.combinat.root_system.weyl_characters.WeylCharacterRing_class(ct, base_ring, prefix, cache, style)¶

Bases: sage.rings.ring.Algebra

base_ring()¶

Returns the base ring.

EXAMPLES:

sage: R = WeylCharacterRing(['A',3], base_ring = CC); R.base_ring()
Complex Field with 53 bits of precision

cartan_type()¶

Returns the Cartan type.

EXAMPLES:

sage: WeylCharacterRing("A2").cartan_type()
['A', 2]

char_from_weights(mdict)¶

Return the hdict given just a dictionary of weight multiplicities.

This will not terminate unless the dictionary of weight multiplicities is Weyl group invariant.

EXAMPLES:

sage: B3 = WeylCharacterRing(['B',3])
sage: m = B3(1,0,0)._mdict
sage: B3.char_from_weights(m)
{(1, 0, 0): 1}

coerce_to_e6(x)¶: For type E7 or E8, orthogonally projects an element of the root lattice into the E6 root lattice. This operation on weights corresponds to intersection with the semisimple subgroup E7.

coerce_to_e7(x)¶: For type E8, this orthogonally projects an element of the E8 root lattice into the E7 root lattice. This operation on weights corresponds to intersection with the semisimple subgroup E7.

coerce_to_sl(x)¶

For type [‘A’,r], this coerces an element of the ambient space into the root space by orthogonal projection. The root space has codimension one and corresponds to the Lie algebra of SL(r+1,CC), whereas the full weight space corresponds to the Lie algebra of GL(r+1,CC). So this operation corresponds to multiplication by a (possibly fractional) power of the determinant to give a weight determinant one.

EXAMPLES:

sage: A2=WeylCharacterRing("A2")
sage: [A2.coerce_to_sl(fw) for fw in A2.fundamental_weights()]
[(2/3, -1/3, -1/3), (1/3, 1/3, -2/3)]

dynkin_diagram()¶

Returns the Dynkin diagram.

EXAMPLES:

sage: WeylCharacterRing("E7").dynkin_diagram()
        O 2
        |
        |
O---O---O---O---O---O
1   3   4   5   6   7   
E7

extended_dynkin_diagram()¶

Returns the extended Dynkin diagram, which is the Dynkin diagram of the corresponding untwisted affine type.

EXAMPLES:

sage: WeylCharacterRing("E7").extended_dynkin_diagram()
            O 2
            |
            |
O---O---O---O---O---O---O
0   1   3   4   5   6   7
E7~

fundamental_weights()¶

Returns the fundamental weights.

EXAMPLES:

sage: WeylCharacterRing("G2").fundamental_weights()
Finite family {1: (1, 0, -1), 2: (2, -1, -1)}

highest_root()¶

Returns the highest_root.

EXAMPLES:

sage: WeylCharacterRing("G2").highest_root()
 (2, -1, -1)

irr_repr(hwv)¶

Return a string representing the irreducible character with highest weight vector hwv.

EXAMPLES:

sage: B3 = WeylCharacterRing("B3")
sage: [B3.irr_repr(v) for v in B3.fundamental_weights()]
['B3(1,0,0)', 'B3(1,1,0)', 'B3(1/2,1/2,1/2)']
sage: B3 = WeylCharacterRing("B3", style="coroots")
sage: [B3.irr_repr(v) for v in B3.fundamental_weights()]
['B3(1,0,0)', 'B3(0,1,0)', 'B3(0,0,1)']

positive_roots()¶

Returns the positive roots.

EXAMPLES:

sage: WeylCharacterRing("G2").positive_roots()
[(0, 1, -1), (1, -2, 1), (1, -1, 0), (1, 0, -1), (1, 1, -2), (2, -1, -1)]

rank()¶

Returns the rank.

EXAMPLES:

sage: WeylCharacterRing("G2").rank()
2

simple_coroots()¶

Returns the simple coroots.

EXAMPLES:

sage: WeylCharacterRing("G2").simple_roots()
Finite family {1: (0, 1, -1), 2: (1, -2, 1)}

simple_roots()¶

Returns the simple roots.

EXAMPLES:

sage: WeylCharacterRing("G2").simple_roots()
Finite family {1: (0, 1, -1), 2: (1, -2, 1)}

space()¶

Returns the weight space associated to self.

EXAMPLES:

sage: WeylCharacterRing(['E',8]).space()
Ambient space of the Root system of type ['E', 8]

sage.combinat.root_system.weyl_characters.branch_weyl_character(chi, R, S, rule='default')¶

A Branching rule describes the restriction of representations from a Lie group or algebra G to a smaller one. See for example, R. C. King, Branching rules for classical Lie groups using tensor and spinor methods. J. Phys. A 8 (1975), 429-449, Howe, Tan and Willenbring, Stable branching rules for classical symmetric pairs, Trans. Amer. Math. Soc. 357 (2005), no. 4, 1601-1626, McKay and Patera, Tables of Dimensions, Indices and Branching Rules for Representations of Simple Lie Algebras (Marcel Dekker, 1981), and Fauser, Jarvis, King and Wybourne, New branching rules induced by plethysm. J. Phys. A 39 (2006), no. 11, 2611–2655.

INPUT:

chi - a character of G
R - the Weyl Character Ring of G
S - the Weyl Character Ring of H
rule - a set of r dominant weights in H where r is the rank of G.

You may use a predefined rule by specifying rule = one of”levi”, “automorphic”, “symmetric”, “extended”, “orthogonal_sum”, “tensor”, “triality” or “miscellaneous”. The use of these rules will be explained next. After the examples we will explain how to write your own branching rules for cases that we have omitted.

To explain the predefined rules we survey the most important branching rules. These may be classified into several cases, and once this is understood, the detailed classification can be read off from the Dynkin diagrams. Dynkin classified the maximal subgroups of Lie groups in Mat. Sbornik N.S. 30(72):349-462 (1952).

We will list give predefined rules that cover most cases where the branching rule is to a maximal subgroup. For convenience, we also give some branching rules to subgroups that are not maximal. For example, a Levi subgroup may or may not be maximal.

LEVI TYPE. These can be read off from the Dynkin diagram. If removing a node from the Dynkin diagram produces another Dynkin diagram, there is a branching rule. Currently we require that the smaller diagram be connected. For these rules use the option rule=”levi”:

['A',r] => ['A',r-1]
['B',r] => ['A',r-1]
['B',r] => ['B',r-1]
['C',r] => ['A',r-1]
['C',r] => ['C',r-1]
['D',r] => ['A',r-1]
['D',r] => ['D',r-1]
['E',r] => ['A',r-1] r = 7,8
['E',r] => ['D',r-1] r = 6,7,8
['E',r] => ['E',r-1]
F4 => B3
F4 => C3
G2 => A1 (short root)

Not all Levi subgroups are maximal subgroups. If the Levi is not maximal there may or may not be a preprogrammed rule=”levi” for it. If there is not, the branching rule may still be obtained by going through an intermediate subgroup that is maximal using rule=”extended”. Thus the other Levi branching rule from G2 => A1 corresponding to the long root is available by first branching G2 => A_2 then A2 => A1. Similarly the branching rules to the Levi subgroup:

['E',r] => ['A',r-1] r = 6,7,8

may be obtained by first branching E6=>A5xA1, E7=>A7 or E8=>A8.

AUTOMORPHIC TYPE. If the Dynkin diagram has a symmetry, then there is an automorphism that is a special case of a branching rule. There is also an exotic “triality” automorphism of D4 having order 3. Use rule=”automorphic” or (for D4) rule=”triality”:

['A',r] => ['A',r]
['D',r] => ['D',r]
E6 => E6

SYMMETRIC TYPE. Related to the automorphic type, when G admits an outer automorphism (usually of degree 2) we may consider the branching rule to the isotropy subgroup H. In many cases the Dynkin diagram of H can be obtained by folding the Dynkin diagram of G. For such isotropy subgroups use rule=”symmetric”. The last branching rule, D4=>G2 is not to a maximal subgroup since D4=>B3=>G2, but it is included for convenience.

['A',2r+1] => ['B',r]
['A',2r] => ['C',r]
['A',2r] => ['D',r]
['D',r] => ['B',r-1]
E6 => F4
D4 => G2

EXTENDED TYPE. If removing a node from the extended Dynkin diagram results in a Dynkin diagram, then there is a branching rule. Use rule=”extended” for these. We will also use this classification for some rules that are not of this type, mainly involving type B, such as D6 => B3xB3.

Here is the extended Dynkin diagram for D6:

    0       6
    O       O
    |       |
    |       |
O---O---O---O---O
1   2   3   4   6

Removing the node 3 results in an embedding D3xD3 -> D6. This corresponds to the embedding SO(6)xSO(6) -> SO(12), and is of extended type. On the other hand the embedding SO(5)xSO(7)–>SO(12) (e.g. B2xB3 -> D6) cannot be explained this way but for uniformity is implemented under rule=”extended”.

The following rules are implemented as special cases of rule=”extended”.

E6 => A5xA1, A2xA2xA2
E7 => A7, D6xA1, A3xA3xA1
E8 => A8, D8, E7xA1, A4xA4, D5xA3, E6xA2
F4 => B4, C3xA1, A2xA2, A3xA1
G2 => A1xA1

Note that E8 has only a limited number of representations of reasonably low degree.

ORTHOGONAL_SUM:

Using rule=”orthogonal_sum” you can get any branching rule SO(n) => SO(a) x SO(b) x SO(c) x ... where n = a+b+c+ ... Sp(2n) => Sp(2a) x Sp(2b) x Sp(2c) x ... where n = a+b+c+ ... where O(a) = [‘D’,r] (a=2r) or [‘B’,r] (a=2r+1) and Sp(2r)=[‘C’,r]. In some cases these are also of extended type, as in the case D3xD3->D6 discussed above. But in other cases, for example B3xB3->D7, they are not of extended type.

TENSOR: There are branching rules:

['A', rs-1] => ['A',r-1] x ['A',s-1] 
['B',2rs+r+s] => ['B',r] x ['B',s]
['D',2rs+s] => ['B',r] x ['D',s]
['D',2rs] => ['D',r] x ['D',s]
['D',2rs] => ['C',r] x ['C',s]
['C',2rs+s] => ['B',r] x ['C',s]
['C',2rs] => ['C',r] x ['D',s].

corresponding to the tensor product homomorphism. For type A, the homomorphism is GL(r) x GL(s) -> GL(rs). For the classical types, the relevant fact is that if V,W are orthogonal or symplectic spaces, that is, spaces endowed with symmetric or skew-symmetric bilinear forms, then V tensor W is also an orthogonal space (if V and W are both orthogonal or both symplectic) or symplectic (if one of V and W is orthogonal and the other symplectic).

The corresponding branching rules are obtained using rule=”tensor”.

SYMMETRIC POWER: The k-th symmetric and exterior power homomorphisms map GL(n) –> GL(binomial(n+k-1,k)) and GL(binomial(n,k)). The corresponding branching rules are not implemented but a special case is. The k-th symmetric power homomorphism SL(2) –> GL(k+1) has its image inside of SO(2r+1) if k=2r and inside of Sp(2r) if k=2r-1. Hence there are branching rules:

['B',r] => A1
['C',r] => A1

and these may be obtained using the rule “symmetric_power”.

MISCELLANEOUS: Use rule=”miscellaneous” for the following rules:

B3 => G2
F4 => G2xA1 (not implemented yet)

BRANCHING RULES FROM PLETHYSMS

Nearly all branching rules G => H where G is of type A,B,C or D are covered by the preceding rules. The function branching_rules_from_plethysm covers the remaining cases.

ISOMORPHIC TYPE: Although not usually referred to as a branching rule, the effects of the accidental isomorphisms may be handled using rule=”isomorphic”:

B2 => C2
C2 => B2
A3 => D3
D3 => A3
D2 => A1xA1
B1 => A1
C1 => A1

EXAMPLES: (Levi type)

sage: A1 = WeylCharacterRing("A1")
sage: A2 = WeylCharacterRing("A2")
sage: A3 = WeylCharacterRing("A3")
sage: A4 = WeylCharacterRing("A4")
sage: A5 = WeylCharacterRing("A5")
sage: B2 = WeylCharacterRing("B2")
sage: B3 = WeylCharacterRing("B3")
sage: B4 = WeylCharacterRing("B4")
sage: C2 = WeylCharacterRing("C2")
sage: C3 = WeylCharacterRing("C3")
sage: D3 = WeylCharacterRing("D3")
sage: D4 = WeylCharacterRing("D4")
sage: D5 = WeylCharacterRing("D5")
sage: G2 = WeylCharacterRing("G2")
sage: F4 = WeylCharacterRing("F4",style="coroots")
sage: E6=WeylCharacterRing("E6",style="coroots")
sage: D5=WeylCharacterRing("D5",style="coroots")
sage: [B3(w).branch(A2,rule="levi") for w in B3.fundamental_weights()]
[A2(0,0,-1) + A2(0,0,0) + A2(1,0,0),
 A2(0,-1,-1) + A2(0,0,-1) + A2(0,0,0) + A2(1,0,-1) + A2(1,0,0) + A2(1,1,0),
 A2(-1/2,-1/2,-1/2) + A2(1/2,-1/2,-1/2) + A2(1/2,1/2,-1/2) + A2(1/2,1/2,1/2)]

The last example must be understood as follows. The representation of B3 being branched is spin, which is not a representation of SO(7) but of its double cover spin(7). The group A2 is really GL(3) and the double cover of SO(7) induces a cover of GL(3) that is trivial over SL(3) but not over the center of GL(3). The weight lattice for this GL(3) consists of triples (a,b,c) of half integers such that a-b and b-c are in 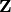$\ZZ$ , and this is reflected in the last decomposition.

sage: [C3(w).branch(A2,rule="levi") for w in C3.fundamental_weights()]
[A2(0,0,-1) + A2(1,0,0),
 A2(0,-1,-1) + A2(1,0,-1) + A2(1,1,0),
 A2(-1,-1,-1) + A2(1,-1,-1) + A2(1,1,-1) + A2(1,1,1)]
sage: [D4(w).branch(A3,rule="levi") for w in D4.fundamental_weights()]
[A3(0,0,0,-1) + A3(1,0,0,0),
 A3(0,0,-1,-1) + A3(0,0,0,0) + A3(1,0,0,-1) + A3(1,1,0,0),
 A3(1/2,-1/2,-1/2,-1/2) + A3(1/2,1/2,1/2,-1/2),
 A3(-1/2,-1/2,-1/2,-1/2) + A3(1/2,1/2,-1/2,-1/2) + A3(1/2,1/2,1/2,1/2)]
sage: [B3(w).branch(B2,rule="levi") for w in B3.fundamental_weights()]
[2*B2(0,0) + B2(1,0), B2(0,0) + 2*B2(1,0) + B2(1,1), 2*B2(1/2,1/2)]
sage: C3 = WeylCharacterRing(['C',3])
sage: [C3(w).branch(C2,rule="levi") for w in C3.fundamental_weights()]
[2*C2(0,0) + C2(1,0),
 C2(0,0) + 2*C2(1,0) + C2(1,1),
 C2(1,0) + 2*C2(1,1)]
sage: [D5(w).branch(D4,rule="levi") for w in D5.fundamental_weights()]
[2*D4(0,0,0,0) + D4(1,0,0,0),
 D4(0,0,0,0) + 2*D4(1,0,0,0) + D4(1,1,0,0),
 D4(1,0,0,0) + 2*D4(1,1,0,0) + D4(1,1,1,0),
 D4(1/2,1/2,1/2,-1/2) + D4(1/2,1/2,1/2,1/2),
 D4(1/2,1/2,1/2,-1/2) + D4(1/2,1/2,1/2,1/2)]
sage: G2(1,0,-1).branch(A1,rule="levi")
 A1(0,-1) + A1(1,-1) + A1(1,0)
sage: E6=WeylCharacterRing("E6",style="coroots")
sage: D5=WeylCharacterRing("D5",style="coroots")
sage: fw = E6.fundamental_weights()
sage: [E6(fw[i]).branch(D5,rule="levi") for i in [1,2,6]] # long time (3s)
[D5(0,0,0,0,0) + D5(0,0,0,0,1) + D5(1,0,0,0,0),
 D5(0,0,0,0,0) + D5(0,0,0,1,0) + D5(0,0,0,0,1) + D5(0,1,0,0,0),
 D5(0,0,0,0,0) + D5(0,0,0,1,0) + D5(1,0,0,0,0)]
sage: E7=WeylCharacterRing("E7",style="coroots")
sage: D6=WeylCharacterRing("D6",style="coroots")
sage: fw = E7.fundamental_weights()
sage: [E7(fw[i]).branch(D6,rule="levi") for i in [1,2,7]] # long time (26s)
[3*D6(0,0,0,0,0,0) + 2*D6(0,0,0,0,1,0) + D6(0,1,0,0,0,0),
 3*D6(0,0,0,0,0,1) + 2*D6(1,0,0,0,0,0) + 2*D6(0,0,1,0,0,0) + D6(1,0,0,0,1,0),
 D6(0,0,0,0,0,1) + 2*D6(1,0,0,0,0,0)]
sage: D7=WeylCharacterRing("D7",style="coroots",cache=True)
sage: E8=WeylCharacterRing("E8",style="coroots",cache=True)
sage: D7=WeylCharacterRing("D7",style="coroots",cache=True)
sage: E8(1,0,0,0,0,0,0,0).branch(D7,rule="levi") # not tested (very long time) (160s)
 3*D7(0,0,0,0,0,0,0) + 2*D7(0,0,0,0,0,1,0) + 2*D7(0,0,0,0,0,0,1) + 2*D7(1,0,0,0,0,0,0)
 + D7(0,1,0,0,0,0,0) + 2*D7(0,0,1,0,0,0,0) + D7(0,0,0,1,0,0,0) + D7(1,0,0,0,0,1,0) + D7(1,0,0,0,0,0,1) + D7(2,0,0,0,0,0,0)
sage: E8(0,0,0,0,0,0,0,1).branch(D7,rule="levi") # long time (3s)
 D7(0,0,0,0,0,0,0) + D7(0,0,0,0,0,1,0) + D7(0,0,0,0,0,0,1) + 2*D7(1,0,0,0,0,0,0) + D7(0,1,0,0,0,0,0)
sage: [F4(fw).branch(B3,rule="levi") for fw in F4.fundamental_weights()] # long time (36s)
 [B3(0,0,0) + 2*B3(1/2,1/2,1/2) + 2*B3(1,0,0) + B3(1,1,0),
 B3(0,0,0) + 6*B3(1/2,1/2,1/2) + 5*B3(1,0,0) + 7*B3(1,1,0) + 3*B3(1,1,1)
 + 6*B3(3/2,1/2,1/2) + 2*B3(3/2,3/2,1/2) + B3(2,0,0) + 2*B3(2,1,0) + B3(2,1,1),
 3*B3(0,0,0) + 6*B3(1/2,1/2,1/2) + 4*B3(1,0,0) + 3*B3(1,1,0) + B3(1,1,1) + 2*B3(3/2,1/2,1/2),
 3*B3(0,0,0) + 2*B3(1/2,1/2,1/2) + B3(1,0,0)]
sage: [F4(fw).branch(C3,rule="levi") for fw in F4.fundamental_weights()] # long time (6s)
 [3*C3(0,0,0) + 2*C3(1,1,1) + C3(2,0,0),
 3*C3(0,0,0) + 6*C3(1,1,1) + 4*C3(2,0,0) + 2*C3(2,1,0) + 3*C3(2,2,0) + C3(2,2,2) + C3(3,1,0) + 2*C3(3,1,1),
 2*C3(1,0,0) + 3*C3(1,1,0) + C3(2,0,0) + 2*C3(2,1,0) + C3(2,1,1),
 2*C3(1,0,0) + C3(1,1,0)]
sage: A1xA1 = WeylCharacterRing("A1xA1")
sage: [A3(hwv).branch(A1xA1,rule="levi") for hwv in A3.fundamental_weights()]
[A1xA1(0,0,1,0) + A1xA1(1,0,0,0),
 A1xA1(0,0,1,1) + A1xA1(1,0,1,0) + A1xA1(1,1,0,0),
 A1xA1(1,0,1,1) + A1xA1(1,1,1,0)]
sage: A1xB1=WeylCharacterRing("A1xB1",style="coroots")
sage: [B3(x).branch(A1xB1,rule="levi") for x in B3.fundamental_weights()]
[A1xB1(0,2) + 2*A1xB1(1,0),
 3*A1xB1(0,0) + A1xB1(0,2) + 2*A1xB1(1,2) + A1xB1(2,0),
 2*A1xB1(0,1) + A1xB1(1,1)]

EXAMPLES: (Automorphic type, including D4 triality)

sage: [A3(chi).branch(A3,rule="automorphic") for chi in A3.fundamental_weights()]
[A3(0,0,0,-1), A3(0,0,-1,-1), A3(0,-1,-1,-1)]
sage: [D4(chi).branch(D4,rule="automorphic") for chi in D4.fundamental_weights()]
[D4(1,0,0,0), D4(1,1,0,0), D4(1/2,1/2,1/2,1/2), D4(1/2,1/2,1/2,-1/2)]
sage: [D4(chi).branch(D4,rule="triality") for chi in D4.fundamental_weights()]
[D4(1/2,1/2,1/2,-1/2), D4(1,1,0,0), D4(1/2,1/2,1/2,1/2), D4(1,0,0,0)]

EXAMPLES: (Symmetric type)

sage: [w.branch(B2,rule="symmetric") for w in [A4(1,0,0,0,0),A4(1,1,0,0,0),A4(1,1,1,0,0),A4(2,0,0,0,0)]]
[B2(1,0), B2(1,1), B2(1,1), B2(0,0) + B2(2,0)]
sage: [A5(w).branch(C3,rule="symmetric") for w in A5.fundamental_weights()]
[C3(1,0,0), C3(0,0,0) + C3(1,1,0), C3(1,0,0) + C3(1,1,1), C3(0,0,0) + C3(1,1,0), C3(1,0,0)]
sage: [A5(w).branch(D3,rule="symmetric") for w in A5.fundamental_weights()]
[D3(1,0,0), D3(1,1,0), D3(1,1,-1) + D3(1,1,1), D3(1,1,0), D3(1,0,0)]
sage: [D4(x).branch(B3,rule="symmetric") for x in D4.fundamental_weights()]
[B3(0,0,0) + B3(1,0,0), B3(1,0,0) + B3(1,1,0), B3(1/2,1/2,1/2), B3(1/2,1/2,1/2)]
sage: [D4(x).branch(G2,rule="symmetric") for x in D4.fundamental_weights()]
[G2(0,0,0) + G2(1,0,-1), 2*G2(1,0,-1) + G2(2,-1,-1), G2(0,0,0) + G2(1,0,-1), G2(0,0,0) + G2(1,0,-1)]
sage: [E6(fw).branch(F4,rule="symmetric") for fw in E6.fundamental_weights()] # long time (36s)
[F4(0,0,0,0) + F4(0,0,0,1),
 F4(0,0,0,1) + F4(1,0,0,0),
 F4(0,0,0,1) + F4(1,0,0,0) + F4(0,0,1,0),
 F4(1,0,0,0) + 2*F4(0,0,1,0) + F4(1,0,0,1) + F4(0,1,0,0),
 F4(0,0,0,1) + F4(1,0,0,0) + F4(0,0,1,0),
 F4(0,0,0,0) + F4(0,0,0,1)]

EXAMPLES: (Extended type)

sage: [B3(x).branch(D3,rule="extended") for x in B3.fundamental_weights()]
[D3(0,0,0) + D3(1,0,0),
 D3(1,0,0) + D3(1,1,0),
 D3(1/2,1/2,-1/2) + D3(1/2,1/2,1/2)]
sage: [G2(w).branch(A2, rule="extended") for w in G2.fundamental_weights()]
[A2(0,0,0) + A2(1/3,1/3,-2/3) + A2(2/3,-1/3,-1/3),
 A2(1/3,1/3,-2/3) + A2(2/3,-1/3,-1/3) + A2(1,0,-1)]
sage: [F4(fw).branch(B4,rule="extended") for fw in F4.fundamental_weights()] # long time (9s)
[B4(1/2,1/2,1/2,1/2) + B4(1,1,0,0),
 B4(1,1,0,0) + B4(1,1,1,0) + B4(3/2,1/2,1/2,1/2) + B4(3/2,3/2,1/2,1/2) + B4(2,1,1,0),
 B4(1/2,1/2,1/2,1/2) + B4(1,0,0,0) + B4(1,1,0,0) + B4(1,1,1,0) + B4(3/2,1/2,1/2,1/2),
 B4(0,0,0,0) + B4(1/2,1/2,1/2,1/2) + B4(1,0,0,0)]

sage: E6 = WeylCharacterRing("E6", style="coroots")
sage: A2xA2xA2=WeylCharacterRing("A2xA2xA2",style="coroots")
sage: A5xA1=WeylCharacterRing("A5xA1",style="coroots")
sage: G2 = WeylCharacterRing("G2", style="coroots")
sage: A1xA1 = WeylCharacterRing("A1xA1", style="coroots")
sage: F4 = WeylCharacterRing("F4",style="coroots")
sage: A3xA1 = WeylCharacterRing("A3xA1", style="coroots")
sage: A2xA2 = WeylCharacterRing("A2xA2", style="coroots")
sage: A1xC3 = WeylCharacterRing("A1xC3",style="coroots")

sage: E6(1,0,0,0,0,0).branch(A5xA1,rule="extended") # (0.7s)
 A5xA1(0,0,0,1,0,0) + A5xA1(1,0,0,0,0,1)
sage: E6(1,0,0,0,0,0).branch(A2xA2xA2, rule="extended") # (0.7s)
 A2xA2xA2(0,0,0,1,1,0) + A2xA2xA2(0,1,1,0,0,0) + A2xA2xA2(1,0,0,0,0,1)
sage: E7=WeylCharacterRing("E7",style="coroots")
sage: A7=WeylCharacterRing("A7",style="coroots")
sage: E7(1,0,0,0,0,0,0).branch(A7,rule="extended") # long time (5s)
 A7(0,0,0,1,0,0,0) + A7(1,0,0,0,0,0,1)
sage: E8=WeylCharacterRing("E8",cache=true,style="coroots")
sage: D8=WeylCharacterRing("D8",cache=true,style="coroots")
sage: E8(0,0,0,0,0,0,0,1).branch(D8,rule="extended") # long time (19s)
 D8(0,0,0,0,0,0,1,0) + D8(0,1,0,0,0,0,0,0)
sage: F4(1,0,0,0).branch(A1xC3,rule="extended") # (0.7s)
 A1xC3(0,2,0,0) + A1xC3(1,0,0,1) + A1xC3(2,0,0,0)
sage: G2(0,1).branch(A1xA1, rule="extended")
 A1xA1(0,2) + A1xA1(2,0) + A1xA1(3,1)
sage: F4(0,0,0,1).branch(A2xA2, rule="extended") # (0.4s)
 A2xA2(0,0,1,1) + A2xA2(0,1,0,1) + A2xA2(1,0,1,0)
sage: F4(0,0,0,1).branch(A3xA1,rule="extended") # (0.34s)
 A3xA1(0,0,0,0) + A3xA1(0,0,0,2) + A3xA1(0,0,1,1) + A3xA1(0,1,0,0) + A3xA1(1,0,0,1)
sage: D4=WeylCharacterRing("D4",style="coroots")
sage: D2xD2=WeylCharacterRing("D2xD2",style="coroots") # We get D4 => A1xA1xA1xA1 by remembering that A1xA1 = D2.
sage: [D4(fw).branch(D2xD2, rule="extended") for fw in D4.fundamental_weights()]
[D2xD2(0,0,1,1) + D2xD2(1,1,0,0),
 D2xD2(0,0,2,0) + D2xD2(0,0,0,2) + D2xD2(2,0,0,0) + D2xD2(1,1,1,1) + D2xD2(0,2,0,0),
 D2xD2(1,0,0,1) + D2xD2(0,1,1,0),
 D2xD2(1,0,1,0) + D2xD2(0,1,0,1)]

EXAMPLES: (Tensor type)

sage: A5=WeylCharacterRing("A5", style="coroots")
sage: A2xA1=WeylCharacterRing("A2xA1", style="coroots")
sage: [A5(hwv).branch(A2xA1, rule="tensor") for hwv in A5.fundamental_weights()]
[A2xA1(1,0,1),
 A2xA1(0,1,2) + A2xA1(2,0,0),
 A2xA1(0,0,3) + A2xA1(1,1,1),
 A2xA1(1,0,2) + A2xA1(0,2,0),
 A2xA1(0,1,1)]

sage: B4=WeylCharacterRing("B4",style="coroots")
sage: B1xB1=WeylCharacterRing("B1xB1",style="coroots")
sage: [B4(f).branch(B1xB1,rule="tensor") for f in B4.fundamental_weights()]
[B1xB1(2,2),
 B1xB1(0,2) + B1xB1(2,0) + B1xB1(2,4) + B1xB1(4,2),
 B1xB1(0,2) + B1xB1(0,6) + B1xB1(2,0) + B1xB1(2,2) + B1xB1(2,4) + B1xB1(4,2) + B1xB1(4,4) + B1xB1(6,0),
 B1xB1(1,3) + B1xB1(3,1)]

sage: D4=WeylCharacterRing("D4",style="coroots")
sage: C2xC1=WeylCharacterRing("C2xC1",style="coroots")
sage: [D4(f).branch(C2xC1,rule="tensor") for f in D4.fundamental_weights()]
[C2xC1(1,0,1),
 C2xC1(0,0,2) + C2xC1(0,1,2) + C2xC1(2,0,0),
 C2xC1(1,0,1),
 C2xC1(0,0,2) + C2xC1(0,1,0)]

sage: C3=WeylCharacterRing("C3",style="coroots")
sage: B1xC1=WeylCharacterRing("B1xC1",style="coroots")
sage: [C3(f).branch(B1xC1,rule="tensor") for f in C3.fundamental_weights()]
[B1xC1(2,1), B1xC1(2,2) + B1xC1(4,0), B1xC1(0,3) + B1xC1(4,1)]

EXAMPLES: (Symmetric Power)

sage: A1=WeylCharacterRing("A1",style="coroots")
sage: B3=WeylCharacterRing("B3",style="coroots")
sage: C3=WeylCharacterRing("C3",style="coroots")
sage: [B3(fw).branch(A1,rule="symmetric_power") for fw in B3.fundamental_weights()]
[A1(6), A1(2) + A1(6) + A1(10), A1(0) + A1(6)]
sage: [C3(fw).branch(A1,rule="symmetric_power") for fw in C3.fundamental_weights()]
[A1(5), A1(4) + A1(8), A1(3) + A1(9)]

EXAMPLES: (Miscellaneous type)

sage: G2 = WeylCharacterRing("G2")
sage: [fw1, fw2, fw3] = B3.fundamental_weights()
sage: B3(fw1+fw3).branch(G2, rule="miscellaneous")
G2(1,0,-1) + G2(2,-1,-1) + G2(2,0,-2)

EXAMPLES: (Isomorphic type)

sage: [B2(x).branch(C2, rule="isomorphic") for x in B2.fundamental_weights()]
[C2(1,1), C2(1,0)]
sage: [C2(x).branch(B2, rule="isomorphic") for x in C2.fundamental_weights()]
[B2(1/2,1/2), B2(1,0)]
sage: [A3(x).branch(D3,rule="isomorphic") for x in A3.fundamental_weights()]
[D3(1/2,1/2,1/2), D3(1,0,0), D3(1/2,1/2,-1/2)]
sage: [D3(x).branch(A3,rule="isomorphic") for x in D3.fundamental_weights()]
[A3(1/2,1/2,-1/2,-1/2), A3(1/4,1/4,1/4,-3/4), A3(3/4,-1/4,-1/4,-1/4)]

Here A3(x,y,z,w) can be understood as a representation of SL(4). The weights x,y,z,w and x+t,y+t,z+t,w+t represent the same representation of SL(4) - though not of GL(4) - since A3(x+t,y+t,z+t,w+t) is the same as A3(x,y,z,w) tensored with 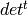$det^t$ . So as a representation of SL(4), A3(1/4,1/4,1/4,-3/4) is the same as A3(1,1,1,0). The exterior square representation SL(4) -> GL(6) admits an invariant symmetric bilinear form, so is a representation SL(4) -> SO(6) that lifts to an isomorphism SL(4) -> Spin(6). Conversely, there are two isomorphisms SO(6) -> SL(4), of which we’ve selected one.

In cases like this you might prefer style=”coroots”.

sage: A3 = WeylCharacterRing("A3",style="coroots")
sage: D3 = WeylCharacterRing("D3",style="coroots")
sage: [D3(fw) for fw in D3.fundamental_weights()]
[D3(1,0,0), D3(0,1,0), D3(0,0,1)]
sage: [D3(fw).branch(A3,rule="isomorphic") for fw in D3.fundamental_weights()]
[A3(0,1,0), A3(0,0,1), A3(1,0,0)]
sage: D2 = WeylCharacterRing("D2", style="coroots")
sage: A1xA1 = WeylCharacterRing("A1xA1", style="coroots")
sage: [D2(fw).branch(A1xA1,rule="isomorphic") for fw in D2.fundamental_weights()]
[A1xA1(1,0), A1xA1(0,1)]

EXAMPLES: (Branching rules from plethysms)

This is a general rule that includes any branching rule from types A,B,C or D as a special case. Thus it could be used in place of the above rules and would give the same results. However it is most useful when branching from G to a maximal subgroup H such that rank(H) < rank(G)-1.

We consider a homomorphism H –> G where G is one of SL(r+1), SO(2r+1), Sp(2r) or SO(2r). The function branching_rule_from_plethysm produces the corresponding branching rule. The main ingredient is the character chi of the representation of H that is the homomorphism to GL(r+1), GL(2r+1) or GL(2r).

This rule is so powerful that it contains the other rules implemented above as special cases. First let us consider the symmetric fifth power representation of SL(2).

sage: A1=WeylCharacterRing("A1",style="coroots")
sage: chi=A1([5])
sage: chi.degree()
 6
sage: chi.frobenius_schur_indicator()
-1

This confirms that the character has degree 6 and is symplectic, so it corresponds to a homomorphism SL(2) –> Sp(6), and there is a corresponding branching rule C3 => A1.

sage: C3 = WeylCharacterRing("C3",style="coroots")
sage: sym5rule = branching_rule_from_plethysm(chi,"C3")
sage: [C3(hwv).branch(A1,rule=sym5rule) for hwv in C3.fundamental_weights()]
[A1(5), A1(4) + A1(8), A1(3) + A1(9)]

This is identical to the results we would obtain using rule=”symmetric_power”. The next example gives a branching not available by other standard rules.

sage: G2 = WeylCharacterRing("G2",style="coroots")
sage: D7 = WeylCharacterRing("D7",style="coroots")
sage: ad=G2(0,1); ad.degree(); ad.frobenius_schur_indicator()
 14
 1
sage: spin = D7(0,0,0,0,0,1,0); spin.degree()
 64
sage: spin.branch(G2, rule=branching_rule_from_plethysm(ad, "D7"))
 G2(1,1)

We have confirmed that the adjoint representation of G2 gives a homomorphism into SO(14), and that the pullback of the one of the two 64 dimensional spin representations to SO(14) is an irreducible representation of G2.

BRANCHING FROM A REDUCIBLE ROOT SYSTEM

If you are branching from a reducible root system, the rule is a list of rules, one for each component type in the root system. The rules in the list are given in pairs [type, rule], where type is the root system to be branched to, and rule is the branching rule.

sage: D4 = WeylCharacterRing("D4",style="coroots")
sage: D2xD2 = WeylCharacterRing("D2xD2",style="coroots")
sage: A1xA1xA1xA1 = WeylCharacterRing("A1xA1xA1xA1",style="coroots")
sage: rr = [["A1xA1","isomorphic"],["A1xA1","isomorphic"]]
sage: [D4(fw) for fw in D4.fundamental_weights()]
[D4(1,0,0,0), D4(0,1,0,0), D4(0,0,1,0), D4(0,0,0,1)]
sage: [D4(fw).branch(D2xD2,rule="extended").branch(A1xA1xA1xA1,rule=rr) for fw in D4.fundamental_weights()]
[A1xA1xA1xA1(0,0,1,1) + A1xA1xA1xA1(1,1,0,0),
 A1xA1xA1xA1(0,0,0,2) + A1xA1xA1xA1(0,0,2,0) + A1xA1xA1xA1(0,2,0,0) + A1xA1xA1xA1(1,1,1,1) + A1xA1xA1xA1(2,0,0,0),
 A1xA1xA1xA1(0,1,1,0) + A1xA1xA1xA1(1,0,0,1),
 A1xA1xA1xA1(0,1,0,1) + A1xA1xA1xA1(1,0,1,0)]

WRITING YOUR OWN RULES

Suppose you want to branch from a group G to a subgroup H. Arrange the embedding so that a Cartan subalgebra U of H is contained in a Cartan subalgebra T of G. There is thus a mapping from the weight spaces Lie(T)* –> Lie(U)*. Two embeddings will produce identical branching rules if they differ by an element of the Weyl group of H.

The RULE is this map Lie(T)* = G.space() to Lie(U)* = H.space(), which you may implement as a function. As an example, let us consider how to implement the branching rule A3 => C2. Here H = C2 = Sp(4) embedded as a subgroup in A3 = GL(4). The Cartan subalgebra U consists of diagonal matrices with eigenvalues u1, u2, -u2, -u1. The C2.space() is the two dimensional vector spaces consisting of the linear functionals u1 and u2 on U. On the other hand Lie(T) is RR^4. A convenient way to see the restriction is to think of it as the adjoint of the map [u1,u2] -> [u1,u2,-u2,-u1], that is, [x0,x1,x2,x3] -> [x0-x3,x1-x2]. Hence we may encode the rule:

def rule(x):
    return [x[0]-x[3],x[1]-x[2]]

or simply:

rule = lambda x : [x[0]-x[3],x[1]-x[2]]

EXAMPLES:

sage: A3 = WeylCharacterRing(['A',3])
sage: C2 = WeylCharacterRing(['C',2])
sage: rule = lambda x : [x[0]-x[3],x[1]-x[2]]
sage: branch_weyl_character(A3([1,1,0,0]),A3,C2,rule)
C2(0,0) + C2(1,1)
sage: A3(1,1,0,0).branch(C2, rule) == C2(0,0) + C2(1,1)
True

sage.combinat.root_system.weyl_characters.branching_rule_from_plethysm(chi, cartan_type, return_matrix=False)¶

INPUT:

chi - the character of an irreducible representation pi of a group G
cartan_type - a classical Cartan type (A,B,C or D).

It is assumed that the image of the irreducible representation pi naturally has its image in the group G.

Returns a branching rule for this plethysm.

EXAMPLE:

The adjoint representation SL(3) –> GL(8) factors through SO(8). The branching rule in question will describe how representations of SO(8) composed with this homomorphism decompose into irreducible characters of SL(3):

sage: A2 = WeylCharacterRing("A2")
sage: A2 = WeylCharacterRing("A2", style="coroots")
sage: ad = A2(1,1)
sage: ad.degree()
8
sage: ad.frobenius_schur_indicator()
1

This confirms that 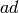$ad$ has degree 8 and is orthogonal, hence factors through SO(8)=D4:

sage: br = branching_rule_from_plethysm(ad,"D4")
sage: D4 = WeylCharacterRing("D4")
sage: [D4(f).branch(A2,rule = br) for f in D4.fundamental_weights()]
[A2(1,1), A2(1,1) + A2(0,3) + A2(3,0), A2(1,1), A2(1,1)]

sage.combinat.root_system.weyl_characters.get_branching_rule(Rtype, Stype, rule)¶

INPUT:

R - the Weyl Character Ring of G
S - the Weyl Character Ring of H
rule - a string describing the branching rule as a map from the weight space of S to the weight space of R.

sage.combinat.root_system.weyl_characters.irreducible_character_freudenthal(hwv, L, debug=False)¶

Returns the dictionary of multiplicities for the irreducible character with highest weight lamb. The weight multiplicities are computed by the Freudenthal multiplicity formula. The algorithm is based on recursion relation that is stated, for example, in Humphrey’s book on Lie Algebras. The multiplicities are invariant under the Weyl group, so to compute them it would be sufficient to compute them for the weights in the positive Weyl chamber. However after some testing it was found to be faster to compute every weight using the recursion, since the use of the Weyl group is expensive in its current implementation.

INPUT:

hwv - a dominant weight in a weight lattice.
L - the ambient space

Weyl Characters¶

Previous topic

Next topic

This Page

Navigation

Weyl Characters¶

Previous topic

Next topic

This Page

Quick search

Navigation