Root systems¶

Quickref¶

T = CartanType([“A”, 3]), T.is_finite() Cartan types

T.dynkin_diagram(), DynkinDiagram([“G”,2]) Dynkin diagrams

T.cartan_matrix(), CartanMatrix([“F”,4]) Cartan matrices

RootSystem(T).weight_lattice() Root systems

WeylGroup([“B”, 6, 1]).simple_reflections() Affine weyl groups

WeylCharacterRing([“D”, 4]) Weyl character rings

Documentation¶

sage.combinat.root_system This current overview

CartanType An introduction to Cartan types

RootSystem An introduction to root systems

See also¶

CoxeterGroups, WeylGroups, ... The categories of Coxeter and Weyl groups
sage.combinat.crystals An introduction to crystals
type_A, type_B_affine, ... Type specific root system data

class sage.combinat.root_system.root_system.RootSystem(cartan_type, as_dual_of=None)¶

Bases: sage.structure.unique_representation.UniqueRepresentation, sage.structure.sage_object.SageObject

A class for root systems.

EXAMPLES:

We construct the root system for type $B_3$ :

sage: R=RootSystem(['B',3]); R
Root system of type ['B', 3]

R models the root system abstractly. It comes equipped with various realizations of the root and weight lattices, where all computation take place. Let us play first with the root lattice:

sage: space = R.root_lattice()
sage: space
Root lattice of the Root system of type ['B', 3]

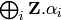It is the free $\ZZ$ -module $\bigoplus_i \ZZ.\alpha_i$ spanned by the simple roots:

sage: space.base_ring()
Integer Ring
sage: list(space.basis()) 
[alpha[1], alpha[2], alpha[3]]

Let us do some computations with the simple roots:

sage: alpha = space.simple_roots()
sage: alpha[1] + alpha[2]
alpha[1] + alpha[2]

There is a canonical pairing between the root lattice and the coroot lattice:

sage: R.coroot_lattice()
Coroot lattice of the Root system of type ['B', 3]

We construct the simple coroots, and do some computations (see comments about duality below for some caveat):

sage: alphacheck = space.simple_coroots()
sage: list(alphacheck)
[alphacheck[1], alphacheck[2], alphacheck[3]]

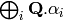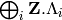We can carry over the same computations in any of the other realizations of the root lattice, like the root space $\bigoplus_i \QQ.\alpha_i$ , the weight lattice $\bigoplus_i \ZZ.\Lambda_i$ , the weight space $\bigoplus_i \QQ.\Lambda_i$ . For example:

sage: space = R.weight_space()
sage: space
Weight space over the Rational Field of the Root system of type ['B', 3]

sage: space.base_ring()
Rational Field
sage: list(space.basis())
[Lambda[1], Lambda[2], Lambda[3]]

sage: alpha = space.simple_roots()
sage: alpha[1] + alpha[2]
Lambda[1] + Lambda[2] - 2*Lambda[3]

The fundamental weights are the dual basis of the coroots:

sage: Lambda = space.fundamental_weights()
sage: Lambda[1]
Lambda[1]

sage: alphacheck = space.simple_coroots()
sage: list(alphacheck)
[alphacheck[1], alphacheck[2], alphacheck[3]]

sage: [Lambda[i].scalar(alphacheck[1]) for i in space.index_set()]
[1, 0, 0]
sage: [Lambda[i].scalar(alphacheck[2]) for i in space.index_set()]
[0, 1, 0]
sage: [Lambda[i].scalar(alphacheck[3]) for i in space.index_set()]
[0, 0, 1]

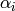Let us use the simple reflections. In the weight space, they work as in the number game: firing the node $i$ on an element $x$ adds $c$ times the simple root $\alpha_i$ , where $c$ is the coefficient of $i$ in $x$ :

sage: s = space.simple_reflections()
sage: Lambda[1].simple_reflection(1)
-Lambda[1] + Lambda[2]
sage: Lambda[2].simple_reflection(1)
Lambda[2]
sage: Lambda[3].simple_reflection(1)
Lambda[3]
sage: (-2*Lambda[1] + Lambda[2] + Lambda[3]).simple_reflection(1)
2*Lambda[1] - Lambda[2] + Lambda[3]

It can be convenient to manipulate the simple reflections themselves:

sage: s = space.simple_reflections()
sage: s[1](Lambda[1])
-Lambda[1] + Lambda[2]
sage: s[1](Lambda[2])
Lambda[2]
sage: s[1](Lambda[3])
Lambda[3]

The root system may also come equipped with an ambient space, that is a simultaneous realization of the weight lattice and the coroot lattice in a Euclidean vector space. This is implemented on a type by type basis, and is not always available. When the coefficients permit it, this is also available as an ambient lattice.

TODO: Demo: signed permutations realization of type B

The root system is aware of its dual root system:

sage: R.dual
Dual of root system of type ['B', 3]

R.dual is really the root system of type 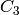$C_3$ :

sage: R.dual.cartan_type()
['C', 3]

And the coroot lattice that we have been manipulating before is really implemented as the root lattice of the dual root system:

sage: R.dual.root_lattice()
Coroot lattice of the Root system of type ['B', 3]

In particular, the coroots for the root lattice are in fact the roots of the coroot lattice:

sage: list(R.root_lattice().simple_coroots())
[alphacheck[1], alphacheck[2], alphacheck[3]]
sage: list(R.coroot_lattice().simple_roots())
[alphacheck[1], alphacheck[2], alphacheck[3]]
sage: list(R.dual.root_lattice().simple_roots())
[alphacheck[1], alphacheck[2], alphacheck[3]]

The coweight lattice and space are defined similarly. Note that, to limit confusion, all the output have been tweaked appropriately.

TESTS:

sage: R = RootSystem(['C',3])
sage: R == loads(dumps(R))
True
sage: L = R.ambient_space()
sage: s = L.simple_reflections()
sage: s = L.simple_projections() # todo: not implemented
sage: L == loads(dumps(L))
True
sage: L = R.root_space()
sage: s = L.simple_reflections()
sage: L == loads(dumps(L))
True

sage: for T in CartanType.samples(finite=True,crystalographic=True):
...       TestSuite(RootSystem(T)).run()

ambient_lattice()¶

Returns the usual ambient lattice for this root_system, if it exists and is implemented, and None otherwise. This is a $\ZZ$ -module, endowed with its canonical euclidean scalar product, which embeds simultaneously the root lattice and the coroot lattice (what about the weight lattice?)

EXAMPLES:

sage: RootSystem(['A',4]).ambient_lattice()
Ambient lattice of the Root system of type ['A', 4]

sage: RootSystem(['B',4]).ambient_lattice()
sage: RootSystem(['C',4]).ambient_lattice()
sage: RootSystem(['D',4]).ambient_lattice()
sage: RootSystem(['E',6]).ambient_lattice()
sage: RootSystem(['F',4]).ambient_lattice()
sage: RootSystem(['G',2]).ambient_lattice()

ambient_space(*args, **kwds)¶

Returns the usual ambient space for this root_system, if it is implemented, and None otherwise. This is a $\QQ$ -module, endowed with its canonical euclidean scalar product, which embeds simultaneously the root lattice and the coroot lattice (what about the weight lattice?). An alternative base ring can be provided as an option; it must contain the smallest ring over which the ambient space can be defined ( $\ZZ$ or $\QQ$ , depending on the type).

EXAMPLES:

sage: RootSystem(['A',4]).ambient_space()
Ambient space of the Root system of type ['A', 4]

sage: RootSystem(['B',4]).ambient_space()
Ambient space of the Root system of type ['B', 4]

sage: RootSystem(['C',4]).ambient_space()
Ambient space of the Root system of type ['C', 4]

sage: RootSystem(['D',4]).ambient_space()
Ambient space of the Root system of type ['D', 4]

sage: RootSystem(['E',6]).ambient_space()
Ambient space of the Root system of type ['E', 6]

sage: RootSystem(['F',4]).ambient_space()
Ambient space of the Root system of type ['F', 4]

sage: RootSystem(['G',2]).ambient_space()
Ambient space of the Root system of type ['G', 2]

cartan_matrix(*args, **kwds)¶

EXAMPLES:

sage: RootSystem(['A',3]).cartan_matrix()
[ 2 -1  0]
[-1  2 -1]
[ 0 -1  2]

cartan_type()¶

Returns the Cartan type of the root system.

EXAMPLES:

sage: R = RootSystem(['A',3])
sage: R.cartan_type()
['A', 3]

coroot_lattice()¶

Returns the coroot lattice associated to self.

EXAMPLES:

sage: RootSystem(['A',3]).coroot_lattice()
Coroot lattice of the Root system of type ['A', 3]

coroot_space(base_ring=Rational Field)¶

Returns the coroot space associated to self.

EXAMPLES:

sage: RootSystem(['A',3]).coroot_space()
Coroot space over the Rational Field of the Root system of type ['A', 3]

coweight_lattice()¶

Returns the coweight lattice associated to self.

EXAMPLES:

sage: RootSystem(['A',3]).coweight_lattice()
Coweight lattice of the Root system of type ['A', 3]

coweight_space(base_ring=Rational Field)¶

Returns the weight space associated to self.

EXAMPLES:

sage: RootSystem(['A',3]).coweight_space()
Coweight space over the Rational Field of the Root system of type ['A', 3]

dynkin_diagram(*args, **kwds)¶

Returns the Dynkin diagram of the root system.

EXAMPLES:

sage: R = RootSystem(['A',3])
sage: R.dynkin_diagram()
O---O---O
1   2   3
A3

index_set()¶

EXAMPLES:

sage: RootSystem(['A',3]).index_set()
[1, 2, 3]

is_finite(*args, **kwds)¶

Returns True if self is a finite root system.

EXAMPLES:

sage: RootSystem(["A",3]).is_finite()
True
sage: RootSystem(["A",3,1]).is_finite()
False

is_irreducible(*args, **kwds)¶

Returns True if self is an irreducible root system.

EXAMPLES:

sage: RootSystem(['A', 3]).is_irreducible()
True
sage: RootSystem("A2xB2").is_irreducible()
False

root_lattice()¶

Returns the root lattice associated to self.

EXAMPLES:

sage: RootSystem(['A',3]).root_lattice()
Root lattice of the Root system of type ['A', 3]

root_space(*args, **kwds)¶

Returns the root space associated to self.

EXAMPLES

sage: RootSystem(['A',3]).root_space()
Root space over the Rational Field of the Root system of type ['A', 3]

weight_lattice()¶

Returns the weight lattice associated to self.

EXAMPLES:

sage: RootSystem(['A',3]).weight_lattice()
Weight lattice of the Root system of type ['A', 3]

weight_space(*args, **kwds)¶

Returns the weight space associated to self.

EXAMPLES:

sage: RootSystem(['A',3]).weight_space()
Weight space over the Rational Field of the Root system of type ['A', 3]

sage.combinat.root_system.root_system.WeylDim(ct, coeffs)¶

The Weyl Dimension Formula.

INPUT:

type - a Cartan type
coeffs - a list of nonnegative integers

The length of the list must equal the rank type[1]. A dominant weight hwv is constructed by summing the fundamental weights with coefficients from this list. The dimension of the irreducible representation of the semisimple complex Lie algebra with highest weight vector hwv is returned.

EXAMPLES:

For $SO(7)$ , the Cartan type is $B_3$ , so:

sage: WeylDim(['B',3],[1,0,0]) # standard representation of SO(7)
7
sage: WeylDim(['B',3],[0,1,0]) # exterior square
21
sage: WeylDim(['B',3],[0,0,1]) # spin representation of spin(7)
8
sage: WeylDim(['B',3],[1,0,1]) # sum of the first and third fundamental weights
48
sage: [WeylDim(['F',4],x) for x in [1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]]
[52, 1274, 273, 26]
sage: [WeylDim(['E', 6], x) for x in [0, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0], [0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 2], [0, 0, 0, 0, 1, 0], [0, 0, 1, 0, 0, 0], [1, 0, 0, 0, 0, 0], [1, 0, 0, 0, 0, 1], [2, 0, 0, 0, 0, 0]]
[1, 78, 27, 351, 351, 351, 27, 650, 351]

Root systems¶

Quickref¶

Documentation¶

See also¶

Table Of Contents

Previous topic

Next topic

This Page

Navigation

Root systems¶

Quickref¶

Documentation¶

See also¶

Table Of Contents

Previous topic

Next topic

This Page

Quick search

Navigation