Matrix Group Elements

AUTHORS:

• David Joyner (2006-05): initial version David Joyner
• David Joyner (2006-05): various modifications to address William Stein’s TODO’s.
• William Stein (2006-12-09): many revisions.

EXAMPLES:

sage: F = GF(3); MS = MatrixSpace(F,2,2)
sage: gens = [MS([[1,0],[0,1]]),MS([[1,1],[0,1]])]
sage: G = MatrixGroup(gens); G
Matrix group over Finite Field of size 3 with 2 generators: 
 [[[1, 0], [0, 1]], [[1, 1], [0, 1]]]    
sage: g = G([[1,1],[0,1]])
sage: h = G([[1,2],[0,1]])
sage: g*h
[1 0]
[0 1]    

You cannot add two matrices, since this is not a group operation. You can coerce matrices back to the matrix space and add them there:

sage: g + h
...
TypeError: unsupported operand type(s) for +: 'MatrixGroup_gens_finite_field_with_category.element_class' and 'MatrixGroup_gens_finite_field_with_category.element_class'

sage: g.matrix() + h.matrix()
[2 0]
[0 2]

sage: 2*g
...
TypeError: unsupported operand parent(s) for '*': 'Integer Ring' and 'Matrix group over Finite Field of size 3 with 2 generators: 
 [[[1, 0], [0, 1]], [[1, 1], [0, 1]]]'
sage: 2*g.matrix()
[2 2]
[0 2]

class sage.groups.matrix_gps.matrix_group_element.MatrixGroupElement(g, parent, check=True)

Bases: sage.structure.element.MultiplicativeGroupElement

An element of a matrix group.

EXAMPLES:

sage: F = GF(3); MS = MatrixSpace(F,2,2)
       sage: gens = [MS([[1,0],[0,1]]),MS([[1,1],[0,1]])]
sage: G = MatrixGroup(gens)
sage: g = G.random_element()
sage: type(g)
<class 'sage.groups.matrix_gps.matrix_group_element.MatrixGroup_gens_finite_field_with_category.element_class'>

list()

Return list representation of this matrix.

EXAMPLES:

sage: F = GF(3); MS = MatrixSpace(F,2,2)
sage: gens = [MS([[1,0],[0,1]]),MS([[1,1],[0,1]])]
sage: G = MatrixGroup(gens)
sage: g = G.0
sage: g.list()   
[[1, 0], [0, 1]]

matrix()

Obtain the usual matrix (as an element of a matrix space) associated to this matrix group element.

One reason to compute the associated matrix is that matrices support a huge range of functionality.

EXAMPLES:

sage: k = GF(7); G = MatrixGroup([matrix(k,2,[1,1,0,1]), matrix(k,2,[1,0,0,2])])
sage: g = G.0
sage: g.matrix()
[1 1]
[0 1]
sage: parent(g.matrix())
Full MatrixSpace of 2 by 2 dense matrices over Finite Field of size 7

Matrices have extra functionality that matrix group elements do not have.

sage: g.matrix().charpoly('t')
t^2 + 5*t + 1

order()

Return the order of this group element, which is the smallest positive integer such that 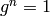, or +Infinity if no such integer exists.

EXAMPLES:

sage: k = GF(7); G = MatrixGroup([matrix(k,2,[1,1,0,1]), matrix(k,2,[1,0,0,2])])
sage: G
Matrix group over Finite Field of size 7 with 2 generators: 
 [[[1, 1], [0, 1]], [[1, 0], [0, 2]]]
sage: G.order()
21        

See trac #1170

sage: gl=GL(2,ZZ); gl  
General Linear Group of degree 2 over Integer Ring
sage: g=gl.gens()[2]; g
[1 1]
[0 1]
sage: g.order()        
+Infinity

word_problem(gens=None)

Write this group element in terms of the elements of the list gens, or the standard generators of the parent of self if gens is None.

INPUT:

• gens - a list of elements that can be coerced into the parent of self, or None.

ALGORITHM: Use GAP, which has optimized algorithms for solving the word problem (the GAP functions EpimorphismFromFreeGroup and PreImagesRepresentative).

EXAMPLE:

sage: G = GL(2,5); G
General Linear Group of degree 2 over Finite Field of size 5
sage: G.gens()
[
[2 0]
[0 1],
[4 1]
[4 0]
]
sage: G(1).word_problem([G.1, G.0])
1

Next we construct a more complicated element of the group from the generators:

sage: s,t = G.0, G.1
sage: a = (s * t * s); b = a.word_problem(); b
([2 0]
[0 1]) *
([4 1]
[4 0]) *
([2 0]
[0 1])
sage: b.prod() == a
True

We solve the word problem using some different generators:

sage: s = G([2,0,0,1]); t = G([1,1,0,1]); u = G([0,-1,1,0])
sage: a.word_problem([s,t,u])
([2 0]
[0 1])^-1 *
([1 1]
[0 1])^-1 *
([0 4]
[1 0]) *
([2 0]
[0 1])^-1

We try some elements that don’t actually generate the group:

sage: a.word_problem([t,u])
...
ValueError: Could not solve word problem

AUTHORS:

• David Joyner and William Stein
• David Loeffler (2010): fixed some bugs

sage.groups.matrix_gps.matrix_group_element.is_MatrixGroupElement(x)