Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Combinatorics »

The Permutations module. Use Permutation? to get information about the Permutation class, and Permutations? to get information about the combinatorial class of permutations.
AUTHORS:
An arrangement of mset is an ordered selection without repetitions and is represented by a list that contains only elements from mset, but maybe in a different order.
Arrangements returns the combinatorial class of arrangements of the multiset mset that contain k elements.
EXAMPLES:
sage: mset = [1,1,2,3,4,4,5]
sage: Arrangements(mset,2).list()
[[1, 1],
[1, 2],
[1, 3],
[1, 4],
[1, 5],
[2, 1],
[2, 3],
[2, 4],
[2, 5],
[3, 1],
[3, 2],
[3, 4],
[3, 5],
[4, 1],
[4, 2],
[4, 3],
[4, 4],
[4, 5],
[5, 1],
[5, 2],
[5, 3],
[5, 4]]
sage: Arrangements(mset,2).cardinality()
22
sage: Arrangements( ["c","a","t"], 2 ).list()
[['c', 'a'], ['c', 't'], ['a', 'c'], ['a', 't'], ['t', 'c'], ['t', 'a']]
sage: Arrangements( ["c","a","t"], 3 ).list()
[['c', 'a', 't'],
['c', 't', 'a'],
['a', 'c', 't'],
['a', 't', 'c'],
['t', 'c', 'a'],
['t', 'a', 'c']]
Returns the combinatorial class of all cyclic permutations of mset in cycle notation. These are the same as necklaces.
EXAMPLES:
sage: CyclicPermutations(range(4)).list()
[[0, 1, 2, 3],
[0, 1, 3, 2],
[0, 2, 1, 3],
[0, 2, 3, 1],
[0, 3, 1, 2],
[0, 3, 2, 1]]
sage: CyclicPermutations([1,1,1]).list()
[[1, 1, 1]]
Returns the combinatorial class of all combinations of cyclic permutations of each cell of the partition. This is the same as a Cartesian product of necklaces.
EXAMPLES:
sage: CyclicPermutationsOfPartition([[1,2,3,4],[5,6,7]]).list()
[[[1, 2, 3, 4], [5, 6, 7]],
[[1, 2, 4, 3], [5, 6, 7]],
[[1, 3, 2, 4], [5, 6, 7]],
[[1, 3, 4, 2], [5, 6, 7]],
[[1, 4, 2, 3], [5, 6, 7]],
[[1, 4, 3, 2], [5, 6, 7]],
[[1, 2, 3, 4], [5, 7, 6]],
[[1, 2, 4, 3], [5, 7, 6]],
[[1, 3, 2, 4], [5, 7, 6]],
[[1, 3, 4, 2], [5, 7, 6]],
[[1, 4, 2, 3], [5, 7, 6]],
[[1, 4, 3, 2], [5, 7, 6]]]
sage: CyclicPermutationsOfPartition([[1,2,3,4],[4,4,4]]).list()
[[[1, 2, 3, 4], [4, 4, 4]],
[[1, 2, 4, 3], [4, 4, 4]],
[[1, 3, 2, 4], [4, 4, 4]],
[[1, 3, 4, 2], [4, 4, 4]],
[[1, 4, 2, 3], [4, 4, 4]],
[[1, 4, 3, 2], [4, 4, 4]]]
sage: CyclicPermutationsOfPartition([[1,2,3],[4,4,4]]).list()
[[[1, 2, 3], [4, 4, 4]], [[1, 3, 2], [4, 4, 4]]]
sage: CyclicPermutationsOfPartition([[1,2,3],[4,4,4]]).list(distinct=True)
[[[1, 2, 3], [4, 4, 4]],
[[1, 3, 2], [4, 4, 4]],
[[1, 2, 3], [4, 4, 4]],
[[1, 3, 2], [4, 4, 4]]]
Bases: sage.combinat.combinat.CombinatorialClass
AUTHORS:
EXAMPLES:
sage: CyclicPermutationsOfPartition([[1,2,3,4],[5,6,7]]).list() # indirect doctest
[[[1, 2, 3, 4], [5, 6, 7]],
[[1, 2, 4, 3], [5, 6, 7]],
[[1, 3, 2, 4], [5, 6, 7]],
[[1, 3, 4, 2], [5, 6, 7]],
[[1, 4, 2, 3], [5, 6, 7]],
[[1, 4, 3, 2], [5, 6, 7]],
[[1, 2, 3, 4], [5, 7, 6]],
[[1, 2, 4, 3], [5, 7, 6]],
[[1, 3, 2, 4], [5, 7, 6]],
[[1, 3, 4, 2], [5, 7, 6]],
[[1, 4, 2, 3], [5, 7, 6]],
[[1, 4, 3, 2], [5, 7, 6]]]
sage: CyclicPermutationsOfPartition([[1,2,3,4],[4,4,4]]).list()
[[[1, 2, 3, 4], [4, 4, 4]],
[[1, 2, 4, 3], [4, 4, 4]],
[[1, 3, 2, 4], [4, 4, 4]],
[[1, 3, 4, 2], [4, 4, 4]],
[[1, 4, 2, 3], [4, 4, 4]],
[[1, 4, 3, 2], [4, 4, 4]]]
sage: CyclicPermutationsOfPartition([[1,2,3],[4,4,4]]).list()
[[[1, 2, 3], [4, 4, 4]], [[1, 3, 2], [4, 4, 4]]]
sage: CyclicPermutationsOfPartition([[1,2,3],[4,4,4]]).list(distinct=True)
[[[1, 2, 3], [4, 4, 4]],
[[1, 3, 2], [4, 4, 4]],
[[1, 2, 3], [4, 4, 4]],
[[1, 3, 2], [4, 4, 4]]]
EXAMPLES:
sage: CyclicPermutationsOfPartition([[1,2,3],[4,4,4]]).list()
[[[1, 2, 3], [4, 4, 4]], [[1, 3, 2], [4, 4, 4]]]
sage: CyclicPermutationsOfPartition([[1,2,3],[4,4,4]]).list(distinct=True)
[[[1, 2, 3], [4, 4, 4]],
[[1, 3, 2], [4, 4, 4]],
[[1, 2, 3], [4, 4, 4]],
[[1, 3, 2], [4, 4, 4]]]
Bases: sage.combinat.combinat.CombinatorialClass
EXAMPLES:
sage: CyclicPermutations(range(4)).list() # indirect doctest
[[0, 1, 2, 3],
[0, 1, 3, 2],
[0, 2, 1, 3],
[0, 2, 3, 1],
[0, 3, 1, 2],
[0, 3, 2, 1]]
sage: CyclicPermutations([1,1,1]).list()
[[1, 1, 1]]
sage: CyclicPermutations([1,1,1]).list(distinct=True)
[[1, 1, 1], [1, 1, 1]]
EXAMPLES:
sage: CyclicPermutations(range(4)).list()
[[0, 1, 2, 3],
[0, 1, 3, 2],
[0, 2, 1, 3],
[0, 2, 3, 1],
[0, 3, 1, 2],
[0, 3, 2, 1]]
Converts l to a permutation.
INPUT:
OUTPUT:
EXAMPLES:
sage: Permutation([2,1])
[2, 1]
sage: Permutation([2, 1, 4, 5, 3])
[2, 1, 4, 5, 3]
sage: Permutation('(1,2)')
[2, 1]
sage: Permutation('(1,2)(3,4,5)')
[2, 1, 4, 5, 3]
sage: Permutation( ((1,2),(3,4,5)) )
[2, 1, 4, 5, 3]
sage: Permutation( [(1,2),(3,4,5)] )
[2, 1, 4, 5, 3]
sage: Permutation( ((1,2)) )
[2, 1]
sage: Permutation( (1,2) )
[2, 1]
sage: Permutation( ((1,2),) )
[2, 1]
sage: p = Permutation((1, 2, 5)); p
[2, 5, 3, 4, 1]
sage: type(p)
<class 'sage.combinat.permutation.Permutation_class'>
Construction from a string in cycle notation
sage: p = Permutation( '(4,5)' ); p
[1, 2, 3, 5, 4]
The length of the permutation is the maximum integer appearing; add a 1-cycle to increase this:
sage: p2 = Permutation( '(4,5)(10)' ); p2
[1, 2, 3, 5, 4, 6, 7, 8, 9, 10]
sage: len(p); len(p2)
5
10
We construct a Permutation from a PermutationGroupElement:
sage: g = PermutationGroupElement([2,1,3])
sage: Permutation(g)
[2, 1, 3]
From a pair of tableaux of the same shape. This uses the inverse of Robinson Schensted algorithm:
sage: p = [[1, 4, 7], [2, 5], [3], [6]]
sage: q = [[1, 2, 5], [3, 6], [4], [7]]
sage: P = Tableau(p)
sage: Q = Tableau(q)
sage: Permutation( (p, q) )
[3, 6, 5, 2, 7, 4, 1]
sage: Permutation( [p, q] )
[3, 6, 5, 2, 7, 4, 1]
sage: Permutation( (P, Q) )
[3, 6, 5, 2, 7, 4, 1]
sage: Permutation( [P, Q] )
[3, 6, 5, 2, 7, 4, 1]
TESTS:
sage: Permutation([()])
[1]
sage: Permutation('()')
[1]
sage: Permutation(())
[1]
From a pair of empty tableaux
sage: Permutation( ([], []) )
[]
sage: Permutation( [[], []] )
[]
Sets the global options for elements of the permutation class. The defaults are for permutations to be displayed in list notation and the multiplication done from left to right (like in GAP).
display: ‘list’ - the permutations are displayed in list notation ‘cycle’ - the permutations are displayed in cycle notation ‘singleton’ - the permutations are displayed in cycle notation with singleton cycles shown as well.
mult: ‘l2r’ - the multiplication of permutations is done like composition of functions from left to right. That is, if we think of the permutations p1 and p2 as functions, then (p1*p2)(x) = p2(p1(x)). This is the default in multiplication in GAP. ‘r2l’ - the multiplication of permutations is done right to left so that (p1*p2)(x) = p1(p2(x))
If no parameters are set, then the function returns a copy of the options dictionary.
Note that these options have no effect on PermutationGroupElements.
EXAMPLES:
sage: p213 = Permutation([2,1,3])
sage: p312 = Permutation([3,1,2])
sage: PermutationOptions(mult='l2r', display='list')
sage: po = PermutationOptions()
sage: po['display']
'list'
sage: p213
[2, 1, 3]
sage: PermutationOptions(display='cycle')
sage: p213
(1,2)
sage: PermutationOptions(display='singleton')
sage: p213
(1,2)(3)
sage: PermutationOptions(display='list')
sage: po['mult']
'l2r'
sage: p213*p312
[1, 3, 2]
sage: PermutationOptions(mult='r2l')
sage: p213*p312
[3, 2, 1]
sage: PermutationOptions(mult='l2r')
Bases: sage.combinat.combinat.CombinatorialObject
Returns the action of the permutation on a list.
EXAMPLES:
sage: p = Permutation([2,1,3])
sage: a = range(3)
sage: p.action(a)
[1, 0, 2]
sage: b = [1,2,3,4]
sage: p.action(b)
...
ValueError: len(a) must equal len(self)
Returns True if the permutation avoid the pattern patt and False otherwise.
EXAMPLES:
sage: Permutation([6,2,5,4,3,1]).avoids([4,2,3,1])
False
sage: Permutation([6,1,2,5,4,3]).avoids([4,2,3,1])
True
sage: Permutation([6,1,2,5,4,3]).avoids([3,4,1,2])
True
Returns the combinatorial class of permutations greater than or equal to p in the Bruhat order.
EXAMPLES:
sage: Permutation([4,1,2,3]).bruhat_greater().list()
[[4, 1, 2, 3],
[4, 1, 3, 2],
[4, 2, 1, 3],
[4, 2, 3, 1],
[4, 3, 1, 2],
[4, 3, 2, 1]]
Returns the list of inversions of p such that the application of this inversion to p decrements its number of inversions.
Equivalently, it returns the list of pairs (i,j), i < j such that p[i] < p[j] and such that there exists no k between i and j satisfying p[i] < p[k].
EXAMPLES:
sage: Permutation([5,2,3,4,1]).bruhat_inversions()
[[0, 1], [0, 2], [0, 3], [1, 4], [2, 4], [3, 4]]
sage: Permutation([6,1,4,5,2,3]).bruhat_inversions()
[[0, 1], [0, 2], [0, 3], [2, 4], [2, 5], [3, 4], [3, 5]]
Returns the iterator for the inversions of p such that the application of this inversion to p decrements its number of inversions.
EXAMPLES:
sage: list(Permutation([5,2,3,4,1]).bruhat_inversions_iterator())
[[0, 1], [0, 2], [0, 3], [1, 4], [2, 4], [3, 4]]
sage: list(Permutation([6,1,4,5,2,3]).bruhat_inversions_iterator())
[[0, 1], [0, 2], [0, 3], [2, 4], [2, 5], [3, 4], [3, 5]]
Returns True if self is less than p2 in the Bruhat order.
EXAMPLES:
sage: Permutation([2,4,3,1]).bruhat_lequal(Permutation([3,4,2,1]))
True
Returns a list of the permutations strictly smaller than p in the Bruhat order such that there is no permutation between one of those and p.
EXAMPLES:
sage: Permutation([6,1,4,5,2,3]).bruhat_pred()
[[1, 6, 4, 5, 2, 3],
[4, 1, 6, 5, 2, 3],
[5, 1, 4, 6, 2, 3],
[6, 1, 2, 5, 4, 3],
[6, 1, 3, 5, 2, 4],
[6, 1, 4, 2, 5, 3],
[6, 1, 4, 3, 2, 5]]
An iterator for the permutations strictly smaller than p in the Bruhat order such that there is no permutation between one of those and p.
EXAMPLES:
sage: [x for x in Permutation([6,1,4,5,2,3]).bruhat_pred_iterator()]
[[1, 6, 4, 5, 2, 3],
[4, 1, 6, 5, 2, 3],
[5, 1, 4, 6, 2, 3],
[6, 1, 2, 5, 4, 3],
[6, 1, 3, 5, 2, 4],
[6, 1, 4, 2, 5, 3],
[6, 1, 4, 3, 2, 5]]
Returns a the combinatorial class of permutations smaller than or equal to p in the Bruhat order.
EXAMPLES:
sage: Permutation([4,1,2,3]).bruhat_smaller().list()
[[1, 2, 3, 4],
[1, 2, 4, 3],
[1, 3, 2, 4],
[1, 4, 2, 3],
[2, 1, 3, 4],
[2, 1, 4, 3],
[3, 1, 2, 4],
[4, 1, 2, 3]]
Returns a list of the permutations strictly greater than p in the Bruhat order such that there is no permutation between one of those and p.
EXAMPLES:
sage: Permutation([6,1,4,5,2,3]).bruhat_succ()
[[6, 4, 1, 5, 2, 3],
[6, 2, 4, 5, 1, 3],
[6, 1, 5, 4, 2, 3],
[6, 1, 4, 5, 3, 2]]
An iterator for the permutations that are strictly greater than p in the Bruhat order such that there is no permutation between one of those and p.
EXAMPLES:
sage: [x for x in Permutation([6,1,4,5,2,3]).bruhat_succ_iterator()]
[[6, 4, 1, 5, 2, 3],
[6, 2, 4, 5, 1, 3],
[6, 1, 5, 4, 2, 3],
[6, 1, 4, 5, 3, 2]]
Returns the complement of the permutation which is obtained by replacing each value x in the list with n - x + 1.
EXAMPLES:
sage: Permutation([1,2,3]).complement()
[3, 2, 1]
sage: Permutation([1, 3, 2]).complement()
[3, 1, 2]
Returns a string of the permutation in cycle notation.
If singletons=True, it includes 1-cycles in the string.
EXAMPLES:
sage: Permutation([1,2,3]).cycle_string()
'()'
sage: Permutation([2,1,3]).cycle_string()
'(1,2)'
sage: Permutation([2,3,1]).cycle_string()
'(1,2,3)'
sage: Permutation([2,1,3]).cycle_string(singletons=True)
'(1,2)(3)'
Returns a partition of len(p) corresponding to the cycle type of p. This is a non-increasing sequence of the cycle lengths of p.
EXAMPLES:
sage: Permutation([3,1,2,4]).cycle_type()
[3, 1]
Returns the descent polynomial of the permutation p.
The descent polynomial of p is the product of all the z[p[i]] where i ranges over the descents of p.
REFERENCES:
EXAMPLES:
sage: Permutation([2,1,3]).descent_polynomial()
z1
sage: Permutation([4,3,2,1]).descent_polynomial()
z1*z2^2*z3^3
Returns the list of the descents of the permutation p.
A descent of a permutation is an integer i such that p[i] > p[i+1]. With the final_descent option, the last position of a non empty permutation is also considered as a descent.
EXAMPLES:
sage: Permutation([1,4,3,2]).descents()
[1, 2]
sage: Permutation([1,4,3,2]).descents(final_descent=True)
[1, 2, 3]
Returns the composition corresponding to the descents of the permutation.
EXAMPLES:
sage: Permutation([1,3,2,4]).descents_composition()
[2, 2]
Returns a dictionary corresponding to the permutation.
EXAMPLES:
sage: p = Permutation([2,1,3])
sage: d = p.dict()
sage: d[1]
2
sage: d[2]
1
sage: d[3]
3
Returns a list of the fixed points of the permutation p.
EXAMPLES:
sage: Permutation([1,3,2,4]).fixed_points()
[1, 4]
sage: Permutation([1,2,3,4]).fixed_points()
[1, 2, 3, 4]
Returns the boolean answering the question ‘Is patt a pattern appearing in permutation p?’
EXAMPLES:
sage: Permutation([3,5,1,4,6,2]).has_pattern([1,3,2])
True
Returns the coset-type of self as a partition.
self must be a permutation of even size 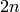 . The coset-type
determines the double class of the permutation, that is its image in
. The coset-type
determines the double class of the permutation, that is its image in
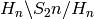 , where
, where 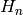 is the hyperoctahedral group
of order
is the hyperoctahedral group
of order  .
.
The coset-type is determined as follows. Consider the perfect matching
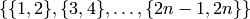 and its image by self and
draw them simultaneously as edges of a graph whose vertices are labeled
by
and its image by self and
draw them simultaneously as edges of a graph whose vertices are labeled
by 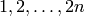 . The coset-type is the ordered sequence of the
semi-lengths of the loops of this graph (see [Mcd] for more details).
. The coset-type is the ordered sequence of the
semi-lengths of the loops of this graph (see [Mcd] for more details).
EXAMPLE:
sage: Permutation([3, 4, 6, 1, 5, 7, 2, 8]).hyperoctahedral_double_coset_type()
[3, 1]
sage: all([p.hyperoctahedral_double_coset_type() ==
... p.inverse().hyperoctahedral_double_coset_type()
... for p in Permutations(4)])
True
sage: Permutation([]).hyperoctahedral_double_coset_type()
[]
sage: Permutation([3,1,2]).hyperoctahedral_double_coset_type()
...
ValueError: [3, 1, 2] is a permutation of odd size and has no coset-type
REFERENCES:
[Mcd] I. G. Macdonald, Symmetric functions and Hall polynomials, Oxford University Press, second edition, 1995 (chapter VII).
Returns a list of the idescents of self, that is the list of the descents of self’s inverse.
With the final_descent option, the last position of a non empty permutation is also considered as a descent.
EXAMPLES:
sage: Permutation([1,4,3,2]).idescents()
[1, 2]
sage: Permutation([1,4,3,2]).idescents(final_descent=True)
[1, 2, 3]
Each position in self is mapped to -1 if it is an idescent and 1 if it is not an idescent.
EXAMPLES:
sage: Permutation([1,4,3,2]).idescents()
[1, 2]
sage: Permutation([1,4,3,2]).idescents_signature()
[1, -1, -1, 1]
Returns the inverse major index of the permutation self, which is the major index of the inverse of self.
The major index is the sum of the descents of p. Since our permutation indices are 0-based, we need to add one the number of descents.
EXAMPLES:
sage: Permutation([2,1,3]).imajor_index()
1
sage: Permutation([3,4,1,2]).imajor_index()
2
sage: Permutation([4,3,2,1]).imajor_index()
6
Returns the inverse of a permutation
EXAMPLES:
sage: Permutation([3,8,5,10,9,4,6,1,7,2]).inverse()
[8, 10, 1, 6, 3, 7, 9, 2, 5, 4]
sage: Permutation([2, 4, 1, 5, 3]).inverse()
[3, 1, 5, 2, 4]
Returns a list of the inversions of permutation p.
EXAMPLES:
sage: Permutation([3,2,4,1,5]).inversions()
[[0, 1], [0, 3], [1, 3], [2, 3]]
Returns True if the permutation p is even and false otherwise.
EXAMPLES:
sage: Permutation([1,2,3]).is_even()
True
sage: Permutation([2,1,3]).is_even()
False
Returns an the i-shift of self. If an i-shift of self can’t be performed, then None is returned.
An i-shift can be applied when i is not in between i-1 and i+1. The i-shift moves i to the other side, and leaves the relative positions of i-1 and i+1 in place.
EXAMPLES: Here, 2 is to the left of both 1 and 3. A 2-shift can be applied which moves the 2 to the right and leaves 1 and 3 in their same relative order.
sage: Permutation([2,1,3]).ishift(2)
[1, 3, 2]
Note that the movement is done in place:
sage: Permutation([2,4,1,3]).ishift(2)
[1, 4, 3, 2]
Since 2 is between 1 and 3 in [1,2,3], an 2-shift cannot be applied.
sage: Permutation([1,2,3]).ishift(2)
[1, 2, 3]
Returns an the i-switch of self. If an i-switch of self can’t be performed, then self is returned.
An i-shift can be applied when i is not in between i-1 and i+1. The i-shift moves i to the other side, and switches the relative positions of i-1 and i+1 in place.
EXAMPLES: Here, 2 is to the left of both 1 and 3. A 2-switch can be applied which moves the 2 to the right and switches the relative order between 1 and 3.
sage: Permutation([2,1,3]).iswitch(2)
[3, 1, 2]
Note that the movement is done in place:
sage: Permutation([2,4,1,3]).iswitch(2)
[3, 4, 1, 2]
Since 2 is between 1 and 3 in [1,2,3], an 2-switch cannot be applied.
sage: Permutation([1,2,3]).iswitch(2)
[1, 2, 3]
Returns the right standard tableau after performing the RSK algorithm on self.
EXAMPLES:
sage: Permutation([1,4,3,2]).left_tableau()
[[1, 2], [3], [4]]
Returns the length of a permutation p. The length is given by the number of inversions of p.
EXAMPLES:
sage: Permutation([5, 1, 3, 2, 4]).length()
5
Returns the length of the longest increasing subsequences of the permutation p.
EXAMPLES:
sage: Permutation([2,3,1,4]).longest_increasing_subsequence_length()
3
sage: all([i.longest_increasing_subsequence_length() == len(i.robinson_schensted()[0][0]) for i in Permutations(5)])
True
Returns the list of the longest increasing subsequences of the permutation p.
Note
The algorithm is not optimal.
EXAMPLES:
sage: Permutation([2,3,4,1]).longest_increasing_subsequences()
[[2, 3, 4]]
sage: Permutation([5, 7, 1, 2, 6, 4, 3]).longest_increasing_subsequences()
[[1, 2, 6], [1, 2, 4], [1, 2, 3]]
Returns the major index of the permutation p.
The major index is the sum of the descents of p. Since our permutation indices are 0-based, we need to add one the number of descents.
EXAMPLES:
sage: Permutation([2,1,3]).major_index()
1
sage: Permutation([3,4,1,2]).major_index()
2
sage: Permutation([4,3,2,1]).major_index()
6
Returns the permutation that follows p in lexicographic order. If p is the last permutation, then next returns false.
EXAMPLES:
sage: p = Permutation([1, 3, 2])
sage: p.next()
[2, 1, 3]
sage: p = Permutation([4,3,2,1])
sage: p.next()
False
Returns the number of descents of the permutation p.
EXAMPLES:
sage: Permutation([1,4,3,2]).number_of_descents()
2
sage: Permutation([1,4,3,2]).number_of_descents(final_descent=True)
3
Returns the number of fixed points of the permutation p.
EXAMPLES:
sage: Permutation([1,3,2,4]).number_of_fixed_points()
2
sage: Permutation([1,2,3,4]).number_of_fixed_points()
4
Returns the number of descents of the permutation p.
EXAMPLES:
sage: Permutation([1,4,3,2]).number_of_idescents()
2
sage: Permutation([1,4,3,2]).number_of_idescents(final_descent=True)
3
Returns the number of inversions in the permutation p.
An inversion of a permutation is a pair of elements (p[i],p[j]) with i < j and p[i] > p[j].
REFERENCES:
EXAMPLES:
sage: Permutation([3,2,4,1,5]).number_of_inversions()
4
sage: Permutation([1, 2, 6, 4, 7, 3, 5]).number_of_inversions()
6
Returns the number of peaks of the permutation p.
A peak of a permutation is an integer i such that p[i-1] < p[i] and p[i] > p[i+1].
EXAMPLES:
sage: Permutation([1,3,2,4,5]).number_of_peaks()
1
sage: Permutation([4,1,3,2,6,5]).number_of_peaks()
2
Returns the number of recoils of the permutation p.
EXAMPLES:
sage: Permutation([1,4,3,2]).number_of_recoils()
2
Returns the number of saliances of the permutation p.
EXAMPLES:
sage: Permutation([2,3,1,5,4]).number_of_saliances()
2
sage: Permutation([5,4,3,2,1]).number_of_saliances()
5
Returns the list of positions where the pattern patt appears in p.
EXAMPLES:
sage: Permutation([3,5,1,4,6,2]).pattern_positions([1,3,2])
[[0, 1, 3], [2, 3, 5], [2, 4, 5]]
Returns a list of the peaks of the permutation p.
A peak of a permutation is an integer i such that p[i-1] < p[i] and p[i] > p[i+1].
EXAMPLES:
sage: Permutation([1,3,2,4,5]).peaks()
[1]
sage: Permutation([4,1,3,2,6,5]).peaks()
[2, 4]
Returns a list of permutations greater than or equal to p in the permutohedron order.
By default, the computations are done in the right permutohedron. If you pass the option side=’left’, then they will be done in the left permutohedron.
EXAMPLES:
sage: Permutation([4,2,1,3]).permutohedron_greater()
[[4, 2, 1, 3], [4, 2, 3, 1], [4, 3, 2, 1]]
sage: Permutation([4,2,1,3]).permutohedron_greater(side='left')
[[4, 2, 1, 3], [4, 3, 1, 2], [4, 3, 2, 1]]
Returns True if self is less than p2 in the permutohedron order.
By default, the computations are done in the right permutohedron. If you pass the option side=’left’, then they will be done in the left permutohedron.
EXAMPLES:
sage: p = Permutation([3,2,1,4])
sage: p.permutohedron_lequal(Permutation([4,2,1,3]))
False
sage: p.permutohedron_lequal(Permutation([4,2,1,3]), side='left')
True
Returns a list of the permutations strictly smaller than p in the permutohedron order such that there is no permutation between one of those and p.
By default, the computations are done in the right permutohedron. If you pass the option side=’left’, then they will be done in the left permutohedron.
EXAMPLES:
sage: p = Permutation([4,2,1,3])
sage: p.permutohedron_pred()
[[2, 4, 1, 3], [4, 1, 2, 3]]
sage: p.permutohedron_pred(side='left')
[[4, 1, 2, 3], [3, 2, 1, 4]]
Returns a list of permutations smaller than or equal to p in the permutohedron order.
By default, the computations are done in the right permutohedron. If you pass the option side=’left’, then they will be done in the left permutohedron.
EXAMPLES:
sage: Permutation([4,2,1,3]).permutohedron_smaller()
[[1, 2, 3, 4],
[1, 2, 4, 3],
[1, 4, 2, 3],
[2, 1, 3, 4],
[2, 1, 4, 3],
[2, 4, 1, 3],
[4, 1, 2, 3],
[4, 2, 1, 3]]
sage: Permutation([4,2,1,3]).permutohedron_smaller(side='left')
[[1, 2, 3, 4],
[1, 3, 2, 4],
[2, 1, 3, 4],
[2, 3, 1, 4],
[3, 1, 2, 4],
[3, 2, 1, 4],
[4, 1, 2, 3],
[4, 2, 1, 3]]
Returns a list of the permutations strictly greater than p in the permutohedron order such that there is no permutation between one of those and p.
By default, the computations are done in the right permutohedron. If you pass the option side=’left’, then they will be done in the left permutohedron.
EXAMPLES:
sage: p = Permutation([4,2,1,3])
sage: p.permutohedron_succ()
[[4, 2, 3, 1]]
sage: p.permutohedron_succ(side='left')
[[4, 3, 1, 2]]
Returns the permutation that comes directly before p in lexicographic order. If p is the first permutation, then it returns False.
EXAMPLES:
sage: p = Permutation([1,2,3])
sage: p.prev()
False
sage: p = Permutation([1,3,2])
sage: p.prev()
[1, 2, 3]
Returns the rank of a permutation in lexicographic ordering.
EXAMPLES:
sage: Permutation([1,2,3]).rank()
0
sage: Permutation([1, 2, 4, 6, 3, 5]).rank()
10
sage: perms = Permutations(6).list()
sage: [p.rank() for p in perms ] == range(factorial(6))
True
Returns the list of the positions of the recoils of the permutation p.
A recoil of a permutation is an integer i such that i+1 is to the left of it.
EXAMPLES:
sage: Permutation([1,4,3,2]).recoils()
[2, 3]
Returns the composition corresponding to recoils of the permutation.
EXAMPLES:
sage: Permutation([1,3,2,4]).recoils_composition()
[3]
Returns the reduced word of a permutation.
EXAMPLES:
sage: Permutation([3,5,4,6,2,1]).reduced_word()
[2, 1, 4, 3, 2, 4, 3, 5, 4, 5]
Returns a lexicographically minimal reduced word of a permutation.
EXAMPLES:
sage: Permutation([3,4,2,1]).reduced_word_lexmin()
[1, 2, 1, 3, 2]
Returns a list of the reduced words of the permutation p.
EXAMPLES:
sage: Permutation([2,1,3]).reduced_words()
[[1]]
sage: Permutation([3,1,2]).reduced_words()
[[2, 1]]
sage: Permutation([3,2,1]).reduced_words()
[[1, 2, 1], [2, 1, 2]]
sage: Permutation([3,2,4,1]).reduced_words()
[[1, 2, 3, 1], [1, 2, 1, 3], [2, 1, 2, 3]]
Returns the permutation obtained by removing any fixed points at the end of self.
EXAMPLES:
sage: Permutation([2,1,3]).remove_extra_fixed_points()
[2, 1]
sage: Permutation([1,2,3,4]).remove_extra_fixed_points()
[1]
Returns the permutation obtained by reversing the list.
EXAMPLES:
sage: Permutation([3,4,1,2]).reverse()
[2, 1, 4, 3]
sage: Permutation([1,2,3,4,5]).reverse()
[5, 4, 3, 2, 1]
Returns the right standard tableau after performing the RSK algorithm on self.
EXAMPLES:
sage: Permutation([1,4,3,2]).right_tableau()
[[1, 2], [3], [4]]
Returns the pair of standard tableaux obtained by running the Robinson-Schensted Algorithm on self.
EXAMPLES:
sage: Permutation([6,2,3,1,7,5,4]).robinson_schensted()
[[[1, 3, 4], [2, 5], [6, 7]], [[1, 3, 5], [2, 6], [4, 7]]]
It also works in the case of repeated letters. In this case only the second tableau is standard:
sage: Permutation([2,3,3,2,1,3,2,3]).robinson_schensted()
[[[1, 2, 2, 3, 3], [2, 3], [3]], [[1, 2, 3, 6, 8], [4, 7], [5]]]
TESTS:
The empty permutation:
sage: p = Permutation([])
sage: p.robinson_schensted()
[[], []]
Returns a list of the runs in the permutation p.
REFERENCES:
EXAMPLES:
sage: Permutation([1,2,3,4]).runs()
[[1, 2, 3, 4]]
sage: Permutation([4,3,2,1]).runs()
[[4], [3], [2], [1]]
sage: Permutation([2,4,1,3]).runs()
[[2, 4], [1, 3]]
Returns a list of the saliances of the permutation p.
A saliance of a permutation p is an integer i such that p[i] > p[j] for all j > i.
EXAMPLES:
sage: Permutation([2,3,1,5,4]).saliances()
[3, 4]
sage: Permutation([5,4,3,2,1]).saliances()
[0, 1, 2, 3, 4]
Returns the signature of a permutation.
EXAMPLES:
sage: Permutation([4, 2, 3, 1, 5]).signature()
-1
Returns the permutation p as a list of disjoint cycles.
If singletons=False is given, don’t returns the singletons in the list of cycles.
EXAMPLES:
sage: Permutation([2,1,3,4]).to_cycles() [(1, 2), (3,), (4,)] sage: Permutation([2,1,3,4]).to_cycles(singletons=False) [(1, 2)]The algorithm is of complexity
where
is the size of the given permutation.
TESTS:
sage: from sage.combinat.permutation import from_cycles sage: all(from_cycles(n, p.to_cycles()) == p ... for n in range(6) for p in Permutations(n)) True sage: size = 10000 sage: sample = (Permutations(size).random_element() for i in range(5)) sage: all(from_cycles(size, p.to_cycles()) == p for p in sample) TrueNote: there is an alternative implementation called _to_cycle_set which could be slightly (10%) faster for some input (typically for permutations of size in the range [100, 10000]. You can run the following benchmarks. For small permutations:
sage: for size in range(9): # not tested ... print size ... lp = Permutations(size).list() ... timeit('[p.to_cycles(False) for p in lp]') ... timeit('[p._to_cycles_set(False) for p in lp]') ... timeit('[p._to_cycles_list(False) for p in lp]') ... timeit('[p._to_cycles_orig(False) for p in lp]')
and larger one:
sage: for size in [10, 20, 50, 75, 100, 200, 500, 1000, # not tested
... 2000, 5000, 10000, 15000, 20000, 30000,
... 50000, 80000, 100000]:
... print(size)
... lp = [Permutations(size).random_element() for i in range(20)]
... timeit("[p.to_cycles() for p in lp]")
... timeit("[p._to_cycles_set() for p in lp]")
... timeit("[p._to_cycles_list() for p in lp]") # not tested
Returns the inversion vector of a permutation p.
If 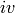 is the inversion vector, then
is the inversion vector, then ![iv[i]](../../_images/math/3435313d3f1d454bbc18cf6ae5ee49cfbd941bec.png) is the number of elements
larger than
is the number of elements
larger than  that appear to the left of
that appear to the left of  in the permutation.
in the permutation.
The algorithm is of complexity 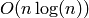 where
where  is the size of
the given permutation.
is the size of
the given permutation.
EXAMPLES:
sage: Permutation([5,9,1,8,2,6,4,7,3]).to_inversion_vector()
[2, 3, 6, 4, 0, 2, 2, 1, 0]
sage: Permutation([8,7,2,1,9,4,6,5,10,3]).to_inversion_vector()
[3, 2, 7, 3, 4, 3, 1, 0, 0, 0]
sage: Permutation([3,2,4,1,5]).to_inversion_vector()
[3, 1, 0, 0, 0]
TESTS:
sage: from sage.combinat.permutation import from_inversion_vector
sage: all(from_inversion_vector(p.to_inversion_vector()) == p
... for n in range(6) for p in Permutations(n))
True
sage: P = Permutations(1000)
sage: sample = (P.random_element() for i in range(5))
sage: all(from_inversion_vector(p.to_inversion_vector()) == p
... for p in sample)
True
Returns the Lehmer cocode of p.
EXAMPLES:
sage: p = Permutation([2,1,3])
sage: p.to_lehmer_cocode()
[0, 1, 0]
sage: q = Permutation([3,1,2])
sage: q.to_lehmer_cocode()
[0, 1, 1]
Returns the Lehmer code of the permutation p.
![c[i]](../../_images/math/885cb8db7e7f67fdaeac3fcee3a3da268c6a058d.png) is the number of
is the number of 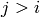 such that
such that 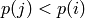 .
.
EXAMPLES:
sage: p = Permutation([2,1,3])
sage: p.to_lehmer_code()
[1, 0, 0]
sage: q = Permutation([3,1,2])
sage: q.to_lehmer_code()
[2, 0, 0]
TESTS:
sage: from sage.combinat.permutation import from_lehmer_code
sage: all(from_lehmer_code(p.to_lehmer_code()) == p
... for n in range(6) for p in Permutations(n))
True
sage: P = Permutations(1000)
sage: sample = (P.random_element() for i in range(5))
sage: all(from_lehmer_code(p.to_lehmer_code()) == p
... for p in sample)
True
Returns the major code of the permutation p, which is defined as the list [m1-m2, m2-m3,..,mn] where mi := maj(pi) is the major indices of the permutation math obtained by erasing the letters smaller than math in p.
REFERENCES:
EXAMPLES:
sage: Permutation([9,3,5,7,2,1,4,6,8]).to_major_code()
[5, 0, 1, 0, 1, 2, 0, 1, 0]
sage: Permutation([2,8,4,3,6,7,9,5,1]).to_major_code()
[8, 3, 3, 1, 4, 0, 1, 0, 0]
Returns a matrix representing the permutation.
EXAMPLES:
sage: Permutation([1,2,3]).to_matrix()
[1 0 0]
[0 1 0]
[0 0 1]
sage: Permutation([1,3,2]).to_matrix()
[1 0 0]
[0 0 1]
[0 1 0]
Notice that matrix multiplication corresponds to permutation multiplication only when the permutation option mult=’r2l’
sage: PermutationOptions(mult='r2l')
sage: p = Permutation([2,1,3])
sage: q = Permutation([3,1,2])
sage: (p*q).to_matrix()
[0 0 1]
[0 1 0]
[1 0 0]
sage: p.to_matrix()*q.to_matrix()
[0 0 1]
[0 1 0]
[1 0 0]
sage: PermutationOptions(mult='l2r')
sage: (p*q).to_matrix()
[1 0 0]
[0 0 1]
[0 1 0]
Returns a PermutationGroupElement equal to self.
EXAMPLES:
sage: Permutation([2,1,4,3]).to_permutation_group_element()
(1,2)(3,4)
sage: Permutation([1,2,3]).to_permutation_group_element()
()
Returns a tableau of shape shape with the entries in self.
EXAMPLES:
sage: Permutation([3,4,1,2,5]).to_tableau_by_shape([3,2])
[[1, 2, 5], [3, 4]]
sage: Permutation([3,4,1,2,5]).to_tableau_by_shape([3,2]).to_permutation()
[3, 4, 1, 2, 5]
Returns all the numbers self[i] such that self[i] = i+1.
EXAMPLES:
sage: Permutation([1,4,3,2,5]).weak_excedences()
[1, 4, 3, 5]
Returns a combinatorial class of permutations.
Permutations(n) returns the class of permutations of n, if n is an integer, list, set, or string.
Permutations(n, k) returns the class of permutations of n (where n is any of the above things) of length k; k must be an integer.
Valid keyword arguments are: ‘descents’, ‘bruhat_smaller’, ‘bruhat_greater’, ‘recoils_finer’, ‘recoils_fatter’, ‘recoils’, and ‘avoiding’. With the exception of ‘avoiding’, you cannot specify n or k along with a keyword.
Permutations(descents=list) returns the class of permutations with descents in the positions specified by ‘list’.
Permutations(bruhat_smaller,greater=p) returns the class of permutations smaller or greater, respectively, than the given permutation in Bruhat order.
Permutations(recoils=p) returns the class of permutations whose recoils composition is p.
Permutations(recoils_fatter,finer=p) returns the class of permutations whose recoils composition is fatter or finer, respectively, than the given permutation.
Permutations(n, avoiding=P) returns the class of permutations of n avoiding P. Here P may be a single permutation or a list of permutations; the returned class will avoid all patterns in P.
EXAMPLES:
sage: p = Permutations(3); p
Standard permutations of 3
sage: p.list()
[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]
sage: p = Permutations(3, 2); p
Permutations of {1,...,3} of length 2
sage: p.list()
[[1, 2], [1, 3], [2, 1], [2, 3], [3, 1], [3, 2]]
sage: p = Permutations(['c', 'a', 't']); p
Permutations of the set ['c', 'a', 't']
sage: p.list()
[['c', 'a', 't'],
['c', 't', 'a'],
['a', 'c', 't'],
['a', 't', 'c'],
['t', 'c', 'a'],
['t', 'a', 'c']]
sage: p = Permutations(['c', 'a', 't'], 2); p
Permutations of the set ['c', 'a', 't'] of length 2
sage: p.list()
[['c', 'a'], ['c', 't'], ['a', 'c'], ['a', 't'], ['t', 'c'], ['t', 'a']]
sage: p = Permutations([1,1,2]); p
Permutations of the multi-set [1, 1, 2]
sage: p.list()
[[1, 1, 2], [1, 2, 1], [2, 1, 1]]
sage: p = Permutations([1,1,2], 2); p
Permutations of the multi-set [1, 1, 2] of length 2
sage: p.list()
[[1, 1], [1, 2], [2, 1]]
sage: p = Permutations(descents=[1,3]); p
Standard permutations of 4 with descents [1, 3]
sage: p.list()
[[1, 3, 2, 4], [1, 4, 2, 3], [2, 3, 1, 4], [2, 4, 1, 3], [3, 4, 1, 2]]
sage: p = Permutations(bruhat_smaller=[1,3,2,4]); p
Standard permutations that are less than or equal to [1, 3, 2, 4] in the Bruhat order
sage: p.list()
[[1, 2, 3, 4], [1, 3, 2, 4]]
sage: p = Permutations(bruhat_greater=[4,2,3,1]); p
Standard permutations that are greater than or equal to [4, 2, 3, 1] in the Bruhat order
sage: p.list()
[[4, 2, 3, 1], [4, 3, 2, 1]]
sage: p = Permutations(recoils_finer=[2,1]); p
Standard permutations whose recoils composition is finer than [2, 1]
sage: p.list()
[[1, 2, 3], [1, 3, 2], [3, 1, 2]]
sage: p = Permutations(recoils_fatter=[2,1]); p
Standard permutations whose recoils composition is fatter than [2, 1]
sage: p.list()
[[1, 3, 2], [3, 1, 2], [3, 2, 1]]
sage: p = Permutations(recoils=[2,1]); p
Standard permutations whose recoils composition is [2, 1]
sage: p.list()
[[1, 3, 2], [3, 1, 2]]
sage: p = Permutations(4, avoiding=[1,3,2]); p
Standard permutations of 4 avoiding [1, 3, 2]
sage: p.list()
[[4, 1, 2, 3],
[4, 2, 1, 3],
[4, 2, 3, 1],
[4, 3, 1, 2],
[4, 3, 2, 1],
[3, 4, 1, 2],
[3, 4, 2, 1],
[2, 3, 4, 1],
[3, 2, 4, 1],
[1, 2, 3, 4],
[2, 1, 3, 4],
[2, 3, 1, 4],
[3, 1, 2, 4],
[3, 2, 1, 4]]
sage: p = Permutations(5, avoiding=[[3,4,1,2], [4,2,3,1]]); p
Standard permutations of 5 avoiding [[3, 4, 1, 2], [4, 2, 3, 1]]
sage: p.cardinality()
88
sage: p.random_element()
[5, 1, 2, 4, 3]
Bases: sage.combinat.combinat.CombinatorialClass
EXAMPLES:
sage: Permutations([1,2,2]).cardinality()
3
Bases: sage.combinat.combinat.CombinatorialClass
EXAMPLES:
sage: Permutations([1,2,2],2).list()
[[1, 2], [2, 1], [2, 2]]
Bases: sage.combinat.combinat.CombinatorialClass
EXAMPLES:
sage: Permutations(3,0).cardinality()
1
sage: Permutations(3,1).cardinality()
3
sage: Permutations(3,2).cardinality()
6
sage: Permutations(3,3).cardinality()
6
sage: Permutations(3,4).cardinality()
0
EXAMPLES:
sage: Permutations(3,2).random_element()
[0, 1]
Bases: sage.combinat.combinat.CombinatorialClass
EXAMPLES:
sage: Permutations([1,2,3]).cardinality()
6
EXAMPLES:
sage: Permutations([1,2,3]).random_element()
[1, 2, 3]
Bases: sage.combinat.combinat.CombinatorialClass
EXAMPLES:
sage: Permutations([1,2,3],2).random_element()
[1, 2]
Bases: sage.combinat.combinat.InfiniteAbstractCombinatorialClass
Bases: sage.combinat.combinat.CombinatorialClass
EXAMPLES:
sage: Permutations(3, avoiding=[1,2]).list()
[[3, 2, 1]]
Bases: sage.combinat.combinat.CombinatorialClass
EXAMPLES:
sage: Permutations(5, avoiding=[1, 2, 3]).cardinality()
42
sage: len( Permutations(5, avoiding=[1, 2, 3]).list() )
42
Bases: sage.combinat.combinat.CombinatorialClass
EXAMPLES:
sage: Permutations(5, avoiding=[1, 3, 2]).cardinality()
42
sage: len( Permutations(5, avoiding=[1, 3, 2]).list() )
42
Bases: sage.combinat.combinat.CombinatorialClass
EXAMPLES:
sage: Permutations(3, avoiding=[2,1]).list()
[[1, 2, 3]]
Bases: sage.combinat.combinat.CombinatorialClass
EXAMPLES:
sage: Permutations(5, avoiding=[2, 1, 3]).cardinality()
42
sage: len( Permutations(5, avoiding=[2, 1, 3]).list() )
42
Bases: sage.combinat.combinat.CombinatorialClass
EXAMPLES:
sage: Permutations(5, avoiding=[2, 3, 1]).cardinality()
42
sage: len( Permutations(5, avoiding=[2, 3, 1]).list() )
42
Bases: sage.combinat.combinat.CombinatorialClass
EXAMPLES:
sage: Permutations(5, avoiding=[3, 1, 2]).cardinality()
42
sage: len( Permutations(5, avoiding=[3, 1, 2]).list() )
42
Bases: sage.combinat.combinat.CombinatorialClass
EXAMPLES:
sage: Permutations(5, avoiding=[3, 2, 1]).cardinality()
42
sage: len( Permutations(5, avoiding=[3, 2, 1]).list() )
42
Bases: sage.combinat.combinat.CombinatorialClass
Returns a list of permutations greater than or equal to p in the Bruhat order.
EXAMPLES:
sage: Permutations(bruhat_greater=[4,1,2,3]).list()
[[4, 1, 2, 3],
[4, 1, 3, 2],
[4, 2, 1, 3],
[4, 2, 3, 1],
[4, 3, 1, 2],
[4, 3, 2, 1]]
Bases: sage.combinat.combinat.CombinatorialClass
Returns a list of permutations smaller than or equal to p in the Bruhat order.
EXAMPLES:
sage: Permutations(bruhat_smaller=[4,1,2,3]).list()
[[1, 2, 3, 4],
[1, 2, 4, 3],
[1, 3, 2, 4],
[1, 4, 2, 3],
[2, 1, 3, 4],
[2, 1, 4, 3],
[3, 1, 2, 4],
[4, 1, 2, 3]]
Bases: sage.combinat.combinat.CombinatorialClass
Returns the first permutation with descents d.
EXAMPLES:
sage: Permutations(descents=([1,0,4,8],12)).first()
[3, 2, 1, 4, 6, 5, 7, 8, 10, 9, 11, 12]
Returns the last permutation with descents d.
EXAMPLES:
sage: Permutations(descents=([1,0,4,8],12)).last()
[12, 11, 8, 9, 10, 4, 5, 6, 7, 1, 2, 3]
Returns a list of all the permutations that have the descents d.
EXAMPLES:
sage: Permutations(descents=([2,4,0],5)).list()
[[2, 1, 4, 3, 5],
[2, 1, 5, 3, 4],
[3, 1, 4, 2, 5],
[3, 1, 5, 2, 4],
[4, 1, 3, 2, 5],
[5, 1, 3, 2, 4],
[4, 1, 5, 2, 3],
[5, 1, 4, 2, 3],
[3, 2, 4, 1, 5],
[3, 2, 5, 1, 4],
[4, 2, 3, 1, 5],
[5, 2, 3, 1, 4],
[4, 2, 5, 1, 3],
[5, 2, 4, 1, 3],
[4, 3, 5, 1, 2],
[5, 3, 4, 1, 2]]
Bases: sage.combinat.combinat.CombinatorialClass
EXAMPLES:
sage: Permutations(0).cardinality()
1
sage: Permutations(3).cardinality()
6
sage: Permutations(4).cardinality()
24
Returns the identity permutation of length n.
EXAMPLES:
sage: Permutations(4).identity()
[1, 2, 3, 4]
sage: Permutations(0).identity()
[]
EXAMPLES:
sage: Permutations(4).random_element()
[1, 2, 4, 3]
EXAMPLES:
sage: SP3 = Permutations(3)
sage: map(SP3.rank, SP3)
[0, 1, 2, 3, 4, 5]
sage: SP0 = Permutations(0)
sage: map(SP0.rank, SP0)
[0]
EXAMPLES:
sage: SP3 = Permutations(3)
sage: l = map(SP3.unrank, range(6))
sage: l == SP3.list()
True
sage: SP0 = Permutations(0)
sage: l = map(SP0.unrank, range(1))
sage: l == SP0.list()
True
Bases: sage.combinat.combinat.CombinatorialClass
Returns a list of all of the permutations whose recoils composition is equal to recoils.
EXAMPLES:
sage: Permutations(recoils=[2,2]).list()
[[1, 3, 2, 4], [1, 3, 4, 2], [3, 1, 2, 4], [3, 1, 4, 2], [3, 4, 1, 2]]
Bases: sage.combinat.combinat.CombinatorialClass
Returns a list of all of the permutations whose recoils composition is fatter than recoils.
EXAMPLES:
sage: Permutations(recoils_fatter=[2,2]).list()
[[1, 3, 2, 4],
[1, 3, 4, 2],
[1, 4, 3, 2],
[3, 1, 2, 4],
[3, 1, 4, 2],
[3, 2, 1, 4],
[3, 2, 4, 1],
[3, 4, 1, 2],
[3, 4, 2, 1],
[4, 1, 3, 2],
[4, 3, 1, 2],
[4, 3, 2, 1]]
Bases: sage.combinat.combinat.CombinatorialClass
Returns a list of all of the permutations whose recoils composition is finer than recoils.
EXAMPLES:
sage: Permutations(recoils_finer=[2,2]).list()
[[1, 2, 3, 4],
[1, 3, 2, 4],
[1, 3, 4, 2],
[3, 1, 2, 4],
[3, 1, 4, 2],
[3, 4, 1, 2]]
Returns the positive sum of permutations corresponding to the bistochastic matrix.
A stochastic matrix is a matrix with nonnegative real entries such that the sum of the elements of any row is equal to 1. A bistochastic matrix is a stochastic matrix whose transpose matrix is also stochastic ( there are conditions both on the rows and on the columns ).
According to the Birkhoff-von Neumann Theorem, any bistochastic matrix can be written as a positive sum of permutation matrices, which also means that the polytope of bistochastic matrices is integer.
As a non-bistochastic matrix can obviously not be written as a sum of permutations, this theorem is an equivalence.
This function, given a bistochastic matrix, returns the corresponding decomposition.
INPUT:
OUTPUT:
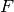 -module
( where
-module
( where 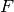 is the ground ring of the given matrix ) whose basis is
indexed by the permutations.
is the ground ring of the given matrix ) whose basis is
indexed by the permutations.Note
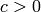 such that
such that 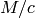 is bistochastic.
is bistochastic.EXAMPLE:
We create a bistochastic matrix from a convex sum of permutations, then try to deduce the decomposition from the matrix
sage: from sage.combinat.permutation import bistochastic_as_sum_of_permutations
sage: L = []
sage: L.append((9,Permutation([4, 1, 3, 5, 2])))
sage: L.append((6,Permutation([5, 3, 4, 1, 2])))
sage: L.append((3,Permutation([3, 1, 4, 2, 5])))
sage: L.append((2,Permutation([1, 4, 2, 3, 5])))
sage: M = sum([c * p.to_matrix() for (c,p) in L])
sage: decomp = bistochastic_as_sum_of_permutations(M)
sage: print decomp
2*B[[1, 4, 2, 3, 5]] + 3*B[[3, 1, 4, 2, 5]] + 9*B[[4, 1, 3, 5, 2]] + 6*B[[5, 3, 4, 1, 2]]
An exception is raised when the matrix is not positive and bistochastic:
sage: M = Matrix([[2,3],[2,2]])
sage: decomp = bistochastic_as_sum_of_permutations(M)
...
ValueError: The matrix is not bistochastic
sage: bistochastic_as_sum_of_permutations(Matrix(GF(7), 2, [2,1,1,2]))
...
ValueError: The base ring of the matrix must have a coercion map to RR
sage: bistochastic_as_sum_of_permutations(Matrix(ZZ, 2, [2,-1,-1,2]))
...
ValueError: The matrix should have nonnegative entries
Returns True if p1 is less than p2 in the Bruhat order.
Algorithm from mupad-combinat.
EXAMPLES:
sage: import sage.combinat.permutation as permutation
sage: permutation.bruhat_lequal([2,4,3,1],[3,4,2,1])
True
Computes the smallest element of a descent class having a descent decomposition dc.
EXAMPLES:
sage: import sage.combinat.permutation as permutation
sage: permutation.descents_composition_first([1,1,3,4,3])
[3, 2, 1, 4, 6, 5, 7, 8, 10, 9, 11, 12]
Returns the largest element of a descent class having a descent decomposition dc.
EXAMPLES:
sage: import sage.combinat.permutation as permutation
sage: permutation.descents_composition_last([1,1,3,4,3])
[12, 11, 8, 9, 10, 4, 5, 6, 7, 1, 2, 3]
Returns a list of all the permutations that have a descent compositions dc.
EXAMPLES:
sage: import sage.combinat.permutation as permutation
sage: permutation.descents_composition_list([1,2,2])
[[2, 1, 4, 3, 5],
[2, 1, 5, 3, 4],
[3, 1, 4, 2, 5],
[3, 1, 5, 2, 4],
[4, 1, 3, 2, 5],
[5, 1, 3, 2, 4],
[4, 1, 5, 2, 3],
[5, 1, 4, 2, 3],
[3, 2, 4, 1, 5],
[3, 2, 5, 1, 4],
[4, 2, 3, 1, 5],
[5, 2, 3, 1, 4],
[4, 2, 5, 1, 3],
[5, 2, 4, 1, 3],
[4, 3, 5, 1, 2],
[5, 3, 4, 1, 2]]
Returns the permutation corresponding to cycles.
EXAMPLES:
sage: import sage.combinat.permutation as permutation
sage: permutation.from_cycles(4, [[1,2]])
[2, 1, 3, 4]
Returns the permutation corresponding to inversion vector iv.
EXAMPLES:
sage: import sage.combinat.permutation as permutation
sage: permutation.from_inversion_vector([3,1,0,0,0])
[3, 2, 4, 1, 5]
sage: permutation.from_inversion_vector([2,3,6,4,0,2,2,1,0])
[5, 9, 1, 8, 2, 6, 4, 7, 3]
Returns the permutation with Lehmer code lehmer.
EXAMPLES:
sage: import sage.combinat.permutation as permutation
sage: Permutation([2,1,5,4,3]).to_lehmer_code()
[1, 0, 2, 1, 0]
sage: permutation.from_lehmer_code(_)
[2, 1, 5, 4, 3]
Returns the permutation corresponding to major code mc.
REFERENCES:
EXAMPLES:
sage: import sage.combinat.permutation as permutation
sage: permutation.from_major_code([5, 0, 1, 0, 1, 2, 0, 1, 0])
[9, 3, 5, 7, 2, 1, 4, 6, 8]
sage: permutation.from_major_code([8, 3, 3, 1, 4, 0, 1, 0, 0])
[2, 8, 4, 3, 6, 7, 9, 5, 1]
sage: Permutation([2,1,6,4,7,3,5]).to_major_code()
[3, 2, 0, 2, 2, 0, 0]
sage: permutation.from_major_code([3, 2, 0, 2, 2, 0, 0])
[2, 1, 6, 4, 7, 3, 5]
Returns a Permutation give a PermutationGroupElement pge.
EXAMPLES:
sage: import sage.combinat.permutation as permutation
sage: pge = PermutationGroupElement([(1,2),(3,4)])
sage: permutation.from_permutation_group_element(pge)
[2, 1, 4, 3]
Returns the permutation with the specified lexicographic rank. The permutation is of the set [1,...,n].
The permutation is computed without iterating through all of the permutations with lower rank. This makes it efficient for large permutations.
EXAMPLES:
sage: import sage.combinat.permutation as permutation
sage: Permutation([3, 6, 5, 4, 2, 1]).rank()
359
sage: [permutation.from_rank(3, i) for i in range(6)]
[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]
sage: Permutations(6)[10]
[1, 2, 4, 6, 3, 5]
sage: permutation.from_rank(6,10)
[1, 2, 4, 6, 3, 5]
Returns the permutation corresponding to the reduced word rw.
EXAMPLES:
sage: import sage.combinat.permutation as permutation
sage: permutation.from_reduced_word([3,2,3,1,2,3,1])
[3, 4, 2, 1]
sage: permutation.from_reduced_word([])
[]
Returns True if p1 is less than p2in the permutohedron order.
By default, the computations are done in the right permutohedron. If you pass the option side=’left’, then they will be done in the left permutohedron.
EXAMPLES:
sage: import sage.combinat.permutation as permutation
sage: permutation.permutohedron_lequal(Permutation([3,2,1,4]),Permutation([4,2,1,3]))
False
sage: permutation.permutohedron_lequal(Permutation([3,2,1,4]),Permutation([4,2,1,3]), side='left')
True
Returns the permutation corresponding to the pair of tableaux 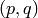 using the inverse of Robinson-Schensted algorithm.
using the inverse of Robinson-Schensted algorithm.
INPUT:
- p, q: two tableaux of the same shape and where q is standard.
EXAMPLES:
sage: from sage.combinat.permutation import robinson_schensted_inverse
sage: t1 = Tableau([[1, 2, 5], [3], [4]])
sage: t2 = Tableau([[1, 2, 3], [4], [5]])
sage: robinson_schensted_inverse(t1, t2)
[1, 4, 5, 3, 2]
sage: robinson_schensted_inverse(t1, t1)
[1, 4, 3, 2, 5]
sage: robinson_schensted_inverse(t2, t2)
[1, 2, 5, 4, 3]
sage: robinson_schensted_inverse(t2, t1)
[1, 5, 4, 2, 3]
If the first tableau is semistandard:
sage: p = Tableau([[1,2,2]]); q = Tableau([[1,2,3]])
sage: robinson_schensted_inverse(p, q)
[1, 2, 2]
sage: _.robinson_schensted()
[[[1, 2, 2]], [[1, 2, 3]]]
Note that currently the constructor of Tableau accept as input lists that are not even tableaux but only filling of a partition diagram. This feature should not be used with robinson_schensted_inverse.
TESTS:
From empty tableaux:
sage: robinson_schensted_inverse(Tableau([]), Tableau([]))
[]
This function is the inverse of robinson_shensted:
sage: f = lambda p: robinson_schensted_inverse(*p.robinson_schensted())
sage: all(p == f(p) for n in range(7) for p in Permutations(n))
True
sage: n = ZZ.random_element(200)
sage: p = Permutations(n).random_element()
sage: is_fine = True if p == f(p) else p ; is_fine
True
Both tableaux must be of the same shape:
sage: robinson_schensted_inverse(Tableau([[1,2,3]]), Tableau([[1,2]]))
...
ValueError: p(=[[1, 2, 3]]) and q(=[[1, 2]]) must have the same shape
The second tableau must be standard:
sage: robinson_schensted_inverse(Tableau([[1,2,3]]), Tableau([[1,3,2]]))
...
ValueError: q(=[[1, 3, 2]]) must be standard
Returns a standard permutation corresponding to the permutation p.
EXAMPLES:
sage: import sage.combinat.permutation as permutation
sage: permutation.to_standard([4,2,7])
[2, 1, 3]
sage: permutation.to_standard([1,2,3])
[1, 2, 3]