Perfect matchings¶

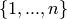A perfect matching of a set $S$ is a partition into 2-element sets. If $S$ is the set $\{1,...,n\}$ , it is equivalent to fixpoint-free involutions. These simple combinatorial objects appear in different domains such as combinatoric of orthogonal polynomials and of the hyperoctaedral groups (see [MV], [McD] and also [CM]):

AUTHOR:

Valentin Feray, 2010 : initial version

EXAMPLES:

Create a perfect matching:

sage: m=PerfectMatching([('a','e'),('b','c'),('d','f')]);m
PerfectMatching [('a', 'e'), ('b', 'c'), ('d', 'f')]

Count its crossings, if the ground set is totally ordered:

sage: n=PerfectMatching([3,8,1,7,6,5,4,2]); n
PerfectMatching [(1, 3), (2, 8), (4, 7), (5, 6)]
sage: n.number_of_crossings()
1

List the perfect matchings of a given ground set:

sage: PerfectMatchings(4).list()
[PerfectMatching [(4, 1), (3, 2)], PerfectMatching [(4, 2), (3, 1)], PerfectMatching [(4, 3), (2, 1)]]

REFERENCES:

[MV] combinatorics of orthogonal polynomials (A. de Medicis et X.Viennot, Moments des q-polynomes de Laguerre et la bijection de Foata-Zeilberger, Adv. Appl. Math., 15 (1994), 262-304)

[McD] combinatorics of hyperoctahedral group, double coset algebra and zonal polynomials (I. G. Macdonald, Symmetric functions and Hall polynomials, Oxford University Press, second edition, 1995, chapter VII).

[CM] (1, 2, 3) Benoit Collins, Sho Matsumoto, On some properties of orthogonal Weingarten functions, arXiv:0903.5143.

class sage.combinat.perfect_matching.PerfectMatching(value, parent)¶

Bases: sage.structure.element_wrapper.ElementWrapper

Class of perfect matching.

An instance of the class can be created from a list of pairs or from a fixed point-free involution as follows:

sage: m=PerfectMatching([('a','e'),('b','c'),('d','f')]);m
PerfectMatching [('a', 'e'), ('b', 'c'), ('d', 'f')]
sage: n=PerfectMatching([3,8,1,7,6,5,4,2]);n
PerfectMatching [(1, 3), (2, 8), (4, 7), (5, 6)]
sage: isinstance(m,PerfectMatching)
True

The parent, which is the set of perfect matching of the ground set, is automaticly created:

sage: n.parent()
Set of perfect matchings of {1, 2, 3, 4, 5, 6, 7, 8}

If the ground set is ordered, one can, for example, ask if the matching is non crossing:

sage: PerfectMatching([(1, 4), (2, 3), (5, 6)]).is_non_crossing()
True

TESTS:

sage: m=PerfectMatching([]); m
PerfectMatching []
sage: m.parent()
Set of perfect matchings of {}

Weingarten_function(d, other=None)¶

Returns the Weingarten function of two pairings.

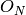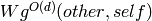This function is the value of some integrals over the orhtogonal groups $O_N$ . With the convention of [CM], the method returns $Wg^{O(d)}(other,self)$ .

EXAMPLES:

sage: var('N')
N
sage: m=PerfectMatching([(1,3),(2,4)])
sage: n=PerfectMatching([(1,2),(3,4)])
sage: factor(m.Weingarten_function(N,n))
-1/((N - 1)*(N + 2)*N)

conjugate_by_permutation(p)¶

Returns the conjugate of the perfect matching self by the permutation p of the ground set.

EXAMPLE:

sage: m=PerfectMatching([(1,4),(2,6),(3,5)])
sage: m.conjugate_by_permutation(Permutation([4,1,5,6,3,2]))
PerfectMatching [(4, 6), (1, 2), (5, 3)]

TEST:

sage: PerfectMatching([]).conjugate_by_permutation(Permutation([]))
PerfectMatching []

crossings()¶

INPUT:

A perfect matching on an totally ordered ground set.

OUTPUT:

We place the element of a ground set and draw the perfect matching by linking the elements of the same pair in the upper half-plane. This function returns the list of the pairs of crossing lines (as a line correspond to a pair, it returns a list of pairs of pairs).

EXAMPLES:

sage: n=PerfectMatching([3,8,1,7,6,5,4,2]); n
PerfectMatching [(1, 3), (2, 8), (4, 7), (5, 6)]
sage: n.crossings()
[((1, 3), (2, 8))]

TESTS:

sage: m=PerfectMatching([]); m.crossings()
[]

crossings_iterator()¶

INPUT:

A perfect matching on an totally ordered ground set.

OUTPUT:

We place the element of a ground set and draw the perfect matching by linking the elements of the same pair in the upper half-plane. This function returns an iterator over the pairs of crossing lines (as a line correspond to a pair, the iterator produces pairs of pairs).

EXAMPLES:

sage: n=PerfectMatching([3,8,1,7,6,5,4,2]); n
PerfectMatching [(1, 3), (2, 8), (4, 7), (5, 6)]
sage: it = n.crossings_iterator();
sage: it.next()
((1, 3), (2, 8))
sage: it.next()
...
StopIteration

is_non_crossing()¶

INPUT:

A perfect matching on an totally ordered ground set.

OUTPUT:

We place the element of a ground set and draw the perfect matching by linking the elements of the same pair in the upper half-plane. This function returns True if the picture obtained this way has no crossings.

EXAMPLES:

sage: n=PerfectMatching([3,8,1,7,6,5,4,2]); n
PerfectMatching [(1, 3), (2, 8), (4, 7), (5, 6)]
sage: n.is_non_crossing()
False
sage: PerfectMatching([(1, 4), (2, 3), (5, 6)]).is_non_crossing()
True

is_non_nesting()¶

INPUT:

A perfect matching on an totally ordered ground set.

OUTPUT:

We place the element of a ground set and draw the perfect matching by linking the elements of the same pair in the upper half-plane. This function returns True if the picture obtained this way has no nestings.

EXAMPLES:

sage: n=PerfectMatching([3,8,1,7,6,5,4,2]); n
PerfectMatching [(1, 3), (2, 8), (4, 7), (5, 6)]
sage: n.is_non_nesting()
False
sage: PerfectMatching([(1, 3), (2, 5), (4, 6)]).is_non_nesting()
True

loop_type(other=None)¶

INPUT:

other – a perfect matching of the same set of self. (if the second argument is empty, the method an_element() is called on the parent of the first)

OUTPUT:

If we draw the two perfect matchings simultaneously as edges of a graph, the graph obtained is a union of cycles of even lengths. The function returns the ordered list of the semi-length of these cycles (considered as a partition)

EXAMPLES:

sage: m=PerfectMatching([('a','e'),('b','c'),('d','f')])
sage: n=PerfectMatching([('a','b'),('d','f'),('e','c')])
sage: m.loop_type(n)
[2, 1]

TESTS:

sage: m=PerfectMatching([]); m.loop_type()
[]

loops(other=None)¶

INPUT:

other – a perfect matching of the same set of self. (if the second argument is empty, the method an_element() is called on the parent of the first)

OUTPUT:

If we draw the two perfect matchings simultaneously as edges of a graph, the graph obtained is a union of cycles of even lengths. The function returns the list of these cycles (each cycle is given as a list).

EXAMPLES:

sage: m=PerfectMatching([('a','e'),('b','c'),('d','f')])
sage: n=PerfectMatching([('a','b'),('d','f'),('e','c')])
sage: m.loops(n)
[['a', 'e', 'c', 'b'], ['d', 'f']]
sage: o=PerfectMatching([(1, 7), (2, 4), (3, 8), (5, 6)])
sage: p=PerfectMatching([(1, 6), (2, 7), (3, 4), (5, 8)])
sage: o.loops(p)
[[1, 7, 2, 4, 3, 8, 5, 6]]

loops_iterator(other=None)¶

INPUT:

other – a perfect matching of the same set of self. (if the second argument is empty, the method an_element() is called on the parent of the first)

OUTPUT:

If we draw the two perfect matchings simultaneously as edges of a graph, the graph obtained is a union of cycles of even lengths. The function returns an iterator for these cycles (each cycle is given as a list).

EXAMPLES:

sage: o=PerfectMatching([(1, 7), (2, 4), (3, 8), (5, 6)])
sage: p=PerfectMatching([(1, 6), (2, 7), (3, 4), (5, 8)])
sage: it=o.loops_iterator(p)
sage: it.next()
[1, 7, 2, 4, 3, 8, 5, 6]
sage: it.next()
...
StopIteration

nestings()¶

INPUT:

A perfect matching on an totally ordered ground set.

OUTPUT:

We place the element of a ground set and draw the perfect matching by linking the elements of the same pair in the upper half-plane. This function returns the list of the pairs of nesting lines (as a line correspond to a pair, it returns a list of pairs of pairs).

EXAMPLES:

sage: m=PerfectMatching([(1, 6), (2, 7), (3, 5), (4, 8)])
sage: m.nestings()
[((1, 6), (3, 5)), ((2, 7), (3, 5))]
sage: n=PerfectMatching([3,8,1,7,6,5,4,2]); n
PerfectMatching [(1, 3), (2, 8), (4, 7), (5, 6)]
sage: n.nestings()
[((2, 8), (4, 7)), ((2, 8), (5, 6)), ((4, 7), (5, 6))]

TESTS:

sage: m=PerfectMatching([]); m.nestings()
[]

nestings_iterator()¶

INPUT:

A perfect matching on an totally ordered ground set.

OUTPUT:

We place the element of a ground set and draw the perfect matching by linking the elements of the same pair in the upper half-plane. This function returns an iterator over the pairs of nesting lines (as a line correspond to a pair, the iterator produces pairs of pairs).

EXAMPLES:

sage: n=PerfectMatching([(1, 6), (2, 7), (3, 5), (4, 8)])
sage: it = n.nestings_iterator();
sage: it.next()
((1, 6), (3, 5))
sage: it.next()
((2, 7), (3, 5))
sage: it.next()
...
StopIteration

number_of_crossings()¶

INPUT:

A perfect matching on an totally ordered ground set.

OUTPUT:

We place the element of a ground set and draw the perfect matching by linking the elements of the same pair in the upper half-plane. This function returns the number the pairs of crossing lines.

EXAMPLES:

sage: n=PerfectMatching([3,8,1,7,6,5,4,2]); n
PerfectMatching [(1, 3), (2, 8), (4, 7), (5, 6)]
sage: n.number_of_crossings()
1

number_of_loops(other=None)¶

INPUT:

other – a perfect matching of the same set of self. (if the second argument is empty, the method an_element() is called on the parent of the first)

OUTPUT:

If we draw the two perfect matchings simultaneously as edges of a graph, the graph obtained is a union of cycles of even lengths. The function returns their numbers.

EXAMPLES:

sage: m=PerfectMatching([('a','e'),('b','c'),('d','f')])
sage: n=PerfectMatching([('a','b'),('d','f'),('e','c')])
sage: m.number_of_loops(n)
2

number_of_nestings()¶

INPUT:

A perfect matching on an totally ordered ground set.

OUTPUT:

We place the element of a ground set and draw the perfect matching by linking the elements of the same pair in the upper half-plane. This function returns the number the pairs of nesting lines.

EXAMPLES:

sage: n=PerfectMatching([3,8,1,7,6,5,4,2]); n
PerfectMatching [(1, 3), (2, 8), (4, 7), (5, 6)]
sage: n.number_of_nestings()
3

partner(x)¶

Returns the element in the same pair than x in the matching self.

EXAMPLES:

sage: m=PerfectMatching([(-3, 1), (2, 4), (-2, 7)]); m.partner(4)
2
sage: n=PerfectMatching([('c','b'),('d','f'),('e','a')])
sage: n.partner('c')
'b'

size()¶

Returns the size of the perfect matching self, i.e. the number of elements in the ground set.

EXAMPLES:

sage: m=PerfectMatching([(-3, 1), (2, 4), (-2, 7)]); m.size()
6

class sage.combinat.perfect_matching.PerfectMatchings(objects)¶

Bases: sage.structure.unique_representation.UniqueRepresentation, sage.structure.parent.Parent

Class of perfect matchings of a ground set. At the creation, the set can be given as any iterable object. If the argument is an integer $n$ , it will be transformed into $[1 .. n]$ :

sage: M=PerfectMatchings(6);M
Set of perfect matchings of {1, 2, 3, 4, 5, 6}
sage: PerfectMatchings([-1, -3, 1, 2])
Set of perfect matchings of {1, 2, -3, -1}

One can ask for the list, the cardinality or an element of a set of perfect matching:

sage: PerfectMatchings(4).list()
[PerfectMatching [(4, 1), (3, 2)], PerfectMatching [(4, 2), (3, 1)], PerfectMatching [(4, 3), (2, 1)]]
sage: PerfectMatchings(8).cardinality()
105
sage: M=PerfectMatchings(('a', 'e', 'b', 'f', 'c', 'd'))
sage: M.an_element()
PerfectMatching [('a', 'e'), ('c', 'd'), ('b', 'f')]
sage: all([PerfectMatchings(i).an_element() in PerfectMatchings(i)
...        for i in range(2,11,2)])
True

TESTS:

sage: PerfectMatchings(5).list()
[]
sage: TestSuite(PerfectMatchings(5)).run()
sage: TestSuite(PerfectMatchings([])).run()

Element¶: alias of PerfectMatching

Weingarten_matrix(*args, **kwds)¶

Returns the Weingarten matrix corresponding to the set of PerfectMatchings self. It is a useful theoretical tool to compute polynomial integral over the orthogonal group 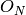$O_N$ (see [CM]).

EXAMPLES:

sage: M=PerfectMatchings(4).Weingarten_matrix(var('N'))
sage: N*(N-1)*(N+2)*M.apply_map(factor)
[N + 1    -1    -1]
[   -1 N + 1    -1]
[   -1    -1 N + 1]

an_element()¶

Returns an element of self.

EXAMPLES:

sage: M=PerfectMatchings(('a', 'e', 'b', 'f', 'c', 'd'))
sage: M.an_element()
PerfectMatching [('a', 'e'), ('c', 'd'), ('b', 'f')]
sage: all([PerfectMatchings(i).an_element() in PerfectMatchings(i)
...        for i in range(2,11,2)])
True

cardinality()¶

Returns the cardinality of the set of perfect matching self, that is 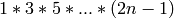$1*3*5*...*(2n-1)$ , where 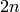$2n$ is the size of the ground set.

EXAMPLES:

sage: PerfectMatchings(8).cardinality()
105

Perfect matchings¶

Previous topic

Next topic

This Page

Navigation

Perfect matchings¶

Previous topic

Next topic

This Page

Quick search

Navigation