This library contains generic tools for constructing large sets whose elements can be enumerated by exploring a search space with a (lazy) tree or graph structure.
TODO:
Bases: object
A generic backtrack tool for exploring a search space organized as a tree, with branch pruning, etc.
See also SearchForest and TransitiveIdeal for handling simple special cases.
Bases: sage.combinat.combinat.CombinatorialClass
Returns the set of nodes of the forest having the given roots, and where children(x) returns the children of the node x of the forest.
See also GenericBacktracker, TransitiveIdeal, and TransitiveIdealGraded.
INPUT:
EXAMPLES:
A generator object for binary sequences of length 3, listed:
sage: list(SearchForest([[]], lambda l: [l+[0], l+[1]] if len(l) < 3 else []))
[[], [0], [0, 0], [0, 0, 0], [0, 0, 1], [0, 1], [0, 1, 0], [0, 1, 1], [1], [1, 0], [1, 0, 0], [1, 0, 1], [1, 1], [1, 1, 0], [1, 1, 1]]
A generator object for ordered sequences of length 2 from a 4-set, sampled:
sage: tb = SearchForest([[]], lambda l: [l + [i] for i in range(4) if i not in l] if len(l) < 2 else [])
sage: tb[0]
[]
sage: tb[16]
[3, 2]
Generic tool for constructing ideals of a relation.
INPUT:
Returns the set  of elements that can be obtained by repeated
application of relation on the elements of generators.
of elements that can be obtained by repeated
application of relation on the elements of generators.
Consider relation as modeling a directed graph (possibly with
loops, cycles, or circuits). Then  is the ideal generated by
generators under this relation.
is the ideal generated by
generators under this relation.
Enumerating the elements of  is achieved by depth first search
through the graph. The time complexity is
is achieved by depth first search
through the graph. The time complexity is 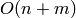 where
where  is
the size of the ideal, and
is
the size of the ideal, and 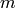 the number of edges in the
relation. The memory complexity is the depth, that is the maximal
distance between a generator and an element of
the number of edges in the
relation. The memory complexity is the depth, that is the maximal
distance between a generator and an element of  .
.
See also SearchForest and TransitiveIdealGraded.
EXAMPLES:
sage: [i for i in TransitiveIdeal(lambda i: [i+1] if i<10 else [], [0])]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
sage: [i for i in TransitiveIdeal(lambda i: [mod(i+1,3)], [0])]
[0, 1, 2]
sage: [i for i in TransitiveIdeal(lambda i: [mod(i+2,3)], [0])]
[0, 2, 1]
sage: [i for i in TransitiveIdeal(lambda i: [mod(i+2,10)], [0])]
[0, 2, 4, 6, 8]
sage: [i for i in TransitiveIdeal(lambda i: [mod(i+3,10),mod(i+5,10)], [0])]
[0, 3, 8, 1, 4, 5, 6, 7, 9, 2]
sage: [i for i in TransitiveIdeal(lambda i: [mod(i+4,10),mod(i+6,10)], [0])]
[0, 4, 8, 2, 6]
sage: [i for i in TransitiveIdeal(lambda i: [mod(i+3,9)], [0,1])]
[0, 1, 3, 4, 6, 7]
sage: [p for p in TransitiveIdeal(lambda x:[x],[Permutation([3,1,2,4]), Permutation([2,1,3,4])])]
[[2, 1, 3, 4], [3, 1, 2, 4]]
We now illustrate that the enumeration is done lazily, by depth first search:
sage: C = TransitiveIdeal(lambda x: [x-1, x+1], (-10, 0, 10))
sage: f = C.__iter__()
sage: [ f.next() for i in range(6) ]
[0, 1, 2, 3, 4, 5]
We compute all the permutations of 3:
sage: [p for p in TransitiveIdeal(attrcall("permutohedron_succ"), [Permutation([1,2,3])])]
[[1, 2, 3], [2, 1, 3], [1, 3, 2], [2, 3, 1], [3, 2, 1], [3, 1, 2]]
We compute all the permutations which are larger than [3,1,2,4], [2,1,3,4] in the right permutohedron:
sage: [p for p in TransitiveIdeal(attrcall("permutohedron_succ"), [Permutation([3,1,2,4]), Permutation([2,1,3,4])])]
[[2, 1, 3, 4], [2, 1, 4, 3], [2, 4, 1, 3], [4, 2, 1, 3], [4, 2, 3, 1], [4, 3, 2, 1], [3, 1, 2, 4], [2, 4, 3, 1], [3, 2, 1, 4], [2, 3, 1, 4], [2, 3, 4, 1], [3, 2, 4, 1], [3, 1, 4, 2], [3, 4, 2, 1], [3, 4, 1, 2], [4, 3, 1, 2]]
Bases: sage.combinat.backtrack.TransitiveIdeal
Generic tool for constructing ideals of a relation.
INPUT:
Returns the set  of elements that can be obtained by repeated
application of relation on the elements of generators.
of elements that can be obtained by repeated
application of relation on the elements of generators.
Consider relation as modeling a directed graph (possibly with
loops, cycles, or circuits). Then  is the ideal generated by
generators under this relation.
is the ideal generated by
generators under this relation.
Enumerating the elements of  is achieved by breath first search
through the graph; hence elements are enumerated by increasing
distance from the generators. The time complexity is
is achieved by breath first search
through the graph; hence elements are enumerated by increasing
distance from the generators. The time complexity is 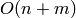 where
where  is the size of the ideal, and
is the size of the ideal, and 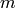 the number of edges in
the relation. The memory complexity is the depth, that is the
maximal distance between a generator and an element of
the number of edges in
the relation. The memory complexity is the depth, that is the
maximal distance between a generator and an element of  .
.
See also SearchForest and TransitiveIdeal.
EXAMPLES:
sage: [i for i in TransitiveIdealGraded(lambda i: [i+1] if i<10 else [], [0])]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
We now illustrates that the enumeration is done lazily, by breath first search:
sage: C = TransitiveIdealGraded(lambda x: [x-1, x+1], (-10, 0, 10))
sage: f = C.__iter__()
The elements at distance 0 from the generators:
sage: sorted([ f.next() for i in range(3) ])
[-10, 0, 10]
The elements at distance 1 from the generators:
sage: sorted([ f.next() for i in range(6) ])
[-11, -9, -1, 1, 9, 11]
The elements at distance 2 from the generators:
sage: sorted([ f.next() for i in range(6) ])
[-12, -8, -2, 2, 8, 12]
The enumeration order between elements at the same distance is not specified.
We compute all the permutations which are larger than [3,1,2,4] or [2,1,3,4] in the permutohedron:
sage: [p for p in TransitiveIdealGraded(attrcall("permutohedron_succ"), [Permutation([3,1,2,4]), Permutation([2,1,3,4])])]
[[3, 1, 2, 4], [2, 1, 3, 4], [2, 1, 4, 3], [3, 2, 1, 4], [2, 3, 1, 4], [3, 1, 4, 2], [2, 3, 4, 1], [3, 4, 1, 2], [3, 2, 4, 1], [2, 4, 1, 3], [2, 4, 3, 1], [4, 3, 1, 2], [4, 2, 1, 3], [3, 4, 2, 1], [4, 2, 3, 1], [4, 3, 2, 1]]
Returns an iterator on the nodes of the forest having the given roots, and where children(x) returns the children of the node x of the forest. Note that every node of the tree is returned, not simply the leaves.
INPUT:
EXAMPLES:
Search tree where leaves are binary sequences of length 3:
sage: from sage.combinat.backtrack import search_forest_iterator
sage: list(search_forest_iterator([[]], lambda l: [l+[0], l+[1]] if len(l) < 3 else []))
[[], [0], [0, 0], [0, 0, 0], [0, 0, 1], [0, 1], [0, 1, 0], [0, 1, 1], [1], [1, 0], [1, 0, 0], [1, 0, 1], [1, 1], [1, 1, 0], [1, 1, 1]]
Search tree where leaves are ordered sequences of length 2 from a 4-set:
sage: from sage.combinat.backtrack import search_forest_iterator
sage: list(search_forest_iterator([[]], lambda l: [l + [i] for i in range(4) if i not in l] if len(l) < 2 else []))
[[], [0], [0, 1], [0, 2], [0, 3], [1], [1, 0], [1, 2], [1, 3], [2], [2, 0], [2, 1], [2, 3], [3], [3, 0], [3, 1], [3, 2]]