Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Combinatorics »

A partition  of a nonnegative integer
of a nonnegative integer  is a
non-increasing list of positive integers (the parts of the
partition) with total sum
is a
non-increasing list of positive integers (the parts of the
partition) with total sum  .
.
A partition can be depicted by a diagram made of rows of cells,
where the number of cells in the 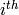 row starting from
the top is the
row starting from
the top is the 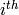 part of the partition.
part of the partition.
The coordinate system related to a partition applies from the top to the bottom and from left to right. So, the corners of the partition are [[0,4], [1,2], [2,0]].
AUTHORS:
EXAMPLES:
There are 5 partitions of the integer 4:
sage: Partitions(4).cardinality()
5
sage: Partitions(4).list()
[[4], [3, 1], [2, 2], [2, 1, 1], [1, 1, 1, 1]]
We can use the method .first() to get the ‘first’ partition of a number:
sage: Partitions(4).first()
[4]
Using the method .next(), we can calculate the ‘next’ partition. When we are at the last partition, None will be returned:
sage: Partitions(4).next([4])
[3, 1]
sage: Partitions(4).next([1,1,1,1]) is None
True
We can use iter to get an object which iterates over the partitions one by one to save memory. Note that when we do something like for part in Partitions(4) this iterator is used in the background:
sage: g = iter(Partitions(4))
sage: g.next()
[4]
sage: g.next()
[3, 1]
sage: g.next()
[2, 2]
sage: for p in Partitions(4): print p
[4]
[3, 1]
[2, 2]
[2, 1, 1]
[1, 1, 1, 1]
We can add constraints to to the type of partitions we want. For example, to get all of the partitions of 4 of length 2, we’d do the following:
sage: Partitions(4, length=2).list()
[[3, 1], [2, 2]]
Here is the list of partitions of length at least 2 and the list of ones with length at most 2:
sage: Partitions(4, min_length=2).list()
[[3, 1], [2, 2], [2, 1, 1], [1, 1, 1, 1]]
sage: Partitions(4, max_length=2).list()
[[4], [3, 1], [2, 2]]
The options min_part and max_part can be used to set constraints on the sizes of all parts. Using max_part, we can select partitions having only ‘small’ entries. The following is the list of the partitions of 4 with parts at most 2:
sage: Partitions(4, max_part=2).list()
[[2, 2], [2, 1, 1], [1, 1, 1, 1]]
The min_part options is complementary to max_part and selects partitions having only ‘large’ parts. Here is the list of all partitions of 4 with each part at least 2:
sage: Partitions(4, min_part=2).list()
[[4], [2, 2]]
The options inner and outer can be used to set part-by-part constraints. This is the list of partitions of 4 with [3, 1, 1] as an outer bound:
sage: Partitions(4, outer=[3,1,1]).list()
[[3, 1], [2, 1, 1]]
Outer sets max_length to the length of its argument. Moreover, the parts of outer may be infinite to clear constraints on specific parts. Here is the list of the partitions of 4 of length at most 3 such that the second and third part are 1 when they exist:
sage: Partitions(4, outer=[oo,1,1]).list()
[[4], [3, 1], [2, 1, 1]]
Finally, here are the partitions of 4 with [1,1,1] as an inner bound. Note that inner sets min_length to the length of its argument:
sage: Partitions(4, inner=[1,1,1]).list()
[[2, 1, 1], [1, 1, 1, 1]]
The options min_slope and max_slope can be used to set constraints on the slope, that is on the difference p[i+1]-p[i] of two consecutive parts. Here is the list of the strictly decreasing partitions of 4:
sage: Partitions(4, max_slope=-1).list()
[[4], [3, 1]]
The constraints can be combined together in all reasonable ways. Here are all the partitions of 11 of length between 2 and 4 such that the difference between two consecutive parts is between -3 and -1:
sage: Partitions(11,min_slope=-3,max_slope=-1,min_length=2,max_length=4).list()
[[7, 4], [6, 5], [6, 4, 1], [6, 3, 2], [5, 4, 2], [5, 3, 2, 1]]
Partition objects can also be created individually with the Partition function:
sage: Partition([2,1])
[2, 1]
Once we have a partition object, then there are a variety of methods that we can use. For example, we can get the conjugate of a partition. Geometrically, the conjugate of a partition is the reflection of that partition through its main diagonal. Of course, this operation is an involution:
sage: Partition([4,1]).conjugate()
[2, 1, 1, 1]
sage: Partition([4,1]).conjugate().conjugate()
[4, 1]
We can go back and forth between the exponential notations of a partition. The exponential notation can be padded with extra zeros:
sage: Partition([6,4,4,2,1]).to_exp()
[1, 1, 0, 2, 0, 1]
sage: Partition(exp=[1,1,0,2,0,1])
[6, 4, 4, 2, 1]
sage: Partition([6,4,4,2,1]).to_exp(5)
[1, 1, 0, 2, 0, 1]
sage: Partition([6,4,4,2,1]).to_exp(7)
[1, 1, 0, 2, 0, 1, 0]
sage: Partition([6,4,4,2,1]).to_exp(10)
[1, 1, 0, 2, 0, 1, 0, 0, 0, 0]
We can get the coordinates of the corners of a partition:
sage: Partition([4,3,1]).corners()
[(0, 3), (1, 2), (2, 0)]
We can compute the core and quotient of a partition and build the partition back up from them:
sage: Partition([6,3,2,2]).core(3)
[2, 1, 1]
sage: Partition([7,7,5,3,3,3,1]).quotient(3)
[[2], [1], [2, 2, 2]]
sage: p = Partition([11,5,5,3,2,2,2])
sage: p.core(3)
[]
sage: p.quotient(3)
[[2, 1], [4], [1, 1, 1]]
sage: Partition(core=[],quotient=[[2, 1], [4], [1, 1, 1]])
[11, 5, 5, 3, 2, 2, 2]
Returns the combinatorial class of ordered partitions of n. If k is specified, then only the ordered partitions of length k are returned.
Note
It is recommended that you use Compositions instead as OrderedPartitions wraps GAP. See also ordered_partitions.
EXAMPLES:
sage: OrderedPartitions(3)
Ordered partitions of 3
sage: OrderedPartitions(3).list()
[[3], [2, 1], [1, 2], [1, 1, 1]]
sage: OrderedPartitions(3,2)
Ordered partitions of 3 of length 2
sage: OrderedPartitions(3,2).list()
[[2, 1], [1, 2]]
Bases: sage.combinat.combinat.CombinatorialClass
EXAMPLES:
sage: OrderedPartitions(3).cardinality()
4
sage: OrderedPartitions(3,2).cardinality()
2
EXAMPLES:
sage: OrderedPartitions(3).list()
[[3], [2, 1], [1, 2], [1, 1, 1]]
sage: OrderedPartitions(3,2).list()
[[2, 1], [1, 2]]
A partition is a weakly decreasing ordered sequence of non-negative integers. This function returns a Sage partition object which can be specified in one of the following ways:
* a list (the default)
* using exponential notation
* by beta numbers (TODO)
* specifying the core and the quotient
* specifying the core and the canonical quotient (TODO)
See the examples below.
Sage follows the usual python conventions when dealing with partitions, so that the first part of the partition mu=Partition([4,3,2,2]) is mu[0], the second part is mu[1] and so on. As is usual, Sage ignores trailing zeros at the end of partitions.
EXAMPLES:
sage: Partition([3,2,1])
[3, 2, 1]
sage: Partition([3,2,1,0])
[3, 2, 1]
sage: Partition(exp=[2,1,1])
[3, 2, 1, 1]
sage: Partition(core=[2,1], quotient=[[2,1],[3],[1,1,1]])
[11, 5, 5, 3, 2, 2, 2]
sage: [2,1] in Partitions()
True
sage: [2,1,0] in Partitions()
False
sage: Partition([1,2,3])
...
ValueError: [1, 2, 3] is not a valid partition
Returns the combinatorial class of k-tuples of partitions of n. These are are ordered list of k partitions whose sizes add up to
TODO: reimplement in term of species.ProductSpecies and Partitions
These describe the classes and the characters of wreath products of
groups with k conjugacy classes with the symmetric group
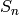 .
.
EXAMPLES:
sage: PartitionTuples(4,2)
2-tuples of partitions of 4
sage: PartitionTuples(3,2).list()
[[[3], []],
[[2, 1], []],
[[1, 1, 1], []],
[[2], [1]],
[[1, 1], [1]],
[[1], [2]],
[[1], [1, 1]],
[[], [3]],
[[], [2, 1]],
[[], [1, 1, 1]]]
Bases: sage.combinat.combinat.CombinatorialClass
Returns the number of k-tuples of partitions which together form a partition of n.
Wraps GAP’s NrPartitionTuples.
EXAMPLES:
sage: PartitionTuples(3,2).cardinality()
10
sage: PartitionTuples(8,2).cardinality()
185
Now we compare that with the result of the following GAP computation:
gap> S8:=Group((1,2,3,4,5,6,7,8),(1,2));
Group([ (1,2,3,4,5,6,7,8), (1,2) ])
gap> C2:=Group((1,2));
Group([ (1,2) ])
gap> W:=WreathProduct(C2,S8);
<permutation group of size 10321920 with 10 generators>
gap> Size(W);
10321920 ## = 2^8*Factorial(8), which is good:-)
gap> Size(ConjugacyClasses(W));
185
Bases: sage.combinat.combinat.CombinatorialObject
Returns a partition corresponding to self with a cell added in row i. i and j are 0-based row and column indices. This does not change p.
Note that if you have coordinates in a list, you can call this function with python’s * notation (see the examples below).
EXAMPLES:
sage: Partition([3, 2, 1, 1]).add_cell(0)
[4, 2, 1, 1]
sage: cell = [4, 0]; Partition([3, 2, 1, 1]).add_cell(*cell)
[3, 2, 1, 1, 1]
Returns a partition corresponding to self with a cell added in row i. i and j are 0-based row and column indices. This does not change p.
Note that if you have coordinates in a list, you can call this function with python’s * notation (see the examples below).
EXAMPLES:
sage: Partition([3, 2, 1, 1]).add_cell(0)
[4, 2, 1, 1]
sage: cell = [4, 0]; Partition([3, 2, 1, 1]).add_cell(*cell)
[3, 2, 1, 1, 1]
Returns a list of all the partitions that can be obtained by adding a horizontal border strip of length k to self.
EXAMPLES:
sage: Partition([]).add_horizontal_border_strip(0)
[[]]
sage: Partition([]).add_horizontal_border_strip(2)
[[2]]
sage: Partition([2,2]).add_horizontal_border_strip(2)
[[2, 2, 2], [3, 2, 1], [4, 2]]
sage: Partition([3,2,2]).add_horizontal_border_strip(2)
[[3, 2, 2, 2], [3, 3, 2, 1], [4, 2, 2, 1], [4, 3, 2], [5, 2, 2]]
TODO: reimplement like remove_horizontal_border_strip using IntegerListsLex
Returns a list of all the partitions that can be obtained by adding a vertical border strip of length k to self.
EXAMPLES:
sage: Partition([]).add_vertical_border_strip(0)
[[]]
sage: Partition([]).add_vertical_border_strip(2)
[[1, 1]]
sage: Partition([2,2]).add_vertical_border_strip(2)
[[3, 3], [3, 2, 1], [2, 2, 1, 1]]
sage: Partition([3,2,2]).add_vertical_border_strip(2)
[[4, 3, 2], [4, 2, 2, 1], [3, 3, 3], [3, 3, 2, 1], [3, 2, 2, 1, 1]]
Returns the length of the arm of cell (i,j) in partition p.
INPUT: i and j: two integers
OUPUT: an integer or a ValueError
The arm of cell (i,j) is the cells that appear to the right of cell (i,j). Note that i and j are 0-based indices. If your coordinates are in the form (i,j), use Python’s *-operator.
EXAMPLES:
sage: p = Partition([2,2,1])
sage: p.arm_length(0, 0)
1
sage: p.arm_length(0, 1)
0
sage: p.arm_length(2, 0)
0
sage: Partition([3,3]).arm_length(0, 0)
2
sage: Partition([3,3]).arm_length(*[0,0])
2
Returns the list of the cells of the arm of cell (i,j) in partition p.
INPUT: i and j: two integers
OUTPUT: a list of pairs of integers
The arm of cell (i,j) is the boxes that appear to the right of cell (i,j). Note that i and j are 0-based indices. If your coordinates are in the form (i,j), use Python’s *-operator.
Examples:
sage: Partition([4,4,3,1]).arm_cells(1,1)
[(1, 2), (1, 3)]
sage: Partition([]).arm_cells(0,0)
...
ValueError: The cells is not in the diagram
Returns the length of the arm of cell (i,j) in partition p.
INPUT: i and j: two integers
OUPUT: an integer or a ValueError
The arm of cell (i,j) is the cells that appear to the right of cell (i,j). Note that i and j are 0-based indices. If your coordinates are in the form (i,j), use Python’s *-operator.
EXAMPLES:
sage: p = Partition([2,2,1])
sage: p.arm_length(0, 0)
1
sage: p.arm_length(0, 1)
0
sage: p.arm_length(2, 0)
0
sage: Partition([3,3]).arm_length(0, 0)
2
sage: Partition([3,3]).arm_length(*[0,0])
2
Returns a tableau of shape p where each cell is filled its arm length. The optional boolean parameter flat provides the option of returning a flat list.
EXAMPLES:
sage: Partition([2,2,1]).arm_lengths()
[[1, 0], [1, 0], [0]]
sage: Partition([2,2,1]).arm_lengths(flat=True)
[1, 0, 1, 0, 0]
sage: Partition([3,3]).arm_lengths()
[[2, 1, 0], [2, 1, 0]]
sage: Partition([3,3]).arm_lengths(flat=True)
[2, 1, 0, 2, 1, 0]
This is a statistic on a cell c=(i,j) in the diagram of partition p given by
![[ (1 - q^{arm_length(c)} * t^{leg_length(c) + 1}) ] / [ (1 - q^{arm_length(c) + 1} * t^{leg_length(c)}) ]](../../_images/math/5230277606e17665d8da3f85a9324aba7fb36e91.png)
EXAMPLES:
sage: Partition([3,2,1]).arms_legs_coeff(1,1)
(-t + 1)/(-q + 1)
sage: Partition([3,2,1]).arms_legs_coeff(0,0)
(-q^2*t^3 + 1)/(-q^3*t^2 + 1)
sage: Partition([3,2,1]).arms_legs_coeff(*[0,0])
(-q^2*t^3 + 1)/(-q^3*t^2 + 1)
Returns the conjugate partition of the partition self. This is also called the associated partition in the literature.
EXAMPLES:
sage: Partition([2,2]).conjugate()
[2, 2]
sage: Partition([6,3,1]).conjugate()
[3, 2, 2, 1, 1, 1]
The conjugate partition is obtained by transposing the Ferrers diagram of the partition (see ferrers_diagram()):
sage: print Partition([6,3,1]).ferrers_diagram()
******
***
*
sage: print Partition([6,3,1]).conjugate().ferrers_diagram()
***
**
**
*
*
*
Returns a list of the standard tableaux of size self.size() whose atom is equal to self.
EXAMPLES:
sage: Partition([2,1]).atom()
[[[1, 2], [3]]]
sage: Partition([3,2,1]).atom()
[[[1, 2, 3, 6], [4, 5]], [[1, 2, 3], [4, 5], [6]]]
Returns a factor for the number of permutations with cycle type
self. self.aut() returns
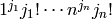 where
where 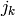 is the number of parts in self equal to k.
is the number of parts in self equal to k.
The number of permutations having  as a cycle type is
given by
as a cycle type is
given by
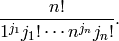
EXAMPLES:
sage: Partition([2,1]).aut()
2
Return the coordinates of the cells of self. Coordinates are given as (row-index, column-index) and are 0 based.
EXAMPLES:
sage: Partition([2,2]).cells()
[(0, 0), (0, 1), (1, 0), (1, 1)]
sage: Partition([3,2]).cells()
[(0, 0), (0, 1), (0, 2), (1, 0), (1, 1)]
Return the coordinates of the cells of self. Coordinates are given as (row-index, column-index) and are 0 based.
EXAMPLES:
sage: Partition([2,2]).cells()
[(0, 0), (0, 1), (1, 0), (1, 1)]
sage: Partition([3,2]).cells()
[(0, 0), (0, 1), (0, 2), (1, 0), (1, 1)]
Returns the size of the centralizer of any permutation of cycle type
self. If m_i is the multiplicity of i as a part of p, this is given
by ![\prod_i (i^m[i])*(m[i]!)](../../_images/math/88f5559420fc16a8700638976e231ee1f83532fa.png) . Including the optional
parameters t and q gives the q-t analog which is the former product
times
. Including the optional
parameters t and q gives the q-t analog which is the former product
times ![\prod_{i=1}^{length(p)} (1 - q^{p[i]}) / (1 - t^{p[i]}).](../../_images/math/266ad6b03bf536d5bff33d52b14c18bc41dc20e3.png)
EXAMPLES:
sage: Partition([2,2,1]).centralizer_size()
8
sage: Partition([2,2,2]).centralizer_size()
48
REFERENCES:
Returns the character polynomial associated to the partition self.
The character polynomial 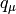 is defined by
is defined by
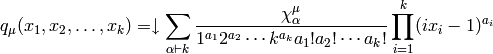
where 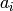 is the multiplicity of
is the multiplicity of  in
in
 .
.
It is computed in the following manner.
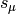 in the power-sum
basis.
in the power-sum
basis.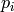 with
with 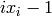
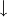 to the resulting
polynomial.
to the resulting
polynomial.EXAMPLES:
sage: Partition([1]).character_polynomial()
x - 1
sage: Partition([1,1]).character_polynomial()
1/2*x0^2 - 3/2*x0 - x1 + 1
sage: Partition([2,1]).character_polynomial()
1/3*x0^3 - 2*x0^2 + 8/3*x0 - x2
Returns the size of the conjugacy class of the symmetric group indexed by the partition p.
EXAMPLES:
sage: Partition([2,2,2]).conjugacy_class_size()
15
sage: Partition([2,2,1]).conjugacy_class_size()
15
sage: Partition([2,1,1]).conjugacy_class_size()
6
REFERENCES:
Returns the conjugate partition of the partition self. This is also called the associated partition in the literature.
EXAMPLES:
sage: Partition([2,2]).conjugate()
[2, 2]
sage: Partition([6,3,1]).conjugate()
[3, 2, 2, 1, 1, 1]
The conjugate partition is obtained by transposing the Ferrers diagram of the partition (see ferrers_diagram()):
sage: print Partition([6,3,1]).ferrers_diagram()
******
***
*
sage: print Partition([6,3,1]).conjugate().ferrers_diagram()
***
**
**
*
*
*
Returns True if p2 is a partition whose Ferrers diagram is contained in the Ferrers diagram of self
EXAMPLES:
sage: p = Partition([3,2,1])
sage: p.contains([2,1])
True
sage: all(p.contains(mu) for mu in Partitions(3))
True
sage: all(p.contains(mu) for mu in Partitions(4))
False
Returns the content statistic of the given cell, which is simply defined by j - i. This doesn’t technically depend on the partition, but is included here because it is often useful in the context of partitions.
EXAMPLES:
sage: Partition([2,1]).content(0,1)
1
sage: p = Partition([3,2])
sage: sum([p.content(*c) for c in p.cells()])
2
Returns the core of the partition – in the literature the core is
commonly referred to as the  -core,
-core,  -core,
-core,  -core, ... . The
construction of the core can be visualized by repeatedly removing
border strips of size
-core, ... . The
construction of the core can be visualized by repeatedly removing
border strips of size  from self until this is no longer possible.
The remaining partition is the core.
from self until this is no longer possible.
The remaining partition is the core.
EXAMPLES:
sage: Partition([6,3,2,2]).core(3)
[2, 1, 1]
sage: Partition([]).core(3)
[]
sage: Partition([8,7,7,4,1,1,1,1,1]).core(3)
[2, 1, 1]
TESTS:
sage: Partition([3,3,3,2,1]).core(3)
[]
sage: Partition([10,8,7,7]).core(4)
[]
sage: Partition([21,15,15,9,6,6,6,3,3]).core(3)
[]
Returns a list of the corners of the partitions. These are the positions where we can remove a cell. Indices are of the form (i,j) where i is the row-index and j is the column-index, and are 0-based.
EXAMPLES:
sage: Partition([3,2,1]).corners()
[(0, 2), (1, 1), (2, 0)]
sage: Partition([3,3,1]).corners()
[(1, 2), (2, 0)]
Returns a list of the partitions dominated by n. If n is specified, then it only returns the ones with = rows rows.
EXAMPLES:
sage: Partition([3,2,1]).dominate()
[[3, 2, 1], [3, 1, 1, 1], [2, 2, 2], [2, 2, 1, 1], [2, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1]]
sage: Partition([3,2,1]).dominate(rows=3)
[[3, 2, 1], [2, 2, 2]]
Returns True if partition p1 dominates partitions p2. Otherwise, it returns False.
EXAMPLES:
sage: p = Partition([3,2])
sage: p.dominates([3,1])
True
sage: p.dominates([2,2])
True
sage: p.dominates([2,1,1])
True
sage: p.dominates([3,3])
False
sage: p.dominates([4])
False
sage: Partition([4]).dominates(p)
False
sage: Partition([]).dominates([1])
False
sage: Partition([]).dominates([])
True
sage: Partition([1]).dominates([])
True
Returns a generator for partitions that can be obtained from p by removing a cell.
EXAMPLES:
sage: [p for p in Partition([2,1,1]).down()]
[[1, 1, 1], [2, 1]]
sage: [p for p in Partition([3,2]).down()]
[[2, 2], [3, 1]]
sage: [p for p in Partition([3,2,1]).down()]
[[2, 2, 1], [3, 1, 1], [3, 2]]
Returns a list of the partitions that can be obtained from the partition p by removing a cell.
EXAMPLES:
sage: Partition([2,1,1]).down_list()
[[1, 1, 1], [2, 1]]
sage: Partition([3,2]).down_list()
[[2, 2], [3, 1]]
sage: Partition([3,2,1]).down_list()
[[2, 2, 1], [3, 1, 1], [3, 2]]
Returns the evaluation of the partition.
EXAMPLES:
sage: Partition([4,3,1,1]).evaluation()
[2, 0, 1, 1]
Return the Ferrers diagram of pi.
INPUT:
EXAMPLES:
sage: print Partition([5,5,2,1]).ferrers_diagram()
*****
*****
**
*
Maps a  -bounded partition to a Grassmannian element in
the affine Weyl group of type
-bounded partition to a Grassmannian element in
the affine Weyl group of type  .
.
For details, see the documentation of the method from_kbounded_to_reduced_word() .
EXAMPLES:
sage: p=Partition([2,1,1])
sage: p.from_kbounded_to_grassmannian(2)
[-1 1 1]
[-2 2 1]
[-2 1 2]
sage: p=Partition([])
sage: p.from_kbounded_to_grassmannian(2)
[1 0 0]
[0 1 0]
[0 0 1]
Maps a  -bounded partition to a reduced word for an element in
the affine permutation group.
-bounded partition to a reduced word for an element in
the affine permutation group.
This uses the fact that there is a bijection between  -bounded partitions
and
-bounded partitions
and 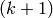 -cores and an action of the affine nilCoxeter algebra of type
-cores and an action of the affine nilCoxeter algebra of type
 on
on 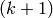 -cores as described in [LM2006].
-cores as described in [LM2006].
REFERENCES:
[LM2006] MR2167475 (2006j:05214) L. Lapointe, J. Morse. Tableaux on -cores, reduced words for affine permutations, and
-Schur expansions. J. Combin. Theory Ser. A 112 (2005), no. 1, 44–81.
EXAMPLES:
sage: p=Partition([2,1,1])
sage: p.from_kbounded_to_reduced_word(2)
[2, 1, 2, 0]
sage: p=Partition([3,1])
sage: p.from_kbounded_to_reduced_word(3)
[3, 2, 1, 0]
sage: p.from_kbounded_to_reduced_word(2)
...
ValueError: the partition must be 2-bounded
sage: p=Partition([])
sage: p.from_kbounded_to_reduced_word(2)
[]
Returns the generalized Pochhammer symbol
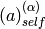 . This is the product over all
cells (i,j) in p of
. This is the product over all
cells (i,j) in p of 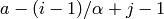 .
.
EXAMPLES:
sage: Partition([2,2]).generalized_pochhammer_symbol(2,1)
12
Returns the length of the hook of cell (i,j) in the partition p. The hook of cell (i,j) is defined as the cells to the right or below (in the English convention). Note that i and j are 0-based. If your coordinates are in the form (i,j), use Python’s *-operator.
EXAMPLES:
sage: p = Partition([2,2,1])
sage: p.hook_length(0, 0)
4
sage: p.hook_length(0, 1)
2
sage: p.hook_length(2, 0)
1
sage: Partition([3,3]).hook_length(0, 0)
4
sage: cell = [0,0]; Partition([3,3]).hook_length(*cell)
4
Returns the length of the hook of cell (i,j) in the partition p. The hook of cell (i,j) is defined as the cells to the right or below (in the English convention). Note that i and j are 0-based. If your coordinates are in the form (i,j), use Python’s *-operator.
EXAMPLES:
sage: p = Partition([2,2,1])
sage: p.hook_length(0, 0)
4
sage: p.hook_length(0, 1)
2
sage: p.hook_length(2, 0)
1
sage: Partition([3,3]).hook_length(0, 0)
4
sage: cell = [0,0]; Partition([3,3]).hook_length(*cell)
4
Returns a tableau of shape p with the cells filled in with the hook lengths.
In each cell, put the sum of one plus the number of cells horizontally to the right and vertically below the cell (the hook length).
For example, consider the partition [3,2,1] of 6 with Ferrers Diagram:
# # #
# #
#
When we fill in the cells with the hook lengths, we obtain:
5 3 1
3 1
1
EXAMPLES:
sage: Partition([2,2,1]).hook_lengths()
[[4, 2], [3, 1], [1]]
sage: Partition([3,3]).hook_lengths()
[[4, 3, 2], [3, 2, 1]]
sage: Partition([3,2,1]).hook_lengths()
[[5, 3, 1], [3, 1], [1]]
sage: Partition([2,2]).hook_lengths()
[[3, 2], [2, 1]]
sage: Partition([5]).hook_lengths()
[[5, 4, 3, 2, 1]]
REFERENCES:
Returns the two-variable hook polynomial.
EXAMPLES:
sage: R.<q,t> = PolynomialRing(QQ)
sage: a = Partition([2,2]).hook_polynomial(q,t)
sage: a == (1 - t)*(1 - q*t)*(1 - t^2)*(1 - q*t^2)
True
sage: a = Partition([3,2,1]).hook_polynomial(q,t)
sage: a == (1 - t)^3*(1 - q*t^2)^2*(1 - q^2*t^3)
True
Returns the Jack hook-product.
EXAMPLES:
sage: Partition([3,2,1]).hook_product(x)
(x + 2)^2*(2*x + 3)
sage: Partition([2,2]).hook_product(x)
2*(x + 1)*(x + 2)
Returns a sorted list of the hook lengths in self.
EXAMPLES:
sage: Partition([3,2,1]).hooks()
[5, 3, 3, 1, 1, 1]
EXAMPLES:
sage: part = Partition([3,2,1])
sage: jt = part.jacobi_trudi(); jt
[h[3] h[1] 0]
[h[4] h[2] h[]]
[h[5] h[3] h[1]]
sage: s = SFASchur(QQ)
sage: h = SFAHomogeneous(QQ)
sage: h( s(part) )
h[3, 2, 1] - h[3, 3] - h[4, 1, 1] + h[5, 1]
sage: jt.det()
h[3, 2, 1] - h[3, 3] - h[4, 1, 1] + h[5, 1]
EXAMPLES:
sage: p = Partition([3,2,1])
sage: p.k_atom(1)
[]
sage: p.k_atom(3)
[[[1, 1, 1], [2, 2], [3]],
[[1, 1, 1, 2], [2], [3]],
[[1, 1, 1, 3], [2, 2]],
[[1, 1, 1, 2, 3], [2]]]
sage: Partition([3,2,1]).k_atom(4)
[[[1, 1, 1], [2, 2], [3]], [[1, 1, 1, 3], [2, 2]]]
TESTS:
sage: Partition([1]).k_atom(1)
[[[1]]]
sage: Partition([1]).k_atom(2)
[[[1]]]
sage: Partition([]).k_atom(1)
[[]]
Returns the k-conjugate of the partition.
The k-conjugate is the partition that is given by the columns of the k-skew diagram of the partition.
EXAMPLES:
sage: p = Partition([4,3,2,2,1,1])
sage: p.k_conjugate(4)
[3, 2, 2, 1, 1, 1, 1, 1, 1]
Returns the k-skew partition.
The k-skew diagram of a k-bounded partition is the skew diagram
denoted 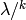 satisfying the conditions:
satisfying the conditions:
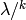 has length
has length 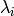
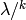 has hook-length exceeding k
has hook-length exceeding k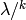 has hook
length exceeding k.
has hook
length exceeding k.REFERENCES:
EXAMPLES:
sage: p = Partition([4,3,2,2,1,1])
sage: p.k_skew(4)
[[9, 5, 3, 2, 1, 1], [5, 2, 1]]
Returns the k-split of self.
EXAMPLES:
sage: Partition([4,3,2,1]).k_split(3)
[]
sage: Partition([4,3,2,1]).k_split(4)
[[4], [3, 2], [1]]
sage: Partition([4,3,2,1]).k_split(5)
[[4, 3], [2, 1]]
sage: Partition([4,3,2,1]).k_split(6)
[[4, 3, 2], [1]]
sage: Partition([4,3,2,1]).k_split(7)
[[4, 3, 2, 1]]
sage: Partition([4,3,2,1]).k_split(8)
[[4, 3, 2, 1]]
Returns the length of the leg of cell (i,j) in partition p.
INPUT: i and j: two integers
OUPUT: an integer or a ValueError
The leg of cell (i,j) is defined to be the cells below it in partition p (in English convention). Note that i and j are 0-based. If your coordinates are in the form (i,j), use Python’s *-operator.
EXAMPLES:
sage: p = Partition([2,2,1])
sage: p.leg_length(0, 0)
2
sage: p.leg_length(0,1)
1
sage: p.leg_length(2,0)
0
sage: Partition([3,3]).leg_length(0, 0)
1
sage: cell = [0,0]; Partition([3,3]).leg_length(*cell)
1
Returns the list of the cells of the leg of cell (i,j) in partition p.
INPUT: i and j: two integers
OUTPUT: a list of pairs of integers
The leg of cell (i,j) is defined to be the cells below it in partition p (in English convention). Note that i and j are 0-based. If your coordinates are in the form (i,j), use Python’s *-operator.
Examples:
sage: Partition([4,4,3,1]).leg_cells(1,1)
[(2, 1)]
sage: Partition([4,4,3,1]).leg_cells(0,1)
[(1, 1), (2, 1)]
sage: Partition([]).leg_cells(0,0)
...
ValueError: The cells is not in the diagram
Returns the length of the leg of cell (i,j) in partition p.
INPUT: i and j: two integers
OUPUT: an integer or a ValueError
The leg of cell (i,j) is defined to be the cells below it in partition p (in English convention). Note that i and j are 0-based. If your coordinates are in the form (i,j), use Python’s *-operator.
EXAMPLES:
sage: p = Partition([2,2,1])
sage: p.leg_length(0, 0)
2
sage: p.leg_length(0,1)
1
sage: p.leg_length(2,0)
0
sage: Partition([3,3]).leg_length(0, 0)
1
sage: cell = [0,0]; Partition([3,3]).leg_length(*cell)
1
Returns a tableau of shape p with each cell filled in with its leg length. The optional boolean parameter flat provides the option of returning a flat list.
EXAMPLES:
sage: Partition([2,2,1]).leg_lengths()
[[2, 1], [1, 0], [0]]
sage: Partition([2,2,1]).leg_lengths(flat=True)
[2, 1, 1, 0, 0]
sage: Partition([3,3]).leg_lengths()
[[1, 1, 1], [0, 0, 0]]
sage: Partition([3,3]).leg_lengths(flat=True)
[1, 1, 1, 0, 0, 0]
Returns the number of parts in self.
EXAMPLES:
sage: Partition([3,2]).length()
2
sage: Partition([2,2,1]).length()
3
sage: Partition([]).length()
0
Returns the lower hook length of the cell (i,j) in self. When alpha == 1, this is just the normal hook length. Indices are 0-based.
The lower hook length of a cell (i,j) in a partition
 is defined by
is defined by
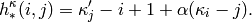
EXAMPLES:
sage: p = Partition([2,1])
sage: p.lower_hook(0,0,1)
3
sage: p.hook_length(0,0)
3
sage: [ p.lower_hook(i,j,x) for i,j in p.cells() ]
[x + 2, 1, 1]
Returns the lower hook lengths of the partition. When alpha == 1, these are just the normal hook lengths.
The lower hook length of a cell (i,j) in a partition
 is defined by
is defined by
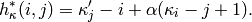
EXAMPLES:
sage: Partition([3,2,1]).lower_hook_lengths(x)
[[2*x + 3, x + 2, 1], [x + 2, 1], [1]]
sage: Partition([3,2,1]).lower_hook_lengths(1)
[[5, 3, 1], [3, 1], [1]]
sage: Partition([3,2,1]).hook_lengths()
[[5, 3, 1], [3, 1], [1]]
Returns the partition that lexicographically follows the partition p. If p is the last partition, then it returns False.
EXAMPLES:
sage: Partition([4]).next()
[3, 1]
sage: Partition([1,1,1,1]).next()
False
Returns the outer rim of self.
The outer rim of a partition  is defined as the cells which do not
belong to
is defined as the cells which do not
belong to  and which are adjacent to cells in
and which are adjacent to cells in  .
.
EXAMPLES:
The outer rim of the partition ![[4,1]](../../_images/math/3000cf1921f940e49588bcf054f7b35ce94f3266.png) consists of the cells marked
with # below:
consists of the cells marked
with # below:
****#
*####
##
sage: Partition([4,1]).outer_rim()
[(2, 0), (2, 1), (1, 1), (1, 2), (1, 3), (1, 4), (0, 4)]
sage: Partition([2,2,1]).outer_rim()
[(3, 0), (3, 1), (2, 1), (2, 2), (1, 2), (0, 2)]
sage: Partition([2,2]).outer_rim()
[(2, 0), (2, 1), (2, 2), (1, 2), (0, 2)]
sage: Partition([6,3,3,1,1]).outer_rim()
[(5, 0), (5, 1), (4, 1), (3, 1), (3, 2), (3, 3), (2, 3), (1, 3), (1, 4), (1, 5), (1, 6), (0, 6)]
sage: Partition([]).outer_rim()
[(0, 0)]
Returns a list of the positions where we can add a cell so that the shape is still a partition. Indices are of the form (i,j) where i is the row-index and j is the column-index, and are 0-based.
EXAMPLES:
sage: Partition([2,2,1]).outside_corners()
[(0, 2), (2, 1), (3, 0)]
sage: Partition([2,2]).outside_corners()
[(0, 2), (2, 0)]
sage: Partition([6,3,3,1,1,1]).outside_corners()
[(0, 6), (1, 3), (3, 1), (6, 0)]
sage: Partition([]).outside_corners()
[(0, 0)]
Returns the combinatorial class of partitions of sum(self).
EXAMPLES:
sage: Partition([3,2,1]).parent()
Partitions of the integer 6
Returns the cycle type of the  -th power of any permutation
with cycle type self (thus describes the powermap of
symmetric groups).
-th power of any permutation
with cycle type self (thus describes the powermap of
symmetric groups).
Wraps GAP’s PowerPartition.
EXAMPLES:
sage: p = Partition([5,3])
sage: p.power(1)
[5, 3]
sage: p.power(2)
[5, 3]
sage: p.power(3)
[5, 1, 1, 1]
sage: p.power(4)
[5, 3]
sage: Partition([3,2,1]).power(3)
[2, 1, 1, 1, 1]
Now let us compare this to the power map on 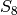 :
:
sage: G = SymmetricGroup(8)
sage: g = G([(1,2,3,4,5),(6,7,8)])
sage: g
(1,2,3,4,5)(6,7,8)
sage: g^2
(1,3,5,2,4)(6,8,7)
sage: g^3
(1,4,2,5,3)
sage: g^4
(1,5,4,3,2)(6,7,8)
EXAMPLES:
sage: Partition([5,5,2,1]).pp()
*****
*****
**
*
Returns the quotient of the partition – in the literature the
core is commonly referred to as the  -core,
-core,  -core,
-core,  -core, ... . The
quotient is a list of
-core, ... . The
quotient is a list of  partitions, constructed in the following
way. Label each cell in
partitions, constructed in the following
way. Label each cell in  with its content, modulo
with its content, modulo  . Let
. Let 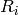 be
the set of rows ending in a cell labelled
be
the set of rows ending in a cell labelled  , and
, and 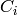 be the set of
columns ending in a cell labelled
be the set of
columns ending in a cell labelled  . Then the
. Then the  -th component of the
quotient of
-th component of the
quotient of  is the partition defined by intersecting
is the partition defined by intersecting 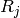 with
with
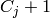 .
.
EXAMPLES:
sage: Partition([7,7,5,3,3,3,1]).quotient(3)
[[2], [1], [2, 2, 2]]
TESTS:
sage: Partition([8,7,7,4,1,1,1,1,1]).quotient(3)
[[2, 1], [2, 2], [2]]
sage: Partition([10,8,7,7]).quotient(4)
[[2], [3], [2], [1]]
sage: Partition([6,3,3]).quotient(3)
[[1], [1], [2]]
sage: Partition([3,3,3,2,1]).quotient(3)
[[1], [1, 1], [1]]
sage: Partition([6,6,6,3,3,3]).quotient(3)
[[2, 1], [2, 1], [2, 1]]
sage: Partition([21,15,15,9,6,6,6,3,3]).quotient(3)
[[5, 2, 1], [5, 2, 1], [7, 3, 2]]
sage: Partition([21,15,15,9,6,6,3,3]).quotient(3)
[[5, 2], [5, 2, 1], [7, 3, 1]]
sage: Partition([14,12,11,10,10,10,10,9,6,4,3,3,2,1]).quotient(5)
[[3, 3], [2, 2, 1], [], [3, 3, 3], [1]]
Returns the core of the partition – in the literature the core is
commonly referred to as the  -core,
-core,  -core,
-core,  -core, ... . The
construction of the core can be visualized by repeatedly removing
border strips of size
-core, ... . The
construction of the core can be visualized by repeatedly removing
border strips of size  from self until this is no longer possible.
The remaining partition is the core.
from self until this is no longer possible.
The remaining partition is the core.
EXAMPLES:
sage: Partition([6,3,2,2]).core(3)
[2, 1, 1]
sage: Partition([]).core(3)
[]
sage: Partition([8,7,7,4,1,1,1,1,1]).core(3)
[2, 1, 1]
TESTS:
sage: Partition([3,3,3,2,1]).core(3)
[]
sage: Partition([10,8,7,7]).core(4)
[]
sage: Partition([21,15,15,9,6,6,6,3,3]).core(3)
[]
Returns the quotient of the partition – in the literature the
core is commonly referred to as the  -core,
-core,  -core,
-core,  -core, ... . The
quotient is a list of
-core, ... . The
quotient is a list of  partitions, constructed in the following
way. Label each cell in
partitions, constructed in the following
way. Label each cell in  with its content, modulo
with its content, modulo  . Let
. Let 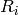 be
the set of rows ending in a cell labelled
be
the set of rows ending in a cell labelled  , and
, and 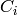 be the set of
columns ending in a cell labelled
be the set of
columns ending in a cell labelled  . Then the
. Then the  -th component of the
quotient of
-th component of the
quotient of  is the partition defined by intersecting
is the partition defined by intersecting 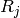 with
with
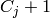 .
.
EXAMPLES:
sage: Partition([7,7,5,3,3,3,1]).quotient(3)
[[2], [1], [2, 2, 2]]
TESTS:
sage: Partition([8,7,7,4,1,1,1,1,1]).quotient(3)
[[2, 1], [2, 2], [2]]
sage: Partition([10,8,7,7]).quotient(4)
[[2], [3], [2], [1]]
sage: Partition([6,3,3]).quotient(3)
[[1], [1], [2]]
sage: Partition([3,3,3,2,1]).quotient(3)
[[1], [1, 1], [1]]
sage: Partition([6,6,6,3,3,3]).quotient(3)
[[2, 1], [2, 1], [2, 1]]
sage: Partition([21,15,15,9,6,6,6,3,3]).quotient(3)
[[5, 2, 1], [5, 2, 1], [7, 3, 2]]
sage: Partition([21,15,15,9,6,6,3,3]).quotient(3)
[[5, 2], [5, 2, 1], [7, 3, 1]]
sage: Partition([14,12,11,10,10,10,10,9,6,4,3,3,2,1]).quotient(5)
[[3, 3], [2, 2, 1], [], [3, 3, 3], [1]]
EXAMPLES:
sage: Partition([3,2,1]).reading_tableau()
[[1, 3, 6], [2, 5], [4]]
Returns the partition obtained by removing a cell at the end of row i.
EXAMPLES:
sage: Partition([2,2]).remove_cell(1)
[2, 1]
sage: Partition([2,2,1]).remove_cell(2)
[2, 2]
sage: #Partition([2,2]).remove_cell(0)
sage: Partition([2,2]).remove_cell(1,1)
[2, 1]
sage: #Partition([2,2]).remove_cell(1,0)
Returns the partition obtained by removing a cell at the end of row i.
EXAMPLES:
sage: Partition([2,2]).remove_cell(1)
[2, 1]
sage: Partition([2,2,1]).remove_cell(2)
[2, 2]
sage: #Partition([2,2]).remove_cell(0)
sage: Partition([2,2]).remove_cell(1,1)
[2, 1]
sage: #Partition([2,2]).remove_cell(1,0)
Returns the partitions obtained from self by removing an horizontal border strip of length k
EXAMPLES:
sage: Partition([5,3,1]).remove_horizontal_border_strip(0).list()
[[5, 3, 1]]
sage: Partition([5,3,1]).remove_horizontal_border_strip(1).list()
[[5, 3], [5, 2, 1], [4, 3, 1]]
sage: Partition([5,3,1]).remove_horizontal_border_strip(2).list()
[[5, 2], [5, 1, 1], [4, 3], [4, 2, 1], [3, 3, 1]]
sage: Partition([5,3,1]).remove_horizontal_border_strip(3).list()
[[5, 1], [4, 2], [4, 1, 1], [3, 3], [3, 2, 1]]
sage: Partition([5,3,1]).remove_horizontal_border_strip(4).list()
[[4, 1], [3, 2], [3, 1, 1]]
sage: Partition([5,3,1]).remove_horizontal_border_strip(5).list()
[[3, 1]]
sage: Partition([5,3,1]).remove_horizontal_border_strip(6).list()
[]
The result is returned as a combinatorial class:
sage: Partition([5,3,1]).remove_horizontal_border_strip(5)
The subpartitions of [5, 3, 1] obtained by removing an horizontal border strip of length 5
TESTS:
sage: Partition([3,2,2]).remove_horizontal_border_strip(2).list()
[[3, 2], [2, 2, 1]]
sage: Partition([3,2,2]).remove_horizontal_border_strip(2).first().parent()
Partitions...
sage: Partition([]).remove_horizontal_border_strip(0).list()
[[]]
sage: Partition([]).remove_horizontal_border_strip(6).list()
[]
Returns the rim of self.
The rim of a partition  is defined as the cells which belong to
is defined as the cells which belong to
 and which are adjacent to cells not in
and which are adjacent to cells not in  .
.
EXAMPLES:
The rim of the partition ![[5,5,2,1]](../../_images/math/7c65717cd8b55473d638d22d2ad3b1526a874c4b.png) consists of the cells marked with
# below:
consists of the cells marked with
# below:
****#
*####
##
#
sage: Partition([5,5,2,1]).rim()
[(3, 0), (2, 0), (2, 1), (1, 1), (1, 2), (1, 3), (1, 4), (0, 4)]
sage: Partition([2,2,1]).rim()
[(2, 0), (1, 0), (1, 1), (0, 1)]
sage: Partition([2,2]).rim()
[(1, 0), (1, 1), (0, 1)]
sage: Partition([6,3,3,1,1]).rim()
[(4, 0), (3, 0), (2, 0), (2, 1), (2, 2), (1, 2), (0, 2), (0, 3), (0, 4), (0, 5)]
sage: Partition([]).rim()
[]
Returns the sign of any permutation with cycle type self.
This function corresponds to a homomorphism from the symmetric
group 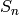 into the cyclic group of order 2, whose kernel
is exactly the alternating group
into the cyclic group of order 2, whose kernel
is exactly the alternating group 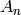 . Partitions of sign
. Partitions of sign
 are called even partitions while partitions of sign
are called even partitions while partitions of sign
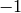 are called odd.
are called odd.
EXAMPLES:
sage: Partition([5,3]).sign()
1
sage: Partition([5,2]).sign()
-1
Zolotarev’s lemma states that the Legendre symbol
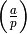 for an integer
for an integer
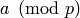 (
( a prime number), can be computed
as sign(p_a), where sign denotes the sign of a permutation and
p_a the permutation of the residue classes
a prime number), can be computed
as sign(p_a), where sign denotes the sign of a permutation and
p_a the permutation of the residue classes  induced by modular multiplication by
induced by modular multiplication by  , provided
, provided
 does not divide
does not divide  .
.
We verify this in some examples.
sage: F = GF(11)
sage: a = F.multiplicative_generator();a
2
sage: plist = [int(a*F(x)) for x in range(1,11)]; plist
[2, 4, 6, 8, 10, 1, 3, 5, 7, 9]
This corresponds to the permutation (1, 2, 4, 8, 5, 10, 9, 7, 3, 6)
(acting the set 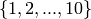 ) and to the partition
[10].
) and to the partition
[10].
sage: p = PermutationGroupElement('(1, 2, 4, 8, 5, 10, 9, 7, 3, 6)')
sage: p.sign()
-1
sage: Partition([10]).sign()
-1
sage: kronecker_symbol(11,2)
-1
Now replace  by
by 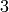 :
:
sage: plist = [int(F(3*x)) for x in range(1,11)]; plist
[3, 6, 9, 1, 4, 7, 10, 2, 5, 8]
sage: range(1,11)
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
sage: p = PermutationGroupElement('(3,4,8,7,9)')
sage: p.sign()
1
sage: kronecker_symbol(3,11)
1
sage: Partition([5,1,1,1,1,1]).sign()
1
In both cases, Zolotarev holds.
REFERENCES:
Returns the size of partition p.
EXAMPLES:
sage: Partition([2,2]).size()
4
sage: Partition([3,2,1]).size()
6
Return a list of the multiplicities of the parts of a partition. Use the optional parameter k to get a return list of length at least k.
EXAMPLES:
sage: Partition([3,2,2,1]).to_exp()
[1, 2, 1]
sage: Partition([3,2,2,1]).to_exp(5)
[1, 2, 1, 0, 0]
Returns a dictionary containing the multiplicities of the parts of this partition.
EXAMPLES:
sage: p = Partition([4,2,2,1])
sage: d = p.to_exp_dict()
sage: d[4]
1
sage: d[2]
2
sage: d[1]
1
sage: 5 in d
False
Return self as a list.
EXAMPLES:
sage: p = Partition([2,1]).to_list(); p
[2, 1]
sage: type(p)
<type 'list'>
TESTS:
sage: p = Partition([2,1])
sage: pl = p.to_list()
sage: pl[0] = 0; p
[2, 1]
Returns a generator for partitions that can be obtained from pi by adding a cell.
EXAMPLES:
sage: [p for p in Partition([2,1,1]).up()]
[[3, 1, 1], [2, 2, 1], [2, 1, 1, 1]]
sage: [p for p in Partition([3,2]).up()]
[[4, 2], [3, 3], [3, 2, 1]]
Returns a list of the partitions that can be formed from the partition p by adding a cell.
EXAMPLES:
sage: Partition([2,1,1]).up_list()
[[3, 1, 1], [2, 2, 1], [2, 1, 1, 1]]
sage: Partition([3,2]).up_list()
[[4, 2], [3, 3], [3, 2, 1]]
Returns the upper hook length of the cell (i,j) in self. When alpha == 1, this is just the normal hook length. As usual, indices are 0 based.
The upper hook length of a cell (i,j) in a partition
 is defined by
is defined by
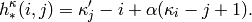
EXAMPLES:
sage: p = Partition([2,1])
sage: p.upper_hook(0,0,1)
3
sage: p.hook_length(0,0)
3
sage: [ p.upper_hook(i,j,x) for i,j in p.cells() ]
[2*x + 1, x, x]
Returns the upper hook lengths of the partition. When alpha == 1, these are just the normal hook lengths.
The upper hook length of a cell (i,j) in a partition
 is defined by
is defined by
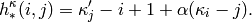
EXAMPLES:
sage: Partition([3,2,1]).upper_hook_lengths(x)
[[3*x + 2, 2*x + 1, x], [2*x + 1, x], [x]]
sage: Partition([3,2,1]).upper_hook_lengths(1)
[[5, 3, 1], [3, 1], [1]]
sage: Partition([3,2,1]).hook_lengths()
[[5, 3, 1], [3, 1], [1]]
Returns sum([i*p[i] for i in range(len(p))]). It is also the sum of the leg length of every cell in b, or the sum of binomial(s[i],2) for s the conjugate partition of p.
EXAMPLES:
sage: Partition([2,2]).weighted_size()
2
sage: Partition([3,3,3]).weighted_size()
9
sage: Partition([5,2]).weighted_size()
2
Partitions(n, **kwargs) returns the combinatorial class of
integer partitions of  , subject to the constraints given by the
keywords.
, subject to the constraints given by the
keywords.
Valid keywords are: starting, ending, min_part, max_part, max_length, min_length, length, max_slope, min_slope, inner, outer, and parts_in. They have the following meanings:
 in reverse lex order.
in reverse lex order. parts.
parts. parts.
parts. .
. .
. ; the slope is the difference between successive parts.
; the slope is the difference between successive parts. , which can be any sequence of positive integers.
, which can be any sequence of positive integers.The max_* versions, along with inner and ending, work analogously.
Right now, the parts_in, starting, and ending keyword arguments are mutually exclusive, both of each other and of other keyword arguments. If you specify, say, parts_in, all other keyword arguments will be ignored; starting and ending work the same way.
EXAMPLES: If no arguments are passed, then the combinatorial class of all integer partitions is returned.
sage: Partitions()
Partitions
sage: [2,1] in Partitions()
True
If an integer  is passed, then the combinatorial class of integer
partitions of
is passed, then the combinatorial class of integer
partitions of  is returned.
is returned.
sage: Partitions(3)
Partitions of the integer 3
sage: Partitions(3).list()
[[3], [2, 1], [1, 1, 1]]
If starting=p is passed, then the combinatorial class of partitions
greater than or equal to  in lexicographic order is returned.
in lexicographic order is returned.
sage: Partitions(3, starting=[2,1])
Partitions of the integer 3 starting with [2, 1]
sage: Partitions(3, starting=[2,1]).list()
[[2, 1], [1, 1, 1]]
If ending=p is passed, then the combinatorial class of
partitions at most  in lexicographic order is returned.
in lexicographic order is returned.
sage: Partitions(3, ending=[2,1])
Partitions of the integer 3 ending with [2, 1]
sage: Partitions(3, ending=[2,1]).list()
[[3], [2, 1]]
Using max_slope=-1 yields partitions into distinct parts – each part differs from the next by at least 1. Use a different max_slope to get parts that differ by, say, 2.
sage: Partitions(7, max_slope=-1).list()
[[7], [6, 1], [5, 2], [4, 3], [4, 2, 1]]
sage: Partitions(15, max_slope=-1).cardinality()
27
The number of partitions of  into odd parts equals the number of
partitions into distinct parts. Let’s test that for
into odd parts equals the number of
partitions into distinct parts. Let’s test that for  from 10 to 20.
from 10 to 20.
sage: test = lambda n: Partitions(n, max_slope=-1).cardinality() == Partitions(n, parts_in=[1,3..n]).cardinality()
sage: all(test(n) for n in [10..20])
True
The number of partitions of  into distinct parts that differ by
at least 2 equals the number of partitions into parts that equal 1
or 4 modulo 5; this is one of the Rogers-Ramanujan identities.
into distinct parts that differ by
at least 2 equals the number of partitions into parts that equal 1
or 4 modulo 5; this is one of the Rogers-Ramanujan identities.
sage: test = lambda n: Partitions(n, max_slope=-2).cardinality() == Partitions(n, parts_in=([1,6..n] + [4,9..n])).cardinality()
sage: all(test(n) for n in [10..20])
True
Here are some more examples illustrating min_part, max_part, and length.
sage: Partitions(5,min_part=2)
Partitions of the integer 5 satisfying constraints min_part=2
sage: Partitions(5,min_part=2).list()
[[5], [3, 2]]
sage: Partitions(3,max_length=2).list()
[[3], [2, 1]]
sage: Partitions(10, min_part=2, length=3).list()
[[6, 2, 2], [5, 3, 2], [4, 4, 2], [4, 3, 3]]
Here are some further examples using various constraints:
sage: [x for x in Partitions(4)]
[[4], [3, 1], [2, 2], [2, 1, 1], [1, 1, 1, 1]]
sage: [x for x in Partitions(4, length=2)]
[[3, 1], [2, 2]]
sage: [x for x in Partitions(4, min_length=2)]
[[3, 1], [2, 2], [2, 1, 1], [1, 1, 1, 1]]
sage: [x for x in Partitions(4, max_length=2)]
[[4], [3, 1], [2, 2]]
sage: [x for x in Partitions(4, min_length=2, max_length=2)]
[[3, 1], [2, 2]]
sage: [x for x in Partitions(4, max_part=2)]
[[2, 2], [2, 1, 1], [1, 1, 1, 1]]
sage: [x for x in Partitions(4, min_part=2)]
[[4], [2, 2]]
sage: [x for x in Partitions(4, outer=[3,1,1])]
[[3, 1], [2, 1, 1]]
sage: [x for x in Partitions(4, outer=[infinity, 1, 1])]
[[4], [3, 1], [2, 1, 1]]
sage: [x for x in Partitions(4, inner=[1,1,1])]
[[2, 1, 1], [1, 1, 1, 1]]
sage: [x for x in Partitions(4, max_slope=-1)]
[[4], [3, 1]]
sage: [x for x in Partitions(4, min_slope=-1)]
[[4], [2, 2], [2, 1, 1], [1, 1, 1, 1]]
sage: [x for x in Partitions(11, max_slope=-1, min_slope=-3, min_length=2, max_length=4)]
[[7, 4], [6, 5], [6, 4, 1], [6, 3, 2], [5, 4, 2], [5, 3, 2, 1]]
sage: [x for x in Partitions(11, max_slope=-1, min_slope=-3, min_length=2, max_length=4, outer=[6,5,2])]
[[6, 5], [6, 4, 1], [6, 3, 2], [5, 4, 2]]
Note that if you specify min_part=0, then the objects produced will have parts equal to zero which violates some internal assumptions that the Partition class makes.
sage: [x for x in Partitions(4, length=3, min_part=0)]
doctest:... RuntimeWarning: Currently, setting min_part=0 produces Partition objects which violate internal assumptions. Calling methods on these objects may produce errors or WRONG results!
[[4, 0, 0], [3, 1, 0], [2, 2, 0], [2, 1, 1]]
sage: [x for x in Partitions(4, min_length=3, min_part=0)]
[[4, 0, 0], [3, 1, 0], [2, 2, 0], [2, 1, 1], [1, 1, 1, 1]]
Except for very special cases, counting is done by brute force iteration through all the partitions. However the iteration itself has a reasonable complexity (constant memory, constant amortized time), which allow for manipulating large partitions:
sage: Partitions(1000, max_length=1).list()
[[1000]]
In particular, getting the first element is also constant time:
sage: Partitions(30, max_part=29).first()
[29, 1]
TESTS:
sage: P = Partitions(5, min_part=2)
sage: P == loads(dumps(P))
True
sage: repr( Partitions(5, min_part=2) )
'Partitions of the integer 5 satisfying constraints min_part=2'
sage: P = Partitions(5, min_part=2)
sage: P.first().parent()
Partitions...
sage: [2,1] in P
False
sage: [2,2,1] in P
False
sage: [3,2] in P
True
Bases: sage.combinat.integer_list.IntegerListsLex
Returns combinatorial class of all (unordered) “restricted” partitions of the integer n having its greatest part equal to the integer k.
EXAMPLES:
sage: PartitionsGreatestEQ(10,2)
Partitions of 10 having greatest part equal to 2
sage: PartitionsGreatestEQ(10,2).list()
[[2, 2, 2, 2, 2],
[2, 2, 2, 2, 1, 1],
[2, 2, 2, 1, 1, 1, 1],
[2, 2, 1, 1, 1, 1, 1, 1],
[2, 1, 1, 1, 1, 1, 1, 1, 1]]
sage: [4,3,2,1] in PartitionsGreatestEQ(10,2)
False
sage: [2,2,2,2,2] in PartitionsGreatestEQ(10,2)
True
sage: [1]*10 in PartitionsGreatestEQ(10,2)
False
sage: PartitionsGreatestEQ(10,2).first().parent()
Partitions...
TESTS:
sage: p = PartitionsGreatestEQ(10,2)
sage: p == loads(dumps(p))
True
Bases: sage.combinat.integer_list.IntegerListsLex
Returns the combinatorial class of all (unordered) “restricted” partitions of the integer n having parts less than or equal to the integer k.
EXAMPLES:
sage: PartitionsGreatestLE(10,2)
Partitions of 10 having parts less than or equal to 2
sage: PartitionsGreatestLE(10,2).list()
[[2, 2, 2, 2, 2],
[2, 2, 2, 2, 1, 1],
[2, 2, 2, 1, 1, 1, 1],
[2, 2, 1, 1, 1, 1, 1, 1],
[2, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1]]
sage: [4,3,2,1] in PartitionsGreatestLE(10,2)
False
sage: [2,2,2,2,2] in PartitionsGreatestLE(10,2)
True
sage: PartitionsGreatestLE(10,2).first().parent()
Partitions...
TESTS:
sage: p = PartitionsGreatestLE(10,2)
sage: p == loads(dumps(p))
True
Returns the combinatorial class of partitions that fit in a h by w box.
EXAMPLES:
sage: PartitionsInBox(2,2)
Integer partitions which fit in a 2 x 2 box
sage: PartitionsInBox(2,2).list()
[[], [1], [1, 1], [2], [2, 1], [2, 2]]
Bases: sage.combinat.combinat.CombinatorialClass
Returns a list of all the partitions inside a box of height h and width w.
EXAMPLES:
sage: PartitionsInBox(2,2).list()
[[], [1], [1, 1], [2], [2, 1], [2, 2]]
Bases: sage.combinat.combinat.InfiniteAbstractCombinatorialClass
Returns the number of integer partitions.
EXAMPLES:
sage: Partitions().cardinality()
+Infinity
Bases: sage.combinat.combinat.CombinatorialClass
EXAMPLES:
sage: Partitions(4, ending=[1,1,1,1]).first()
[4]
EXAMPLES:
sage: Partitions(4, ending=[1,1,1,1]).next(Partition([4]))
[3, 1]
sage: Partitions(4, ending=[1,1,1,1]).next(Partition([1,1,1,1])) is None
True
Bases: sage.combinat.combinat.CombinatorialClass
INPUT:
 is in the thousands, in which case PARI is
faster. But PARI has a bug, e.g., on 64-bit Linux
PARI-2.3.2 outputs numbpart(147007)%1000 as 536, but it
should be 533!. So do not use this option.
is in the thousands, in which case PARI is
faster. But PARI has a bug, e.g., on 64-bit Linux
PARI-2.3.2 outputs numbpart(147007)%1000 as 536, but it
should be 533!. So do not use this option.Use the function partitions(n) to return a
generator over all partitions of  .
.
It is possible to associate with every partition of the integer n a conjugacy class of permutations in the symmetric group on n points and vice versa. Therefore p(n) = NrPartitions(n) is the number of conjugacy classes of the symmetric group on n points.
EXAMPLES:
sage: v = Partitions(5).list(); v
[[5], [4, 1], [3, 2], [3, 1, 1], [2, 2, 1], [2, 1, 1, 1], [1, 1, 1, 1, 1]]
sage: len(v)
7
sage: Partitions(5).cardinality(algorithm='gap')
7
sage: Partitions(5).cardinality(algorithm='pari')
7
sage: Partitions(5).cardinality(algorithm='bober')
7
The input must be a nonnegative integer or a ValueError is raised.
sage: Partitions(10).cardinality()
42
sage: Partitions(3).cardinality()
3
sage: Partitions(10).cardinality()
42
sage: Partitions(3).cardinality(algorithm='pari')
3
sage: Partitions(10).cardinality(algorithm='pari')
42
sage: Partitions(40).cardinality()
37338
sage: Partitions(100).cardinality()
190569292
A generating function for p(n) is given by the reciprocal of Euler’s function:
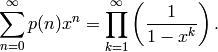
We use Sage to verify that the first several coefficients do instead agree:
sage: q = PowerSeriesRing(QQ, 'q', default_prec=9).gen()
sage: prod([(1-q^k)^(-1) for k in range(1,9)]) ## partial product of
1 + q + 2*q^2 + 3*q^3 + 5*q^4 + 7*q^5 + 11*q^6 + 15*q^7 + 22*q^8 + O(q^9)
sage: [Partitions(k) .cardinality()for k in range(2,10)]
[2, 3, 5, 7, 11, 15, 22, 30]
REFERENCES:
Returns the lexicographically first partition of a positive integer n. This is the partition [n].
EXAMPLES:
sage: Partitions(4).first()
[4]
Returns the lexicographically last partition of the positive integer n. This is the all-ones partition.
EXAMPLES:
sage: Partitions(4).last()
[1, 1, 1, 1]
Returns a random partitions of  for the specified measure.
for the specified measure.
INPUT:
measure -
- uniform - (default) pick a element for the uniform mesure.
- Plancherel - use plancherel measure.
EXAMPLES:
sage: Partitions(5).random_element() # random
[2, 1, 1, 1]
sage: Partitions(5).random_element(measure='Plancherel') # random
[2, 1, 1, 1]
Returns a random partitions of  .
.
EXAMPLES:
sage: Partitions(5).random_element_plancherel() # random
[2, 1, 1, 1]
sage: Partitions(20).random_element_plancherel() # random
[9, 3, 3, 2, 2, 1]
TESTS:
sage: all(Part.random_element_plancherel() in Part
... for Part in map(Partitions, range(10)))
True
ALGORITHM:
- insert by robinson-schensted a uniform random permutations of n and returns the shape of the resulting tableau. The complexity is
which is likely optimal. However, the implementation could be optimized.
AUTHOR:
- Florent Hivert (2009-11-23)
Returns a random partitions of  with uniform probability.
with uniform probability.
EXAMPLES:
sage: Partitions(5).random_element_uniform() # random
[2, 1, 1, 1]
sage: Partitions(20).random_element_uniform() # random
[9, 3, 3, 2, 2, 1]
TESTS:
sage: all(Part.random_element_uniform() in Part
... for Part in map(Partitions, range(10)))
True
ALGORITHM:
- It is a python Implementation of RANDPAR, see [nw] below. The complexity is unkown, there may be better algorithms. TODO: Check in Knuth AOCP4.
- There is also certainly a lot of room for optimizations, see comments in the code.
REFERENCES:
- [nw] Nijenhuis, Wilf, Combinatorial Algorithms, Academic Press (1978).
AUTHOR:
- Florent Hivert (2009-11-23)
Bases: sage.combinat.combinat.CombinatorialClass
Return the number of partitions with parts in  . Wraps GAP’s
NrRestrictedPartitions.
. Wraps GAP’s
NrRestrictedPartitions.
EXAMPLES:
sage: Partitions(15, parts_in=[2,3,7]).cardinality()
5
If you can use all parts 1 through  , we’d better get
, we’d better get 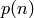 :
:
sage: Partitions(20, parts_in=[1..20]).cardinality() == Partitions(20).cardinality()
True
TESTS:
Let’s check the consistency of GAP’s function and our own algorithm that actually generates the partitions.
sage: ps = Partitions(15, parts_in=[1,2,3])
sage: ps.cardinality() == len(ps.list())
True
sage: ps = Partitions(15, parts_in=[])
sage: ps.cardinality() == len(ps.list())
True
sage: ps = Partitions(3000, parts_in=[50,100,500,1000])
sage: ps.cardinality() == len(ps.list())
True
sage: ps = Partitions(10, parts_in=[3,6,9])
sage: ps.cardinality() == len(ps.list())
True
sage: ps = Partitions(0, parts_in=[1,2])
sage: ps.cardinality() == len(ps.list())
True
Return the lexicographically first partition of a positive
integer  with the specified parts, or None if no such
partition exists.
with the specified parts, or None if no such
partition exists.
EXAMPLES:
sage: Partitions(9, parts_in=[3,4]).first()
[3, 3, 3]
sage: Partitions(6, parts_in=[1..6]).first()
[6]
sage: Partitions(30, parts_in=[4,7,8,10,11]).first()
[11, 11, 8]
Returns the lexicographically last partition of the positive
integer  with the specified parts, or None if no such
partition exists.
with the specified parts, or None if no such
partition exists.
EXAMPLES:
sage: Partitions(15, parts_in=[2,3]).last()
[3, 2, 2, 2, 2, 2, 2]
sage: Partitions(30, parts_in=[4,7,8,10,11]).last()
[7, 7, 4, 4, 4, 4]
sage: Partitions(10, parts_in=[3,6]).last() is None
True
sage: Partitions(50, parts_in=[11,12,13]).last()
[13, 13, 12, 12]
sage: Partitions(30, parts_in=[4,7,8,10,11]).last()
[7, 7, 4, 4, 4, 4]
TESTS:
sage: Partitions(6, parts_in=[1..6]).last()
[1, 1, 1, 1, 1, 1]
sage: Partitions(0, parts_in=[]).last()
[]
sage: Partitions(50, parts_in=[11,12]).last() is None
True
Bases: sage.combinat.combinat.CombinatorialClass
EXAMPLES:
sage: Partitions(3, starting=[2,1]).first()
[2, 1]
EXAMPLES:
sage: Partitions(3, starting=[2,1]).next(Partition([2,1]))
[1, 1, 1]
This function has been deprecated and will be removed in a future version of Sage; use Partitions() with the parts_in keyword.
Original docstring follows.
A restricted partition is, like an ordinary partition, an unordered
sum 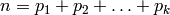 of positive integers and is
represented by the list
of positive integers and is
represented by the list ![p = [p_1,p_2,\ldots,p_k]](../../_images/math/5a7ae185b982284bb0098dcb16f5deac9a6e0216.png) , in
nonincreasing order. The difference is that here the
, in
nonincreasing order. The difference is that here the 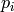 must be elements from the set
must be elements from the set  , while for ordinary
partitions they may be elements from
, while for ordinary
partitions they may be elements from ![[1..n]](../../_images/math/661645d786e38486f3e060af5d4aac31188ecddf.png) .
.
Returns the list of all restricted partitions of the positive integer n into sums with k summands with the summands of the partition coming from the set S. If k is not given all restricted partitions for all k are returned.
Wraps GAP’s RestrictedPartitions.
EXAMPLES:
sage: RestrictedPartitions(5,[3,2,1])
doctest:...: DeprecationWarning: RestrictedPartitions is deprecated; use Partitions with the parts_in keyword instead.
doctest:...: DeprecationWarning: RestrictedPartitions_nsk is deprecated; use Partitions with the parts_in keyword instead.
Partitions of 5 restricted to the values [1, 2, 3]
sage: RestrictedPartitions(5,[3,2,1]).list()
[[3, 2], [3, 1, 1], [2, 2, 1], [2, 1, 1, 1], [1, 1, 1, 1, 1]]
sage: RestrictedPartitions(5,[3,2,1],4)
Partitions of 5 restricted to the values [1, 2, 3] of length 4
sage: RestrictedPartitions(5,[3,2,1],4).list()
[[2, 1, 1, 1]]
Bases: sage.combinat.combinat.CombinatorialClass
We are deprecating RestrictedPartitions, so this class should be deprecated too.
Returns the size of RestrictedPartitions(n,S,k). Wraps GAP’s NrRestrictedPartitions.
EXAMPLES:
sage: RestrictedPartitions(8,[1,3,5,7]).cardinality()
doctest:...: DeprecationWarning: RestrictedPartitions is deprecated; use Partitions with the parts_in keyword instead.
6
sage: RestrictedPartitions(8,[1,3,5,7],2).cardinality()
2
Returns the list of all restricted partitions of the positive
integer n into sums with k summands with the summands of the
partition coming from the set  . If k is not given all
restricted partitions for all k are returned.
. If k is not given all
restricted partitions for all k are returned.
Wraps GAP’s RestrictedPartitions.
EXAMPLES:
sage: RestrictedPartitions(8,[1,3,5,7]).list()
doctest:...: DeprecationWarning: RestrictedPartitions is deprecated; use Partitions with the parts_in keyword instead.
[[7, 1], [5, 3], [5, 1, 1, 1], [3, 3, 1, 1], [3, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1]]
sage: RestrictedPartitions(8,[1,3,5,7],2).list()
[[7, 1], [5, 3]]
Returns all combinations of cyclic permutations of each cell of the partition.
AUTHORS:
EXAMPLES:
sage: from sage.combinat.partition import cyclic_permutations_of_partition
sage: cyclic_permutations_of_partition([[1,2,3,4],[5,6,7]])
[[[1, 2, 3, 4], [5, 6, 7]],
[[1, 2, 4, 3], [5, 6, 7]],
[[1, 3, 2, 4], [5, 6, 7]],
[[1, 3, 4, 2], [5, 6, 7]],
[[1, 4, 2, 3], [5, 6, 7]],
[[1, 4, 3, 2], [5, 6, 7]],
[[1, 2, 3, 4], [5, 7, 6]],
[[1, 2, 4, 3], [5, 7, 6]],
[[1, 3, 2, 4], [5, 7, 6]],
[[1, 3, 4, 2], [5, 7, 6]],
[[1, 4, 2, 3], [5, 7, 6]],
[[1, 4, 3, 2], [5, 7, 6]]]
Note that repeated elements are not considered equal:
sage: cyclic_permutations_of_partition([[1,2,3],[4,4,4]])
[[[1, 2, 3], [4, 4, 4]],
[[1, 3, 2], [4, 4, 4]],
[[1, 2, 3], [4, 4, 4]],
[[1, 3, 2], [4, 4, 4]]]
Iterates over all combinations of cyclic permutations of each cell of the partition.
AUTHORS:
EXAMPLES:
sage: from sage.combinat.partition import cyclic_permutations_of_partition
sage: list(cyclic_permutations_of_partition_iterator([[1,2,3,4],[5,6,7]]))
[[[1, 2, 3, 4], [5, 6, 7]],
[[1, 2, 4, 3], [5, 6, 7]],
[[1, 3, 2, 4], [5, 6, 7]],
[[1, 3, 4, 2], [5, 6, 7]],
[[1, 4, 2, 3], [5, 6, 7]],
[[1, 4, 3, 2], [5, 6, 7]],
[[1, 2, 3, 4], [5, 7, 6]],
[[1, 2, 4, 3], [5, 7, 6]],
[[1, 3, 2, 4], [5, 7, 6]],
[[1, 3, 4, 2], [5, 7, 6]],
[[1, 4, 2, 3], [5, 7, 6]],
[[1, 4, 3, 2], [5, 7, 6]]]
Note that repeated elements are not considered equal:
sage: list(cyclic_permutations_of_partition_iterator([[1,2,3],[4,4,4]]))
[[[1, 2, 3], [4, 4, 4]],
[[1, 3, 2], [4, 4, 4]],
[[1, 2, 3], [4, 4, 4]],
[[1, 3, 2], [4, 4, 4]]]
Return the Ferrers diagram of pi.
INPUT:
EXAMPLES:
sage: print Partition([5,5,2,1]).ferrers_diagram()
*****
*****
**
*
** This function is being deprecated - use Partition(core=*, quotient=*) instead **
Returns a partition from its core and quotient.
Algorithm from mupad-combinat.
Note
This function is for internal use only; use Partition(core=*, quotient=*) instead.
EXAMPLES:
sage: Partition(core=[2,1], quotient=[[2,1],[3],[1,1,1]])
[11, 5, 5, 3, 2, 2, 2]
Returns a partition from its list of multiplicities.
Note
This function is for internal use only; use Partition(exp=*) instead.
EXAMPLES:
sage: Partition(exp=[1,2,1])
[3, 2, 2, 1]
Returns the size of ordered_partitions(n,k). Wraps GAP’s NrOrderedPartitions.
It is possible to associate with every partition of the integer n a conjugacy class of permutations in the symmetric group on n points and vice versa. Therefore p(n) = NrPartitions(n) is the number of conjugacy classes of the symmetric group on n points.
EXAMPLES:
sage: number_of_ordered_partitions(10,2)
9
sage: number_of_ordered_partitions(15)
16384
Returns the size of partitions_list(n,k).
INPUT:
 is in the thousands, in which case PARI is
faster. But PARI has a bug, e.g., on 64-bit Linux
PARI-2.3.2 outputs numbpart(147007)%1000 as 536 when it should
be 533!. So do not use this option.
is in the thousands, in which case PARI is
faster. But PARI has a bug, e.g., on 64-bit Linux
PARI-2.3.2 outputs numbpart(147007)%1000 as 536 when it should
be 533!. So do not use this option.IMPLEMENTATION: Wraps GAP’s NrPartitions or PARI’s numbpart function.
Use the function partitions(n) to return a
generator over all partitions of  .
.
It is possible to associate with every partition of the integer n a conjugacy class of permutations in the symmetric group on n points and vice versa. Therefore p(n) = NrPartitions(n) is the number of conjugacy classes of the symmetric group on n points.
EXAMPLES:
sage: v = list(partitions(5)); v
[(1, 1, 1, 1, 1), (1, 1, 1, 2), (1, 2, 2), (1, 1, 3), (2, 3), (1, 4), (5,)]
sage: len(v)
7
sage: number_of_partitions(5, algorithm='gap')
7
sage: number_of_partitions(5, algorithm='pari')
7
sage: number_of_partitions(5, algorithm='bober')
7
The input must be a nonnegative integer or a ValueError is raised.
sage: number_of_partitions(-5)
...
ValueError: n (=-5) must be a nonnegative integer
sage: number_of_partitions(10,2)
5
sage: number_of_partitions(10)
42
sage: number_of_partitions(3)
3
sage: number_of_partitions(10)
42
sage: number_of_partitions(3, algorithm='pari')
3
sage: number_of_partitions(10, algorithm='pari')
42
sage: number_of_partitions(40)
37338
sage: number_of_partitions(100)
190569292
sage: number_of_partitions(100000)
27493510569775696512677516320986352688173429315980054758203125984302147328114964173055050741660736621590157844774296248940493063070200461792764493033510116079342457190155718943509725312466108452006369558934464248716828789832182345009262853831404597021307130674510624419227311238999702284408609370935531629697851569569892196108480158600569421098519
A generating function for p(n) is given by the reciprocal of Euler’s function:
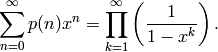
We use Sage to verify that the first several coefficients do instead agree:
sage: q = PowerSeriesRing(QQ, 'q', default_prec=9).gen()
sage: prod([(1-q^k)^(-1) for k in range(1,9)]) ## partial product of
1 + q + 2*q^2 + 3*q^3 + 5*q^4 + 7*q^5 + 11*q^6 + 15*q^7 + 22*q^8 + O(q^9)
sage: [number_of_partitions(k) for k in range(2,10)]
[2, 3, 5, 7, 11, 15, 22, 30]
REFERENCES:
TESTS:
sage: n = 500 + randint(0,500)
sage: number_of_partitions( n - (n % 385) + 369) % 385 == 0
True
sage: n = 1500 + randint(0,1500)
sage: number_of_partitions( n - (n % 385) + 369) % 385 == 0
True
sage: n = 1000000 + randint(0,1000000)
sage: number_of_partitions( n - (n % 385) + 369) % 385 == 0
True
sage: n = 1000000 + randint(0,1000000)
sage: number_of_partitions( n - (n % 385) + 369) % 385 == 0
True
sage: n = 1000000 + randint(0,1000000)
sage: number_of_partitions( n - (n % 385) + 369) % 385 == 0
True
sage: n = 1000000 + randint(0,1000000)
sage: number_of_partitions( n - (n % 385) + 369) % 385 == 0
True
sage: n = 1000000 + randint(0,1000000)
sage: number_of_partitions( n - (n % 385) + 369) % 385 == 0
True
sage: n = 1000000 + randint(0,1000000)
sage: number_of_partitions( n - (n % 385) + 369) % 385 == 0
True
sage: n = 100000000 + randint(0,100000000)
sage: number_of_partitions( n - (n % 385) + 369) % 385 == 0
True
sage: n = 1000000000 + randint(0,1000000000)
sage: number_of_partitions( n - (n % 385) + 369) % 385 == 0 # takes a long time
True
Another consistency test for n up to 500:
sage: len([n for n in [1..500] if number_of_partitions(n) != number_of_partitions(n,algorithm='pari')])
0
This function will be deprecated in a future version of Sage and eventually removed. Use Partitions(n).cardinality() or Partitions(n, length=k).cardinality() instead.
Original docstring follows.
Returns the size of partitions_list(n,k).
Wraps GAP’s NrPartitions.
It is possible to associate with every partition of the integer n a conjugacy class of permutations in the symmetric group on n points and vice versa. Therefore p(n) = NrPartitions(n) is the number of conjugacy classes of the symmetric group on n points.
number_of_partitions(n) is also available in
PARI, however the speed seems the same until  is in the
thousands (in which case PARI is faster).
is in the
thousands (in which case PARI is faster).
EXAMPLES:
sage: partition.number_of_partitions_list(10,2)
5
sage: partition.number_of_partitions_list(10)
42
A generating function for p(n) is given by the reciprocal of Euler’s function:
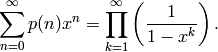
Sage verifies that the first several coefficients do instead agree:
sage: q = PowerSeriesRing(QQ, 'q', default_prec=9).gen()
sage: prod([(1-q^k)^(-1) for k in range(1,9)]) ## partial product of
1 + q + 2*q^2 + 3*q^3 + 5*q^4 + 7*q^5 + 11*q^6 + 15*q^7 + 22*q^8 + O(q^9)
sage: [partition.number_of_partitions_list(k) for k in range(2,10)]
[2, 3, 5, 7, 11, 15, 22, 30]
REFERENCES:
This function will be deprecated in a future version of Sage and eventually removed. Use RestrictedPartitions(n, S, k).cardinality() instead.
Original docstring follows.
Returns the size of partitions_restricted(n,S,k). Wraps GAP’s NrRestrictedPartitions.
EXAMPLES:
sage: number_of_partitions_restricted(8,[1,3,5,7])
6
sage: number_of_partitions_restricted(8,[1,3,5,7],2)
2
Returns the size of partitions_set(S,k). Wraps GAP’s NrPartitionsSet.
The Stirling number of the second kind is the number of partitions of a set of size n into k blocks.
EXAMPLES:
sage: mset = [1,2,3,4]
sage: number_of_partitions_set(mset,2)
7
sage: stirling_number2(4,2)
7
REFERENCES
number_of_partition_tuples( n, k ) returns the number of partition_tuples(n,k).
Wraps GAP’s NrPartitionTuples.
EXAMPLES:
sage: number_of_partitions_tuples(3,2)
10
sage: number_of_partitions_tuples(8,2)
185
Now we compare that with the result of the following GAP computation:
gap> S8:=Group((1,2,3,4,5,6,7,8),(1,2));
Group([ (1,2,3,4,5,6,7,8), (1,2) ])
gap> C2:=Group((1,2));
Group([ (1,2) ])
gap> W:=WreathProduct(C2,S8);
<permutation group of size 10321920 with 10 generators>
gap> Size(W);
10321920 ## = 2^8*Factorial(8), which is good:-)
gap> Size(ConjugacyClasses(W));
185
An ordered partition of  is an ordered sum
is an ordered sum
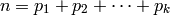
of positive integers and is represented by the list
![p = [p_1,p_2,\cdots ,p_k]](../../_images/math/d2cebf8b552a99c3e826f03a4a6525680bbdeafd.png) . If
. If  is omitted
then all ordered partitions are returned.
is omitted
then all ordered partitions are returned.
ordered_partitions(n,k) returns the list of all (ordered) partitions of the positive integer n into sums with k summands.
Do not call ordered_partitions with an n much larger than 15, since the list will simply become too large.
Wraps GAP’s OrderedPartitions.
The number of ordered partitions 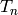 of
of
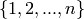 has the generating function is
has the generating function is
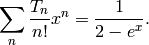
EXAMPLES:
sage: ordered_partitions(10,2)
[[1, 9], [2, 8], [3, 7], [4, 6], [5, 5], [6, 4], [7, 3], [8, 2], [9, 1]]
sage: ordered_partitions(4)
[[1, 1, 1, 1], [1, 1, 2], [1, 2, 1], [1, 3], [2, 1, 1], [2, 2], [3, 1], [4]]
REFERENCES:
** This function is being deprecated – use Partition(*).conjugate() instead. **
partition_associated( pi ) returns the “associated” (also called “conjugate” in the literature) partition of the partition pi which is obtained by transposing the corresponding Ferrers diagram.
EXAMPLES:
sage: Partition([2,2]).conjugate()
[2, 2]
sage: Partition([6,3,1]).conjugate()
[3, 2, 2, 1, 1, 1]
sage: print Partition([6,3,1]).ferrers_diagram()
******
***
*
sage: print Partition([6,3,1]).conjugate().ferrers_diagram()
***
**
**
*
*
*
partition_power( pi, k ) returns the partition corresponding to
the  -th power of a permutation with cycle structure pi
(thus describes the powermap of symmetric groups).
-th power of a permutation with cycle structure pi
(thus describes the powermap of symmetric groups).
Wraps GAP’s PowerPartition.
EXAMPLES:
sage: partition_power([5,3],1)
[5, 3]
sage: partition_power([5,3],2)
[5, 3]
sage: partition_power([5,3],3)
[5, 1, 1, 1]
sage: partition_power([5,3],4)
[5, 3]
Now let us compare this to the power map on 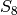 :
:
sage: G = SymmetricGroup(8)
sage: g = G([(1,2,3,4,5),(6,7,8)])
sage: g
(1,2,3,4,5)(6,7,8)
sage: g^2
(1,3,5,2,4)(6,8,7)
sage: g^3
(1,4,2,5,3)
sage: g^4
(1,5,4,3,2)(6,7,8)
** This function is being deprecated – use Partition(*).sign() instead. **
Partition( pi ).sign() returns the sign of a permutation with cycle structure given by the partition pi.
This function corresponds to a homomorphism from the symmetric
group 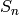 into the cyclic group of order 2, whose kernel
is exactly the alternating group
into the cyclic group of order 2, whose kernel
is exactly the alternating group 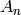 . Partitions of sign
. Partitions of sign
 are called even partitions while partitions of sign
are called even partitions while partitions of sign
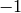 are called odd.
are called odd.
This function is deprecated: use Partition( pi ).sign() instead.
EXAMPLES:
sage: Partition([5,3]).sign()
1
sage: Partition([5,2]).sign()
-1
Zolotarev’s lemma states that the Legendre symbol
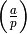 for an integer
for an integer
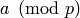 (
( a prime number), can be computed
as sign(p_a), where sign denotes the sign of a permutation and
p_a the permutation of the residue classes
a prime number), can be computed
as sign(p_a), where sign denotes the sign of a permutation and
p_a the permutation of the residue classes  induced by modular multiplication by
induced by modular multiplication by  , provided
, provided
 does not divide
does not divide  .
.
We verify this in some examples.
sage: F = GF(11)
sage: a = F.multiplicative_generator();a
2
sage: plist = [int(a*F(x)) for x in range(1,11)]; plist
[2, 4, 6, 8, 10, 1, 3, 5, 7, 9]
This corresponds to the permutation (1, 2, 4, 8, 5, 10, 9, 7, 3, 6)
(acting the set 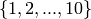 ) and to the partition
[10].
) and to the partition
[10].
sage: p = PermutationGroupElement('(1, 2, 4, 8, 5, 10, 9, 7, 3, 6)')
sage: p.sign()
-1
sage: Partition([10]).sign()
-1
sage: kronecker_symbol(11,2)
-1
Now replace  by
by 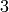 :
:
sage: plist = [int(F(3*x)) for x in range(1,11)]; plist
[3, 6, 9, 1, 4, 7, 10, 2, 5, 8]
sage: range(1,11)
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
sage: p = PermutationGroupElement('(3,4,8,7,9)')
sage: p.sign()
1
sage: kronecker_symbol(3,11)
1
sage: Partition([5,1,1,1,1,1]).sign()
1
In both cases, Zolotarev holds.
REFERENCES:
Generator of all the partitions of the integer  .
.
INPUT:
To compute the number of partitions of  use
number_of_partitions(n).
use
number_of_partitions(n).
EXAMPLES:
sage: partitions(3)
<generator object partitions at 0x...>
sage: list(partitions(3))
[(1, 1, 1), (1, 2), (3,)]
AUTHORS:
Returns the list of all (unordered) “restricted” partitions of the integer n having parts less than or equal to the integer k.
Wraps GAP’s PartitionsGreatestLE.
EXAMPLES:
sage: partitions_greatest(10,2)
[[1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[2, 1, 1, 1, 1, 1, 1, 1, 1],
[2, 2, 1, 1, 1, 1, 1, 1],
[2, 2, 2, 1, 1, 1, 1],
[2, 2, 2, 2, 1, 1],
[2, 2, 2, 2, 2]]
Returns the list of all (unordered) “restricted” partitions of the integer n having at least one part equal to the integer k.
Wraps GAP’s PartitionsGreatestEQ.
EXAMPLES:
sage: partitions_greatest_eq(10,2)
[[2, 1, 1, 1, 1, 1, 1, 1, 1],
[2, 2, 1, 1, 1, 1, 1, 1],
[2, 2, 2, 1, 1, 1, 1],
[2, 2, 2, 2, 1, 1],
[2, 2, 2, 2, 2]]
This function will be deprecated in a future version of Sage and eventually removed. Use Partitions(n).list() or Partitions(n, length=k).list() instead.
Original docstring follows.
An unordered partition of  is an unordered sum
is an unordered sum
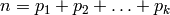 of positive integers and is
represented by the list
of positive integers and is
represented by the list ![p = [p_1,p_2,\ldots,p_k]](../../_images/math/5a7ae185b982284bb0098dcb16f5deac9a6e0216.png) , in
nonincreasing order, i.e.,
, in
nonincreasing order, i.e., 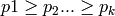 .
.
INPUT:
partitions_list(n,k) returns the list of all (unordered) partitions of the positive integer n into sums with k summands. If k is omitted then all partitions are returned.
Do not call partitions_list with an n much larger than 40, in which case there are 37338 partitions, since the list will simply become too large.
Wraps GAP’s Partitions.
EXAMPLES:
sage: partitions_list(10,2)
[[5, 5], [6, 4], [7, 3], [8, 2], [9, 1]]
sage: partitions_list(5)
[[1, 1, 1, 1, 1], [2, 1, 1, 1], [2, 2, 1], [3, 1, 1], [3, 2], [4, 1], [5]]
This function will be deprecated in a future version of Sage and eventually removed. Use RestrictedPartitions(n, S, k).list() instead.
Original docstring follows.
A restricted partition is, like an ordinary partition, an unordered
sum 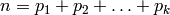 of positive integers and is
represented by the list
of positive integers and is
represented by the list ![p = [p_1,p_2,\ldots,p_k]](../../_images/math/5a7ae185b982284bb0098dcb16f5deac9a6e0216.png) , in
nonincreasing order. The difference is that here the
, in
nonincreasing order. The difference is that here the 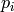 must be elements from the set
must be elements from the set  , while for ordinary
partitions they may be elements from
, while for ordinary
partitions they may be elements from ![[1..n]](../../_images/math/661645d786e38486f3e060af5d4aac31188ecddf.png) .
.
Returns the list of all restricted partitions of the positive
integer n into sums with k summands with the summands of the
partition coming from the set  . If k is not given all
restricted partitions for all k are returned.
. If k is not given all
restricted partitions for all k are returned.
Wraps GAP’s RestrictedPartitions.
EXAMPLES:
sage: partitions_restricted(8,[1,3,5,7])
[[1, 1, 1, 1, 1, 1, 1, 1],
[3, 1, 1, 1, 1, 1],
[3, 3, 1, 1],
[5, 1, 1, 1],
[5, 3],
[7, 1]]
sage: partitions_restricted(8,[1,3,5,7],2)
[[5, 3], [7, 1]]
An unordered partition of a set  is a set of pairwise
disjoint nonempty subsets with union
is a set of pairwise
disjoint nonempty subsets with union  and is represented
by a sorted list of such subsets.
and is represented
by a sorted list of such subsets.
partitions_set returns the list of all unordered partitions of the
list  of increasing positive integers into k pairwise
disjoint nonempty sets. If k is omitted then all partitions are
returned.
of increasing positive integers into k pairwise
disjoint nonempty sets. If k is omitted then all partitions are
returned.
The Bell number 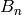 , named in honor of Eric Temple Bell,
is the number of different partitions of a set with n elements.
, named in honor of Eric Temple Bell,
is the number of different partitions of a set with n elements.
Warning
Wraps GAP - hence S must be a list of objects that have string representations that can be interpreted by the GAP interpreter. If mset consists of at all complicated Sage objects, this function does not do what you expect. See SetPartitions in combinat/set_partition.
Warning
This function is inefficient. The runtime is dominated by parsing the output from GAP.
Wraps GAP’s PartitionsSet.
EXAMPLES:
sage: S = [1,2,3,4]
sage: partitions_set(S,2)
[[[1], [2, 3, 4]],
[[1, 2], [3, 4]],
[[1, 2, 3], [4]],
[[1, 2, 4], [3]],
[[1, 3], [2, 4]],
[[1, 3, 4], [2]],
[[1, 4], [2, 3]]]
REFERENCES:
partition_tuples( n, k ) returns the list of all k-tuples of partitions which together form a partition of n.
k-tuples of partitions describe the classes and the characters of
wreath products of groups with k conjugacy classes with the
symmetric group 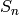 .
.
Wraps GAP’s PartitionTuples.
EXAMPLES:
sage: partitions_tuples(3,2)
[[[1, 1, 1], []],
[[1, 1], [1]],
[[1], [1, 1]],
[[], [1, 1, 1]],
[[2, 1], []],
[[1], [2]],
[[2], [1]],
[[], [2, 1]],
[[3], []],
[[], [3]]]