Fast Rank Two Crystals

class sage.combinat.crystals.fast_crystals.FastCrystal(ct, shape, format)

Bases: sage.structure.unique_representation.UniqueRepresentation, sage.structure.parent.Parent

An alternative implementation of rank 2 crystals. The root operators are implemented in memory by table lookup. This means that in comparison with the CrystalsOfTableaux, these crystals are slow to instantiate but faster for computation. Implemented for types A2, B2 and C2.

Input: CartanType and a shape. The CartanType is [‘A’,2], [‘B’,2] or [‘C’,2]. The shape is of the form [l1,l2] where l1 and l2 are either integers or (in type B) half integers such that l1-l2 is integral. It is assumed that l1 >= l2 >= 0. If l1 and l2 are integers, this will produce the a crystal isomorphic to the one obtained by CrystalOfTableaux(type, shape=[l1,l2]). Furthermore FastCrystal([‘B’, 2], l1+1/2, l2+1/2) produces a crystal isomorphic to the following crystal T:

C = CrystalOfTableaux(['B',2], shape=[l1,l2])
D = CrystalOfSpins(['B',2])
T = TensorProductOfCrystals(C,D,C.list()[0],D.list()[0])

The representation of elements is in term of the Berenstein-Zelevinsky-Littelmann strings [a1, a2, ...] described under metapost in crystals.py. Alternative representations may be obtained by the options format=”dual_string” or format=”simple”. In the simple format, the element is represented by and integer, and in the dual_string format, it is represented by the Berenstein-Zelevinsky-Littelmann string, but the underlying decomposition of the long Weyl group element into simple reflections is changed.

TESTS:

sage: C = FastCrystal(['A',2],shape=[4,1])
sage: C.cardinality()
24
sage: C.cartan_type()
['A', 2]
sage: TestSuite(C).run()
sage: C = FastCrystal(['B',2],shape=[4,1])
sage: C.cardinality()
154
sage: TestSuite(C).run()
sage: C = FastCrystal(['B',2],shape=[3/2,1/2])
sage: C.cardinality()
16
sage: TestSuite(C).run()
sage: C = FastCrystal(['C',2],shape=[2,1])
sage: C.cardinality()
16
sage: C = FastCrystal(['C',2],shape=[3,1])
sage: C.cardinality()
35
sage: TestSuite(C).run()

class Element(parent, value, format)

Bases: sage.structure.element.Element

e(i)

Returns the action of 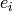on self.

EXAMPLES:

sage: C = FastCrystal(['A',2],shape=[2,1])
sage: C(1).e(1)
[0, 0, 0]
sage: C(0).e(1) is None
True

f(i)

Returns the action of 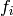on self.

EXAMPLES:

sage: C = FastCrystal(['A',2],shape=[2,1])
sage: C(6).f(1)
[1, 2, 1]
sage: C(7).f(1) is None
True

weight()

Returns the weight of self.

EXAMPLES:

sage: [v.weight() for v in FastCrystal(['A',2], shape=[2,1])]
[(2, 1, 0), (1, 2, 0), (1, 1, 1), (1, 0, 2), (0, 1, 2), (2, 0, 1), (1, 1, 1), (0, 2, 1)]
sage: [v.weight() for v in FastCrystal(['B',2], shape=[1,0])]
[(1, 0), (0, 1), (0, 0), (0, -1), (-1, 0)]
sage: [v.weight() for v in FastCrystal(['B',2], shape=[1/2,1/2])]
[(1/2, 1/2), (1/2, -1/2), (-1/2, 1/2), (-1/2, -1/2)]
sage: [v.weight() for v in FastCrystal(['C',2], shape=[1,0])]
[(1, 0), (0, 1), (0, -1), (-1, 0)]
sage: [v.weight() for v in FastCrystal(['C',2], shape=[1,1])]
[(1, 1), (1, -1), (0, 0), (-1, 1), (-1, -1)]

FastCrystal.cmp_elements(x, y)

Returns True if and only if there is a path from x to y in the crystal graph.

Because the crystal graph is classical, it is a directed acyclic graph which can be interpreted as a poset. This function implements the comparison function of this poset.

EXAMPLES:

sage: C = FastCrystal(['A',2],shape=[2,1])
sage: x = C(0)
sage: y = C(1)
sage: C.cmp_elements(x,y)
-1
sage: C.cmp_elements(y,x)
1
sage: C.cmp_elements(x,x)
0

FastCrystal.digraph()

Returns the digraph associated to self.

EXAMPLES:

sage: C = FastCrystal(['A',2],shape=[2,1])
sage: C.digraph()
Digraph on 8 vertices

FastCrystal.list()

Returns a list of the elements of self.

EXAMPLES:

sage: C = FastCrystal(['A',2],shape=[2,1])
sage: C.list()
[[0, 0, 0],
 [1, 0, 0],
 [0, 1, 1],
 [0, 2, 1],
 [1, 2, 1],
 [0, 1, 0],
 [1, 1, 0],
 [2, 1, 0]]