Crystals

Let 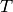be a CartanType with index set , and 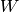be a realization of the typ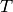e weight lattice.

A type 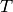crystal 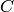is a colored oriented graph equipped with a weight function from the nodes to some realization of the type 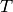weight lattice such that:

• Each edge is colored with a label in .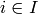

• For each , each node has:

  • at most one -successor ;
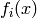  • at most one -predecessor .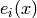

  Furthermore, when they exist,

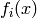  • .weight() = x.weight() - ;
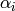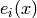  • .weight() = x.weight() + .

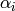This crystal actually models a representation of a Lie algebra if it satisfies some further local conditions due to Stembridge [St2003].

REFERENCES:

[St2003]

J. Stembridge, A local characterization of simply-laced crystals, Trans. Amer. Math. Soc. 355 (2003), no. 12, 4807-4823.

EXAMPLES:

We construct the type 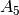crystal on letters (or in representation theoretic terms, the highest weight crystal of type 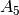corresponding to the highest weight ):

sage: C = CrystalOfLetters(['A',5]); C
The crystal of letters for type ['A', 5]

It has a single highest weight element:

sage: C.highest_weight_vectors()
[1]

A crystal is an enumerated set (see EnumeratedSets); and we can count and list its elements in the usual way:

sage: C.cardinality()
6
sage: C.list()
[1, 2, 3, 4, 5, 6]

as well as use it in for loops:

sage: [x for x in C]
[1, 2, 3, 4, 5, 6]

Here are some more elaborate crystals (see their respective documentations):

sage: Tens = TensorProductOfCrystals(C, C)
sage: Spin = CrystalOfSpins(['B', 3])
sage: Tab  = CrystalOfTableaux(['A', 3], shape = [2,1,1])
sage: Fast = FastCrystal(['B', 2], shape = [3/2, 1/2])
sage: KR = KirillovReshetikhinCrystal(['A',2,1],1,1)

One can get (currently) crude plotting via:

sage: Tab.plot()

For rank two crystals, there is an alternative method of getting metapost pictures. For more information see C.metapost?

See also the categories Crystals, ClassicalCrystals, FiniteCrystals, HighestWeightCrystals.

Caveat: this crystal library, although relatively featureful for classical crystals, is still in an early development stage, and the syntax details may be subject to changes.

TODO:

• Vocabulary and conventions:
  • elements or vectors of a crystal?
  • For a classical crystal: connected / highest weight / irreducible
  • ...
• More introductory doc explaining the mathematical background
• Layout instructions for plot() for rank 2 types
• Streamlining the latex output
• Littelmann paths and/or alcove paths (this would give us the exceptional types)
• RestrictionOfCrystal

Most of the above features (except Littelmann/alcove paths) are in MuPAD-Combinat (see lib/COMBINAT/crystals.mu), which could provide inspiration.

class sage.combinat.crystals.crystals.CrystalBacktracker(crystal)

Bases: sage.combinat.backtrack.GenericBacktracker