Examples of semigroups

class sage.categories.examples.semigroups.FreeSemigroup(alphabet=('a', 'b', 'c', 'd'))

Bases: sage.structure.unique_representation.UniqueRepresentation, sage.structure.parent.Parent

An example of semigroup.

The purpose of this class is to provide a minimal template for implementing of a semigroup.

EXAMPLES:

sage: S = Semigroups().example("free"); S
An example of a semigroup: the free semigroup generated by ('a', 'b', 'c', 'd')

This is the free semigroup generated by:

sage: S.semigroup_generators()
Family ('a', 'b', 'c', 'd')

and with product given by contatenation:

sage: S('dab') * S('acb')
'dabacb'

TESTS:

sage: TestSuite(S).run(verbose = True)
running ._test_an_element() . . . pass
running ._test_associativity() . . . pass
running ._test_category() . . . pass
running ._test_elements() . . .
  Running the test suite of self.an_element()
  running ._test_category() . . . pass
  running ._test_eq() . . . pass
  running ._test_not_implemented_methods() . . . pass
  running ._test_pickling() . . . pass
  pass
running ._test_elements_eq() . . . pass
running ._test_eq() . . . pass
running ._test_not_implemented_methods() . . . pass
running ._test_pickling() . . . pass
running ._test_some_elements() . . . pass

class Element(value, parent)

Bases: sage.structure.element_wrapper.ElementWrapper

The class for elements of the free semigroup.

FreeSemigroup.an_element()

Returns an element of the semigroup.

EXAMPLES:

sage: F = Semigroups().example('free')
sage: F.an_element()
'abcd'

FreeSemigroup.product(x, y)

Returns the product of x and y in the semigroup, as per Semigroups.ParentMethods.product().

EXAMPLES:

sage: F = Semigroups().example('free')
sage: F.an_element() * F('a')^5
'abcdaaaaa'

FreeSemigroup.semigroup_generators(*args, **kwds)

Returns the generators of the semigroup.

EXAMPLES:

sage: F = Semigroups().example('free')
sage: F.semigroup_generators()
Family ('a', 'b', 'c', 'd')

class sage.categories.examples.semigroups.IncompleteSubquotientSemigroup(category=None)

Bases: sage.structure.unique_representation.UniqueRepresentation, sage.structure.parent.Parent

class Element(value, parent)

Bases: sage.structure.element_wrapper.ElementWrapper

IncompleteSubquotientSemigroup.ambient()

Returns the ambient semigroup.

EXAMPLES:

sage: S = Semigroups().Subquotients().example()
sage: S.ambient()
An example of a semigroup: the left zero semigroup

class sage.categories.examples.semigroups.LeftZeroSemigroup

Bases: sage.structure.unique_representation.UniqueRepresentation, sage.structure.parent.Parent

An example of a semigroup.

This class illustrates a minimal implementation of a semigroup.

EXAMPLES:

sage: S = Semigroups().example(); S
An example of a semigroup: the left zero semigroup

This is the semigroup that contains all sorts of objects:

sage: S.some_elements()
[3, 42, 'a', 3.3999999999999999, 'raton laveur']

with product rule given by 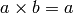for all :

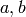sage: S('hello') * S('world')
'hello'
sage: S(3)*S(1)*S(2)
3
sage: S(3)^12312321312321
3

TESTS:

sage: TestSuite(S).run(verbose = True)
running ._test_an_element() . . . pass
running ._test_associativity() . . . pass
running ._test_category() . . . pass
running ._test_elements() . . .
  Running the test suite of self.an_element()
  running ._test_category() . . . pass
  running ._test_eq() . . . pass
  running ._test_not_implemented_methods() . . . pass
  running ._test_pickling() . . . pass
  pass
running ._test_elements_eq() . . . pass
running ._test_eq() . . . pass
running ._test_not_implemented_methods() . . . pass
running ._test_pickling() . . . pass
running ._test_some_elements() . . . pass

class Element(value, parent)

Bases: sage.structure.element_wrapper.ElementWrapper

is_idempotent()

Trivial implementation of Semigroups.Element.is_idempotent since all elements of this semigroup are idempotent!

EXAMPLES:

sage: S = Semigroups().example()
sage: S.an_element().is_idempotent()
True
sage: S(17).is_idempotent()
True

LeftZeroSemigroup.an_element()

Returns an element of the semigroup.

EXAMPLES:

sage: Semigroups().example().an_element()
42

LeftZeroSemigroup.product(x, y)

Returns the product of x and y in the semigroup, as per Semigroups.ParentMethods.product().

EXAMPLES:

sage: S = Semigroups().example()
sage: S('hello') * S('world')
'hello'
sage: S(3)*S(1)*S(2)
3

LeftZeroSemigroup.some_elements()

Returns a list of some elements of the semigroup.

EXAMPLES:

sage: Semigroups().example().some_elements()
[3, 42, 'a', 3.3999999999999999, 'raton laveur']

class sage.categories.examples.semigroups.QuotientOfLeftZeroSemigroup(category=None)

Bases: sage.structure.unique_representation.UniqueRepresentation, sage.structure.parent.Parent

Example of a quotient semigroup

EXAMPLES:

sage: S = Semigroups().Subquotients().example(); S
An example of a (sub)quotient semigroup: a quotient of the left zero semigroup

This is the quotient of:

sage: S.ambient()
An example of a semigroup: the left zero semigroup

obtained by setting 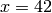for any :

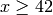sage: S(100)
42
sage: S(100) == S(42)
True

The product is inherited from the ambient semigroup:

sage: S(1)*S(2) == S(1)
True

TESTS:

sage: TestSuite(S).run(verbose = True)
running ._test_an_element() . . . pass
running ._test_associativity() . . . pass
running ._test_category() . . . pass
running ._test_elements() . . .
  Running the test suite of self.an_element()
  running ._test_category() . . . pass
  running ._test_eq() . . . pass
  running ._test_not_implemented_methods() . . . pass
  running ._test_pickling() . . . pass
  pass
running ._test_elements_eq() . . . pass
running ._test_eq() . . . pass
running ._test_not_implemented_methods() . . . pass
running ._test_pickling() . . . pass
running ._test_some_elements() . . . pass

class Element(value, parent)

Bases: sage.structure.element_wrapper.ElementWrapper

QuotientOfLeftZeroSemigroup.ambient()

Returns the ambient semigroup.

EXAMPLES:

sage: S = Semigroups().Subquotients().example()
sage: S.ambient()
An example of a semigroup: the left zero semigroup

QuotientOfLeftZeroSemigroup.an_element()

Returns an element of the semigroup.

EXAMPLES:

sage: S = Semigroups().Subquotients().example()
sage: S.an_element()
42

QuotientOfLeftZeroSemigroup.lift(x)

Lift the element x into the ambient semigroup.

INPUT:

- ``x`` -- an element of ``self``.

OUTPUT:

- an element of ``self.ambient()``.

EXAMPLES:

sage: S = Semigroups().Subquotients().example()
sage: x = S.an_element(); x
42
sage: S.lift(x)
42
sage: S.lift(x) in S.ambient()
True
sage: y = S.ambient()(100); y
100
sage: S.lift(S(y))
42

QuotientOfLeftZeroSemigroup.retract(x)

Returns the retract x onto an element of this semigroup.

INPUT:

- ``x`` -- an element of the ambient semigroup (``self.ambient()``).

OUTPUT:

- an element of ``self``.

EXAMPLES:

sage: S = Semigroups().Subquotients().example()
sage: L = S.ambient()
sage: S.retract(L(17))
17
sage: S.retract(L(42))
42
sage: S.retract(L(171))
42

TESTS:

sage: S.retract(L(171)) in S
True

QuotientOfLeftZeroSemigroup.some_elements()

Returns a list of some elements of the semigroup.

EXAMPLES:

sage: S = Semigroups().Subquotients().example()
sage: S.some_elements()
[1, 2, 3, 8, 42, 42]

QuotientOfLeftZeroSemigroup.the_answer()

Returns the Answer to Life, the Universe, and Everything as an element of this semigroup.

EXAMPLES:

sage: S = Semigroups().Subquotients().example()
sage: S.the_answer()
42