Examples of semigroups in cython

class sage.categories.examples.semigroups_cython.DummyCClass

Bases: object

cpmethod()

TESTS:

sage: from sage.categories.examples.semigroups_cython import DummyCClass
sage: DummyCClass().cpmethod()

method()

TESTS:

sage: from sage.categories.examples.semigroups_cython import DummyCClass
sage: DummyCClass().method()

class sage.categories.examples.semigroups_cython.DummyClass

method()

TESTS:

sage: from sage.categories.examples.semigroups_cython import DummyClass
sage: DummyClass().method()

class sage.categories.examples.semigroups_cython.IdempotentSemigroups(s=None)

Bases: sage.categories.category.Category

ElementMethods

alias of IdempotentSemigroupsElement

super_categories()

EXAMPLES:

sage: from sage.categories.examples.semigroups_cython import IdempotentSemigroups
sage: IdempotentSemigroups().super_categories()
[Category of semigroups]

class sage.categories.examples.semigroups_cython.IdempotentSemigroupsElement

Bases: sage.structure.element.Element

is_idempotent_cpdef()

EXAMPLES:

sage: from sage.categories.examples.semigroups_cython import LeftZeroSemigroup
sage: S = LeftZeroSemigroup()
sage: S(2).is_idempotent_cpdef()  # todo: not implemented (binding; see __getattr__)
True

class sage.categories.examples.semigroups_cython.LeftZeroSemigroup

Bases: sage.categories.examples.semigroups.LeftZeroSemigroup

An example of semigroup

This class illustrates a minimal implementation of a semi-group where the element class is an extension type, and still gets code from the category. Also, the category itself includes some cython methods.

This is purely a proof of concept. The code obviously needs refactorisation!

Comments:

• nested classes seem not to be currently supported by cython
• one cannot play ugly use class surgery tricks (as with _mul_parent) available operations should really be declared to the coercion model!

EXAMPLES:

sage: from sage.categories.examples.semigroups_cython import LeftZeroSemigroup
sage: S = LeftZeroSemigroup(); S
An example of a semigroup: the left zero semigroup

This is the semigroup which contains all sort of objects:

sage: S.some_elements()
[3, 42, 'a', 3.3999999999999999, 'raton laveur']

with product rule is given by 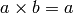for all .

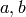sage: S('hello') * S('world')
'hello'

sage: S(3)*S(1)*S(2)
3

sage: S(3)^12312321312321         # todo: not implemented (see __getattr__)
3

sage: TestSuite(S).run(verbose = True)
running ._test_an_element() . . . pass
running ._test_associativity() . . . pass
running ._test_category() . . . pass
running ._test_elements() . . .
  Running the test suite of self.an_element()
  running ._test_category() . . . pass
  running ._test_eq() . . . pass
  running ._test_not_implemented_methods() . . . pass
  running ._test_pickling() . . . pass
  pass
running ._test_elements_eq() . . . pass
running ._test_eq() . . . pass
running ._test_not_implemented_methods() . . . pass
running ._test_pickling() . . . pass
running ._test_some_elements() . . . pass

That’s really the only method which is obtained from the category ...

sage: S(42).is_idempotent
<bound method IdempotentSemigroups.element_class.is_idempotent of 42>
sage: S(42).is_idempotent()
True

sage: S(42)._pow_                 # todo: not implemented (how to bind it?)
<method '_pow_' of 'sage.categories.examples.semigroups_cython.IdempotentSemigroupsElement' objects>
sage: S(42)^10                    # todo: not implemented (see __getattr__)
42

sage: S(42).is_idempotent_cpdef   #  todo: not implemented (how to bind it?)
<method 'is_idempotent_cpdef' of 'sage.categories.examples.semigroups_cython.IdempotentSemigroupsElement' objects>
sage: S(42).is_idempotent_cpdef() # todo: not implemented (see __getattr__)
True

Element

alias of LeftZeroSemigroupElement

class sage.categories.examples.semigroups_cython.LeftZeroSemigroupElement

Bases: sage.structure.element.Element