Affine plane curves over a general ring

AUTHORS:

• William Stein (2005-11-13)
• David Joyner (2005-11-13)
• David Kohel (2006-01)

class sage.schemes.plane_curves.affine_curve.AffineCurve_finite_field(A, f)

Bases: sage.schemes.plane_curves.affine_curve.AffineCurve_generic

rational_points(algorithm='enum')

Return sorted list of all rational points on this curve.

Use very naive point enumeration to find all rational points on this curve over a finite field.

EXAMPLE:

sage: A, (x,y) = AffineSpace(2,GF(9,'a')).objgens()
sage: C = Curve(x^2 + y^2 - 1)
sage: C
Affine Curve over Finite Field in a of size 3^2 defined by x0^2 + x1^2 - 1
sage: C.rational_points()
[(0, 1), (0, 2), (1, 0), (2, 0), (a + 1, a + 1), (a + 1, 2*a + 2), (2*a + 2, a + 1), (2*a + 2, 2*a + 2)]

class sage.schemes.plane_curves.affine_curve.AffineCurve_generic(A, f)

Bases: sage.schemes.plane_curves.curve.Curve_generic

divisor_of_function(r)

Return the divisor of a function on a curve.

INPUT: r is a rational function on X

OUTPUT:

• list - The divisor of r represented as a list of coefficients and points. (TODO: This will change to a more structural output in the future.)

EXAMPLES:

sage: F = GF(5)
sage: P2 = AffineSpace(2, F, names = 'xy')
sage: R = P2.coordinate_ring()
sage: x, y = R.gens()
sage: f = y^2 - x^9 - x
sage: C = Curve(f)
sage: K = FractionField(R)
sage: r = 1/x
sage: C.divisor_of_function(r)     # todo: not implemented (broken)
      [[-1, (0, 0, 1)]]
sage: r = 1/x^3
sage: C.divisor_of_function(r)     # todo: not implemented (broken)
      [[-3, (0, 0, 1)]]

local_coordinates(pt, n)

Return local coordinates to precision n at the given point.

Behaviour is flaky - some choices of are worst that others.

INPUT:

• pt - an F-rational point on X which is not a point of ramification for the projection (x,y) - x.
• n - the number of terms desired

OUTPUT: x = x0 + t y = y0 + power series in t

EXAMPLES:

sage: F = GF(5)
sage: pt = (2,3)
sage: R = PolynomialRing(F,2, names = ['x','y'])
sage: x,y = R.gens()
sage: f = y^2-x^9-x
sage: C = Curve(f)
sage: C.local_coordinates(pt, 9)
[t + 2, -2*t^12 - 2*t^11 + 2*t^9 + t^8 - 2*t^7 - 2*t^6 - 2*t^4 + t^3 - 2*t^2 - 2]

plot(*args, **kwds)

Plot the real points on this affine plane curve.

INPUT:

• self - an affine plane curve
• *args - optional tuples (variable, minimum, maximum) for plotting dimensions
• **kwds - optional keyword arguments passed on to implicit_plot

EXAMPLES:

A cuspidal curve:

sage: R.<x, y> = QQ[]
sage: C = Curve(x^3 - y^2)
sage: C.plot()

A 5-nodal curve of degree 11. This example also illustrates some of the optional arguments:

sage: R.<x, y> = ZZ[]
sage: C = Curve(32*x^2 - 2097152*y^11 + 1441792*y^9 - 360448*y^7 + 39424*y^5 - 1760*y^3 + 22*y - 1)
sage: C.plot((x, -1, 1), (y, -1, 1), plot_points=400)

A line over :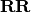

sage: R.<x, y> = RR[]
sage: C = Curve(R(y - sqrt(2)*x))
sage: C.plot()

class sage.schemes.plane_curves.affine_curve.AffineCurve_prime_finite_field(A, f)

Bases: sage.schemes.plane_curves.affine_curve.AffineCurve_finite_field

rational_points(algorithm='enum')

Return sorted list of all rational points on this curve.

INPUT:

• algorithm - string:
  • 'enum' - straightforward enumeration
  • 'bn' - via Singular’s Brill-Noether package.
  • 'all' - use all implemented algorithms and verify that they give the same answer, then return it

Note

The Brill-Noether package does not always work. When it fails a RuntimeError exception is raised.

EXAMPLE:

sage: x, y = (GF(5)['x,y']).gens()
sage: f = y^2 - x^9 - x
sage: C = Curve(f); C
Affine Curve over Finite Field of size 5 defined by -x^9 + y^2 - x
sage: C.rational_points(algorithm='bn')
[(0, 0), (2, 2), (2, 3), (3, 1), (3, 4)]
sage: C = Curve(x - y + 1)
sage: C.rational_points()
[(0, 1), (1, 2), (2, 3), (3, 4), (4, 0)]

We compare Brill-Noether and enumeration:

sage: x, y = (GF(17)['x,y']).gens()
sage: C = Curve(x^2 + y^5 + x*y - 19)
sage: v = C.rational_points(algorithm='bn')
sage: w = C.rational_points(algorithm='enum')
sage: len(v)
20
sage: v == w
True

riemann_roch_basis(D)

Interfaces with Singular’s BrillNoether command.

INPUT:

• self - a plane curve defined by a polynomial eqn f(x,y) = 0 over a prime finite field F = GF(p) in 2 variables x,y representing a curve X: f(x,y) = 0 having n F-rational points (see the Sage function places_on_curve)
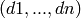• D - an n-tuple of integers representing the divisor 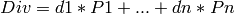, where 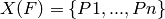. The ordering is that dictated by places_on_curve.

OUTPUT: basis of L(Div)

EXAMPLE:

sage: R = PolynomialRing(GF(5),2,names = ["x","y"])
sage: x, y = R.gens()
sage: f = y^2 - x^9 - x
sage: C = Curve(f)
sage: D = [6,0,0,0,0,0]
sage: C.riemann_roch_basis(D)
[1, (y^2*z^4 - x*z^5)/x^6, (y^2*z^5 - x*z^6)/x^7, (y^2*z^6 - x*z^7)/x^8]

class sage.schemes.plane_curves.affine_curve.AffineSpaceCurve_generic(A, X)

Bases: sage.schemes.plane_curves.curve.Curve_generic, sage.schemes.generic.algebraic_scheme.AlgebraicScheme_subscheme_affine