An algebraic scheme must be defined by sets of equations in affine or projective spaces, perhaps by means of gluing relations.
Bases: sage.schemes.generic.scheme.Scheme
An algebraic scheme presented as a subscheme in an ambient space.
Return the ambient space of this algebraic scheme.
EXAMPLES:
sage: A.<x, y> = AffineSpace(2, GF(5))
sage: S = A.subscheme([])
sage: S.ambient_space()
Affine Space of dimension 2 over Finite Field of size 5
sage: P.<x, y, z> = ProjectiveSpace(2, ZZ)
sage: S = P.subscheme([x-y, x-z])
sage: S.ambient_space() is P
True
Return the coordinate ring of this algebraic scheme. The result is cached.
EXAMPLES:
sage: P.<x, y, z> = ProjectiveSpace(2, ZZ)
sage: S = P.subscheme([x-y, x-z])
sage: S.coordinate_ring()
Quotient of Multivariate Polynomial Ring in x, y, z over Integer Ring by the ideal (x - y, x - z)
Return True if self is presented as a subscheme of an ambient projective space.
EXAMPLES:
sage: PP.<x,y,z,w> = ProjectiveSpace(3,QQ)
sage: f = x^3 + y^3 + z^3 + w^3
sage: R = f.parent()
sage: I = [f] + [f.derivative(zz) for zz in PP.gens()]
sage: V = PP.subscheme(I)
sage: V.is_projective()
True
sage: AA.<x,y,z,w> = AffineSpace(4,QQ)
sage: V = AA.subscheme(I)
sage: V.is_projective()
False
Return the number of generators of the ambient space of this algebraic scheme.
EXAMPLES:
sage: A.<x, y> = AffineSpace(2, GF(5))
sage: S = A.subscheme([])
sage: S.ngens()
2
sage: P.<x, y, z> = ProjectiveSpace(2, ZZ)
sage: S = P.subscheme([x-y, x-z])
sage: P.ngens()
3
Bases: sage.schemes.generic.algebraic_scheme.AlgebraicScheme
The quasi-affine or quasi-projective scheme 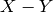 , where
, where  and
and 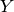 are both closed subschemes of a common ambient affine or projective
space.
are both closed subschemes of a common ambient affine or projective
space.
Return the scheme  such that self is represented as
such that self is represented as 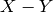 .
.
EXAMPLES:
sage: P.<x, y, z> = ProjectiveSpace(2, ZZ)
sage: S = P.subscheme([])
sage: T = P.subscheme([x-y])
sage: U = T.complement(S)
sage: U.X() is S
True
Return the scheme 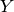 such that self is represented as
such that self is represented as 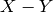 .
.
EXAMPLES:
sage: P.<x, y, z> = ProjectiveSpace(2, ZZ)
sage: S = P.subscheme([])
sage: T = P.subscheme([x-y])
sage: U = T.complement(S)
sage: U.Y() is T
True
Return the set of rational points on this algebraic scheme
over the field  .
.
EXAMPLES:
sage: A.<x, y> = AffineSpace(2, GF(7))
sage: S = A.subscheme([x^2-y])
sage: T = A.subscheme([x-y])
sage: U = T.complement(S)
sage: U.rational_points()
[(2, 4), (3, 2), (4, 2), (5, 4), (6, 1)]
sage: U.rational_points(GF(7^2, 'b'))
[(2, 4), (3, 2), (4, 2), (5, 4), (6, 1), (b, b + 4), (b + 1, 3*b + 5), (b + 2, 5*b + 1),
(b + 3, 6), (b + 4, 2*b + 6), (b + 5, 4*b + 1), (b + 6, 6*b + 5), (2*b, 4*b + 2),
(2*b + 1, b + 3), (2*b + 2, 5*b + 6), (2*b + 3, 2*b + 4), (2*b + 4, 6*b + 4),
(2*b + 5, 3*b + 6), (2*b + 6, 3), (3*b, 2*b + 1), (3*b + 1, b + 2), (3*b + 2, 5),
(3*b + 3, 6*b + 3), (3*b + 4, 5*b + 3), (3*b + 5, 4*b + 5), (3*b + 6, 3*b + 2),
(4*b, 2*b + 1), (4*b + 1, 3*b + 2), (4*b + 2, 4*b + 5), (4*b + 3, 5*b + 3),
(4*b + 4, 6*b + 3), (4*b + 5, 5), (4*b + 6, b + 2), (5*b, 4*b + 2), (5*b + 1, 3),
(5*b + 2, 3*b + 6), (5*b + 3, 6*b + 4), (5*b + 4, 2*b + 4), (5*b + 5, 5*b + 6),
(5*b + 6, b + 3), (6*b, b + 4), (6*b + 1, 6*b + 5), (6*b + 2, 4*b + 1), (6*b + 3, 2*b + 6),
(6*b + 4, 6), (6*b + 5, 5*b + 1), (6*b + 6, 3*b + 5)]
Bases: sage.schemes.generic.algebraic_scheme.AlgebraicScheme
An algebraic scheme presented as a closed subscheme is defined by explicit polynomial equations. This is as opposed to a general scheme, which could, e.g., be the Neron model of some object, and for which we do not want to give explicit equations.
INPUT:
A - ambient space (e.g. affine or projective  -space)
-space)
polynomials; in any case polynomials must belong to the coordinate ring of the ambient space and define valid polynomial functions (e.g. they should be homogeneous in the case of a projective space)
OUTPUT:
EXAMPLES:
sage: from sage.schemes.generic.algebraic_scheme import AlgebraicScheme_subscheme
sage: P.<x, y, z> = ProjectiveSpace(2, QQ)
sage: P.subscheme([x^2-y*z])
Closed subscheme of Projective Space of dimension 2 over Rational Field defined by:
x^2 - y*z
sage: AlgebraicScheme_subscheme(P, [x^2-y*z])
Closed subscheme of Projective Space of dimension 2 over Rational Field defined by:
x^2 - y*z
Return the base change to the ring 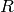 of this scheme.
of this scheme.
EXAMPLES:
sage: P.<x, y, z> = ProjectiveSpace(2, GF(11))
sage: S = P.subscheme([x^2-y*z])
sage: S.base_extend(GF(11^2, 'b'))
Closed subscheme of Projective Space of dimension 2 over Finite Field in b of size 11^2 defined by:
x^2 - y*z
sage: S.base_extend(ZZ)
...
ValueError: no natural map from the base ring (=Finite Field of size 11) to R (=Integer Ring)!
Return the scheme-theoretic complement other - self, where self and other are both closed algebraic subschemes of the same ambient space.
If other is unspecified, it is taken to be the ambient space of self.
EXAMPLES:
sage: A.<x, y, z> = AffineSpace(3, ZZ)
sage: X = A.subscheme([x+y-z])
sage: Y = A.subscheme([x-y+z])
sage: Y.complement(X)
Quasi-affine subscheme X - Y of Affine Space of dimension 3 over Integer Ring, where X is defined by:
x + y - z
and Y is defined by:
x - y + z
sage: Y.complement()
Quasi-affine subscheme X - Y of Affine Space of dimension 3 over Integer Ring, where X is defined by:
(no polynomials)
and Y is defined by:
x - y + z
sage: P.<x, y, z> = ProjectiveSpace(2, QQ)
sage: X = P.subscheme([x^2+y^2+z^2])
sage: Y = P.subscheme([x*y+y*z+z*x])
sage: Y.complement(X)
Quasi-projective subscheme X - Y of Projective Space of dimension 2 over Rational Field, where X is defined by:
x^2 + y^2 + z^2
and Y is defined by:
x*y + x*z + y*z
sage: Y.complement(P)
Quasi-projective subscheme X - Y of Projective Space of dimension 2 over Rational Field, where X is defined by:
(no polynomials)
and Y is defined by:
x*y + x*z + y*z
Return the ideal that defines this scheme as a subscheme of its ambient space.
EXAMPLES:
sage: P.<x, y, z> = ProjectiveSpace(2, ZZ)
sage: S = P.subscheme([x^2-y*z, x^3+z^3])
sage: S.defining_ideal()
Ideal (x^2 - y*z, x^3 + z^3) of Multivariate Polynomial Ring in x, y, z over Integer Ring
Return the polynomials that define this scheme as a subscheme of its ambient space.
EXAMPLES:
sage: P.<x, y, z> = ProjectiveSpace(2, ZZ)
sage: S = P.subscheme([x^2-y*z, x^3+z^3])
sage: S.defining_polynomials()
(x^2 - y*z, x^3 + z^3)
Return the scheme-theoretic intersection of self and other in their common ambient space.
EXAMPLES:
sage: A.<x, y> = AffineSpace(2, ZZ)
sage: X = A.subscheme([x^2-y])
sage: Y = A.subscheme([y])
sage: X.intersection(Y)
Closed subscheme of Affine Space of dimension 2 over Integer Ring defined by:
x^2 - y,
y
Return the irreducible components of this algebraic scheme, as subschemes of the same ambient space.
OUTPUT: an immutable sequence of irreducible subschemes of the ambient space of this scheme
The components are cached.
EXAMPLES:
We define what is clearly a union of four hypersurfaces in
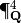 then find the irreducible components.
then find the irreducible components.
sage: PP.<x,y,z,w,v> = ProjectiveSpace(4,QQ)
sage: V = PP.subscheme( (x^2 - y^2 - z^2)*(w^5 - 2*v^2*z^3)* w * (v^3 - x^2*z) )
sage: V.irreducible_components()
[
Closed subscheme of Projective Space of dimension 4 over Rational Field defined by:
w,
Closed subscheme of Projective Space of dimension 4 over Rational Field defined by:
x^2 - y^2 - z^2,
Closed subscheme of Projective Space of dimension 4 over Rational Field defined by:
x^2*z - v^3,
Closed subscheme of Projective Space of dimension 4 over Rational Field defined by:
w^5 - 2*z^3*v^2
]
We verify that the irrelevant ideal isn’t accidently returned (see trac 6920):
sage: PP.<x,y,z,w> = ProjectiveSpace(3,QQ)
sage: f = x^3 + y^3 + z^3 + w^3
sage: R = f.parent()
sage: I = [f] + [f.derivative(zz) for zz in PP.gens()]
sage: V = PP.subscheme(I)
sage: V.irreducible_components()
[
<BLANKLINE>
]
The same polynomial as above defines a scheme with a nontrivial irreducible component in affine space (instead of the empty scheme as above):
sage: AA.<x,y,z,w> = AffineSpace(4,QQ)
sage: V = AA.subscheme(I)
sage: V.irreducible_components()
[
Closed subscheme of Affine Space of dimension 4 over Rational Field defined by:
w,
z,
y,
x
]
EXAMPLES:
One can enumerate points up to a given bound on a projective scheme over the rationals.
sage: E = EllipticCurve('37a')
sage: E.rational_points(bound=8)
[(0 : 0 : 1),
(1 : 0 : 1),
(-1 : 0 : 1),
(0 : -1 : 1),
(1 : -1 : 1),
(-1 : -1 : 1),
(2 : 2 : 1),
(2 : -3 : 1),
(1/4 : -3/8 : 1),
(1/4 : -5/8 : 1),
(0 : 1 : 0)]
For a small finite field, the complete set of points can be enumerated.
sage: Etilde = E.base_extend(GF(3))
sage: Etilde.rational_points()
[(0 : 0 : 1), (0 : 1 : 0), (0 : 2 : 1), (1 : 0 : 1), (1 : 2 : 1), (2 : 0 : 1), (2 : 2 : 1)]
The class of hyperelliptic curves does not (yet) support desingularization of the places at infinity into two points.
sage: FF = FiniteField(7)
sage: P.<x> = PolynomialRing(FiniteField(7))
sage: C = HyperellipticCurve(x^8+x+1)
sage: C.rational_points()
[(2 : 0 : 1), (4 : 0 : 1), (0 : 1 : 1), (6 : 1 : 1), (0 : 6 : 1), (6 : 6 : 1), (0 : 1 : 0)]
TODO:
Return the corresponding reduced algebraic space associated to this scheme.
EXAMPLES: First we construct the union of a doubled and tripled
line in the affine plane over 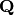 .
.
sage: A.<x,y> = AffineSpace(2, QQ)
sage: X = A.subscheme([(x-1)^2*(x-y)^3]); X
Closed subscheme of Affine Space of dimension 2 over Rational Field defined by:
x^5 - 3*x^4*y + 3*x^3*y^2 - x^2*y^3 - 2*x^4 + 6*x^3*y - 6*x^2*y^2 + 2*x*y^3 + x^3 - 3*x^2*y + 3*x*y^2 - y^3
sage: X.dimension()
1
Then we compute the corresponding reduced scheme.
sage: Y = X.reduce(); Y
Closed subscheme of Affine Space of dimension 2 over Rational Field defined by:
x^2 - x*y - x + y
Finally, we verify that the reduced scheme 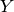 is the union
of those two lines.
is the union
of those two lines.
sage: L1 = A.subscheme([x-1]); L1
Closed subscheme of Affine Space of dimension 2 over Rational Field defined by:
x - 1
sage: L2 = A.subscheme([x-y]); L2
Closed subscheme of Affine Space of dimension 2 over Rational Field defined by:
x - y
sage: W = L1.union(L2); W # taken in ambient space
Closed subscheme of Affine Space of dimension 2 over Rational Field defined by:
x^2 - x*y - x + y
sage: Y == W
True
Return the scheme-theoretic union of self and other in their common ambient space.
EXAMPLES: We construct the union of a line and a tripled-point on the line.
sage: A.<x,y> = AffineSpace(2, QQ)
sage: I = ideal([x,y])^3
sage: P = A.subscheme(I)
sage: L = A.subscheme([y-1])
sage: S = L.union(P); S
Closed subscheme of Affine Space of dimension 2 over Rational Field defined by:
y^4 - y^3,
x*y^3 - x*y^2,
x^2*y^2 - x^2*y,
x^3*y - x^3
sage: S.dimension()
1
sage: S.reduce()
Closed subscheme of Affine Space of dimension 2 over Rational Field defined by:
y^2 - y,
x*y - x
We can also use the notation “+” for the union:
sage: A.subscheme([x]) + A.subscheme([y^2 - (x^3+1)])
Closed subscheme of Affine Space of dimension 2 over Rational Field defined by:
-x^4 + x*y^2 - x
Saving and loading:
sage: loads(S.dumps()) == S
True
Bases: sage.schemes.generic.algebraic_scheme.AlgebraicScheme_subscheme
EXAMPLES:
sage: A.<x,y> = AffineSpace(2, QQ)
sage: A.subscheme([]).dimension()
2
sage: A.subscheme([x]).dimension()
1
sage: A.subscheme([x^5]).dimension()
1
sage: A.subscheme([x^2 + y^2 - 1]).dimension()
1
sage: A.subscheme([x*(x-1), y*(y-1)]).dimension()
0
Something less obvious
sage: A.<x,y,z,w> = AffineSpace(4, QQ)
sage: X = A.subscheme([x^2, x^2*y^2 + z^2, z^2 - w^2, 10*x^2 + w^2 - z^2])
sage: X
Closed subscheme of Affine Space of dimension 4 over Rational Field defined by:
x^2,
x^2*y^2 + z^2,
z^2 - w^2,
10*x^2 - z^2 + w^2
sage: X.dimension()
1
Returns a morphism from this affine scheme into an ambient projective space of the same dimension.
INPUT:
EXAMPLES:
sage: A.<x, y, z> = AffineSpace(3, ZZ)
sage: S = A.subscheme([x*y-z])
sage: S.projective_embedding()
Scheme morphism:
From: Closed subscheme of Affine Space of dimension 3 over Integer Ring defined by:
x*y - z
To: Closed subscheme of Projective Space of dimension 3 over Integer Ring defined by:
x0*x1 - x2*x3
Defn: Defined on coordinates by sending (x, y, z) to
(xbar : ybar : zbar : 1)
Bases: sage.schemes.generic.algebraic_scheme.AlgebraicScheme_subscheme
Return the 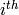 affine patch of this projective scheme.
This is the intersection with this
affine patch of this projective scheme.
This is the intersection with this 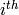 affine patch of
its ambient space.
affine patch of
its ambient space.
INPUT:
OUTPUT: an affine scheme with fixed projective_embedding map.
EXAMPLES:
sage: PP = ProjectiveSpace(2, QQ, names='X,Y,Z')
sage: X,Y,Z = PP.gens()
sage: C = PP.subscheme(X^3*Y + Y^3*Z + Z^3*X)
sage: U = C.affine_patch(0)
sage: U
Closed subscheme of Affine Space of dimension 2 over Rational Field defined by:
x0^3*x1 + x1^3 + x0
sage: U.projective_embedding()
Scheme morphism:
From: Closed subscheme of Affine Space of dimension 2 over Rational Field defined by:
x0^3*x1 + x1^3 + x0
To: Closed subscheme of Projective Space of dimension 2 over Rational Field defined by:
X^3*Y + Y^3*Z + X*Z^3
Defn: Defined on coordinates by sending (x0, x1) to
(1 : x0bar : x1bar)
EXAMPLES:
sage: A.<x,y> = AffineSpace(2, QQ)
sage: A.subscheme([]).dimension()
2
sage: A.subscheme([x]).dimension()
1
sage: A.subscheme([x^5]).dimension()
1
sage: A.subscheme([x^2 + y^2 - 1]).dimension()
1
sage: A.subscheme([x*(x-1), y*(y-1)]).dimension()
0
Something less obvious
sage: A.<x,y,z,w> = AffineSpace(4, QQ)
sage: X = A.subscheme([x^2, x^2*y^2 + z^2, z^2 - w^2, 10*x^2 + w^2 - z^2])
sage: X
Closed subscheme of Affine Space of dimension 4 over Rational Field defined by:
x^2,
x^2*y^2 + z^2,
z^2 - w^2,
10*x^2 - z^2 + w^2
sage: X.dimension()
1
Return True if 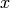 is an algebraic scheme, i.e., a
subscheme of an ambient space over a ring defined by polynomial
equations.
is an algebraic scheme, i.e., a
subscheme of an ambient space over a ring defined by polynomial
equations.
EXAMPLES: Affine space is itself not an algebraic scheme, though the closed subscheme defined by no equations is.
sage: from sage.schemes.generic.algebraic_scheme import is_AlgebraicScheme
sage: is_AlgebraicScheme(AffineSpace(10, QQ))
False
sage: V = AffineSpace(10, QQ).subscheme([]); V
Closed subscheme of Affine Space of dimension 10 over Rational Field defined by:
(no polynomials)
sage: is_AlgebraicScheme(V)
True
We create a more complicated closed subscheme.
sage: A, x = AffineSpace(10, QQ).objgens()
sage: X = A.subscheme([sum(x)]); X
Closed subscheme of Affine Space of dimension 10 over Rational Field defined by:
x0 + x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9
sage: is_AlgebraicScheme(X)
True
sage: is_AlgebraicScheme(QQ)
False
sage: S = Spec(QQ)
sage: is_AlgebraicScheme(S)
False