AUTHORS:
Return the plane or space curve defined by 
, where
can be either a multivariate polynomial, a list or
tuple of polynomials, or an algebraic scheme.
If is in two variables the curve is affine, and if it
is homogenous in 
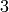variables, then the curve is
projective.
EXAMPLE: A projective plane curve
sage: x,y,z = QQ['x,y,z'].gens()
sage: C = Curve(x^3 + y^3 + z^3); C
Projective Curve over Rational Field defined by x^3 + y^3 + z^3
sage: C.genus()
1
EXAMPLE: Affine plane curves
sage: x,y = GF(7)['x,y'].gens()
sage: C = Curve(y^2 + x^3 + x^10); C
Affine Curve over Finite Field of size 7 defined by x^10 + x^3 + y^2
sage: C.genus()
0
sage: x, y = QQ['x,y'].gens()
sage: Curve(x^3 + y^3 + 1)
Affine Curve over Rational Field defined by x^3 + y^3 + 1
EXAMPLE: A projective space curve
sage: x,y,z,w = QQ['x,y,z,w'].gens()
sage: C = Curve([x^3 + y^3 - z^3 - w^3, x^5 - y*z^4]); C
Projective Space Curve over Rational Field defined by x^3 + y^3 - z^3 - w^3
sage: C.genus()
13
EXAMPLE: An affine space curve
sage: x,y,z = QQ['x,y,z'].gens()
sage: C = Curve([y^2 + x^3 + x^10 + z^7, x^2 + y^2]); C
Affine Space Curve over Rational Field defined by x^10 + z^7 + x^3 + y^2
sage: C.genus()
47
EXAMPLE: We can also make non-reduced non-irreducible curves.
sage: x,y,z = QQ['x,y,z'].gens()
sage: Curve((x-y)*(x+y))
Projective Curve over Rational Field defined by x^2 - y^2
sage: Curve((x-y)^2*(x+y)^2)
Projective Curve over Rational Field defined by x^4 - 2*x^2*y^2 + y^4
EXAMPLE: A union of curves is a curve.
sage: x,y,z = QQ['x,y,z'].gens()
sage: C = Curve(x^3 + y^3 + z^3)
sage: D = Curve(x^4 + y^4 + z^4)
sage: C.union(D)
Projective Curve over Rational Field defined by
x^7 + x^4*y^3 + x^3*y^4 + y^7 + x^4*z^3 + y^4*z^3 + x^3*z^4 + y^3*z^4 + z^7
The intersection is not a curve, though it is a scheme.
sage: X = C.intersection(D); X
Closed subscheme of Projective Space of dimension 2 over Rational Field defined by:
x^3 + y^3 + z^3,
x^4 + y^4 + z^4
Note that the intersection has dimension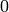 
.
sage: X.dimension()
0
sage: I = X.defining_ideal(); I
Ideal (x^3 + y^3 + z^3, x^4 + y^4 + z^4) of Multivariate Polynomial Ring in x, y, z over Rational Field
EXAMPLE: In three variables, the defining equation must be homogeneous.
If the parent polynomial ring is in three variables, then the defining ideal must be homogeneous.
sage: x,y,z = QQ['x,y,z'].gens()
sage: Curve(x^2+y^2)
Projective Curve over Rational Field defined by x^2 + y^2
sage: Curve(x^2+y^2+z)
...
TypeError: x^2 + y^2 + z is not a homogeneous polynomial!
The defining polynomial must always be nonzero:
sage: P1.<x,y> = ProjectiveSpace(1,GF(5))
sage: Curve(0*x)
...
ValueError: defining polynomial of curve must be nonzero