AUTHORS:
Return the Hasse-Weil bounds for the cardinality of a nonsingular
curve defined over 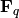 of given genus.
of given genus.
INPUT:
OUTPUT:
(tuple) The Hasse bounds (lb,ub) for the cardinality of a curve of
genus genus defined over 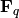 .
.
EXAMPLES:
sage: Hasse_bounds(2)
(1, 5)
sage: Hasse_bounds(next_prime(10^30))
(999999999999998000000000000058, 1000000000000002000000000000058)
Bases: sage.schemes.plane_curves.projective_curve.ProjectiveCurve_generic
Return the rational points on this curve computed via enumeration.
INPUT:
OUTPUT:
A list of all the rational points on the curve defined over its base field, possibly sorted.
Note
This is a slow Python-level implementation.
EXAMPLES:
sage: F = GF(7)
sage: P2.<X,Y,Z> = ProjectiveSpace(F,2)
sage: C = Curve(X^3+Y^3-Z^3)
sage: C.rational_points()
[(0 : 1 : 1), (0 : 2 : 1), (0 : 4 : 1), (1 : 0 : 1), (2 : 0 : 1), (3 : 1 : 0), (4 : 0 : 1), (5 : 1 : 0), (6 : 1 : 0)]
sage: F = GF(1237)
sage: P2.<X,Y,Z> = ProjectiveSpace(F,2)
sage: C = Curve(X^7+7*Y^6*Z+Z^4*X^2*Y*89)
sage: len(C.rational_points())
1237
sage: F = GF(2^6,'a')
sage: P2.<X,Y,Z> = ProjectiveSpace(F,2)
sage: C = Curve(X^5+11*X*Y*Z^3 + X^2*Y^3 - 13*Y^2*Z^3)
sage: len(C.rational_points())
104
sage: R.<x,y,z> = GF(2)[]
sage: f = x^3*y + y^3*z + x*z^3
sage: C = Curve(f); pts = C.rational_points()
sage: pts
[(0 : 0 : 1), (0 : 1 : 0), (1 : 0 : 0)]
Return a generator object for the rational points on this curve.
INPUT:
OUTPUT:
A generator of all the rational points on the curve defined over its base field.
EXAMPLE:
sage: F = GF(37)
sage: P2.<X,Y,Z> = ProjectiveSpace(F,2)
sage: C = Curve(X^7+Y*X*Z^5*55+Y^7*12)
sage: len(list(C.rational_points_iterator()))
37
sage: F = GF(2)
sage: P2.<X,Y,Z> = ProjectiveSpace(F,2)
sage: C = Curve(X*Y*Z)
sage: a = C.rational_points_iterator()
sage: a.next()
(1 : 0 : 0)
sage: a.next()
(0 : 1 : 0)
sage: a.next()
(1 : 1 : 0)
sage: a.next()
(0 : 0 : 1)
sage: a.next()
(1 : 0 : 1)
sage: a.next()
(0 : 1 : 1)
sage: a.next()
...
StopIteration
sage: F = GF(3^2,'a')
sage: P2.<X,Y,Z> = ProjectiveSpace(F,2)
sage: C = Curve(X^3+5*Y^2*Z-33*X*Y*X)
sage: b = C.rational_points_iterator()
sage: b.next()
(0 : 1 : 0)
sage: b.next()
(0 : 0 : 1)
sage: b.next()
(2*a + 2 : 2*a : 1)
sage: b.next()
(2 : a + 1 : 1)
sage: b.next()
(a + 1 : a + 2 : 1)
sage: b.next()
(1 : 2 : 1)
sage: b.next()
(2*a + 2 : a : 1)
sage: b.next()
(2 : 2*a + 2 : 1)
sage: b.next()
(a + 1 : 2*a + 1 : 1)
sage: b.next()
(1 : 1 : 1)
sage: b.next()
...
StopIteration
Bases: sage.schemes.plane_curves.curve.Curve_generic_projective
Return the arithmetic genus of this curve.
This is the arithmetic genus 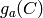 as defined in
Hartshorne. If the curve has degree
as defined in
Hartshorne. If the curve has degree  then this is simply
then this is simply
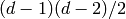 . It need not equal the geometric genus
(the genus of the normalization of the curve).
. It need not equal the geometric genus
(the genus of the normalization of the curve).
EXAMPLE:
sage: x,y,z = PolynomialRing(GF(5), 3, 'xyz').gens()
sage: C = Curve(y^2*z^7 - x^9 - x*z^8); C
Projective Curve over Finite Field of size 5 defined by -x^9 + y^2*z^7 - x*z^8
sage: C.arithmetic_genus()
28
sage: C.genus()
4
Return the divisor of a function on a curve.
INPUT: r is a rational function on X
OUTPUT:
EXAMPLES:
sage: FF = FiniteField(5)
sage: P2 = ProjectiveSpace(2, FF, names = ['x','y','z'])
sage: R = P2.coordinate_ring()
sage: x, y, z = R.gens()
sage: f = y^2*z^7 - x^9 - x*z^8
sage: C = Curve(f)
sage: K = FractionField(R)
sage: r = 1/x
sage: C.divisor_of_function(r) # todo: not implemented !!!!
[[-1, (0, 0, 1)]]
sage: r = 1/x^3
sage: C.divisor_of_function(r) # todo: not implemented !!!!
[[-3, (0, 0, 1)]]
Returns whether the curve is singular or not.
EXAMPLES:
Over  :
:
sage: F = QQ
sage: P2.<X,Y,Z> = ProjectiveSpace(F,2)
sage: C = Curve(X^3-Y^2*Z)
sage: C.is_singular()
True
Over a finite field:
sage: F = GF(19)
sage: P2.<X,Y,Z> = ProjectiveSpace(F,2)
sage: C = Curve(X^3+Y^3+Z^3)
sage: C.is_singular()
False
sage: D = Curve(X^4-X*Z^3)
sage: D.is_singular()
True
sage: E = Curve(X^5+19*Y^5+Z^5)
sage: E.is_singular()
True
sage: E = Curve(X^5+9*Y^5+Z^5)
sage: E.is_singular()
False
Over 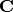 :
:
sage: F = CC
sage: P2.<X,Y,Z> = ProjectiveSpace(F,2)
sage: C = Curve(X)
sage: C.is_singular()
False
sage: D = Curve(Y^2*Z-X^3)
sage: D.is_singular()
True
sage: E = Curve(Y^2*Z-X^3+Z^3)
sage: E.is_singular()
False
Return local coordinates to precision n at the given point.
Behaviour is flaky - some choices ofare worst that others.
INPUT:
OUTPUT: x = x0 + t y = y0 + power series in t
EXAMPLES:
sage: FF = FiniteField(5)
sage: P2 = ProjectiveSpace(2, FF, names = ['x','y','z'])
sage: x, y, z = P2.coordinate_ring().gens()
sage: C = Curve(y^2*z^7-x^9-x*z^8)
sage: pt = C([2,3,1])
sage: C.local_coordinates(pt,9) # todo: not implemented !!!!
[2 + t, 3 + 3*t^2 + t^3 + 3*t^4 + 3*t^6 + 3*t^7 + t^8 + 2*t^9 + 3*t^11 + 3*t^12]
Plot the real points of an affine patch of this projective plane curve.
INPUT:
EXAMPLES:
A cuspidal curve:
sage: R.<x, y, z> = QQ[]
sage: C = Curve(x^3 - y^2*z)
sage: C.plot()
The other affine patches of the same curve:
sage: C.plot(patch=0)
sage: C.plot(patch=1)
An elliptic curve:
sage: E = EllipticCurve('101a')
sage: C = Curve(E)
sage: C.plot()
sage: C.plot(patch=0)
sage: C.plot(patch=1)
A hyperelliptic curve:
sage: P.<x> = QQ[]
sage: f = 4*x^5 - 30*x^3 + 45*x - 22
sage: C = HyperellipticCurve(f)
sage: C.plot()
sage: C.plot(patch=0)
sage: C.plot(patch=1)
Bases: sage.schemes.plane_curves.projective_curve.ProjectiveCurve_finite_field
INPUT:
EXAMPLE:
sage: x, y, z = PolynomialRing(GF(5), 3, 'xyz').gens()
sage: f = y^2*z^7 - x^9 - x*z^8
sage: C = Curve(f); C
Projective Curve over Finite Field of size 5 defined by -x^9 + y^2*z^7 - x*z^8
sage: C.rational_points()
[(0 : 0 : 1), (0 : 1 : 0), (2 : 2 : 1), (2 : 3 : 1), (3 : 1 : 1), (3 : 4 : 1)]
sage: C = Curve(x - y + z)
sage: C.rational_points()
[(0 : 1 : 1), (1 : 1 : 0), (1 : 2 : 1), (2 : 3 : 1), (3 : 4 : 1), (4 : 0 : 1)]
Note
The Brill-Noether package does not always work (i.e., the ‘bn’ algorithm. When it fails a RuntimeError exception is raised.
Return a basis for the Riemann-Roch space corresponding to
 .
.
Warning
This function calls a Singular function that appears to be very buggy and should not be trusted.
This uses Singular’s Brill-Noether implementation.
INPUT:
EXAMPLE:
sage: R.<x,y,z> = GF(2)[]
sage: f = x^3*y + y^3*z + x*z^3
sage: C = Curve(f); pts = C.rational_points()
sage: D = C.divisor([ (4, pts[0]), (0,pts[1]), (4, pts[2]) ])
sage: C.riemann_roch_basis(D)
[x/y, 1, z/y, z^2/y^2, z/x, z^2/(x*y)]
The following example illustrates that the Riemann-Roch space function in Singular doesn’t not work correctly.
sage: R.<x,y,z> = GF(5)[]
sage: f = x^7 + y^7 + z^7
sage: C = Curve(f); pts = C.rational_points()
sage: D = C.divisor([ (3, pts[0]), (-1,pts[1]), (10, pts[5]) ])
sage: C.riemann_roch_basis(D) # output is random (!!!!)
[x/(y + x), (z + y)/(y + x)]
The answer has dimension 2 (confirmed via Magma). But it varies between 1 and quite large with Singular.