AUTHORS:
This is a binding for the MPFR arbitrary-precision floating point library.
We define a class RealField, where each instance of RealField specifies a field of floating-point numbers with a specified precision and rounding mode. Individual floating-point numbers are of class RealNumber.
In Sage (as in MPFR), floating-point numbers of precision
 are of the form
are of the form 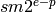 , where
, where
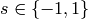 ,
, 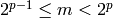 , and
, and
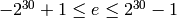 ; plus the special
values +0, -0,
+infinity, -infinity, and
NaN (which stands for Not-a-Number).
; plus the special
values +0, -0,
+infinity, -infinity, and
NaN (which stands for Not-a-Number).
Operations in this module which are direct wrappers of MPFR
functions are “correctly rounded”; we briefly describe what this
means. Assume that you could perform the operation exactly, on real
numbers, to get a result  . If this result can be
represented as a floating-point number, then we return that
number.
. If this result can be
represented as a floating-point number, then we return that
number.
Otherwise, the result  is between two floating-point
numbers. For the directed rounding modes (round to plus infinity,
round to minus infinity, round to zero), we return the
floating-point number in the indicated direction from
is between two floating-point
numbers. For the directed rounding modes (round to plus infinity,
round to minus infinity, round to zero), we return the
floating-point number in the indicated direction from  .
For round to nearest, we return the floating-point number which is
nearest to
.
For round to nearest, we return the floating-point number which is
nearest to  .
.
This leaves one case unspecified: in round to nearest mode, what
happens if  is exactly halfway between the two nearest
floating-point numbers? In that case, we round to the number with
an even mantissa (the mantissa is the number
is exactly halfway between the two nearest
floating-point numbers? In that case, we round to the number with
an even mantissa (the mantissa is the number  in the
representation above).
in the
representation above).
Consider the ordered set of floating-point numbers of precision
 . (Here we identify +0 and
-0, and ignore NaN.) We can give a
bijection between these floating-point numbers and a segment of the
integers, where 0 maps to 0 and adjacent floating-point numbers map
to adjacent integers. We call the integer corresponding to a given
floating-point number the “floating-point rank” of the number.
(This is not standard terminology; I just made it up.)
. (Here we identify +0 and
-0, and ignore NaN.) We can give a
bijection between these floating-point numbers and a segment of the
integers, where 0 maps to 0 and adjacent floating-point numbers map
to adjacent integers. We call the integer corresponding to a given
floating-point number the “floating-point rank” of the number.
(This is not standard terminology; I just made it up.)
EXAMPLES: A difficult conversion:
sage: RR(sys.maxint)
9.22337203685478e18 # 64-bit
2.14748364700000e9 # 32-bit
TESTS:
sage: -1e30
-1.00000000000000e30
Make sure we don’t have a new field for every new literal:
sage: parent(2.0) is parent(2.0)
True
sage: RealField(100, rnd='RNDZ') is RealField(100, rnd='RNDD')
False
sage: RealField(100, rnd='RNDZ') is RealField(100, rnd='RNDZ')
True
Bases: sage.categories.map.Map
EXAMPLES:
sage: from sage.rings.real_mpfr import RRtoRR
sage: R10 = RealField(10)
sage: R100 = RealField(100)
sage: f = RRtoRR(R100, R10)
sage: f.section()
Generic map:
From: Real Field with 10 bits of precision
To: Real Field with 100 bits of precision
RealField(prec, sci_not, rnd):
INPUT:
- ‘RNDN’ - (default) round to nearest (ties go to the even number): Knuth says this is the best choice to prevent “floating point drift”.
- ‘RNDD’ - round towards minus infinity
- ‘RNDZ’ - round towards zero
- ‘RNDU’ - round towards plus infinity
EXAMPLES:
sage: RealField(10)
Real Field with 10 bits of precision
sage: RealField()
Real Field with 53 bits of precision
sage: RealField(100000)
Real Field with 100000 bits of precision
Here we show the effect of rounding:
sage: R17d = RealField(17,rnd='RNDD')
sage: a = R17d(1)/R17d(3); a.exact_rational()
87381/262144
sage: R17u = RealField(17,rnd='RNDU')
sage: a = R17u(1)/R17u(3); a.exact_rational()
43691/131072
Note
The default precision is 53, since according to the MPFR manual: ‘mpfr should be able to exactly reproduce all computations with double-precision machine floating-point numbers (double type in C), except the default exponent range is much wider and subnormal numbers are not implemented.’
Bases: sage.rings.ring.Field
An approximation to the field of real numbers using floating point numbers with any specified precision. Answers derived from calculations in this approximation may differ from what they would be if those calculations were performed in the true field of real numbers. This is due to the rounding errors inherent to finite precision calculations.
See the documentation for the module sage.rings.real_mpfr for more details.
Returns the algebraic closure of self, i.e., the complex field with the same precision.
EXAMPLES:
sage: RR.algebraic_closure()
Complex Field with 53 bits of precision
sage: RR.algebraic_closure() is CC
True
sage: RealField(100,rnd='RNDD').algebraic_closure()
Complex Field with 100 bits of precision
sage: RealField(100).algebraic_closure()
Complex Field with 100 bits of precision
Returns Catalan’s constant to the precision of this field.
EXAMPLES:
sage: RealField(100).catalan_constant()
0.91596559417721901505460351493
Returns 0, since the field of real numbers has characteristic 0.
EXAMPLES:
sage: RealField(10).characteristic()
0
Return complex field of the same precision.
EXAMPLES:
sage: RR.complex_field()
Complex Field with 53 bits of precision
sage: RR.complex_field() is CC
True
sage: RealField(100,rnd='RNDD').complex_field()
Complex Field with 100 bits of precision
sage: RealField(100).complex_field()
Complex Field with 100 bits of precision
Returns the functorial construction of self, namely,
completion of the rational numbers with respect to the prime
at 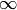 .
.
Also preserves other information that makes this field unique (e.g. precision, rounding, print mode).
EXAMPLES:
sage: R = RealField(100, rnd='RNDU')
sage: c, S = R.construction(); S
Rational Field
sage: R == c(S)
True
Returns Euler’s gamma constant to the precision of this field.
EXAMPLES:
sage: RealField(100).euler_constant()
0.57721566490153286060651209008
Return the factorial of the integer n as a real number.
EXAMPLES:
sage: RR.factorial(0)
1.00000000000000
sage: RR.factorial(1000000)
8.26393168833124e5565708
sage: RR.factorial(-1)
...
ArithmeticError: n must be nonnegative
Return the generators of self.
EXAMPLES:
sage: R=RealField(100)
sage: R.gen(0)
1.0000000000000000000000000000
sage: R.gen(1)
...
IndexError: self has only one generator
Return a list of generators.
EXAMPLE:
sage: RR.gens()
[1.00000000000000]
Returns True, to signify that elements of this field print without sums, so parenthesis aren’t required, e.g., in coefficients of polynomials.
EXAMPLES:
sage: RealField(10).is_atomic_repr()
True
Return False, since a real field (represented using finite precision) is not exact.
EXAMPLE:
sage: RR.is_exact()
False
sage: RealField(100).is_exact()
False
Returns False, since the field of real numbers is not finite.
EXAMPLES:
sage: RealField(10).is_finite()
False
Returns log(2) (i.e., the natural log of 2) to the precision of this field.
EXAMPLES:
sage: R=RealField(100)
sage: R.log2()
0.69314718055994530941723212146
sage: R(2).log()
0.69314718055994530941723212146
Returns the name of self, which encodes the precision and rounding convention.
EXAMPLES:
sage: RR.name()
'RealField53_0'
sage: RealField(100,rnd='RNDU').name()
'RealField100_2'
Return the number of generators.
EXAMPLES:
sage: RR.ngens()
1
Returns pi to the precision of this field.
EXAMPLES:
sage: R = RealField(100)
sage: R.pi()
3.1415926535897932384626433833
sage: R.pi().sqrt()/2
0.88622692545275801364908374167
sage: R = RealField(150)
sage: R.pi().sqrt()/2
0.88622692545275801364908374167057259139877473
Returns the precision of self.
EXAMPLES:
sage: RR.precision()
53
sage: RealField(20).precision()
20
Returns the precision of self.
EXAMPLES:
sage: RR.precision()
53
sage: RealField(20).precision()
20
Returns a uniformly distributed random number between min and max (default -1 to 1).
Warning
The argument distribution is ignored—the random number is from the uniform distribution.
EXAMPLES:
sage: RealField(100).random_element(-5, 10)
1.9305310520925994224072377281
sage: RealField(10).random_element()
-0.84
TESTS:
sage: RealField(31).random_element()
-0.207006278
sage: RealField(32).random_element()
-0.757827933
sage: RealField(33).random_element()
-0.530834221
sage: RealField(63).random_element()
0.918013195263849341
sage: RealField(64).random_element()
-0.805114150788947694
sage: RealField(65).random_element()
0.2035927570696802284
sage: RealField(10).random_element()
-0.59
sage: RealField(10).random_element()
0.57
sage: RR.random_element()
0.931242676441124
sage: RR.random_element()
0.979095507956490
Return the rounding mode.
EXAMPLES:
sage: RR.rounding_mode()
'RNDN'
sage: RealField(20,rnd='RNDZ').rounding_mode()
'RNDZ'
sage: RealField(20,rnd='RNDU').rounding_mode()
'RNDU'
sage: RealField(20,rnd='RNDD').rounding_mode()
'RNDD'
Set or return the scientific notation printing flag. If this flag is True then real numbers with this space as parent print using scientific notation.
INPUT:
Returns the real field that is identical to self, except that it has the specified precision.
EXAMPLES:
sage: RR.to_prec(212)
Real Field with 212 bits of precision
sage: R = RealField(30, rnd="RNDZ")
sage: R.to_prec(300)
Real Field with 300 bits of precision and rounding RNDZ
Return an  -th root of unity in the real field, if one
exists, or raise a ValueError otherwise.
-th root of unity in the real field, if one
exists, or raise a ValueError otherwise.
EXAMPLES:
sage: R = RealField()
sage: R.zeta()
-1.00000000000000
sage: R.zeta(1)
1.00000000000000
sage: R.zeta(5)
...
ValueError: No 5th root of unity in self
Bases: sage.rings.real_mpfr.RealNumber
Bases: sage.structure.element.RingElement
A floating point approximation to a real number using any specified precision. Answers derived from calculations with such approximations may differ from what they would be if those calculations were performed with true real numbers. This is due to the rounding errors inherent to finite precision calculations.
The approximation is printed to slightly fewer digits than its internal precision, in order to avoid confusing roundoff issues that occur because numbers are stored internally in binary.
Return the arithmetic-geometric mean of self and other. The
arithmetic-geometric mean is the common limit of the sequences
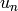 and
and 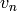 , where
, where 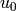 is self,
is self,
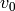 is other,
is other, 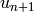 is the arithmetic mean
of
is the arithmetic mean
of 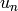 and
and 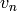 , and
, and 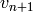 is the
geometric mean of u_n and v_n. If any operand is negative, the
return value is NaN.
is the
geometric mean of u_n and v_n. If any operand is negative, the
return value is NaN.
INPUT:
- right – another real number
OUTPUT:
- the AGM of self and other
EXAMPLES:
sage: a = 1.5
sage: b = 2.5
sage: a.agm(b)
1.96811775182478
sage: RealField(200)(a).agm(b)
1.9681177518247777389894630877503739489139488203685819712291
sage: a.agm(100)
28.1189391225320
The AGM always lies between the geometric and arithmetic mean:
sage: sqrt(a*b) < a.agm(b) < (a+b)/2
True
It is, of course, symmetric:
sage: b.agm(a)
1.96811775182478
and satisfies the relation 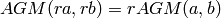 :
:
sage: (2*a).agm(2*b) / 2
1.96811775182478
sage: (3*a).agm(3*b) / 3
1.96811775182478
It is also related to the elliptic integral 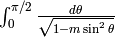 .
.
sage: m = (a-b)^2/(a+b)^2
sage: E = numerical_integral(1/sqrt(1-m*sin(x)^2), 0, RR.pi()/2)[0]
sage: RR.pi()/4 * (a+b)/E
1.96811775182478
TESTS:
sage: 1.5.agm(0)
0.000000000000000
Returns a polynomial of degree at most  which is
approximately satisfied by this number. Note that the returned
polynomial need not be irreducible, and indeed usually won’t be if
this number is a good approximation to an algebraic number of
degree less than
which is
approximately satisfied by this number. Note that the returned
polynomial need not be irreducible, and indeed usually won’t be if
this number is a good approximation to an algebraic number of
degree less than  .
.
ALGORITHM: Uses the PARI C-library algdep command.
EXAMPLE:
sage: r = sqrt(2.0); r
1.41421356237310
sage: r.algdep(5)
x^2 - 2
Returns a polynomial of degree at most  which is
approximately satisfied by this number. Note that the returned
polynomial need not be irreducible, and indeed usually won’t be if
this number is a good approximation to an algebraic number of
degree less than
which is
approximately satisfied by this number. Note that the returned
polynomial need not be irreducible, and indeed usually won’t be if
this number is a good approximation to an algebraic number of
degree less than  .
.
ALGORITHM: Uses the PARI C-library algdep command.
EXAMPLE:
sage: r = sqrt(2.0); r
1.41421356237310
sage: r.algdep(5)
x^2 - 2
Returns the inverse cosine of this number
EXAMPLES:
sage: q = RR.pi()/3
sage: i = q.cos()
sage: i.arccos() == q
True
Returns the hyperbolic inverse cosine of this number
EXAMPLES:
sage: q = RR.pi()/2
sage: i = q.cosh() ; i
2.50917847865806
sage: q == i.arccosh()
True
Returns the inverse hyperbolic cotangent of this number
EXAMPLES:
sage: q = RR.pi()/5
sage: i = q.coth()
sage: i.arccoth() == q
True
Returns the inverse hyperbolic cosecant of this number
EXAMPLES:
sage: i = RR.pi()/5
sage: q = i.csch()
sage: q.arccsch() == i
True
Returns the inverse hyperbolic secant of this number
EXAMPLES:
sage: i = RR.pi()/3
sage: q = i.sech()
sage: q.arcsech() == i
True
Returns the inverse sine of this number
EXAMPLES:
sage: q = RR.pi()/5
sage: i = q.sin()
sage: i.arcsin() == q
True
sage: i.arcsin() - q
0.000000000000000
Returns the hyperbolic inverse sine of this number
EXAMPLES:
sage: q = RR.pi()/7
sage: i = q.sinh() ; i
0.464017630492991
sage: i.arcsinh() - q
0.000000000000000
Returns the inverse tangent of this number
EXAMPLES:
sage: q = RR.pi()/5
sage: i = q.tan()
sage: i.arctan() == q
True
Returns the hyperbolic inverse tangent of this number
EXAMPLES:
sage: q = RR.pi()/7
sage: i = q.tanh() ; i
0.420911241048535
sage: i.arctanh() - q
0.000000000000000
Returns the ceiling of this number
OUTPUT: integer
EXAMPLES:
sage: (2.99).ceil()
3
sage: (2.00).ceil()
2
sage: (2.01).ceil()
3
sage: ceil(10^16 * 1.0)
10000000000000000
sage: ceil(10^17 * 1.0)
100000000000000000
sage: ceil(RR(+infinity))
...
ValueError: Calling ceil() on infinity or NaN
Returns the ceiling of this number
OUTPUT: integer
EXAMPLES:
sage: (2.99).ceil()
3
sage: (2.00).ceil()
2
sage: (2.01).ceil()
3
sage: ceil(10^16 * 1.0)
10000000000000000
sage: ceil(10^17 * 1.0)
100000000000000000
sage: ceil(RR(+infinity))
...
ValueError: Calling ceil() on infinity or NaN
Return the complex conjugate of this real number, which is the number itself.
EXAMPLES:
sage: x = RealField(100)(1.238)
sage: x.conjugate()
1.2380000000000000000000000000
Returns the cosine of this number
EXAMPLES:
sage: t=RR.pi()/2
sage: t.cos()
6.12323399573677e-17
Returns the hyperbolic cosine of this number
EXAMPLES:
sage: q = RR.pi()/12
sage: q.cosh()
1.03446564009551
Returns the cotangent of this number
EXAMPLES:
sage: RealField(100)(2).cot()
-0.45765755436028576375027741043
Returns the hyperbolic cotangent of this number
EXAMPLES:
sage: RealField(100)(2).coth()
1.0373147207275480958778097648
Returns the cosecant of this number
EXAMPLES:
sage: RealField(100)(2).csc()
1.0997501702946164667566973970
Returns the hyperbolic cosecant of this number
EXAMPLES:
sage: RealField(100)(2).csch()
0.27572056477178320775835148216
Return the cubic root (defined over the real numbers) of self.
EXAMPLES:
sage: r = 125.0; r.cube_root()
5.00000000000000
sage: r = -119.0
sage: r.cube_root()^3 - r # illustrates precision loss
-1.42108547152020e-14
Returns the exponential integral of this number.
EXAMPLES:
sage: r = 1.0
sage: r.eint()
1.89511781635594
sage: r = -1.0
sage: r.eint()
NaN
Returns the value of the error function on self.
EXAMPLES:
sage: R = RealField(53)
sage: R(2).erf()
0.995322265018953
sage: R(6).erf()
1.00000000000000
Returns the value of the complementary error function on self,
i.e., 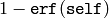 .
.
EXAMPLES:
sage: R = RealField(53)
sage: R(2).erfc()
0.00467773498104727
sage: R(6).erfc()
2.15197367124989e-17
Returns the exact rational representation of this floating-point number.
EXAMPLES:
sage: RR(0).exact_rational()
0
sage: RR(1/3).exact_rational()
6004799503160661/18014398509481984
sage: RR(37/16).exact_rational()
37/16
sage: RR(3^60).exact_rational()
42391158275216203520420085760
sage: RR(3^60).exact_rational() - 3^60
6125652559
sage: RealField(5)(-pi).exact_rational()
-25/8
TESTS:
sage: RR('nan').exact_rational()
...
ValueError: Cannot convert NaN or infinity to rational number
sage: RR('-infinity').exact_rational()
...
ValueError: Cannot convert NaN or infinity to rational number
Returns 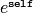
EXAMPLES:
sage: r = 0.0
sage: r.exp()
1.00000000000000
sage: r = 32.3
sage: a = r.exp(); a
1.06588847274864e14
sage: a.log()
32.3000000000000
sage: r = -32.3
sage: r.exp()
9.38184458849869e-15
Returns 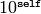
EXAMPLES:
sage: r = 0.0
sage: r.exp10()
1.00000000000000
sage: r = 32.0
sage: r.exp10()
1.00000000000000e32
sage: r = -32.3
sage: r.exp10()
5.01187233627276e-33
Returns 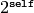
EXAMPLES:
sage: r = 0.0
sage: r.exp2()
1.00000000000000
sage: r = 32.0
sage: r.exp2()
4.29496729600000e9
sage: r = -32.3
sage: r.exp2()
1.89117248253021e-10
Returns 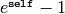 , avoiding cancellation
near 0.
, avoiding cancellation
near 0.
EXAMPLES:
sage: r = 1.0
sage: r.expm1()
1.71828182845905
sage: r = 1e-16
sage: exp(r)-1
0.000000000000000
sage: r.expm1()
1.00000000000000e-16
Returns the floor of this number
EXAMPLES:
sage: R = RealField()
sage: (2.99).floor()
2
sage: (2.00).floor()
2
sage: floor(RR(-5/2))
-3
sage: floor(RR(+infinity))
...
ValueError: Calling floor() on infinity or NaN
Returns the floating-point rank of this number. That is, if you
list the floating-point numbers of this precision in order, and
number them starting with 0.0  0 and extending
the list to positive and negative infinity, returns the number
corresponding to this floating-point number.
0 and extending
the list to positive and negative infinity, returns the number
corresponding to this floating-point number.
EXAMPLES:
sage: RR(0).fp_rank()
0
sage: RR(0).nextabove().fp_rank()
1
sage: RR(0).nextbelow().nextbelow().fp_rank()
-2
sage: RR(1).fp_rank()
4835703278458516698824705
sage: RR(-1).fp_rank()
-4835703278458516698824705
sage: RR(1).fp_rank() - RR(1).nextbelow().fp_rank()
1
sage: RR(-infinity).fp_rank()
-9671406552413433770278913
sage: RR(-infinity).fp_rank() - RR(-infinity).nextabove().fp_rank()
-1
Return the floating-point rank delta between self and other. That is, if the return value is positive, this is the number of times you have to call .nextabove() to get from self to other.
EXAMPLES:
sage: [x.fp_rank_delta(x.nextabove()) for x in
... (RR(-infinity), -1.0, 0.0, 1.0, RR(pi), RR(infinity))]
[1, 1, 1, 1, 1, 0]
In the 2-bit floating-point field, one subsegment of the floating-point numbers is: 1, 1.5, 2, 3, 4, 6, 8, 12, 16, 24, 32
sage: R2 = RealField(2)
sage: R2(1).fp_rank_delta(R2(2))
2
sage: R2(2).fp_rank_delta(R2(1))
-2
sage: R2(1).fp_rank_delta(R2(1048576))
40
sage: R2(24).fp_rank_delta(R2(4))
-5
sage: R2(-4).fp_rank_delta(R2(-24))
-5
There are lots of floating-point numbers around 0:
sage: R2(-1).fp_rank_delta(R2(1))
4294967298
Returns a real number such that self = self.trunc() + self.frac()`. The return value will also satisfy ``-1 < self.frac() < 1.
EXAMPLES:
sage: (2.99).frac()
0.990000000000000
sage: (2.50).frac()
0.500000000000000
sage: (-2.79).frac()
-0.790000000000000
sage: (-2.79).trunc() + (-2.79).frac()
-2.79000000000000
The Euler gamma function. Return gamma of self.
EXAMPLES:
sage: R = RealField()
sage: R(6).gamma()
120.000000000000
sage: R(1.5).gamma()
0.886226925452758
Return the imaginary part of self.
(Since self is a real number, this simply returns exactly 0.)
EXAMPLES:
sage: RR.pi().imag()
0
sage: RealField(100)(2).imag()
0
If in decimal this number is written n.defg, returns n.
OUTPUT: a Sage Integer
EXAMPLE:
sage: a = 119.41212
sage: a.integer_part()
119
sage: a = -123.4567
sage: a.integer_part()
-123
A big number with no decimal point:
sage: a = RR(10^17); a
1.00000000000000e17
sage: a.integer_part()
100000000000000000
Return True if self is infinite and False otherwise.
EXAMPLES:
sage: a = RR('1.494') / RR(0); a
+infinity
sage: a.is_infinity()
True
sage: a = -RR('1.494') / RR(0); a
-infinity
sage: a.is_infinity()
True
sage: RR(1.5).is_infinity()
False
sage: RR('nan').is_infinity()
False
EXAMPLES:
sage: a = RR('1.494') / RR(0); a
+infinity
sage: a.is_negative_infinity()
False
sage: a = -RR('1.494') / RR(0); a
-infinity
sage: RR(1.5).is_negative_infinity()
False
sage: a.is_negative_infinity()
True
EXAMPLES:
sage: a = RR('1.494') / RR(0); a
+infinity
sage: a.is_positive_infinity()
True
sage: a = -RR('1.494') / RR(0); a
-infinity
sage: RR(1.5).is_positive_infinity()
False
sage: a.is_positive_infinity()
False
Return True if self is real (of course, this always returns True for a finite element of a real field).
EXAMPLES:
sage: RR(1).is_real()
True
sage: RR('-100').is_real()
True
Returns whether or not this number is a square in this field. For the real numbers, this is True if and only if self is non-negative.
EXAMPLES:
sage: r = 3.5
sage: r.is_square()
True
sage: r = 0.0
sage: r.is_square()
True
sage: r = -4.0
sage: r.is_square()
False
Return True if self is a unit (has a multiplicative inverse) and False otherwise.
EXAMPLES:
sage: RR(1).is_unit()
True
sage: RR('0').is_unit()
False
sage: RR('-0').is_unit()
False
sage: RR('nan').is_unit()
False
sage: RR('inf').is_unit()
False
sage: RR('-inf').is_unit()
False
Returns the value of the Bessel J function of order 0 at self.
EXAMPLES:
sage: R = RealField(53)
sage: R(2).j0()
0.223890779141236
Returns the value of the Bessel J function of order 1 at self.
EXAMPLES:
sage: R = RealField(53)
sage: R(2).j1()
0.576724807756873
Returns the value of the Bessel J function of order  at
self.
at
self.
EXAMPLES:
sage: R = RealField(53)
sage: R(2).jn(3)
0.128943249474402
sage: R(2).jn(-17)
-2.65930780516787e-15
This method is deprecated, please use log_gamma() instead.
See the log_gamma() method for documentation and examples.
EXAMPLES:
sage: RR(6).lngamma()
doctest:...: DeprecationWarning: The method lngamma() is deprecated. Use log_gamma() instead.
4.78749174278205
EXAMPLES:
sage: R = RealField()
sage: R(2).log()
0.693147180559945
sage: log(RR(2))
0.693147180559945
sage: log(RR(2),e)
0.693147180559945
sage: r = R(-1); r.log()
3.14159265358979*I
sage: log(RR(-1),e)
3.14159265358979*I
sage: r.log(2)
4.53236014182719*I
Returns log to the base 10 of self
EXAMPLES:
sage: r = 16.0; r.log10()
1.20411998265592
sage: r.log() / log(10.0)
1.20411998265592
sage: r = 39.9; r.log10()
1.60097289568675
sage: r = 0.0
sage: r.log10()
-infinity
sage: r = -1.0
sage: r.log10()
1.36437635384184*I
Returns log base e of 1 + self
EXAMPLES:
sage: r = 15.0; r.log1p()
2.77258872223978
sage: (r+1).log()
2.77258872223978
sage: r = 38.9; r.log1p()
3.68637632389582
sage: r = -1.0
sage: r.log1p()
-infinity
sage: r = -2.0
sage: r.log1p()
3.14159265358979*I
Returns log to the base 2 of self
EXAMPLES:
sage: r = 16.0
sage: r.log2()
4.00000000000000
sage: r = 31.9; r.log2()
4.99548451887751
sage: r = 0.0
sage: r.log2()
-infinity
sage: r = -3.0; r.log2()
1.58496250072116 + 4.53236014182719*I
Return the logarithm of gamma of self.
EXAMPLES:
sage: R = RealField(53)
sage: R(6).log_gamma()
4.78749174278205
sage: R(1e10).log_gamma()
2.20258509288811e11
Return the multiplicative order of self.
EXAMPLES:
sage: RR(1).multiplicative_order()
1
sage: RR(-1).multiplicative_order()
2
sage: RR(3).multiplicative_order()
+Infinity
Find a rational near to self. Exactly one of max_error or max_denominator must be specified. If max_error is specified, then this returns the simplest rational in the range [self-max_error .. self+max_error]. If max_denominator is specified, then this returns the rational closest to self with denominator at most max_denominator. (In case of ties, we pick the simpler rational.)
EXAMPLES:
sage: (0.333).nearby_rational(max_error=0.001)
1/3
sage: (0.333).nearby_rational(max_error=1)
0
sage: (-0.333).nearby_rational(max_error=0.0001)
-257/772
sage: (0.333).nearby_rational(max_denominator=100)
1/3
sage: RR(1/3 + 1/1000000).nearby_rational(max_denominator=2999999)
777780/2333333
sage: RR(1/3 + 1/1000000).nearby_rational(max_denominator=3000000)
1000003/3000000
sage: (-0.333).nearby_rational(max_denominator=1000)
-333/1000
sage: RR(3/4).nearby_rational(max_denominator=2)
1
sage: RR(pi).nearby_rational(max_denominator=120)
355/113
sage: RR(pi).nearby_rational(max_denominator=10000)
355/113
sage: RR(pi).nearby_rational(max_denominator=100000)
312689/99532
sage: RR(pi).nearby_rational(max_denominator=1)
3
sage: RR(-3.5).nearby_rational(max_denominator=1)
-3
TESTS:
sage: RR('nan').nearby_rational(max_denominator=1000)
...
ValueError: Cannot convert NaN or infinity to rational number
sage: RR('nan').nearby_rational(max_error=0.01)
...
ValueError: Cannot convert NaN or infinity to rational number
sage: RR('infinity').nearby_rational(max_denominator=1000)
...
ValueError: Cannot convert NaN or infinity to rational number
sage: RR('infinity').nearby_rational(max_error=0.01)
...
ValueError: Cannot convert NaN or infinity to rational number
Returns the next floating-point number larger than self.
EXAMPLES:
sage: RR('-infinity').nextabove()
-2.09857871646739e323228496
sage: RR(0).nextabove()
2.38256490488795e-323228497
sage: RR('+infinity').nextabove()
+infinity
sage: RR(-sqrt(2)).str(truncate=False)
'-1.4142135623730951'
sage: RR(-sqrt(2)).nextabove().str(truncate=False)
'-1.4142135623730949'
Returns the next floating-point number smaller than self.
EXAMPLES:
sage: RR('-infinity').nextbelow()
-infinity
sage: RR(0).nextbelow()
-2.38256490488795e-323228497
sage: RR('+infinity').nextbelow()
2.09857871646739e323228496
sage: RR(-sqrt(2)).str(truncate=False)
'-1.4142135623730951'
sage: RR(-sqrt(2)).nextbelow().str(truncate=False)
'-1.4142135623730954'
Returns the floating-point number adjacent to self which is closer to other. If self or other is NaN, returns NaN; if self equals other, returns self.
EXAMPLES:
sage: (1.0).nexttoward(2).str(truncate=False)
'1.0000000000000002'
sage: (1.0).nexttoward(RR('-infinity')).str(truncate=False)
'0.99999999999999989'
sage: RR(infinity).nexttoward(0)
2.09857871646739e323228496
sage: RR(pi).str(truncate=False)
'3.1415926535897931'
sage: RR(pi).nexttoward(22/7).str(truncate=False)
'3.1415926535897936'
sage: RR(pi).nexttoward(21/7).str(truncate=False)
'3.1415926535897927'
Returns an 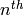 root of self.
root of self.
INPUT:
 should be less than
`sys.maxint`.
should be less than
`sys.maxint`.AUTHORS:
EXAMPLES:
sage: R = RealField()
sage: R(8).nth_root(3)
2.00000000000000
sage: R(8).nth_root(3.7) # illustrate rounding down
2.00000000000000
sage: R(-8).nth_root(3)
-2.00000000000000
sage: R(0).nth_root(3)
0.000000000000000
sage: R(32).nth_root(-1)
...
ValueError: n must be positive
sage: R(32).nth_root(1.0)
32.0000000000000
sage: R(4).nth_root(4)
1.41421356237310
sage: R(4).nth_root(40)
1.03526492384138
sage: R(4).nth_root(400)
1.00347174850950
sage: R(4).nth_root(4000)
1.00034663365385
sage: R(4).nth_root(4000000)
1.00000034657365
sage: R(-27).nth_root(3)
-3.00000000000000
sage: R(-4).nth_root(3999999)
-1.00000034657374
Note that for negative numbers, any even root throws an exception
sage: R(-2).nth_root(6)
...
ValueError: taking an even root of a negative number
The 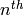 root of 0 is defined to be 0, for any
root of 0 is defined to be 0, for any

sage: R(0).nth_root(6)
0.000000000000000
sage: R(0).nth_root(7)
0.000000000000000
TESTS: The old and new algorithms should give exactly the same results in all cases.
sage: def check(x, n):
... answers = []
... for sign in (1, -1):
... if is_even(n) and sign == -1:
... continue
... for rounding in ('RNDN', 'RNDD', 'RNDU', 'RNDZ'):
... fld = RealField(x.prec(), rnd=rounding)
... fx = fld(sign * x)
... alg_mpfr = fx.nth_root(n, algorithm=1)
... alg_mpfi = fx.nth_root(n, algorithm=2)
... assert(alg_mpfr == alg_mpfi)
... if sign == 1: answers.append(alg_mpfr)
... return answers
Check some perfect powers (and nearby numbers).
sage: check(16.0, 4)
[2.00000000000000, 2.00000000000000, 2.00000000000000, 2.00000000000000]
sage: check((16.0).nextabove(), 4)
[2.00000000000000, 2.00000000000000, 2.00000000000001, 2.00000000000000]
sage: check((16.0).nextbelow(), 4)
[2.00000000000000, 1.99999999999999, 2.00000000000000, 1.99999999999999]
sage: check(((9.0 * 256)^7), 7)
[2304.00000000000, 2304.00000000000, 2304.00000000000, 2304.00000000000]
sage: check(((9.0 * 256)^7).nextabove(), 7)
[2304.00000000000, 2304.00000000000, 2304.00000000001, 2304.00000000000]
sage: check(((9.0 * 256)^7).nextbelow(), 7)
[2304.00000000000, 2303.99999999999, 2304.00000000000, 2303.99999999999]
sage: check(((5.0 / 512)^17), 17)
[0.00976562500000000, 0.00976562500000000, 0.00976562500000000, 0.00976562500000000]
sage: check(((5.0 / 512)^17).nextabove(), 17)
[0.00976562500000000, 0.00976562500000000, 0.00976562500000001, 0.00976562500000000]
sage: check(((5.0 / 512)^17).nextbelow(), 17)
[0.00976562500000000, 0.00976562499999999, 0.00976562500000000, 0.00976562499999999]
And check some non-perfect powers:
sage: check(2.0, 3)
[1.25992104989487, 1.25992104989487, 1.25992104989488, 1.25992104989487]
sage: check(2.0, 4)
[1.18920711500272, 1.18920711500272, 1.18920711500273, 1.18920711500272]
sage: check(2.0, 5)
[1.14869835499704, 1.14869835499703, 1.14869835499704, 1.14869835499703]
And some different precisions:
sage: check(RealField(20)(22/7), 19)
[1.0621, 1.0621, 1.0622, 1.0621]
sage: check(RealField(200)(e), 4)
[1.2840254166877414840734205680624364583362808652814630892175, 1.2840254166877414840734205680624364583362808652814630892175, 1.2840254166877414840734205680624364583362808652814630892176, 1.2840254166877414840734205680624364583362808652814630892175]
EXAMPLES:
sage: R = RealField()
sage: a = R('1.2456')
sage: a.parent()
Real Field with 53 bits of precision
Return the precision of self.
EXAMPLES:
sage: RR(1.0).precision()
53
sage: RealField(101)(-1).precision()
101
Return the precision of self.
EXAMPLES:
sage: RR(1.0).precision()
53
sage: RealField(101)(-1).precision()
101
Return the real part of self.
(Since self is a real number, this simply returns self.)
EXAMPLES:
sage: RR(2).real()
2.00000000000000
sage: RealField(200)(-4.5).real()
-4.5000000000000000000000000000000000000000000000000000000000
Rounds self to the nearest integer. The rounding mode of the parent field has no effect on this function.
EXAMPLES:
sage: RR(0.49).round()
0
sage: RR(0.5).round()
1
sage: RR(-0.49).round()
0
sage: RR(-0.5).round()
-1
Returns the secant of this number
EXAMPLES:
sage: RealField(100)(2).sec()
-2.4029979617223809897546004014
Returns the hyperbolic secant of this number
EXAMPLES:
sage: RealField(100)(2).sech()
0.26580222883407969212086273982
Return +1 if self is positive, -1 if self is negative, and 0 if self is zero.
EXAMPLES:
sage: R=RealField(100)
sage: R(-2.4).sign()
-1
sage: R(2.1).sign()
1
sage: R(0).sign()
0
Return the sign, mantissa, and exponent of self.
In Sage (as in MPFR), floating-point numbers of precision  are of the form
are of the form 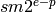 , where
, where 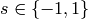 ,
,
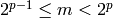 , and
, and 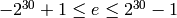 ; plus the special values +0, -0, +infinity,
-infinity, and NaN (which stands for Not-a-Number).
; plus the special values +0, -0, +infinity,
-infinity, and NaN (which stands for Not-a-Number).
This function returns s, m, and e-p. For the special values:
- ``+0`` returns (1, 0, 0) (analogous to IEEE-754; note that MPFR actually stores the exponent as ``smallest exponent possible``)
- ``-0`` returns (-1, 0, 0) (analogous to IEEE-754; note that MPFR actually stores the exponent as ``smallest exponent possible``)
- the return values for ``+infinity``, ``-infinity``, and
``NaN`` are not specified.
EXAMPLES::
sage: R=RealField(53)
sage: a=R(exp(1.0)); a
2.71828182845905
sage: sign,mantissa,exponent=R(exp(1.0)).sign_mantissa_exponent()
sage: sign,mantissa,exponent
(1, 6121026514868073, -51)
sage: sign*mantissa*(2**exponent)==a
True
We can also calculate this also using p-adic valuations::
sage: a=R(exp(1.0))
sage: b=a.exact_rational()
sage: valuation, unit = b.val_unit(2)
sage: (b/abs(b), unit, valuation)
(1, 6121026514868073, -51)
sage: a.sign_mantissa_exponent()
(1, 6121026514868073, -51)
TESTS::
sage: R('+0').sign_mantissa_exponent()
(1, 0, 0)
sage: R('-0').sign_mantissa_exponent()
(-1, 0, 0)
Returns the simplest rational which is equal to self (in the Sage sense). Recall that Sage defines the equality operator by coercing both sides to a single type and then comparing; thus, this finds the simplest rational which (when coerced to this RealField) is equal to self.
Given rationals a/b and c/d (both in lowest terms), the former is
simpler if b<d or if b==d and 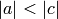 .
.
The effect of rounding modes is slightly counter-intuitive. Consider the case of round-toward-minus-infinity. This rounding is performed when coercing a rational to a floating-point number; so the simplest_rational() of a round-to-minus-infinity number will be either exactly equal to or slightly larger than the number.
EXAMPLES:
sage: RRd = RealField(53, rnd='RNDD')
sage: RRz = RealField(53, rnd='RNDZ')
sage: RRu = RealField(53, rnd='RNDU')
sage: def check(x):
... rx = x.simplest_rational()
... assert(x == rx)
... return rx
sage: RRd(1/3) < RRu(1/3)
True
sage: check(RRd(1/3))
1/3
sage: check(RRu(1/3))
1/3
sage: check(RRz(1/3))
1/3
sage: check(RR(1/3))
1/3
sage: check(RRd(-1/3))
-1/3
sage: check(RRu(-1/3))
-1/3
sage: check(RRz(-1/3))
-1/3
sage: check(RR(-1/3))
-1/3
sage: check(RealField(20)(pi))
355/113
sage: check(RR(pi))
245850922/78256779
sage: check(RR(2).sqrt())
131836323/93222358
sage: check(RR(1/2^210))
1/1645504557321205859467264516194506011931735427766374553794641921
sage: check(RR(2^210))
1645504557321205950811116849375918117252433820865891134852825088
sage: (RR(17).sqrt()).simplest_rational()^2 - 17
-1/348729667233025
sage: (RR(23).cube_root()).simplest_rational()^3 - 23
-1404915133/264743395842039084891584
sage: RRd5 = RealField(5, rnd='RNDD')
sage: RRu5 = RealField(5, rnd='RNDU')
sage: RR5 = RealField(5)
sage: below1 = RR5(1).nextbelow()
sage: check(RRd5(below1))
31/32
sage: check(RRu5(below1))
16/17
sage: check(below1)
21/22
sage: below1.exact_rational()
31/32
sage: above1 = RR5(1).nextabove()
sage: check(RRd5(above1))
10/9
sage: check(RRu5(above1))
17/16
sage: check(above1)
12/11
sage: above1.exact_rational()
17/16
sage: check(RR(1234))
1234
sage: check(RR5(1234))
1185
sage: check(RR5(1184))
1120
sage: RRd2 = RealField(2, rnd='RNDD')
sage: RRu2 = RealField(2, rnd='RNDU')
sage: RR2 = RealField(2)
sage: check(RR2(8))
7
sage: check(RRd2(8))
8
sage: check(RRu2(8))
7
sage: check(RR2(13))
11
sage: check(RRd2(13))
12
sage: check(RRu2(13))
13
sage: check(RR2(16))
14
sage: check(RRd2(16))
16
sage: check(RRu2(16))
13
sage: check(RR2(24))
21
sage: check(RRu2(24))
17
sage: check(RR2(-24))
-21
sage: check(RRu2(-24))
-24
TESTS:
sage: RR('nan').simplest_rational()
...
ValueError: Cannot convert NaN or infinity to rational number
sage: RR('-infinity').simplest_rational()
...
ValueError: Cannot convert NaN or infinity to rational number
Returns the sine of this number
EXAMPLES:
sage: R = RealField(100)
sage: R(2).sin()
0.90929742682568169539601986591
Returns a pair consisting of the sine and cosine.
EXAMPLES:
sage: R = RealField()
sage: t = R.pi()/6
sage: t.sincos()
(0.500000000000000, 0.866025403784439)
Returns the hyperbolic sine of this number
EXAMPLES:
sage: q = RR.pi()/12
sage: q.sinh()
0.264800227602271
The square root function.
INPUT:
EXAMPLES:
sage: r = -2.0
sage: r.sqrt()
1.41421356237310*I
sage: r = 4.0
sage: r.sqrt()
2.00000000000000
sage: r.sqrt()^2 == r
True
sage: r = 4344
sage: r.sqrt()
2*sqrt(1086)
sage: r = 4344.0
sage: r.sqrt()^2 == r
True
sage: r.sqrt()^2 - r
0.000000000000000
sage: r = -2.0
sage: r.sqrt()
1.41421356237310*I
INPUT:
EXAMPLES:
sage: a = 61/3.0; a
20.3333333333333
sage: a.str(truncate=False)
'20.333333333333332'
sage: a.str(2)
'10100.010101010101010101010101010101010101010101010101'
sage: a.str(no_sci=False)
'2.03333333333333e1'
sage: a.str(16, no_sci=False)
'1.4555555555555@1'
sage: b = 2.0^99
sage: b.str()
'6.33825300114115e29'
sage: b.str(no_sci=False)
'6.33825300114115e29'
sage: b.str(no_sci=True)
'6.33825300114115e29'
sage: c = 2.0^100
sage: c.str()
'1.26765060022823e30'
sage: c.str(no_sci=False)
'1.26765060022823e30'
sage: c.str(no_sci=True)
'1.26765060022823e30'
sage: c.str(no_sci=2)
'1267650600228230000000000000000.'
sage: 0.5^53
1.11022302462516e-16
sage: 0.5^54
5.55111512312578e-17
sage: (0.01).str()
'0.0100000000000000'
sage: (0.01).str(skip_zeroes=True)
'0.01'
sage: (-10.042).str()
'-10.0420000000000'
sage: (-10.042).str(skip_zeroes=True)
'-10.042'
sage: (389.0).str(skip_zeroes=True)
'389.'
Returns the tangent of this number
EXAMPLES:
sage: q = RR.pi()/3
sage: q.tan()
1.73205080756888
sage: q = RR.pi()/6
sage: q.tan()
0.577350269189626
Returns the hyperbolic tangent of this number
EXAMPLES:
sage: q = RR.pi()/11
sage: q.tanh()
0.278079429295850
Truncates this number
EXAMPLES:
sage: (2.99).trunc()
2
sage: (-0.00).trunc()
0
sage: (0.00).trunc()
0
Returns the unit of least precision of self, which is the weight of the least significant bit of self. Unless self is exactly a power of two, it is gap between this number and the next closest distinct number that can be represented.
EXAMPLES:
sage: a = 1.0
sage: a + a.ulp() == a
False
sage: a + a.ulp()/2 == a
True
sage: a = RealField(500).pi()
sage: b = a + a.ulp()
sage: (a+b)/2 in [a,b]
True
sage: a = RR(infinity)
sage: a.ulp()
+infinity
sage: (-a).ulp()
+infinity
sage: a = RR('nan')
sage: a.ulp() is a
True
Returns the value of the Bessel Y function of order 0 at self.
EXAMPLES:
sage: R = RealField(53)
sage: R(2).y0()
0.510375672649745
Returns the value of the Bessel Y function of order 1 at self.
EXAMPLES:
sage: R = RealField(53)
sage: R(2).y1()
-0.107032431540938
Returns the value of the Bessel Y function of order  at
self.
at
self.
EXAMPLES:
sage: R = RealField(53)
sage: R(2).yn(3)
-1.12778377684043
sage: R(2).yn(-17)
7.09038821729481e12
Return the Riemann zeta function evaluated at this real number.
EXAMPLES:
sage: R = RealField()
sage: R(2).zeta()
1.64493406684823
sage: R.pi()^2/6
1.64493406684823
sage: R(-2).zeta()
0.000000000000000
sage: R(1).zeta()
+infinity
Computing zeta using PARI is much more efficient in difficult cases. Here’s how to compute zeta with at least a given precision:
sage: z = pari(2).zeta(precision=53); z
1.64493406684823
sage: pari(2).zeta(precision=128).python().prec()
128
sage: pari(2).zeta(precision=65).python().prec()
128 # 64-bit
96 # 32-bit
Note that the number of bits of precision in the constructor only effects the internal precision of the pari number, which is rounded up to the nearest multiple of 32 or 64. To increase the number of digits that gets displayed you must use pari.set_real_precision.
sage: type(z)
<type 'sage.libs.pari.gen.gen'>
sage: R(z)
1.64493406684823
Return the real number defined by the string s as an element of RealField(prec=n), where n potentially has slightly more (controlled by pad) bits than given by s.
INPUT:
EXAMPLES:
sage: RealNumber('2.3')
2.30000000000000
sage: RealNumber(10)
10.0000000000000
sage: RealNumber('1.0000000000000000000000000000000000')
1.000000000000000000000000000000000
sage: RealField(200)(1.2)
1.2000000000000000000000000000000000000000000000000000000000
sage: (1.2).parent() is RR
True
TESTS:
sage: RealNumber('.000000000000000000000000000000001').prec()
53
sage: RealNumber('-.000000000000000000000000000000001').prec()
53
Returns True if x is technically of a Python real field type.
EXAMPLES:
sage: sage.rings.real_mpfr.is_RealField(RR)
True
sage: sage.rings.real_mpfr.is_RealField(CC)
False
Return True if x is of type RealNumber, meaning that it is an element of the MPFR real field with some precision.
EXAMPLES:
sage: from sage.rings.real_mpfr import is_RealNumber
sage: is_RealNumber(2.5)
True
sage: is_RealNumber(float(2.3))
False
sage: is_RealNumber(RDF(2))
False
sage: is_RealNumber(pi)
False
TESTS:
sage: R = RealField(2147483647)
sage: R
Real Field with 2147483647 bits of precision
sage: R = RealField(2147483648)
...
OverflowError: ... too large to convert to int