EXAMPLES:
We create the real double vector space of dimension 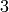 :
:
sage: V = RDF^3; V
Vector space of dimension 3 over Real Double Field
Notice that this space is unique.
sage: V is RDF^3
True
sage: V is FreeModule(RDF, 3)
True
sage: V is VectorSpace(RDF, 3)
True
Also, you can instantly create a space of large dimension.
sage: V = RDF^10000
TESTS:
Test NumPy conversions::
sage: RDF(1).__array_interface__
{'typestr': '=f8'}
sage: import numpy
sage: numpy.array([RDF.pi()]).dtype
dtype('float64')
Bases: sage.structure.element.FieldElement
An approximation to a real number using double precision floating point numbers. Answers derived from calculations with such approximations may differ from what they would be if those calculations were performed with true real numbers. This is due to the rounding errors inherent to finite precision calculations.
EXAMPLES:
sage: RDF.NaN()
NaN
Returns the absolute value of self.
EXAMPLES:
sage: RDF(1e10).abs()
10000000000.0
sage: RDF(-1e10).abs()
10000000000.0
Returns the hyperbolic inverse cosine of this number
EXAMPLES:
sage: q = RDF.pi()/2
sage: i = q.cosh() ; i
2.50917847866
sage: abs(i.acosh()-q) < 1e-15
True
Return the arithmetic-geometric mean of self and other. The
arithmetic-geometric mean is the common limit of the sequences
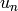 and
and 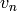 , where
, where 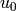 is self,
is self,
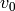 is other,
is other, 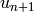 is the arithmetic mean
of
is the arithmetic mean
of 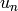 and
and 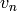 , and
, and 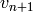 is the
geometric mean of u_n and v_n. If any operand is negative, the
return value is NaN.
is the
geometric mean of u_n and v_n. If any operand is negative, the
return value is NaN.
EXAMPLES:
sage: a = RDF(1.5)
sage: b = RDF(2.3)
sage: a.agm(b)
1.87864845581
The arithmetic-geometric mean always lies between the geometric and arithmetic mean.
sage: sqrt(a*b) < a.agm(b) < (a+b)/2
True
Returns a polynomial of degree at most  which is
approximately satisfied by this number. Note that the returned
polynomial need not be irreducible, and indeed usually won’t be if
this number is a good approximation to an algebraic number of
degree less than
which is
approximately satisfied by this number. Note that the returned
polynomial need not be irreducible, and indeed usually won’t be if
this number is a good approximation to an algebraic number of
degree less than  .
.
ALGORITHM: Uses the PARI C-library algdep command.
EXAMPLE:
sage: r = RDF(2).sqrt(); r
1.41421356237
sage: r.algdep(5)
x^2 - 2
Returns a polynomial of degree at most  which is
approximately satisfied by this number. Note that the returned
polynomial need not be irreducible, and indeed usually won’t be if
this number is a good approximation to an algebraic number of
degree less than
which is
approximately satisfied by this number. Note that the returned
polynomial need not be irreducible, and indeed usually won’t be if
this number is a good approximation to an algebraic number of
degree less than  .
.
ALGORITHM: Uses the PARI C-library algdep command.
EXAMPLE:
sage: r = sqrt(RDF(2)); r
1.41421356237
sage: r.algdep(5)
x^2 - 2
Returns the inverse cosine of this number
EXAMPLES:
sage: q = RDF.pi()/3
sage: i = q.cos()
sage: i.arccos() == q
True
Returns the inverse sine of this number
EXAMPLES:
sage: q = RDF.pi()/5
sage: i = q.sin()
sage: i.arcsin() == q
True
Returns the hyperbolic inverse sine of this number
EXAMPLES:
sage: q = RDF.pi()/2
sage: i = q.sinh() ; i
2.30129890231
sage: abs(i.arcsinh()-q) < 1e-15
True
Returns the inverse tangent of this number
EXAMPLES:
sage: q = RDF.pi()/5
sage: i = q.tan()
sage: i.arctan() == q
True
Returns the hyperbolic inverse tangent of this number
EXAMPLES:
sage: q = RDF.pi()/2
sage: i = q.tanh() ; i
0.917152335667
sage: i.arctanh() - q # output is random, depending on arch.
-4.4408920985e-16
Returns the ceiling of this number
OUTPUT: integer
EXAMPLES:
sage: RDF(2.99).ceil()
3
sage: RDF(2.00).ceil()
2
sage: RDF(-5/2).ceil()
-2
Returns the ceiling of this number
OUTPUT: integer
EXAMPLES:
sage: RDF(2.99).ceil()
3
sage: RDF(2.00).ceil()
2
sage: RDF(-5/2).ceil()
-2
Returns the complex conjugate of this real number, which is the real number itself.
EXAMPLES:
sage: RDF(4).conjugate()
4.0
Returns the cosine of this number
EXAMPLES:
sage: t=RDF.pi()/2
sage: t.cos()
6.12323399574e-17
Returns the hyperbolic cosine of this number
EXAMPLES:
sage: q = RDF.pi()/12
sage: q.cosh()
1.0344656401
This function returns the hyperbolic cotangent.
EXAMPLES:
sage: RDF(pi).coth()
1.0037418732
sage: CDF(pi).coth()
1.0037418732
This function returns the hyperbolic cosecant.
EXAMPLES:
sage: RDF(pi).csch()
0.08658953753
sage: CDF(pi).csch()
0.08658953753
Return the cubic root (defined over the real numbers) of self.
EXAMPLES:
sage: r = RDF(125.0); r.cube_root()
5.0
sage: r = RDF(-119.0)
sage: r.cube_root()^3 - r # output is random, depending on arch.
0.0
Returns the value of the error function on self.
EXAMPLES:
sage: RDF(6).erf()
1.0
Returns 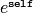
EXAMPLES:
sage: r = RDF(0.0)
sage: r.exp()
1.0
sage: r = RDF('32.3')
sage: a = r.exp(); a
1.06588847275e+14
sage: a.log()
32.3
sage: r = RDF('-32.3')
sage: r.exp()
9.3818445885e-15
sage: RDF(1000).exp()
+infinity
Returns 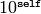
EXAMPLES:
sage: r = RDF(0.0)
sage: r.exp10()
1.0
sage: r = RDF(32.0)
sage: r.exp10()
1e+32
sage: r = RDF(-32.3)
sage: r.exp10()
5.01187233627e-33
Returns 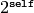
EXAMPLES:
sage: r = RDF(0.0)
sage: r.exp2()
1.0
sage: r = RDF(32.0)
sage: r.exp2()
4294967296.0
sage: r = RDF(-32.3)
sage: r.exp2()
1.89117248253e-10
Returns the floor of this number
EXAMPLES:
sage: RDF(2.99).floor()
2
sage: RDF(2.00).floor()
2
sage: RDF(-5/2).floor()
-3
frac returns a real number > -1 and < 1. it satisfies the relation: x = x.trunc() + x.frac()
EXAMPLES:
sage: RDF(2.99).frac()
0.99
sage: RDF(2.50).frac()
0.5
sage: RDF(-2.79).frac()
-0.79
The Euler gamma function. Return gamma of self.
EXAMPLES:
sage: RDF(6).gamma()
120.0
sage: RDF(1.5).gamma()
0.886226925453
Computes the value 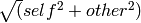 in such a way
as to avoid overflow.
in such a way
as to avoid overflow.
EXAMPLES:
sage: x = RDF(4e300); y = RDF(3e300);
sage: x.hypot(y)
5e+300
sage: sqrt(x^2+y^2) # overflow
+infinity
Returns the imaginary part of this number. (hint: it’s zero.)
EXAMPLES:
sage: a = RDF(3)
sage: a.imag()
0.0
If in decimal this number is written n.defg, returns n.
EXAMPLES:
sage: r = RDF('-1.6')
sage: a = r.integer_part(); a
-1
sage: type(a)
<type 'sage.rings.integer.Integer'>
sage: r = RDF(0.0/0.0)
sage: a = r.integer_part()
...
TypeError: Attempt to get integer part of NaN
EXAMPLES:
sage: RDF(1).is_NaN()
False
sage: a = RDF(0)/RDF(0)
sage: a.is_NaN()
True
EXAMPLES:
sage: a = RDF(2); b = RDF(0)
sage: (a/b).is_infinity()
True
sage: (b/a).is_infinity()
False
EXAMPLES:
sage: a = RDF(2)/RDF(0)
sage: a.is_negative_infinity()
False
sage: a = RDF(-3)/RDF(0)
sage: a.is_negative_infinity()
True
EXAMPLES:
sage: a = RDF(1)/RDF(0)
sage: a.is_positive_infinity()
True
sage: a = RDF(-1)/RDF(0)
sage: a.is_positive_infinity()
False
Returns whether or not this number is a square in this field. For the real numbers, this is True if and only if self is non-negative.
EXAMPLES:
sage: RDF(3.5).is_square()
True
sage: RDF(0).is_square()
True
sage: RDF(-4).is_square()
False
EXAMPLES:
sage: RDF(2).log()
0.69314718056
sage: RDF(2).log(2)
1.0
sage: RDF(2).log(pi)
0.605511561398
sage: RDF(2).log(10)
0.301029995664
sage: RDF(2).log(1.5)
1.70951129135
sage: RDF(0).log()
-infinity
sage: RDF(-1).log()
3.14159265359*I
sage: RDF(-1).log(2)
4.53236014183*I
Returns log to the base 10 of self
EXAMPLES:
sage: r = RDF('16.0'); r.log10()
1.20411998266
sage: r.log() / RDF(log(10))
1.20411998266
sage: r = RDF('39.9'); r.log10()
1.60097289569
Returns log to the base 2 of self
EXAMPLES:
sage: r = RDF(16.0)
sage: r.log2()
4.0
sage: r = RDF(31.9); r.log2()
4.99548451888
Returns log to the base pi of self
EXAMPLES:
sage: r = RDF(16); r.logpi()
2.42204624559
sage: r.log() / RDF(log(pi))
2.42204624559
sage: r = RDF('39.9'); r.logpi()
3.22030233461
Returns  such that self^n == 1.
such that self^n == 1.
Only 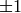 have finite multiplicative order.
have finite multiplicative order.
EXAMPLES:
sage: RDF(1).multiplicative_order()
1
sage: RDF(-1).multiplicative_order()
2
sage: RDF(3).multiplicative_order()
+Infinity
EXAMPLES:
sage: RDF.nan()
NaN
Returns the 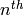 root of self.
root of self.
INPUT:
OUTPUT: an real or complex double
The output is complex if self is negative and n is even.
EXAMPLES:
sage: r = RDF(-125.0); r.nth_root(3)
-5.0
sage: r.nth_root(5)
-2.6265278044
sage: RDF(-2).nth_root(5)^5
-2.0
sage: RDF(-1).nth_root(5)^5
-1.0
sage: RDF(3).nth_root(10)^10
3.0
sage: RDF(-1).nth_root(2)
6.12323399574e-17 + 1.0*I
sage: RDF(-1).nth_root(4)
0.707106781187 + 0.707106781187*I
Return the real double field, which is the parent of self.
EXAMPLES:
sage: a = RDF(2.3)
sage: a.parent()
Real Double Field
sage: parent(a)
Real Double Field
Returns the precision of this number in bits.
Always returns 53.
EXAMPLES:
sage: RDF(0).prec()
53
Returns itself - we’re already real.
EXAMPLES:
sage: a = RDF(3)
sage: a.real()
3.0
Returns a number congruent to self mod 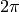 that lies in
the interval
that lies in
the interval ![(-\pi, \pi]](../../_images/math/e520a7aeab7e3c5078aebf7d07340c9485d2a110.png) .
.
Specifically, it is the unique ![x \in (-\pi, \pi]](../../_images/math/412081fe7c35b3471923f25e00406cda497cbd25.png) such
that `self = x + 2pi n` for some
such
that `self = x + 2pi n` for some
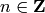 .
.
EXAMPLES:
sage: RDF(pi).restrict_angle()
3.14159265359
sage: RDF(pi + 1e-10).restrict_angle()
-3.14159265349
sage: RDF(1+10^10*pi).restrict_angle()
0.9999977606...
Given real number x, rounds up if fractional part is greater than .5, rounds down if fractional part is less than .5.
EXAMPLES:
sage: RDF(0.49).round()
0
sage: a=RDF(0.51).round(); a
1
This function returns the hyperbolic secant.
EXAMPLES:
sage: RDF(pi).sech()
0.0862667383341
sage: CDF(pi).sech()
0.0862667383341
Returns -1,0, or 1 if self is negative, zero, or positive; respectively.
EXAMPLES:
sage: RDF(-1.5).sign()
-1
sage: RDF(0).sign()
0
sage: RDF(2.5).sign()
1
Return the sign, mantissa, and exponent of self.
In Sage (as in MPFR), floating-point numbers of precision  are of the form
are of the form 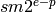 , where
, where 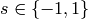 ,
,
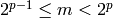 , and
, and 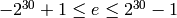 ; plus the special values +0, -0, +infinity,
-infinity, and NaN (which stands for Not-a-Number).
; plus the special values +0, -0, +infinity,
-infinity, and NaN (which stands for Not-a-Number).
This function returns s, m, and e-p. For the special values:
- ``+0`` returns (1, 0, 0)
- ``-0`` returns (-1, 0, 0)
- the return values for ``+infinity``, ``-infinity``, and
``NaN`` are not specified.
EXAMPLES::
sage: a=RDF(exp(1.0)); a
2.71828182846
sage: sign,mantissa,exponent=RDF(exp(1.0)).sign_mantissa_exponent()
sage: sign,mantissa,exponent
(1, 6121026514868073, -51)
sage: sign*mantissa*(2**exponent)==a
True
TESTS::
sage: RDF('+0').sign_mantissa_exponent()
(1, 0, 0)
sage: RDF('-0').sign_mantissa_exponent()
(-1, 0, 0)
Returns the sine of this number
EXAMPLES:
sage: RDF(2).sin()
0.909297426826
Returns a pair consisting of the sine and cosine.
EXAMPLES:
sage: t = RDF.pi()/6
sage: t.sincos()
(0.5, 0.866025403784)
Returns the hyperbolic sine of this number
EXAMPLES:
sage: q = RDF.pi()/12
sage: q.sinh()
0.264800227602
The square root function.
INPUT:
EXAMPLES:
sage: r = RDF(4.0)
sage: r.sqrt()
2.0
sage: r.sqrt()^2 == r
True
sage: r = RDF(4344)
sage: r.sqrt()
65.9090282131
sage: r.sqrt()^2 - r
0.0
sage: r = RDF(-2.0)
sage: r.sqrt()
1.41421356237*I
sage: RDF(2).sqrt(all=True)
[1.41421356237, -1.41421356237]
sage: RDF(0).sqrt(all=True)
[0.0]
sage: RDF(-2).sqrt(all=True)
[1.41421356237*I, -1.41421356237*I]
Return string representation of self.
EXAMPLES:
sage: a = RDF('4.5'); a.str()
'4.5'
sage: a = RDF('49203480923840.2923904823048'); a.str()
'4.92034809238e+13'
sage: a = RDF(1)/RDF(0); a.str()
'+infinity'
sage: a = -RDF(1)/RDF(0); a.str()
'-infinity'
sage: a = RDF(0)/RDF(0); a.str()
'NaN'
We verify consistency with RR (mpfr reals):
sage: str(RR(RDF(1)/RDF(0))) == str(RDF(1)/RDF(0))
True
sage: str(RR(-RDF(1)/RDF(0))) == str(-RDF(1)/RDF(0))
True
sage: str(RR(RDF(0)/RDF(0))) == str(RDF(0)/RDF(0))
True
Returns the tangent of this number
EXAMPLES:
sage: q = RDF.pi()/3
sage: q.tan()
1.73205080757
sage: q = RDF.pi()/6
sage: q.tan()
0.57735026919
Returns the hyperbolic tangent of this number
EXAMPLES:
sage: q = RDF.pi()/12
sage: q.tanh()
0.255977789246
Truncates this number (returns integer part).
EXAMPLES:
sage: RDF(2.99).trunc()
2
sage: RDF(-2.00).trunc()
-2
sage: RDF(0.00).trunc()
0
Returns the unit of least precision of self, which is the weight of the least significant bit of self. Unless self is exactly a power of two, it is gap between this number and the next closest distinct number that can be represented.
EXAMPLES:
sage: a = RDF(1)
sage: a - a.ulp() == a
False
sage: a - a.ulp()/2 == a
True
sage: a = RDF.pi()
sage: b = a + a.ulp()
sage: (a+b)/2 in [a,b]
True
sage: a = RDF(1)/RDF(0); a
+infinity
sage: a.ulp()
+infinity
sage: (-a).ulp()
+infinity
sage: a = RR('nan')
sage: a.ulp() is a
True
Return the Riemann zeta function evaluated at this real number.
Note
PARI is vastly more efficient at computing the Riemann zeta function. See the example below for how to use it.
EXAMPLES:
sage: RDF(2).zeta()
1.64493406685
sage: RDF.pi()^2/6
1.64493406685
sage: RDF(-2).zeta() # slightly random-ish arch dependent output
-2.37378795339e-18
sage: RDF(1).zeta()
+infinity
Return the unique instance of the Real Double Field.
EXAMPLES:
sage: RealDoubleField() is RealDoubleField()
True
Bases: sage.rings.ring.Field
An approximation to the field of real numbers using double precision floating point numbers. Answers derived from calculations in this approximation may differ from what they would be if those calculations were performed in the true field of real numbers. This is due to the rounding errors inherent to finite precision calculations.
EXAMPLES:
sage: RR == RDF
False
sage: RDF == RealDoubleField() # RDF is the shorthand
True
sage: RDF(1)
1.0
sage: RDF(2/3)
0.666666666667
A TypeError is raised if the coercion doesn’t make sense:
sage: RDF(QQ['x'].0)
...
TypeError: cannot coerce nonconstant polynomial to float
sage: RDF(QQ['x'](3))
3.0
One can convert back and forth between double precision real numbers and higher-precision ones, though of course there may be loss of precision:
sage: a = RealField(200)(2).sqrt(); a
1.4142135623730950488016887242096980785696718753769480731767
sage: b = RDF(a); b
1.41421356237
sage: a.parent()(b)
1.4142135623730951454746218587388284504413604736328125000000
sage: a.parent()(b) == b
True
sage: b == RR(a)
True
EXAMPLES:
sage: RDF.NaN()
NaN
Returns the algebraic closure of self, ie, the complex double field.
EXAMPLES:
sage: RDF.algebraic_closure()
Complex Double Field
Returns 0, since the field of real numbers has characteristic 0.
EXAMPLES:
sage: RDF.characteristic()
0
Returns the complex field with the same precision as self, ie, the complex double field.
EXAMPLES:
sage: RDF.complex_field()
Complex Double Field
Returns the functorial construction of self, namely, completion of
the rational numbers with respect to the prime at
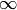 .
.
Also preserves other information that makes this field unique (i.e. the Real Double Field).
EXAMPLES:
sage: c, S = RDF.construction(); S
Rational Field
sage: RDF == c(S)
True
Returns Euler’s gamma constant to double precision
EXAMPLES:
sage: RDF.euler_constant()
0.577215664902
Return the factorial of the integer n as a real number.
EXAMPLES:
sage: RDF.factorial(100)
9.33262154439e+157
Return the generator of the real double field.
EXAMPLES:
sage: RDF.0
1.0
sage: RDF.gens()
(1.0,)
Returns True, to signify that elements of this field print without sums, so parenthesis aren’t required, e.g., in coefficients of polynomials.
EXAMPLES:
sage: RDF.is_atomic_repr()
True
Returns False, because doubles are not exact.
EXAMPLE:
sage: RDF.is_exact()
False
Returns False, since the field of real numbers is not finite. Technical note: There exists an upper bound on the double representation.
EXAMPLES:
sage: RDF.is_finite()
False
Returns log(2) to the precision of this field.
EXAMPLES:
sage: RDF.log2()
0.69314718056
sage: RDF(2).log()
0.69314718056
EXAMPLES:
sage: RDF.nan()
NaN
Returns pi to double-precision.
EXAMPLES:
sage: RDF.pi()
3.14159265359
sage: RDF.pi().sqrt()/2
0.886226925453
Return the precision of this real double field in bits.
Always returns 53.
EXAMPLES:
sage: RDF.prec()
53
Return the precision of this real double field in bits.
Always returns 53.
EXAMPLES:
sage: RDF.prec()
53
Return a random element of this real double field in the interval [min, max].
EXAMPLES:
sage: RDF.random_element()
0.736945423566
sage: RDF.random_element(min=100, max=110)
102.815947352
Returns the real field to the specified precision. As doubles have fixed precision, this will only return a real double field if prec is exactly 53.
EXAMPLES:
sage: RDF.to_prec(52)
Real Field with 52 bits of precision
sage: RDF.to_prec(53)
Real Double Field
Return an  -th root of unity in the real field, if one
exists, or raise a ValueError otherwise.
-th root of unity in the real field, if one
exists, or raise a ValueError otherwise.
EXAMPLES:
sage: RDF.zeta()
-1.0
sage: RDF.zeta(1)
1.0
sage: RDF.zeta(5)
...
ValueError: No 5th root of unity in self
Returns True if x is the field of real double precision numbers.
EXAMPLE:
sage: from sage.rings.real_double import is_RealDoubleField
sage: is_RealDoubleField(RDF)
True
sage: is_RealDoubleField(RealField(53))
False