AUTHORS:
TESTS:
sage: a = -2/3
sage: a == loads(dumps(a))
True
Bases: sage.categories.map.Map
TESTS:
sage: type(ZZ.convert_map_from(QQ))
<type 'sage.rings.rational.Q_to_Z'>
EXAMPLES:
sage: sage.rings.rational.Q_to_Z(QQ, ZZ).section()
Natural morphism:
From: Integer Ring
To: Rational Field
Bases: sage.structure.element.FieldElement
A Rational number.
Rational numbers are implemented using the GMP C library.
EXAMPLES:
sage: a = -2/3
sage: type(a)
<type 'sage.rings.rational.Rational'>
sage: parent(a)
Rational Field
sage: Rational('1/0')
...
TypeError: unable to convert 1/0 to a rational
sage: Rational(1.5)
3/2
sage: Rational('9/6')
3/2
sage: Rational((2^99,2^100))
1/2
sage: Rational(("2", "10"), 16)
1/8
sage: Rational(QQbar(125/8).nth_root(3))
5/2
sage: Rational(AA(209735/343 - 17910/49*golden_ratio).nth_root(3) + 3*AA(golden_ratio))
53/7
sage: QQ(float(1.5))
3/2
sage: QQ(RDF(1.2))
6/5
Conversion from PARI:
sage: Rational(pari('-939082/3992923'))
-939082/3992923
Return the additive order of self.
OUTPUT: integer or infinity
EXAMPLES:
sage: QQ(0).additive_order()
1
sage: QQ(1).additive_order()
+Infinity
Return the ceiling of this rational number.
OUTPUT: Integer
If this rational number is an integer, this returns this number, otherwise it returns the floor of this number +1.
EXAMPLES:
sage: n = 5/3; n.ceil()
2
sage: n = -17/19; n.ceil()
0
sage: n = -7/2; n.ceil()
-3
sage: n = 7/2; n.ceil()
4
sage: n = 10/2; n.ceil()
5
Return the characteristic polynomial of this rational number. This will always be just var - self; this is really here so that code written for number fields won’t crash when applied to rational numbers.
INPUT:
OUTPUT: Polynomial
EXAMPLES:
sage: (1/3).charpoly('x')
x - 1/3
AUTHORS:
Return the complex conjugate of this rational number, which is the number itself.
EXAMPLES:
sage: n = 23/11
sage: n.conjugate()
23/11
Return the content of self and other, i.e. the unique positive rational number c such that self/c and other/c are coprime integers.
other can be a rational number or a list of rational numbers.
EXAMPLES:
sage: a = 2/3
sage: a.content(2/3)
2/3
sage: a.content(1/5)
1/15
sage: a.content([2/5, 4/9])
2/45
Returns the denominator of this rational number.
EXAMPLES:
sage: x = 5/13
sage: x.denom()
13
sage: x = -9/3
sage: x.denom()
1
Returns the denominator of this rational number.
EXAMPLES:
sage: x = -5/11
sage: x.denominator()
11
sage: x = 9/3
sage: x.denominator()
1
Return the factorization of this rational number.
OUTPUT: Factorization
EXAMPLES:
sage: (-4/17).factor()
-1 * 2^2 * 17^-1
Trying to factor 0 gives an arithmetic error:
sage: (0/1).factor()
...
ArithmeticError: Prime factorization of 0 not defined.
Return the floor of this rational number as an integer.
OUTPUT: Integer
EXAMPLES:
sage: n = 5/3; n.floor()
1
sage: n = -17/19; n.floor()
-1
sage: n = -7/2; n.floor()
-4
sage: n = 7/2; n.floor()
3
sage: n = 10/2; n.floor()
5
Return the gamma function evaluated at self. This value is exact for integers and half-integers, and returns a symbolic value otherwise. For a numerical approximation, use keyword prec.
EXAMPLES:
sage: gamma(1/2)
sqrt(pi)
sage: gamma(7/2)
15/8*sqrt(pi)
sage: gamma(-3/2)
4/3*sqrt(pi)
sage: gamma(6/1)
120
sage: gamma(1/3)
gamma(1/3)
This function accepts an optional precision argument:
sage: (1/3).gamma(prec=100)
2.6789385347077476336556929410
sage: (1/2).gamma(prec=100)
1.7724538509055160272981674833
Return a gcd of the rational numbers self and other.
If self = other = 0, this is by convention 0. In all other cases it can (mathematically) be any nonzero rational number, but for simplicity we choose to always return 1.
EXAMPLES:
sage: gcd(1/3, 2/1)
1
sage: gcd(1/1, 0/1)
1
sage: gcd(0/1, 0/1)
0
Returns the absolute logarithmic height of this rational number.
INPUT:
OUTPUT:
(real) The absolute logarithmic height of this rational number.
ALGORITHM:
The height is the sum of the total archimedean and
non-archimedean components, which is equal to
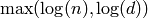 where
where 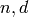 are the numerator and
denominator of the rational number.
are the numerator and
denominator of the rational number.
EXAMPLES:
sage: a = QQ(6/25)
sage: a.global_height_arch() + a.global_height_non_arch()
3.21887582486820
sage: a.global_height()
3.21887582486820
sage: (1/a).global_height()
3.21887582486820
sage: QQ(0).global_height()
0.000000000000000
sage: QQ(1).global_height()
0.000000000000000
Returns the total archimedean component of the height of this rational number.
INPUT:
OUTPUT:
(real) The total archimedean component of the height of this rational number.
ALGORITHM:
Since  has only one infinite place this is just the value
of the local height at that place. This separate function is
included for compatibility with number fields.
has only one infinite place this is just the value
of the local height at that place. This separate function is
included for compatibility with number fields.
EXAMPLES:
sage: a = QQ(6/25)
sage: a.global_height_arch()
0.000000000000000
sage: (1/a).global_height_arch()
1.42711635564015
sage: (1/a).global_height_arch(100)
1.4271163556401457483890413081
Returns the total non-archimedean component of the height of this rational number.
INPUT:
OUTPUT:
(real) The total non-archimedean component of the height of this rational number.
ALGORITHM:
This is the sum of the local heights at all primes  , which
may be computed without factorization as the log of the
denominator.
, which
may be computed without factorization as the log of the
denominator.
EXAMPLES:
sage: a = QQ(5/6)
sage: a.support()
[2, 3, 5]
sage: a.global_height_non_arch()
1.79175946922805
sage: [a.local_height(p) for p in a.support()]
[0.693147180559945, 1.09861228866811, 0.000000000000000]
sage: sum([a.local_height(p) for p in a.support()])
1.79175946922805
The max absolute value of the numerator and denominator of self, as an Integer.
OUTPUT: Integer
EXAMPLES:
sage: a = 2/3
sage: a.height()
3
sage: a = 34/3
sage: a.height()
34
sage: a = -97/4
sage: a.height()
97
AUTHORS:
Note
For the logarithmic height, use global_height().
Returns the imaginary part of self, which is zero.
EXAMPLES:
sage: (1/239).imag()
0
Determine if the rational number is S-integral.
x is S-integral if x.valuation(p)>=0 for all p not in S, i.e.,
the denominator of x is divisible only by the primes in  .
.
INPUT:
OUTPUT: bool
Note
Primality of the entries in  is not checked.
is not checked.
EXAMPLES:
sage: QQ(1/2).is_S_integral()
False
sage: QQ(1/2).is_S_integral([2])
True
sage: [a for a in range(1,11) if QQ(101/a).is_S_integral([2,5])]
[1, 2, 4, 5, 8, 10]
Determine if the rational number is an S-unit.
x is an S-unit if x.valuation(p)==0 for all p not in S, i.e.,
the numerator and denominator of x are divisible only by the
primes in  .
.
INPUT:
OUTPUT: bool
Note
Primality of the entries in  is not checked.
is not checked.
EXAMPLES:
sage: QQ(1/2).is_S_unit()
False
sage: QQ(1/2).is_S_unit([2])
True
sage: [a for a in range(1,11) if QQ(10/a).is_S_unit([2,5])]
[1, 2, 4, 5, 8, 10]
Determine if a rational number is integral (i.e is in
 ).
).
OUTPUT: bool
EXAMPLES:
sage: QQ(1/2).is_integral()
False
sage: QQ(4/4).is_integral()
True
Returns True if self is an nth power, else False.
INPUT:
Note
Use this function when you need to test if a rational number is an n’th power, but do not need to know the value of its n’th root. If the value is needed, use nth_root().
AUTHORS:
EXAMPLES:
sage: QQ(25/4).is_nth_power(2)
True
sage: QQ(125/8).is_nth_power(3)
True
sage: QQ(-125/8).is_nth_power(3)
True
sage: QQ(25/4).is_nth_power(-2)
True
sage: QQ(9/2).is_nth_power(2)
False
sage: QQ(-25).is_nth_power(2)
False
Determine if a rational number is one.
OUTPUT: bool
EXAMPLES:
sage: QQ(1/2).is_one()
False
sage: QQ(4/4).is_one()
True
Determines whether this rational number is a square in Q_p (or in R when p = infinity).
INPUT:
Returns True if self is a perfect power.
INPUT:
be a perfect power. This does not affect the correctness of the output, only the runtime.
If expected_value is False (default) it will check the smallest of the numerator and denominator is a perfect power as a first step, which is often faster than checking if the quotient is a perfect power.
EXAMPLES:
sage: (4/9).is_perfect_power()
True
sage: (144/1).is_perfect_power()
True
sage: (4/3).is_perfect_power()
False
sage: (2/27).is_perfect_power()
False
sage: (4/27).is_perfect_power()
False
sage: (-1/25).is_perfect_power()
False
sage: (-1/27).is_perfect_power()
True
sage: (0/1).is_perfect_power()
True
The second parameter does not change the result, but may change the runtime.
sage: (-1/27).is_perfect_power(True)
True
sage: (-1/25).is_perfect_power(True)
False
sage: (2/27).is_perfect_power(True)
False
sage: (144/1).is_perfect_power(True)
True
This test makes sure we workaround a bug in GMP (see trac #4612):
sage: [ -a for a in srange(100) if not QQ(-a^3).is_perfect_power() ]
[]
sage: [ -a for a in srange(100) if not QQ(-a^3).is_perfect_power(True) ]
[]
Return whether or not this rational number is a square.
OUTPUT: bool
EXAMPLES:
sage: x = 9/4
sage: x.is_square()
True
sage: x = (7/53)^100
sage: x.is_square()
True
sage: x = 4/3
sage: x.is_square()
False
sage: x = -1/4
sage: x.is_square()
False
Return the least common multiple of self and other.
One way to define this notion is the following:
Note that each rational positive rational number can be written as a product of primes with integer (positive or negative) powers in a unique way.
Then, the LCM of two rational numbers x,y can be defined by specifying that the exponent of every prime p in lcm(x,y) is the supremum of the exponents of p in x, and the exponent of p in y (The primes that does not appear in the decomposition of x or y are considered to have exponent zero).
This definition is consistent with the definition of the LCM in the rational integers. Our hopefully interesting notion of LCM for rational numbers is illustrated in the examples below.
EXAMPLES:
sage: lcm(2/3,1/5)
2
This is consistent with the definition above, since:
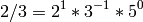
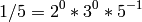
and hence,
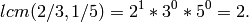
sage: lcm(2/3,7/5)
14
In this example:
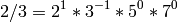
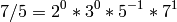
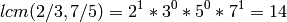
sage: lcm(1/3,1/5)
1
In this example:
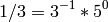
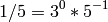
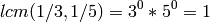
sage: lcm(1/3,1/6)
1/3
In this example:
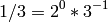
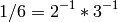
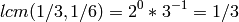
Return a list with the rational element in it, to be compatible with the method for number fields.
OUTPUT:
EXAMPLES:
sage: m = 5/3
sage: m.list()
[5/3]
Returns the local height of this rational number at the prime  .
.
INPUT:
OUTPUT:
(real) The local height of this rational number at the
prime  .
.
EXAMPLES:
sage: a = QQ(25/6)
sage: a.local_height(2)
0.693147180559945
sage: a.local_height(3)
1.09861228866811
sage: a.local_height(5)
0.000000000000000
Returns the Archimedean local height of this rational number at the infinite place.
INPUT:
OUTPUT:
(real) The local height of this rational number  at the
unique infinite place of
at the
unique infinite place of  , which is
, which is
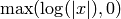 .
.
EXAMPLES:
sage: a = QQ(6/25)
sage: a.local_height_arch()
0.000000000000000
sage: (1/a).local_height_arch()
1.42711635564015
sage: (1/a).local_height_arch(100)
1.4271163556401457483890413081
Return the minimal polynomial of this rational number. This will always be just x - self; this is really here so that code written for number fields won’t crash when applied to rational numbers.
INPUT:
OUTPUT: Polynomial
EXAMPLES:
sage: (1/3).minpoly('x')
x - 1/3
AUTHORS:
Return the remainder upon division of self by the unsigned long integer n.
INPUT:
OUTPUT: integer
EXAMPLES:
sage: (-4/17).mod_ui(3)
1
sage: (-4/17).mod_ui(17)
...
ArithmeticError: The inverse of 0 modulo 17 is not defined.
Return the multiplicative order of self.
OUTPUT: Integer or infinity
EXAMPLES:
sage: QQ(1).multiplicative_order()
1
sage: QQ('1/-1').multiplicative_order()
2
sage: QQ(0).multiplicative_order()
+Infinity
sage: QQ('2/3').multiplicative_order()
+Infinity
sage: QQ('1/2').multiplicative_order()
+Infinity
Returns the norm from Q to Q of x (which is just x). This was added for compatibility with NumberFields.
OUTPUT:
EXAMPLES:
sage: (1/3).norm()
1/3
AUTHORS:
Computes the nth root of self, or raises a ValueError if self is not a perfect nth power.
INPUT:
AUTHORS:
EXAMPLES:
sage: (25/4).nth_root(2)
5/2
sage: (125/8).nth_root(3)
5/2
sage: (-125/8).nth_root(3)
-5/2
sage: (25/4).nth_root(-2)
2/5
sage: (9/2).nth_root(2)
...
ValueError: not a perfect 2nd power
sage: (-25/4).nth_root(2)
...
ValueError: cannot take even root of negative number
Return the numerator of this rational number.
EXAMPLE:
sage: x = -5/11
sage: x.numer()
-5
Return the numerator of this rational number.
EXAMPLE:
sage: x = 5/11
sage: x.numerator()
5
sage: x = 9/3
sage: x.numerator()
3
Return the period of the repeating part of the decimal expansion of this rational number.
ALGORITHM: When a rational number 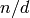 with
with 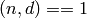 is
expanded, the period begins after
is
expanded, the period begins after  terms and has length
terms and has length
 , where
, where  and
and  are the smallest numbers satisfying
are the smallest numbers satisfying
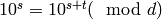 . In general if
. In general if 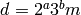 where
where  is coprime to 10, then
is coprime to 10, then 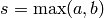 and
and  is the order of
10 modulo
is the order of
10 modulo  .
.
EXAMPLES:
sage: (1/7).period()
6
sage: RR(1/7)
0.142857142857143
sage: (1/8).period()
1
sage: RR(1/8)
0.125000000000000
sage: RR(1/6)
0.166666666666667
sage: (1/6).period()
1
sage: x = 333/106
sage: x.period()
13
sage: RealField(200)(x)
3.1415094339622641509433962264150943396226415094339622641509
Returns self with all powers of all primes in S removed.
INPUT:
OUTPUT: rational
Note
Primality of the entries in  is not checked.
is not checked.
EXAMPLES:
sage: QQ(3/4).prime_to_S_part()
3/4
sage: QQ(3/4).prime_to_S_part([2])
3
sage: QQ(-3/4).prime_to_S_part([3])
-1/4
sage: QQ(700/99).prime_to_S_part([2,3,5])
7/11
sage: QQ(-700/99).prime_to_S_part([2,3,5])
-7/11
sage: QQ(0).prime_to_S_part([2,3,5])
0
sage: QQ(-700/99).prime_to_S_part([])
-700/99
Returns the real part of self, which is self.
EXAMPLES:
sage: (1/2).real()
1/2
Returns the nearest integer to self, rounding away from 0 by default, for consistency with the builtin Python round.
INPUT:
OUTPUT: Integer
EXAMPLES:
sage: (9/2).round()
5
sage: n = 4/3; n.round()
1
sage: n = -17/4; n.round()
-4
sage: n = -5/2; n.round()
-3
sage: n.round("away")
-3
sage: n.round("up")
-2
sage: n.round("down")
-3
sage: n.round("even")
-2
sage: n.round("odd")
-3
The square root function.
INPUT:
EXAMPLES:
sage: x = 25/9
sage: x.sqrt()
5/3
sage: sqrt(x)
5/3
sage: x = 64/4
sage: x.sqrt()
4
sage: x = 100/1
sage: x.sqrt()
10
sage: x.sqrt(all=True)
[10, -10]
sage: x = 81/5
sage: x.sqrt()
9*sqrt(1/5)
sage: x = -81/3
sage: x.sqrt()
3*sqrt(-3)
sage: n = 2/3
sage: n.sqrt()
sqrt(2/3)
sage: n.sqrt(prec=10)
0.82
sage: n.sqrt(prec=100)
0.81649658092772603273242802490
sage: n.sqrt(prec=100)^2
0.66666666666666666666666666667
sage: n.sqrt(prec=53, all=True)
[0.816496580927726, -0.816496580927726]
sage: n.sqrt(extend=False, all=True)
...
ValueError: square root of 2/3 not a rational number
sage: sqrt(-2/3, all=True)
[sqrt(-2/3), -sqrt(-2/3)]
sage: sqrt(-2/3, prec=53)
0.816496580927726*I
sage: sqrt(-2/3, prec=53, all=True)
[0.816496580927726*I, -0.816496580927726*I]
AUTHORS:
Return numerical approximation with given number of bits of precision to this rational number. If all is given, return both approximations.
INPUT:
EXAMPLES:
sage: (5/3).sqrt_approx()
doctest:1172: DeprecationWarning: This function is deprecated. Use sqrt with a given number of bits of precision instead.
1.29099444873581
sage: (990829038092384908234098239048230984/4).sqrt_approx()
4.9770197862083713747374920870362581922510725585130996993055116540856385e17
sage: (5/3).sqrt_approx(prec=200)
1.2909944487358056283930884665941332036109739017638636088625
sage: (9/4).sqrt_approx()
3/2
Return the square free part of  , i.e., an integer z such
that
, i.e., an integer z such
that 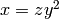 , for a perfect square
, for a perfect square 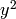 .
.
EXAMPLES:
sage: a = 1/2
sage: a.squarefree_part()
2
sage: b = a/a.squarefree_part()
sage: b, b.is_square()
(1/4, True)
sage: a = 24/5
sage: a.squarefree_part()
30
INPUT:
OUTPUT: string
EXAMPLES:
sage: (-4/17).str()
'-4/17'
sage: (-4/17).str(2)
'-100/10001'
Note that the base must be at most 36.
sage: (-4/17).str(40)
...
ValueError: base (=40) must be between 2 and 36
sage: (-4/17).str(1)
...
ValueError: base (=1) must be between 2 and 36
Return a sorted list of the primes where this rational number has non-zero valuation.
OUTPUT: The set of primes appearing in the factorization of this rational with nonzero exponent, as a sorted list.
EXAMPLES:
sage: (-4/17).support()
[2, 17]
Trying to find the support of 0 gives an arithmetic error:
sage: (0/1).support()
...
ArithmeticError: Support of 0 not defined.
Returns the trace from Q to Q of x (which is just x). This was added for compatibility with NumberFields.
OUTPUT:
EXAMPLES:
sage: (1/3).trace()
1/3
AUTHORS:
Returns a pair: the p-adic valuation of self, and the p-adic unit of self, as a Rational.
We do not require the p be prime, but it must be at least 2. For more documentation see Integer.val_unit
INPUT:
OUTPUT:
EXAMPLES:
sage: (-4/17).val_unit(2)
(2, -1/17)
sage: (-4/17).val_unit(17)
(-1, -4)
sage: (0/1).val_unit(17)
(+Infinity, 1)
AUTHORS:
Return the power of p in the factorization of self.
INPUT:
OUTPUT:
(integer or infinity) Infinity if self is zero, otherwise the
(positive or negative) integer  such that self =
such that self = 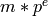 with
with  coprime to
coprime to  .
.
Note
See also val_unit() which returns the pair 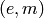 .
.
EXAMPLES:
sage: x = -5/9
sage: x.valuation(5)
1
sage: x.valuation(3)
-2
sage: x.valuation(2)
0
Some edge cases:
sage: (0/1).valuation(4)
+Infinity
sage: (7/16).valuation(4)
-2
Bases: sage.categories.morphism.Morphism
EXAMPLES:
sage: QQ.coerce_map_from(ZZ).section()
Generic map:
From: Rational Field
To: Integer Ring
Compute 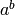 as an integer, if it is integral, or return None.
The positive real root is taken for even denominators.
as an integer, if it is integral, or return None.
The positive real root is taken for even denominators.
INPUT:
a -- an Integer
b -- a positive Rational
OUTPUT:
`a^b` as an Integer or None
EXAMPLES:
sage: from sage.rings.rational import integer_rational_power
sage: integer_rational_power(49, 1/2)
7
sage: integer_rational_power(27, 1/3)
3
sage: integer_rational_power(-27, 1/3) is None
True
sage: integer_rational_power(-27, 2/3) is None
True
sage: integer_rational_power(512, 7/9)
128
sage: integer_rational_power(27, 1/4) is None
True
sage: integer_rational_power(-16, 1/4) is None
True
sage: integer_rational_power(0, 7/9)
0
sage: integer_rational_power(1, 7/9)
1
sage: integer_rational_power(-1, 7/9) is None
True
sage: integer_rational_power(-1, 8/9) is None
True
sage: integer_rational_power(-1, 9/8) is None
True
Make a rational number from s (a string in base 32)
INPUT:
OUTPUT: Rational
EXAMPLES:
sage: (-7/15).str(32)
'-7/f'
sage: sage.rings.rational.make_rational('-7/f')
-7/15
Find the rational reconstruction of a mod m, if it exists.
INPUT:
OUTPUT:
EXAMPLES:
sage: Integers(100)(2/3)
34
sage: sage.rings.rational.pyrex_rational_reconstruction(34, 100)
2/3
Compute rationals or integers  and
and  such that
such that 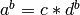 with
with  small. This is used for simplifying radicals.
small. This is used for simplifying radicals.
INPUT:
a -- a Rational or Integer
b -- a Rational
factor_limit -- the limit used in factoring a
EXAMPLES:
sage: from sage.rings.rational import rational_power_parts
sage: rational_power_parts(27, 1/2)
(3, 3)
sage: rational_power_parts(-128, 3/4)
(8, -8)
sage: rational_power_parts(-4, 1/2)
(2, -1)
sage: rational_power_parts(-4, 1/3)
(1, -4)
sage: rational_power_parts(9/1000, 1/2)
(3/10, 1/10)
TESTS:
Check if #8540 is fixed:
sage: rational_power_parts(3/4, -1/2)
(2, 3)
sage: t = (3/4)^(-1/2); t
2/3*sqrt(3)
sage: t^2
4/3